基于风电消纳电热储能装置热流固耦合研究
张雪平,齐凤升,邢作霞,单建标,李宝宽
(1东北大学冶金学院,辽宁 沈阳 110819;2沈阳工业大学,辽宁 沈阳 110870)
风能由于其具有分布地区广泛、不造成环境污染、资源蕴藏量丰富等优势,现已成为可再生能源发展的主力军。然而,截至目前风电的发展还有诸多问题有待解决,如风电并网、消纳问题[1]依然严重,尤其是在三北地区,弃风现象较为普遍。我国电力系统负荷谷峰比例达0.4[2]以上,电力谷峰问题较为突出。在供暖地区,电蓄热技术是解决风电并网问题,提高电网调峰能力[3]的有效途径之一。系统利用低谷时期的电能或者无法并网消纳的弃风电通过电加热装置将热量储存于蓄热材料中,当需要时对热用户进行供热。
国内外针对固体电蓄热技术做了大量研究,尤其是在蓄热体经济性分析、蓄热材料的选择以及影响蓄热性能因素等方面进行分析[4-5]。KHARE等[6]对多种高温固体电蓄热材料进行了物性参数和经济性分析,发现镁砖以及高铝混凝土成本最低、热容量较高。哈尔滨工业大学的廖晋[7]深入研究了固体电蓄热技术理论及其装置的热工特性,提出了利用固体电蓄热装置消纳过剩风电的方法。胡思科、周林林等[8]将蓄热体模型简化为二维模型,分析了放热孔形及孔数对蓄放热特性的影响,给定蓄热体固体材料温度作为放热热源,研究结果为蓄热设备的涉及提供一定的参考依据。以往针对蓄热装置蓄放热过程的研究运用的方法或者将蓄热体简化,选取其中包含单个换热通孔进行二维模拟,或者通过运用传热学知识计算得到蓄热材料与换热介质边界处(空气、水等)热流密度,将流固边界设为热流边界条件。两种方法只能简单说明蓄热体温度场的变化规律,建立的传热模型与实际相差加大,不能全面的说明问题。装置内传热过程较为复杂,涉及辐射、对流以及导热传热,且涉及固体区域与流体区域的传热耦合,蓄热体周期性地蓄热和释热,温度分布不均匀,企业投入运行的蓄热装置易出现开裂、坍塌等问题影响装置工作。本文在上述研究的基础上,对某企业运行中的固体电蓄热装置建立了流固耦合装置内热流固多场三维耦合传热数学模型,采用流固耦合传热的整场求解法[9],详细分析了装置内蓄热材料的温度场及应变场,并在此基础上对比了三种不同孔隙率、电热丝排布方式对蓄热装置温度分布均匀性的影响。
1 模 型
本文研究的固体电蓄热装置可用于弃风电消纳与电力调峰系统中。装置主要部件有蓄热体、电热丝、换热管、循环风机等。蓄热时,无法并网消纳的风电通过加热丝以辐射换热的方式将电能转换成热量储存于蓄热体中;释热时,冷空气流过通道与蓄热材料表面直接接触,蓄热体蓄存的热量通过对流换热的方式将空气加热,被加热的空气通过热交换器将热量转移给热用户。装置工作原理示意图如图1所示。本文仅研究蓄热过程。

图1 固体电蓄热装置工作原理示意图Fig.1 Schematic diagram of working principle of solid electric heat storage device
1.1 几何及网格模型
整个蓄热体组件由2028块氧化镁砖堆砌而成,砖型为异型砖,蓄热体的总体积为8.355m3。蓄热体内流体通道数为78个,其中36个通道内布置电热丝,孔隙率为15%(保持蓄热总体积不变,改变通道尺寸,通道总截面积与装置截面积之比定义为孔隙率)。为了确定影响研究对象运行特性的主要因素,对研究模型进行合理简化:①蓄热材料的内部是均匀且连续填充的固态导热介质,蓄热单元看作一个长宽高固定的一个立体结构;②由于电热丝的横截面积相对于整个蓄热单元而言非常小,故将其看作棒热源处理。蓄热体长2300mm,宽1500mm,高1874mm。为了使流体全部流入流体通道,蓄热体上面以及两个侧面设有砖体挡板,用来阻挡绕流蓄热体外部的流体。固体电蓄热装置被分为6个区域,每个区域均布有热电偶监测温度,几何结构如图2所示。

图2 固体电蓄热装置结构图Fig.2 Structural chart of solid electric heat storage device

图3 固体电蓄热装置网格图Fig.3 Grid of solid electric heat storage device
系统工作时,流体流过通道与蓄热材料表面直接接触,传热方式为流-固耦合对流传热,在结构化网格划分的过程中,将流体区域和固体区域分离开来,流体区域与固体区域网格节点一一对应,数据通过流固耦合界面直接传递。考虑计算速度时间因素,确定网格数为106万,如图3所示。
1.2 控制方程
在整个装置内,共存在三种不同形式的传热过程,即电热丝与蓄热砖的辐射换热,蓄热砖内部的导热以及蓄热砖与空气的流固耦合对流换热。经计算确定,空气在通道内流动属于湍流流动,近壁面处,采用壁面函数法[10]处理边界层流动,湍流模型选用标准κ-ε湍流模型[11]。DO辐射模型[12]考虑了所有光学深度区间的辐射,且占用计算机内存适中,本文辐射模型选用DO辐射模型。流体区域、固体区域以及界面处控制方程如下。
(1)流体区域控制方程质量守恒方程

能量守恒方程
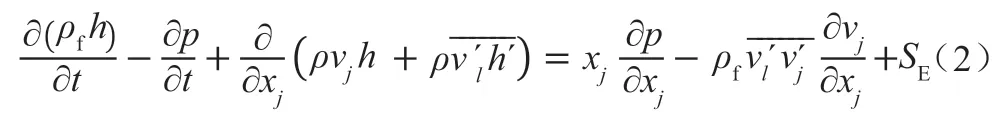
动量守恒方程
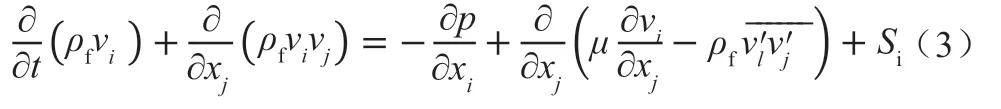
其中,ρf为流体密度,v为流体时均速度,v'为脉动速度,h为流体焓,p为流体的静压,μ为湍流黏度,SE、Si分别为能量源项以及动量源项,在本研究中为0。
(2)固体区域只有热量传递过程,其导热微分控制方程

其中,ρ为密度,τ为时间,λ为导热系数,c为比热容,Ts为固体温度,Φ为固体内部体积热源。
(3)流固交界面上满足能量连续性条件,即温度、热流密度、位移相等。热流密度控制方程式为

其中,qf、qs分别为流-固交界面上流体侧和固体侧的热流密度,k为对流换热系数,Tf为靠近交界面处流体温度,Tm为交界面处温度,n为流-固交界面法向量。
1.3 应变/应力理论
物质被加热或冷却时会产生热胀冷缩,即发生“热变形”,变形量和材料的膨胀系数有关。而由于存在约束,热变形不能自由发生。这种因温度变化而产生的应力称之为热应力。对蓄热体作热应力应变分析计算遵循材料力学的热弹性理论。应变与节点位移矢量关系方程为
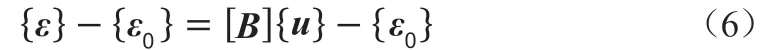
应力应变关系方程
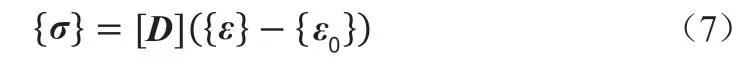
式中,{σ}为应力矢量,[D]为弹性矩阵,{ε}为总应变矢量,{ε0}为热应变矢量,[B]为节点应变-位移矩阵,{u}为节点位移矢量。
由式(6)~(7)可得:

热应变矢量方程为
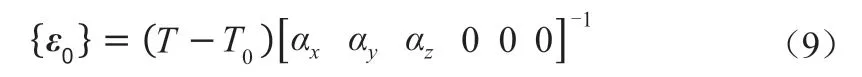
其中,T为单元体当前温度(K),T0为初始温度(K),αx、αy、αz分别为三个方向的热膨胀系数(1/K)。考虑到蓄热砖体在其温度变化范围内热膨胀系数变化较小,在计算时将其设为一常值。式(9)可简化为
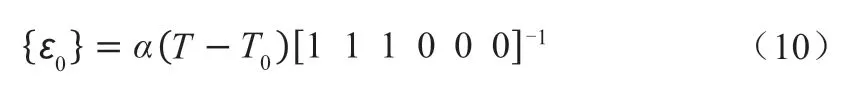
则应变总矢量为

引起蓄热体材料产生变形的原因主要有两个,温度分布不均以及流场对材料界面处的压强。根据式(11)联立平衡方程、几何方程即可求解出对应的热变形以及热应力。
1.4 均匀性评价指标
基于不同工况下蓄热装置温度场分布规律相似,采用相对标准偏差指标[13]衡量温度场的均匀程度,其计算公式为
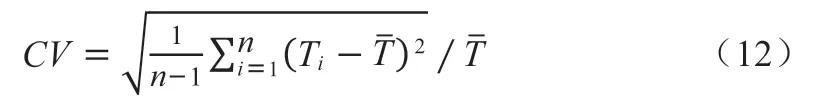
式中,CV为相对标准偏差,取0~1,越接近0表示温度均匀性越好,n为数据点个数,Ti为某点温度值,为数据平均值。
1.5 边界条件和计算方法
边界条件根据装置实际运行过程中操作数据给出。蓄热时,加热丝总功率为270 kW,为了防止加热丝表面过热以及风机不断启停对设备影响,向装置内通入少量空气。入口为速度入口,空气流速为0.01 m/s,温度根据现场实际测试温度编译UDF导入确定。出口设为压力出口,壁面设为绝热无滑移边界条件。流体与固体表面的交界处设为耦合壁面。初始蓄热体内温度均匀为482 K,总蓄热时间为24000 s。氧化镁砖热物理性质如表1所示。

表1 氧化镁砖的热物理性质Table1 The thermal physical properties of magnesia brick
2 模拟结果与讨论
2.1 模型验证
为了验证所建三维模型的正确性,提取6个热电偶处的计算温度与监测进行对比,如图4所示。模拟初始条件根据企业提供的数据设置,6个热电偶初始温度有所不同,取装置内平均温度作为模拟初始温度。误差产生的来源主要是初始温度的不同,热电偶测得的温度为局部区域温度,而计算初始化取装置内平均温度为482 K。4号热电偶的初始温度为442 K,与装置初始平均温度最为接近,计算过程中最大为8%。各点的实验温度与计算温度的变化趋势基本一致,温度上升速率也差别不大。
2.2 温度场及应变场分析
图5为蓄热体在加热过程中不同时间段(7200s、14400s、21600s以及24000s)温度云图(z=0.15m)。可以看出,随着蓄热过程的进行,布置加热丝的通道表面由于直接接受电热丝辐射,温度最先升高,周围砖体通过导热传热,温度逐渐降低,传热速率主要取决于蓄热材料的导热系数以及传热温差。布置加热丝的通道表面温度最高可达932K,上部隔板处温度上升较慢,无明显升高。
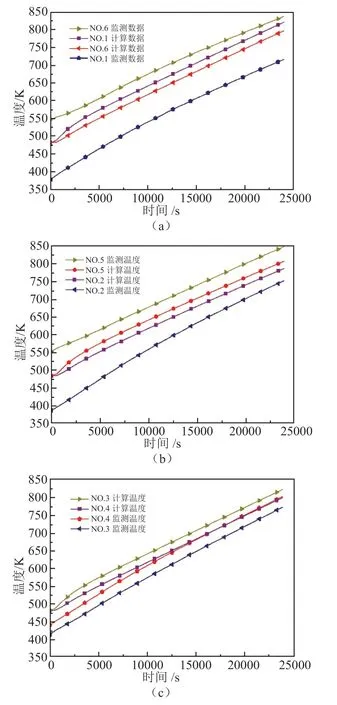
图4 计算值与现场数据对比Fig.4 Comparison between calculated values and measurement date
将模拟得到的固体温度导入到Workbench热应力分析模块,将装置底部以及四周设置为固定约束,利用等效应力以及总膨胀量得到变形、应力云图分布如图6、图7所示。蓄热体受热向四周膨胀,加上底部约束,从下端到上端,热膨胀量量呈抛物线型分布,中部中心区域热膨胀量量最大。约束部位蓄热体受热无法自由膨胀,产生的热应力最大,在这些区域砖体易出现断裂现象。图8给出了蓄热体平均温度以及膨胀量随时间变化的曲线。蓄热体平均温度以及最大膨胀量均随着时间呈线性上升。蓄热结束后,蓄热体平均温度达760K,最大膨胀量为0.015m,与蓄热体原宽相比,最大变形率最大为1%,影响可以忽略。
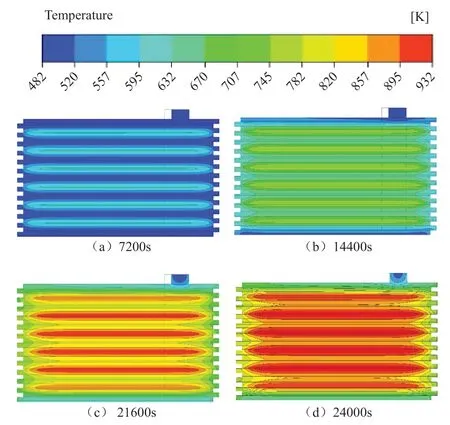
图5 蓄热体(z=0.15m截面)加热过程中温度分布Fig.5 Temperature distribution of heat storage (z=0.15m section) during heating process

图6 蓄热体变形量分布Fig.6 Distribution of deformation in heat storage

图7 蓄热体等效应力分布Fig.7 Distribution of equivalent stress
2.3 电热丝个数对蓄热温度均匀性影响
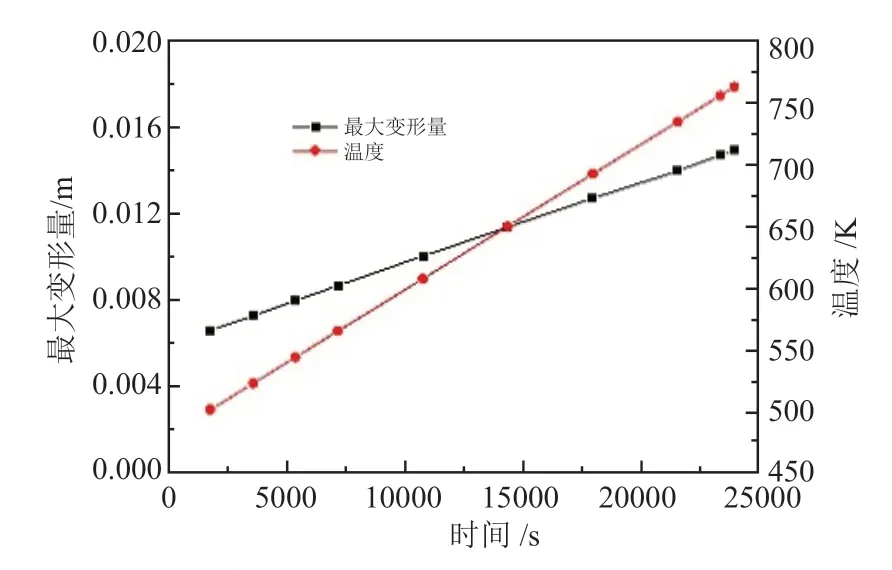
图8 蓄热体最大变形量、温度随时间变化曲线Fig.8 Distribution of deformation and maximum stress during heating process
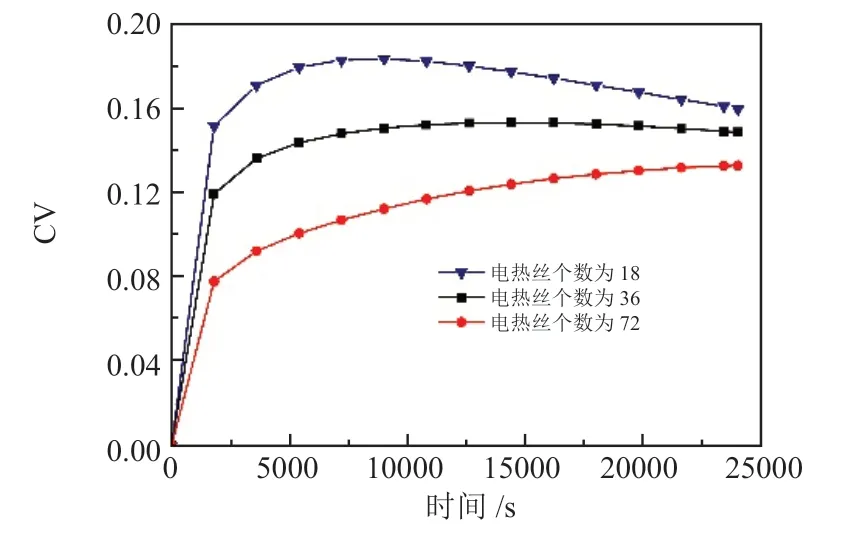
图9 相对标准偏差随时间变化曲线Fig.9 Curve of relative standard deviation during heating process
在蓄热过程中,电热丝的分布密度及单个功率对蓄热温度均匀性产生影响。根据傅里叶导热定律,热流量与温差成正比,而与距离成反比。当单个电热丝的功率不变时,电热丝分布密度越大,温度均匀性越好。当电热丝分布密度不变时,电热丝功率越大,则温度均匀性较差。在保持电热丝总加热功率不变情况下,合理选择电热丝的个数可获得较好蓄热温度均匀性。图9为不同电热丝个数下,相对标准偏差随时间的变化曲线。三种情况下,在蓄热初期,蓄热体内部温度梯度较大,相对标准偏差增大速度较快,后期电热丝为18的工况出现缓慢下降的现象,最终趋于不变。电热丝个数为72的工况下,蓄热体均匀性程度最大,个数为18的工况均匀性较弱。
为进一步明确电热丝个数对蓄热温度均匀性的影响,图10给出了同一截面下,蓄热体温度分布随电热丝个数变化的云图。电热丝个数为18的工况下,高温区与低温区区别明显,靠近电热丝周围的蓄热砖温度较高,而隔板处以及下部通道处,温度呈波峰波谷状分布,这是由于远离电热丝,蓄热体内部通过导热传播热量,而又受周围左右两个电热丝的影响,距离越远,低温区越大。随着电热丝个数增多,上部低温区面积变少,下部温度趋于均匀,最高温由1149K降为858K,最低温由524K升为565K。电热丝个数为72的工况下蓄热温度均匀性程度最好。
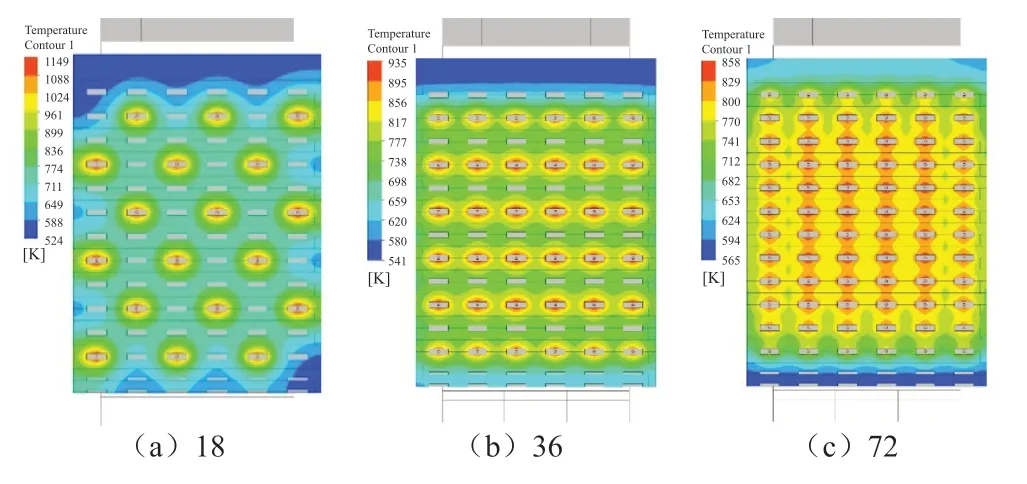
图10 不同电热丝个数在 同一截面处温度分布云图Fig.10 Temperature distribution at same section with number of electric heating wire (a) 18,(b) 36,(c) 72
2.4 孔隙率对蓄热温度均匀性影响
图11为不同孔隙率下,相对标准偏差随时间的变化。在蓄热初期(1800s内),电热丝温度与蓄热砖温度相差较大,辐射热流量较大,而蓄热体内部导热热流传播速率取决于材料的热扩散系数,导热需要一定的时间,蓄热体内部温度梯度较大,故相对标准偏差增长速度较快。大约加热7000s之后,三种工况下的标准偏差基本不再发生变化,孔隙率为20%的工况相对标准偏差有所降低。根据此评价指标,孔隙率为20%的工况蓄热温度均匀性较好,而15%的工况蓄热温度均匀性相对较差。
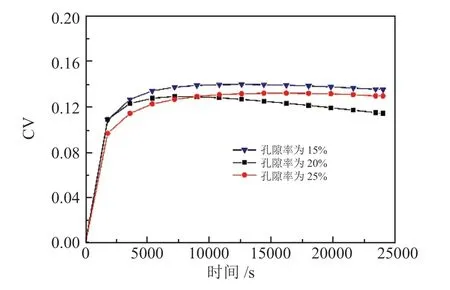
图11 相对标准偏差随时间变化曲线Fig.11 D Curve of relative standard deviation during heating process
图12所示为同一位置处,孔隙率为15%、20%以及25%的温度分布云图。孔隙率为25%的工况,其最高温与最低温相差最小,然而其低温区面积最大,整体来看,其内部温度梯度较大。孔隙率为20%的工况其最高温仅为914K,而其温度分布与15%的工况相似,温度分布均匀性较其他两个工况好。
3 结 论
文章以某企业实际运行的固体电蓄热装置为原型建立了三维流动与传热的数学模型,采用整场流固耦合法,将流固界面处难以确定的热流边界条件转化为内部边界,详细分析了装置蓄热过程中内部温度分布均匀性以及变形量,结论如下。
(1)将模拟结果与实验数据对比,误差产生的来源主要是初始温度的不同,各点的实验温度与计算温度的变化趋势基本一致,温度上升速率也差别不大。采用流固耦合传热模型较为精确。
(2)在蓄热的过程中,蓄热体平均温度近似呈线性上升,最终达760K左右,蓄热量为蓄热体最大膨胀量为0.015m,最大应力出现在挡板处,与蓄热体原宽相比,最大变形率最大为1%,影响可以忽略。
(3)运用相对标准偏差评价蓄热温度均匀性,并结合温度云图,得到电热丝个数为72、孔隙率为20%的蓄热体温度分布均匀性较好,此结果为装置结构优化提供参考。

