考虑电价激励的孤岛微电网经济调度策略
郝文博,郑常宝,,胡存刚,,芮 涛,张 进
(1安徽大学电气工程与自动化学院,安徽 合肥 230031;2安徽大学工业节电与电能质量控制协同创新中心,安徽 合肥 230601)
微电网作为分布式电源的一种有效利用和管理方式,因其灵活、高效和可靠的优点近年来得到了广泛地应用[1-2]。由于可再生能源的出力存在很大的随机性和波动性,会影响微电网的供电可靠性与运行效益[3]。因此,研究如何协调微电网中各类分布式电源的功率输出以保证系统内部功率平衡,实现最优经济调度具有重要的意义。
文献[4]中指出微电网系统应进行需求侧管理,需求响应在微电网的优化调度中发挥着重要作用[5]。目前,需求响应通常被化分为基于价格的需求响应和基于激励的需求响应[6-8]。用户侧可以通过需求响应来调整自己的固有用电行为,这种方式让微电网系统更加稳定、经济、高效的运行。由于电能交易市场参与者的利益诉求不同,在需求响应中应充分考虑供需双方的利益平衡[9]。在文献[10]中,微电网采用了分布式日前对偶电价策略,在该策略中,运营商向用户和供应商生成电价,用户根据电价选择其最佳运营和经济利益的时间。文献[11]建立了能源拍卖市场模型,该模型不直接与电网进行交易,而是通过市场使买卖双方均可获益。文献[12-13]使用了基于价格的需求响应策略,以有效地调整可再生能源的负荷需求,同时最大限度地提高微电网的效益。文献[14]提出了电动汽车停车场微电网的两阶段经济运行框架,采用边际电价提高微电网运营商的效益,降低用户电动汽车的充电成本。文献[15]提出了一种在多个微电网之间进行能源交易的全分布式价格机制,可以最大化所有微电网参与者的收益。上述方法均采用了合理的电价机制,有效地改善了供求关系,提高了整个系统的效益。但其电价机制依赖于日前预测信息或前期优化结果,未考虑实时电价激励下微电网的需求响应问题。
本文以孤岛微电网效益最大化为目标,考虑电力用户参与电价制定的权利,基于交替方向乘子 法(alternating direction method of multipliers,ADMM)提出了一种微电网的实时经济调度分布式优化策略。该策略通过微电网内部各运营主体间的共同议价,得出微电网内部交易出清电价和交易电能量,实现各运营主体间的交易结算。与集中式方法相比,该策略中各运营主体的内部隐私和交易信息分别由各代理点负责处理,而在交易过程中各代理点间仅需交换期望的交易电价和交易电能量信息即可实现孤岛微电网效益最大化目标的分布式迭代求解。
1 基于多代理系统的微电网模型
1.1 系统结构
典型的孤岛微电网结构如图1所示。微电网通过快速开关在公共连接点(point of common connection,PCC)与电网相连进行能量交互,该开关决定了微电网是孤岛还是并网状态。PCC上有各种分支终端,由nD个分布式电源(distributed generators,DGs)、nE个储能系统(energy storage systems,ESSs)和nL个负载组成。本文假设所有的终端都位于较近的位置,从而可以忽略总线阻抗。可再生能源和储能的端子通过电力电子转换器与PCC相连,传统发电机的端子和负载分别通过电气控制柜和负载调节器与PCC相连。每个分支机构都有一个独立的本地代理点,负责分支机构的能源优化控制和外部通信。此外,代理点可以通过局域网相互交换信息。考虑到基础设施的建设成本和通信可靠性,每个代理点只与附近的代理点建立链接。
1.2 系统效益最大化模型
本文将整个系统的效益视为各代理点效益之和。因此,微电网的系统效益最大目标可以表示为
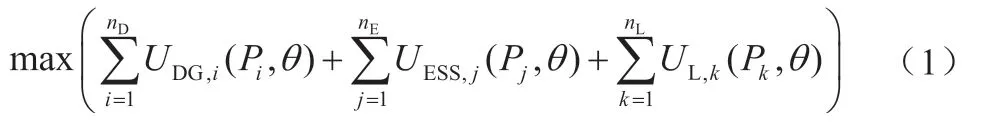
式中,UDG,i(Pi) 、UESS,j(Pj) 、UL,k(Pk) 分别为DG代理点i、ESS代理点j和负载代理点k的效益函数;Pi、Pj、Pk为i、j、k代理点中电源功率、储能功率和负载功率,Pi、Pj>0代表提供的电力,Pj、Pk<0代表消耗的电力;θ为电价,其约束为

式中,θmin为电价最小值;θmax为电价最大值。
在市场环境中,分布式电源是能源供应商,从销售能源中获益。其效益函数可以表示为
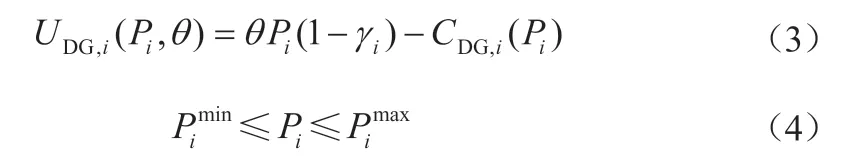
式中,γi是支路i的功率损耗百分比;CDG,i(Pi) 是DG代理点UL,k(Pk) 的成本函数;和分别是DG代理点i功率的下限和上限。
本文假设从可再生能源代理点获得的能量是免费的,即光伏和风能。由于传统发电机可以由燃料或天然气驱动,所以成本函数可建模为
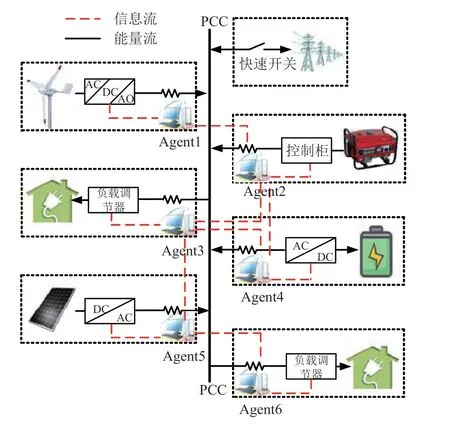
图1 MGs的典型结构Fig.1 Typical structure of MGs
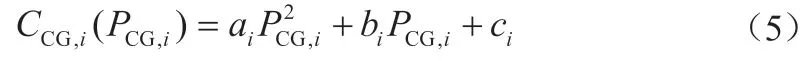
式中,ai、bi和ci为成本函数的参数。
负荷的效益函数为[16]:
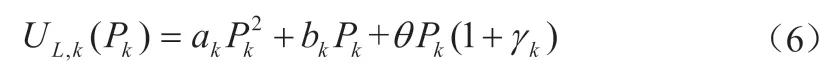
式中,ak和bk为效益函数的参数;γk为分支k的功耗百分比。此外,负荷可分为不可控负荷和可控负荷,不可控负荷对供电可靠性要求较高,不受微电网的调度。可控负荷在微电网系统优化调度中可被临时切断、调整和转移。负荷k的约束见式(7)

式中,和分别为负荷k的功率下限和上限。
储能系统获得最大效益的一般策略都是在低电价时间段充电,在高电价时段放电[17]。充电/放电动作由当前电价θ、历史电价θp k和未来电价θ fk的比较决定。历史电价是指储能系统在过去时段中购买能源的平均价格。系统服务器中存储的历史电价信息可以预测未来的价格。因此,效益函数可以建模为
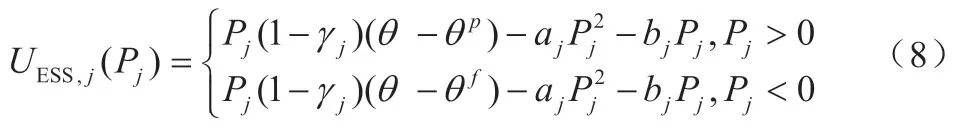
式中,γj为分支 的功耗百分比;aj、bj为效益函数的参数。充电功率的上下限约束为:

系统功率平衡约束为:

式中,∣∙∣为绝对值符号。
2 基于ADMM的功率优化方法
2.1 目标函数重构
将所有的代理点集合表示为N=nDUnEUnL。对于每个代理nϵN,将从一个代理点 到另一个代理点m的耦合功率表示为Pnm,其中mϵN、m≠n。因此,代理点n的耦合功率可以定义为

式中,dnm表示代理点n和代理点m之间的通讯状态,当dnm=1时表示存在通讯连接,否则dnm=0。若0则耦合功率为

若0则耦合功率为

此外,各代理点的理想电价定义为θn,则系统效益最大的目标函数可以重构为

式中,CONn是代理点n的一组局部约束,其包含式(2)、(4)、(7)、(9)和式(11)~(13)。
由式(14)可知,每个代理点n都有其要优化的局部变量Pnm和θn。然而,代理点n和代理点m之间成功的交易谈判需要电价θn下的耦合功率Pnm与电价θm下的耦合功率Pmn达成一致。因此,式(14)可以重新表示为:
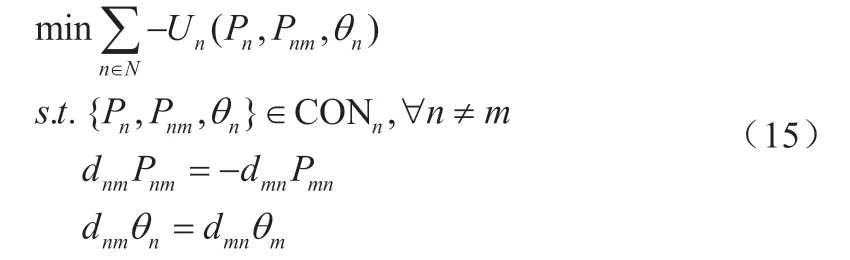
2.2 异步ADMM算法求解
针对上述具有耦合约束的分布式优化问题,ADMM是一种具有较好收敛效果的算法,考虑到实际系统中分布式同步运行难以实现,因此本文采用异步ADMM算法求解分布式优化模型。
为了简化式(15),将代理点n的耦合变量定义为一个向量xn=[Pnm,θn]T。因此,代理点n的增强拉格朗日函数可以写成:
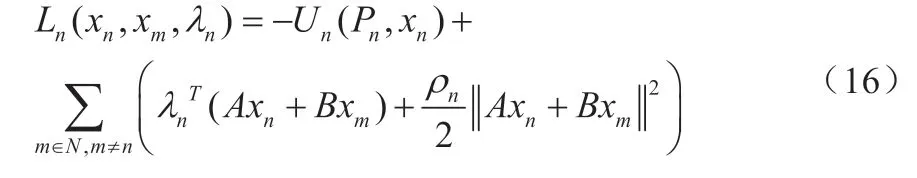
式中,λn是拉格朗日乘数A=[dnm,dmn]、B=[-dnm,dmn]的向量。ρn是惩罚参数,为了保证模型的收敛性,每个代理点的惩罚参数都要相对较大[18]。
针对增强拉格朗日函数采用异步ADMM来更新参数,可以表示为
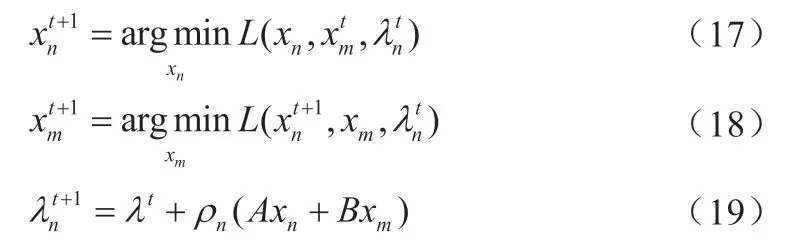
式(17)~(19)可以迭代求解,直到原始残差满足以下收敛条件:

式中,ε是一个收敛的极限值,变量Pn、xn和λn则为收敛的最优解。
表1给出了集中式优化与分布式优化下,各运营主体需要向外提供的信息对比。

表1 分布式优化与集中式优化提供信息对比Table1 Distributed optimization and centralized optimization provide information comparison
从表1可以看出,相比集中式优化,分布式优化过程中需要向外提供的信息仅为交易信息,而内部信息则不再向外提供。这种方式能起到很好的隐私保护作用。
3 算例分析
3.1 基础数据
利用Matlab2016aYalmip和CPLEX求解器进行仿真。对图1所示的孤岛微电网进行了仿真模拟,仿真包括一个PV、一个风力发电机(wind generator,WG)、一个CG、一个ESS和两个负载。表2列出了不同代理点之间的通信链路状态。
为了提高算法的收敛性和收敛速度,将惩罚参数设置为ρ=1.5,收敛阈值设置为ε=10-5。支路功率损耗系数设为γn=0.02。中国大部分地区的电价的范围为[0.3,1.3]。另外,微电网中各单位的仿真参数见表3。
3.2 仿真结果分析
在所提微电网系统中,可再生能源发电的功率被认为是不可调度的,并且总是以其最大功率运行。其他可调度单元的功率最初设置为最小功率。
微电网经济调度分布式优化中各耦合单元原始残差的收敛过程如图2所示。原始残差持续收敛,当迭代次数达到110次时,所有残差都小于10-5达到收敛。收敛过程表明,该方法能使优化变量快速收敛到目标值,适用于实际应用。

表2 通信链路状态Table2 Communication link state
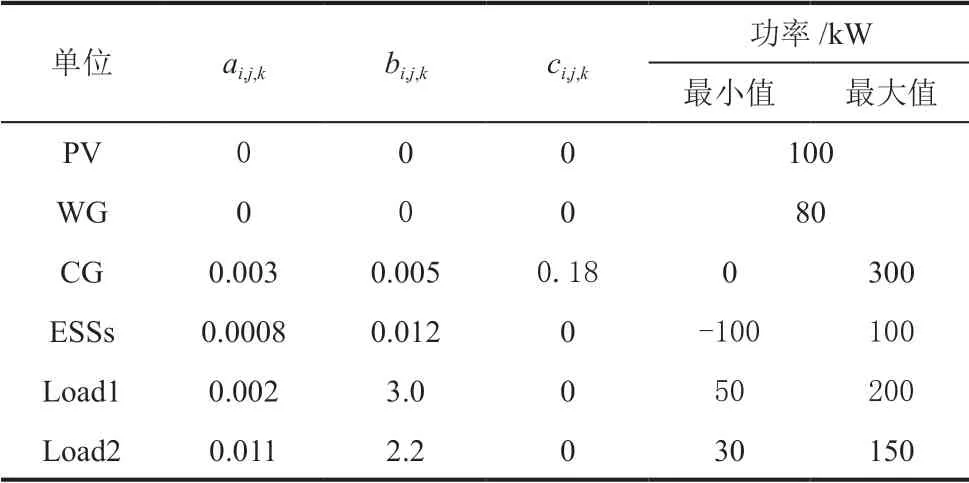
表3 仿真参数Table3 Parameters
价格和功率的收敛曲线分别如图3和图4所示。不同单元的效益函数表明,供应商总是倾向于以较高的价格出售更多的能源,而消费者总是倾向于以相对较低的电力成本消耗更多的电力,从而创造更多的效益。从图3可以看出能源供应商的价格在迭代开始时总是处于最高价格,而能源消费者的价格总是以最低价格开始。随着迭代次数的增加,供应商和消费者之间的价格逐渐接近,直到满足收敛条件为止。在迭代过程中,耦合功率和价格是相互激励的。图4中的耦合功率均以绝对值表示,可以看出,当迭代次数增加时,相邻代理点的曲线会快速地相互靠近,并在第40次迭代中相互重叠。耦合功率的重合间接地表明实现了系统功率的平衡。

图2 ADMM的原始残差曲线Fig.2 Primal residuals of ADMM
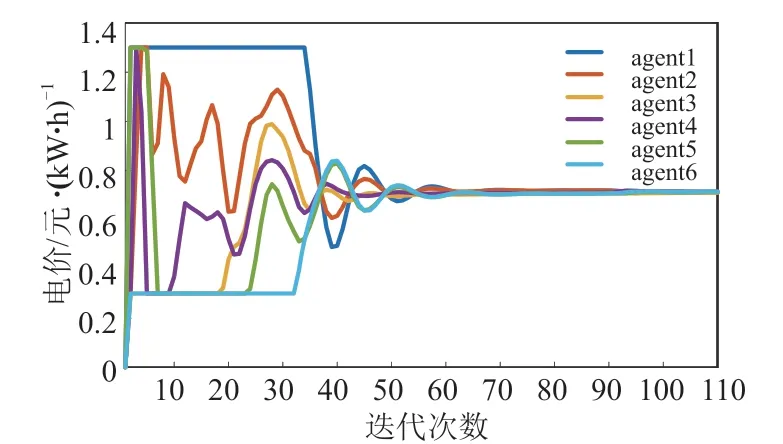
图3 各代理点电价曲线Fig.3 Prices of agents
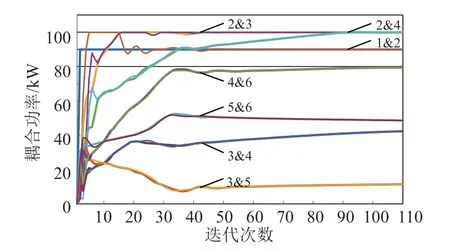
图4 相邻代理点耦合功率收敛曲线Fig.4 Coupling power of neighboring agents
为了更好地说明功率平衡的实现,分布式电源供电功率、用电单元消耗功率、支路功率损耗及它们的失配功率曲线如图5所示。功率失配曲线在第40次迭代中达到零,在第40次到第110次迭代中保持为零。虽然功率失配曲线很快达到零,但在第40次到第110次的迭代中,能量供应和消耗仍呈增加趋势,这是因为不同单元的价格还未完全收敛,一些单元的功率仍在调整,各单位功率曲线如图6所示。

图5 功率平衡实现过程Fig.5 Power balance realization process
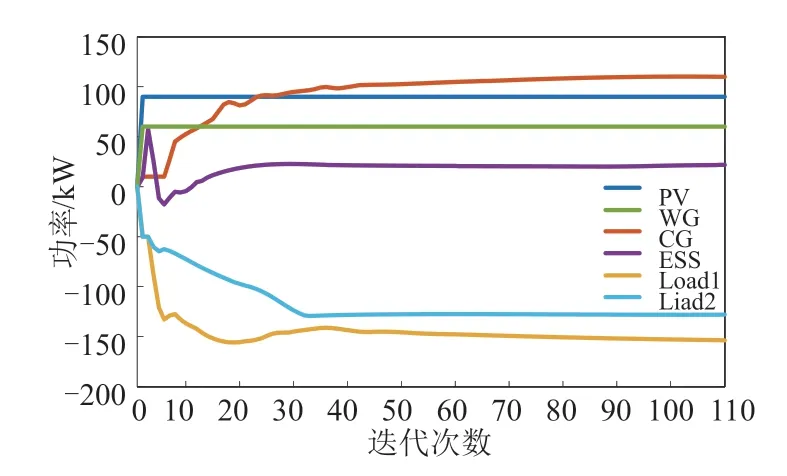
图6 各单位功率曲线Fig.6 Power of each unit
3.3 与集中式优化的比较
为了进一步证明所提出的分布式模型在系统效益最大化方面的有效性,将所提出模型与集中优化的结果行了比较,结果如表4所示。两种模型得到的系统效益差异仅为0.2%,优化电价差异为0.6%。此外,不同单元的最佳功率差异均在表4中列出,均小于1%。结果表明了所提出的分布式优化策略能获得与集中式优化方法几乎一致的优化效果。
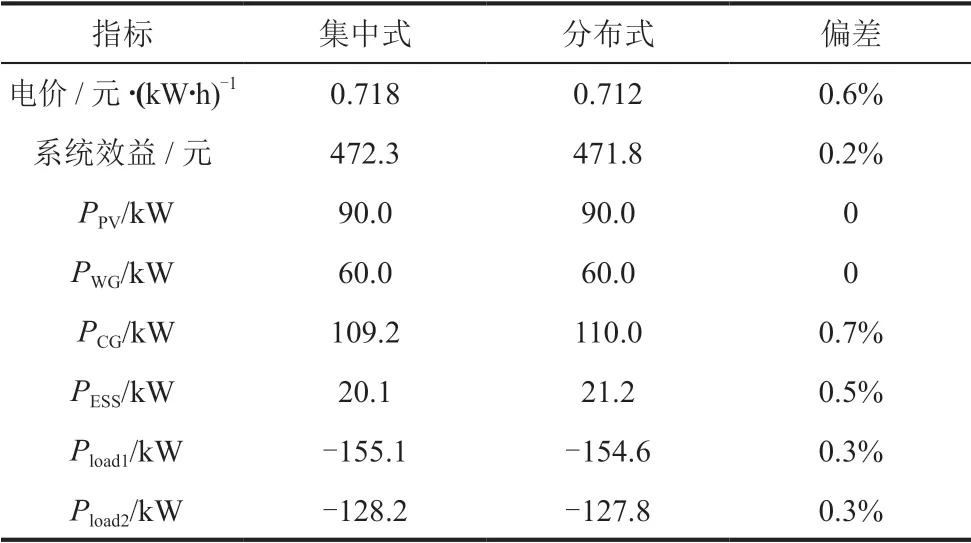
表4 效益结果对比Table4 Comparison of benefit result
这里给出了集中式方法和分布式方法的收敛时间对比结果,如表5所示。相比于集中式优化方法,分布式优化可以更快得到收敛结果,相比于集中式速度提升了29.5%。

表5 优化时间结果对比Table5 Comparison of optimization time results
4 结 论
微电网的经济优化调度是微电网的重要研究课题之一。考虑到电能交易带来的损耗,本文以孤岛微电网效益最大化为目标,提出了一种基于多代理系统的孤岛微电网实时经济调度分布式优化策略。该策略中电力用户有提交价格的权利,微电网内部各运营主体通过相互议价得出交易的出清电价和交易电能量。系统效益最大化模型采用了ADMM算法进行分布式迭代求解,在此过程中,微电网内部的交易主体仅需交换期望的电价和电能交易信息,更好地保护了交易主体内部的隐私。仿真结果表明,该策略能快速实现系统功率的平衡,减少了近30%的优化时间,并且能有效获得与集中式优化方法相同的优化效果。

