量子自旋芳草在，觅寻液态惹尘埃

刘俊明

鹧鸪天 @ 远山

年少村头望远山，灵峰直入乱云间。

日平墨影青霄卷，月吊红尘旭旦闲。

下西壑、上烟峦，方知高处复高观。

如今虹彩飘零过，不信蜃楼有绛仙。

I.引子

世间万物以对称为美、和谐为善，这是人性之愿望。不过，对“是非曲直”，人类还是更愿意赞美“是”与“直”，不喜“非”与“曲”。我们欣赏“大漠孤烟直，长河落日圆”，“直”和“圆”的景致总让人心旷神怡、赞美不已。自然科学也如此，我们喜欢对称，所以李政道、杨振宁先生提出宇称不守恒对我们的观念冲击很大。发现、揭示或证明物理上的“是”要比质疑“是”容易得多、常见得多。“是”常常皆大欢喜，“非”常常令人失望和沮丧。这可能也是一种物理观念上的不对称。我们说某件事“好”，受者高兴、施者也乐意。当我们质疑某个“好”时，往往会激起很多反驳和辩论。论证“非”很多情况下需要穷举，须穷其所能而不可挂一漏万。仔细想来，其实也没有哪一条规范、哪一部法律规定了“是”与“非”、“好”与“非好”一定要不相伯仲。其中诡异，难以述说，不知所以。

我们无妨以此为一种信念，多去审视物理学中一些质疑之声。这里展示一个我作为龙套角色亲自参与的故事，也算是对前述不对称议论的蹩脚注释。读者您会看到，在历史的长河中，常见的是润物无声，跌宕起伏自是少数。本文稍长，看君请耐心。此文在一位严谨的学者眼中可能是贻笑大方之作，无奈这是笔者的一贯风格，是为可读性而放弃严谨而已。更专业的描述也许可以参见一篇相关报道（链接：http://news.nju.edu.cn/show_article_12_48596）。

II.自旋液体

众所周知，自旋之间的相互作用及由此而生的自旋序（磁相变）似乎是凝聚态物理学的永恒主题之一。如果我们由易入难，从经典自旋系统开始，则犹太学者伊辛所完成的楞次老师布置的作业—一维自旋链是否存在相变—应是固体自旋系统“格物致知”历史之开始。我们知道，高对称点阵中，如果只考虑最近邻相互作用，则一维Ising 自旋链不存在有序态，二维点阵存在有限的相变温度并由Onsager 给出严格解、杨振宁给出相变点附近磁矩的严格解……。三维点阵中Ising 模型到目前还没有严格解，但也不妨碍近百年的数值模拟工作对三维模型的深刻物理认识。这些历史的黄金烙印奠定了经典磁学的基石。当海森堡提出自旋相互作用的量子理论后，这些烙印也可以看成是现代磁学和自旋电子学的基石，几十年来萋萋而优美、微澜而不腻。现在的理工科大学生都大致了解：只要维度超越一维，伊辛自旋系统就可能在某个特定温度处发生相变，形成长程序。

自然，有人会将伊辛模型推广到空间上自由度更多的体系，如 XY 模型、Potts 模型及至海森堡模型，后者自旋可以沿任意空间方向排列。虽然定量甚至定性上有各种风花雪月，但伊辛之名依然绰约。不过，物理学界众多好事之士茶余饭后总会提出一些新的说辞。比如说：二维、三维甚至更高维空间的自旋系统是否就一定得有序？有无极端例外，即使温度降到零度也不会长程有序？按照“引子”所述逻辑，如果能够发现“有”这个极端，那当然是皆大欢喜，比有人断言“没有”要受欢迎得多。

事实上，我们早就知道很多人在研究这个极端。例如，二维各向同性空间中海森堡自旋系统有无相变？这种问题时至今日仍然未得圆满。逻辑上，至少有两类情况可能逼近这个极端。一是空间对称性下降，一是交互作用不限于最近邻。凝聚态物理有个名词定义这种现象，叫“自旋失措（阻挫）spin frustration”。为描述简单，我们从二维伊辛模型开始。伊辛自旋只能取两重旋转对称的两个态（即只能上下取向或左右取向），一对最近邻自旋交互作用能为H =−J(Si×Sj)，其中J 为自旋交换积分（也称交换作用）、Si和Sj为近邻位置对坐标处的自旋算符，J 可以简单近似为两个位置之间距离的衰减函数。

图1 固体自旋系统中自旋失措的基本物理图像。(A) 伊辛自旋链近邻自旋相互作用类型[1]。(B) 二维三角格子的三个自旋反铁磁排列一定导致失措[2]。(C) 反铁磁三角格子单元的六种简并态[3]。(D) 如果三角格子是海森堡自旋，局域可能形成非共线有序排列[2]。

如图1(A)所示，J >0 乐于自旋平行排列，J <0喜欢自旋反平行排列，推广到长程序中即铁磁序和反铁磁序。如果J < 0 且点阵是较低对称的三角点阵时，点阵单元的三个自旋排列方式必定多于一种，点阵能量最低的基态就变得不唯一，如图 1 (B)、(C) 所示。对此三角单元本身而言，至少有图1(C)所示的六种能量相同的基态。

无需讳言，多个基态是物理学确定论大忌，会让那些“您给我一个支点，我就可以撬动地球”的物理学家心烦意乱、不知所措。如果一个无限大的三角点阵都是如此，体系的基态数目将趋于无穷，更会使物理学家芳心失常，故而将图1 (B) 所示排列取名为“自旋失措”也算形象生动。如果这个点阵中自旋按照海森堡自旋来排列，则有可能形成如图1 (D) 所示的组态；温度降到零温时，有可能形成一种非共线长程序基态。

既然如此，应该就有很多J < 0 的三角点阵伊辛自旋系统，它们即便到零温也不会有任何自旋相变出现，每个自旋仍然可以按照某种动力学模式随意转动一下（自旋所在格点位置不动）。这非常类似于我们常见的冰与水。如果水分子形成六角晶格长程排列，就是冰；但如果像水那般随机排列和“流动”，就是液态。所以，我们也许可以将一个严格正三角点阵的、J < 0为常数的系统称之为自旋液体(spin liquid,SL)。不过，毋庸长考，马上就可以断言真正的SL 态应该很难。至少有如下几个原因可以佐证这一断言：

1.对一固体系统而言，自旋交互作用能只是整个体系能量很小的一部分，原子/离子之间的结合能要大得多。从这个意义上，自旋相互作用方式从属于离子结合能。对称性破缺是固体结构的本征属性。当趋于零温基态时，晶体结构很可能出现自发对称性下降。您要找到一个几何上严格的三角点阵系统可能未必容易。如此，图1 所示之理想状况就难以浮现，一切有关SL 的物理可能就会烟消云散。

2.所谓伊辛自旋，是物理理想化的结果，是实际固体系统施加给自旋取向高度各向异性的某种近似。实际上，自旋严格满足二重旋转对称性的系统当属“此曲只应天上有”。严格的海森堡自旋体系也应是海市蜃楼，难得一见。因此，绝大多数体系的自旋对称总是介于中间某个位置，此时体系的基态简并数就会断崖式下跌。这种退简并自然就为在某个温度处出现某种自旋序提供了可能。

3.类似地，严格的最近邻相互作用系统也比熊猫数少很多。当高阶近邻半路杀出，系统也极有可能高度退简并，基态数目趋于很少，自旋序出现就不再稀奇。 至此，我们明白，对一个经典自旋体系，即便有很严重的自旋失措，如上所列三大“退简并”根源会因为某种“多以意会、难以言传”的原因压制了真正SL 态的诞生。为简单起见，我们再回到伊辛相互作用能表达式：H = −J(Si×Sj)，从能量尺度稍作讨论，请不必较真于严谨。

对经典自旋， S(i,j) = 3 ∼10 应属常见，J =−10 ∼100 meV 也很正常。注意到室温下的热涨落能量大概是10 meV。当退简并出现，一个经典自旋系统的基态与低能激发态能量差δH ∼10 meV 应属正常。此时，只要温度低于室温，不需要很低温度，体系就可能出现长程自旋有序态。此时SL 就连昙花一现的机会都没有。

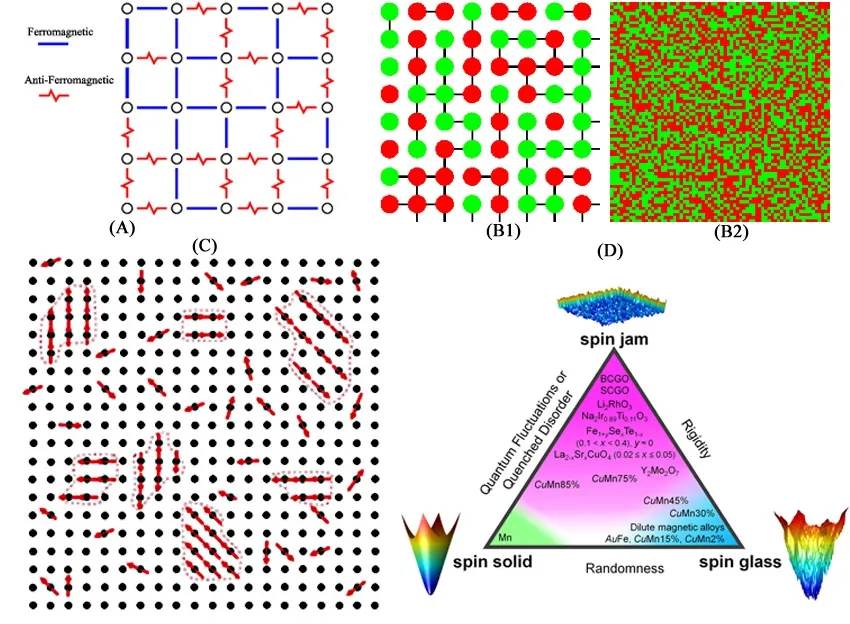
图2 经典自旋玻璃图像。(A) 示意出自旋相互作用的复杂性，每一自旋近邻对之间的J都可能不同，J > 0 和J < 0 齐飞[4]。(B1) 显示局域自旋取向，红绿表达相反的两个取向[1]；(B2) 显示大尺度自旋组态和形貌[1]。(C) 所谓的团簇自旋玻璃态，其中存在一些不同尺度的铁磁或反铁磁团簇[5]。(D) 不同自旋结构的能量大观园：长程有序态(spin solid)、自旋玻璃态SG、自旋“果冻”态(spin jam)[6]。它们构成三角，借助不同内禀或外源参量调控，可以相互转化。这里，自旋果冻态近似可以看成是我们的深闺佳人了。

诚然，实际自旋系统要复杂得多，我们已经知晓的七大姑八大姨包括：晶格对称性破缺、各向异性、最近邻、次近邻、次次近邻、次次次近邻、自旋轨道耦合、自旋晶格耦合、表面效应、杂质效应、缺陷效应、……，还可以罗列 100 个旧名词。所谓“不见新人笑、就看旧人哭”，很能描述我们此刻的心情。这些效应全部加上，系统会变得很复杂，于是物理人自作聪明创造了一个名词：无序(disordering)，来囊括这些说不清道不明的效应。这种无序有时是内禀的，无论您是否竭尽平生去提高样品质量，它就在那里。当然，这也是物理人处理复杂性的传统：我们先投机取巧一回，先将复杂物理过程用一个美的、简单的表达式表达出来，但将所有不确定和复杂性都归到表达式前面的系数中，让后人既崇拜这些优美简洁表达式的创造者、又哑巴吃黄连。

我们一切从简，假定系统真的只有一个基态。当温度下降到某个温区之内，低能激发态与这个基态之间δH 也变得很小，但自旋在基态与这些激发态之间“转一转”所需跨越的能量势垒却很高，这个温区的热涨落能量已不足以“很快”驱动这种跨越。此时，即便自旋结构处于激发态，也会在很长时间尺度内保持在那里，回不到基态。我们将这种状态称之为自旋玻璃态(spin glass,SG)。很显然，SG“不是基态胜似基态”，因为 SL 是“深闺无人晓”、SG 是“东施效颦多”，很多固体自旋系统之所以经常出现自旋玻璃态、团簇自旋玻璃态、赝超顺磁态等等局域有序或短程/中程有序态，这就是其中缘故。图2 显示出 SG 的尊容一角，详细说明可见图题，特别是图2(D)值得细细品味。

几乎所有自旋玻璃态都是亚稳定的，甚至基态也是“亚稳定”的，但保持亚稳定的特征时间可能比宇宙年龄还要长，您我有生之年难以见到，故称之为自旋冻结(spin freezing)。也如您所知，很多年来，这些自旋冻结态的学问是一部分学者在高校和研究机构赖以为生的施主，其情可鉴、其源可期。

行文到此，笔者打着自旋液体的旗号，兜售了很多自旋液体品牌下的赝品和山寨货。真正的自旋液体SL 近百年来仍然凤毛麟角，难得一窥真容。诸多尝试，皆成云烟。其实，作为一个物理学问题，自旋液体也不过是一抹阳春白雪之态，并无下里巴人之用。这许多年来，寻求SL从来就不是振臂一呼之号、也非高朋满座之所。

那么，应该怎样才能接近SL这个冷峻凤麟呢？！毫无疑问，一个系统如果 S(i,j) = 1/2，即量子自旋系统，则自旋相互作用能 H 就会变得很小。粗鲁估算一下，基态与低能激发态能量差 δH ∼0.1 meV 就不再是凤毛麟角之象了。如果基态与低能激发态之间的跃迁足够快（δt ∼ 10 −18 s 或更短，当然，对量子跃迁是不能定义绝对时间的），则量子涨落的能量δE >(h/4π)/δt ∼ 0.1 meV 并非天方夜谭。

也就是说，如果没有量子涨落，当温度降到∼1 K 左右时，一个量子自旋系统就该出现自旋有序相变了（在足够长时间尺度内）。但正因为量子涨落是天数，无处不在，相变可能就无法emerging，而被量子涨落“和谐”掉了。我们说，“柳暗花明又一村”的意境就在这里：对于一个固体量子自旋系统，可能会出现真正的SL 态，称之为量子自旋液态(quantum spin liquid,QSL)。

III.量子自旋液体

好吧，请怜悯笔者费尽口舌将QSL 可能是什么样子说了个大概。现在，物理学家终于找到一个借口，来释放自己的动力、压力和梦想，成就自己的成果、项目和荣誉。只要在量子自旋系统中细细寻觅，便可能找到一个真正的QSL 态。

问题是，与经典系统比较，量子自旋系统寻找起来更难（少！）、测量起来更贵（超低温！）、应用起来更远（人类怕冷！）。鉴于自旋玻璃和内禀无序的存在，要找到一个真实的QSL 实属不易。这也是物理人执着于求“是”的内在精髓。

如果QSL 就只是如此地阳春白雪，一定难以得到纳税人首肯。更何况如元稹所言：“曾经沧海难为水、除却巫山不是云”，那些沉迷研究SL 多年的学者们多数早就意兴阑珊、不复豪情壮志。只是，曾几何时，“英雄创造历史”的哲理再次灵验。上世纪凝聚态物理的“孤独求败”菲利普·安德森(P.W.Anderson)闭关修炼，无意间成就了一招，引得无数英雄尽折腰。

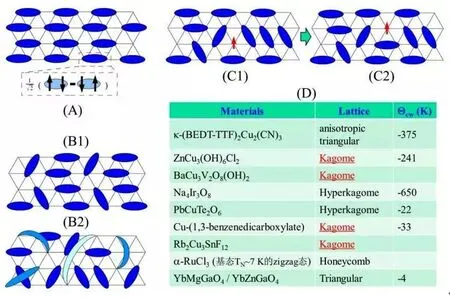
图3 量子自旋液体的基本物理图像。(A) 安德森定义的所谓共价键固体 (VBS)，其中一对最近邻自旋反平行排列成键，形成spin-0 singlet。这些单态有序排列，形成VBS。此时，有序单态排列导致点阵对称性破缺，因此不是 QSL 基态。(B1) 共振共价键态时短程相互作用形成的自旋对组态。(B2)考虑了长程相互作用时自旋对的组态，即真实的共振共价键态 RVB。(C) 所谓的自旋子激发态的图像。RVB 态因为长程关联而可能出现共价键的瞬间“断裂”与“复原”，产生一个不带电荷、只有1/2 自旋到处游弋的状态，即自旋子激发态。从(C1) 到(C2) 图示了自旋子激发态游弋一步的想象过程。(D) 部分声称可能实现QSL的体系列表，每一种到底是不是QSL 其实存在不少争议。[7]

QSL 态作为固体自旋系统的基态由安德森在1973年提出，对象是最近邻反铁磁三角点阵。首先，既然是反铁磁基态，体系零温下不能有剩余磁矩，因此安德森使用了共价键态(valence bond state) 的概念，即点阵中两个电子自旋总是两两成键，构成一个自旋为零的单态(spin-0 singlet)，整个点阵即为非磁，如图3 (A)所示，称为共价键固体(valence bond solid,VBS)。其次，VBS 本身并非 QSL，因为所有 spin-0 singlets 有序排列，点阵对称性必然破缺，与QSL 的图像矛盾。再次，在基态下，这一共价键固体的自旋缺乏长程关联或纠缠，而安德森眼光很高，觉得这一基态物理意义不大。由此，他放松管制，引入共价键的量子涨落，从而将实空间的共价键点阵与动量空间的纠缠关联相联系，真是天才的想法！此时，每一个共价键就不再只是最近邻两个自旋的反铁磁耦合，还要接受整个点阵中所有自旋组态配分的恩赐。

安德森进一步假定，所有自旋组态配分的效果都一样，即量子涨落幅度一样，那么任何共价键就不再只具有局域空间的特征，而是反映整个空间的叠加效果。这一假定对熟悉量子力学的人而言非常自然，就像潘建伟1200 公里量子态叠加纠缠。此乃安德森喜欢的基态，即共振共价键(resonating valence bond,RVB)态，如图 3 (B1) 和 (B2) 所示。安德森敲定，这就是他要的量子反铁磁三角点阵的基态。

熟悉超导BCS 理论的读者一定已经明白：超导体中电子通过动量空间的声子关联，形成库珀对（自旋相反的一对电子在动量空间成对），这个库珀对也是spin-0 singlet。这一图像与这里的基态如出一辙。考虑到高温超导铜氧化物具有量子磁性，考虑到超导态必须抗磁或者至少无磁性，安德森大胆预言：QSL 这一基态就是高温超导母体的基态，只要加入可动载流子，就可以“超导”了！用南京大学王强华的话说：高温超导就是QSL。

好了吧，全世界那些武装到牙齿的高温超导团队听说安德森写了这么一部“葵花宝典”，会善罢甘休？！他们如狼似虎一般，使出浑身解数，再难再苦，掘地三尺，也要找到 QSL。如此这般，QSL 不火都不行吧？！除此之外，安德森描述的长程量子关联图像也很对那些借助量子纠缠来实现量子计算的梦想家之胃口。QSL 中存在一种任意子激发（自旋子spinon 激发，可见下文），操作任意子以实现量子计算是大家正在设想的方案。如果能够找到一些在相对高的温度下依然稳定的QSL，利用其中的任意子激发和量子纠缠实现高效量子计算，也是功德无量的善事。因此，量子计算也是驱使物理人对QSL 趋之若鹜的推手，虽然笔者不懂这一梦想是白天做还是晚上做比较靠谱，所以决不能说这是白日做梦！

无论如何，我们可以相信，高温超导和量子计算如倚天、屠龙，双剑一出，纳税人就会乐意支持。这就给了QSL 在过去十年“金沙水拍云崖暖、大渡桥横铁索寒”的风光。

IV.判定量子自旋液体态

我们反复强调了寻找 QSL 很难，因为您不可能真的去零温下探测QSL 基态。退而求其次的方法是，在很接近QSL时通过测量一些低能激发态下的物理量，由此外推到零温，来判定我们是不是找到了一个真的QSL。 一方面，这是物理学研究的逻辑，甚至从牛顿使用微积分时就是如此逻辑，屡试不爽。另一方面，这样一个物理量必须有独特的特征，是其它自旋态如自旋玻璃等不会有的特征量。我们来看看，QSL 的低能激发态是不是有这样一些特征量if any，虽然很难。

经过多年理论摸索，QSL 一个非常重要的特征是具有分数化的激发。一种典型的分数化激发是自旋为1/2 (spin-1/2) 的自旋子 (spinon)，对应于 RVB 模型中的spinon 激发。自旋子不带表观电荷，但携带1/2自旋，图像如图3 (C) 所示。由于QSL 是长程自旋关联的叠加共价键态，这些共价键态在低能激发下很容易瞬间“断裂”与“复原”，表现为一个孤单的“1/2自旋”游弋于点阵格点中。注意，电子是局域不动的，这里不是电子游弋，是表观上有一个“1/2 自旋”在点阵中游荡。这种状态就是所谓的自旋子激发态。

基于前面不厌其烦的讨论，我们可以罗列几个特征量来测量了。遗憾的是，到目前为止，任何一个单一量的测量都不足以判定 QSL，必须像治疗“艾滋病”那样，用鸡尾酒疗法，通过很多特征量，综合诊断才可能不出差错。这其实是物理人的某种“悲哀”，违反了我们追求优美和简洁的哲学。这些可测量量表述为：

1.强烈的自旋失措特征：失措参数 f = |θcw|/Tc>100，这里 |θcw| 是外推的居里–外斯温度， Tc是测量的磁有序温度。

2.极低温核磁共振 NMR 或者谬子自旋共振 µSR测量：只要系统出现磁有序，就会有内禀等效磁场，NMR 或 µSR 就可以测量到。

3.极低温比热测量：与理论模型比对，判定磁涨落的贡献。

4.极低温热导测量：判定低能激发是局域的还是巡游的，这在热导率上有灵敏表现。

5.中子散射测量：QSL 的自旋子激发类似于巡游电子，具有自己的色散。两个自旋子的束缚态对应于自旋为1 的磁振子激发。中子散射对这些激发都很敏感，特别是非弹性中子散射连续谱被认为是迄今为止最为可信的量子自旋液体判据。

6.光电导反射谱测量：这是判定自旋子是否存在的技术。如果存在，光电导应该满足幂指数律。

我们看到，上面所列每一项都是可能“令人失措”的测量，所以f > 100 合情合理、理所应当，也印证了为什么探测QSL 是如此艰难。

啰嗦到此，我们该回归主题、讲述我们的故事了。阿门！

V.质疑之路

2003 年报道了第一个可能的QSL 体系，即有机体κ-(BEDT-TTF)2Cu2(CN)3。至今声称可能是 QSL 的材料数目也不过个位数，可见夺取“葵花宝典”之难。

最近两年，有几个很深入的工作报道三角格子系统YbMgGaO4(YMGO) 可能是一个理想QSL，获得了很高关注度。这些工作基本覆盖上述六项测量数据，结果看起来毋庸置疑，也触发了后来者效仿YMGO 去探索类似体系是不是QSL。

不过，如果仔细斟酌这一体系，您会觉察到稍有不妙，存在一些疑点：

1.YMGO 的 J ∼ 1.5 K ∼ 0.15 meV，实在是太小了，可靠灵敏的测量变得很关键。

2.Mg2+与Ga3+占位完全无序，这一体系存在内禀无序无疑。这一因素很容易引起熟悉材料结构的学者警觉。尽管Mg2+/Ga3+位于非磁层， J很小时无序的能量尺度不再可以忽略。

3.热导测量 [Phys.Rev.Lett.,2017,117:267202]没有看到来自磁激发的贡献，而其磁激发应该是gapless 的。这一结果对无能隙QSL 态提出很大质疑。

南京大学温锦生教授及合作者正是质疑者之一支。他们希望理解YMGO 到底是不是QSL 基态；如果不是，基态是什么？他们生长了高质量YMGO 单晶。为了慎重起见，他们又生长了一种与YMGO 非常类似的新三角晶格单晶YbZnGaO4(YZGO)，以资比对和交叉检验。随后，整个团队开始了“漫长而艰辛”之测试分析历程，包括直流磁化率、极低温磁比热、磁弹性和非弹性中子散射、极低温热导、极低温交流磁化率测量，也包括详细的理论分析与模拟比对。这里，笔者不论测量结果和数据分析细节，只是将有关YZGO 的结论提取出来。对YMGO，结果完全是类似的。看君有意，当可审阅作者见刊不久的论文[Phys.Rev.Lett.,2018,120:087201]。

1.在50 mK 以上温区，未见磁有序和磁相变特征，磁相互作用J ∼1.73 K。

2.弹性中子散射揭示无长程自旋序；非弹性中子散射揭示沿布里渊区边界有很宽的连续激发谱，一直延续到带顶1.4 meV，看起来似乎很QSL。

3.理论上，基于已有模型添加无序效应，不难获得中子散射看到的连续谱，与实验结果定量一致。

4.热导结果没有任何巡游准粒子迹象，不支持无能隙QSL 模型，却符合无序导致自旋玻璃态的图像。

5.极低温、高质量的交流磁化率数据揭示出，存在100 mK 以下且高度频率依赖的宽峰，这是自旋玻璃的典型特征。

6.以上所有数据看起来都可以用自旋玻璃基态来完美诠释。

上述质疑的一个重要结论是：在阻挫与无序存在时，YZGO 的基态就是自旋玻璃态。特别是，确定QSL 的最有力证据――中子散射连续谱――可以由自旋玻璃态产生。事实上，这一结论同样适用于YMGO。

图4 温锦生等质疑之声落脚PRL。

这是一项很有价值的、质疑“是”的范例，而温锦生及合作者团队为此付出了巨大努力和代价。他们反复往来的重复性、极低温测量，耗费资源，积累的数据巨大，令人印象深刻。不过，与这些测量付出的心血精力比较，温锦生他们发表这一质疑结果之路显得漫长而无望。在这一进程中，他们既遭遇尖锐的批评，也得到很多未置可否似是而非的意见，虽然最后还是落脚于 PRL 上，如图4。

这些批评和遭遇其实可以理解，因为您声称“是”，可能一个证据就够了，虽然严谨性可靠性值得商榷。但如果您质疑“是”，您就得穷举当前之所能及。有意思的是，这一现状与数学之路似乎不同，与逻辑推论也有所相悖。数学和逻辑告诉我们：推翻一个结论，一个例外就够了；而证实一个结论，可能需要穷举。

随着时光推移，陆续有不少知名团队也加入质疑之声，包括国外知名理论研究组最近的工作 [Phys.Rev.Lett.,2017,119:157201 arXiv:1801.06941]。这些工作的结论实际上更为大胆，不但直言基态就是自旋玻璃，还煞有介事地讨论追求 QSL 的意义。所以，笔者将本文标题取为“量子自旋芳草在，觅寻液态惹尘埃”。看起来，QSL 目前还在“海角天涯无觅处”，需要耐心和机遇。

行文到此，故事之外应该收获一些感想与启示。笔者不才，无法罗列一二，权且滥竽充数，以慰丹心。首先，寻找固体中QSL 之路还很漫长。在这一进程中，我们明白，一种重要的物理性能，它的时间平移对称性是重要的，意味着稳定性。我们也明白，一种重要的物理功能，它的能量空间局域性也是很重要的，也意味着稳定性。图2(D)中，我们看到spin glass 和QSL(spin jam) 之间并无高山，两者联通起来不难，值得斟酌。其次，技术上实现的价值也需要推敲。稍微复杂一点的自旋失措体系，内禀无序总是存在的、且与量子涨落可比拟。这对QSL 的技术实现价值提出了很大的疑问。

作为结语和题外话，我们说凝聚态物理研究之路正在走向深入和极端，给揭示“是”与论证“非”带来了不同的时空坐标。这一状况之多面风景，看起来并不是那么顺风顺水，需要行者更加投入与付出。基础研究如此，社会生活可能将更是如此。后记：感谢几位同行同事审阅本文的学术内容，但文责错误由笔者负责。