非周期量化间歇控制的复杂动态网络同步分析

吴冬梅，丰建文，王劲毅，赵 毅

深圳大学数学与统计学院，广东深圳518060

复杂动态网络是由数量巨大的节点和节点间连边所构成，其结构、动力学演化及网络结构特征与节点动力学间关系等的复杂性，使其成为非线性科学的研究热点之一，特别是网络同步现象受到多个学科的广泛关注[1-3]，这主要是由于它不仅在神经网络系统[4]、生物学反应系统[5]、安全通信[6]、图像处理[7]及自动控制[8]等许多现实人造系统领域具有广泛应用，而且在理论上具有极强的挑战性. 迄今为止，网络同步的研究已提出多种同步模式，如指数同步[9]、完全同步[10]、簇同步[11]、相位同步[12]、拟同步[13]、广义同步[14]及有限时间同步[15]等，并涌现大量优秀研究成果.

随着对复杂动态网络同步问题的深入研究，网络数学模型也在不断改进，日趋符合现实网络，在网络同步的相关研究中，人们不仅考虑网络结构变化，且越来越关注网络运行因素的影响. CHEN等[16]研究带有多时滞的反应耗散神经网络；ZHOU等[17]讨论带有输入和输出时滞的线性系统；LI等[15]研究带有时变时滞非线性系统的有限时间同步，但忽略了网络节点间时滞的影响，这主要是由于网络运行中信道不畅导致节点间传递信息产生的滞后，并与时间密切相关. 本研究的网络模型同时考虑网络节点间信息传递无时滞和有时滞的情形，所考虑的时滞是时变的.

网络同步一般通过对其实施外部控制实现，各种控制策略，如状态反馈控制[17]、自适应控制[18]、脉冲控制[19]及间歇控制[20]等已成功用于网络同步中．间歇控制由于其控制成本低，容易实施且具有较强的鲁棒性，而颇受青睐. LIU等[21]基于周期间歇牵制控制策略研究有向网络的簇步．但周期间歇在现实中的应用是不合理或不必要的，非周期间歇更符合实际系统，如风能发电或太阳能发电系统是经典的非周期间歇控制系统．因此，将非周期间歇策略应用于网络同步研究，具有更强的现实意义．2015年，LIU等[22]成功将非周期间歇控制用于一类带有时滞非线性复杂网络的同步问题. LIU等[23]利用非周期间歇牵制控制，研究混合耦合动态网络的同步. 为进一步节省通信通道和带宽，提出对数量化控制器用来研究各种不同类型耦合系统的稳定和同步问题. 对数量化控制器是一类比较特殊的非线性量化器，由于其具有密度小等优点，近年受到学界关注. XIAO等[24]基于量化数据采样控制研究混沌Lur’s系统的稳定性问题；SONG等[25]通过量化输出反馈控制考虑非线性系统的稳定性；XU等[26]基于量化间歇牵制控制考虑网络的有限时间同步.充分考虑到非周期间歇和量化控制的优势，将它们有机结合来研究网络同步可以有效减少系统的量化误差、降低消耗、减少成本和提高效率等，具有重要理论意义和应用价值.

受到上述分析及相关研究的启发，本研究利用非周期量化间歇控制，讨论一类节点间同时具有无时滞和时变时滞耦合网络的同步问题，该网络的节点动力学也具有时变时滞．通过构造适当的时间依赖Lyapunov函数，经过严格理论分析，得到实现该类网络同步的若干充分条件．通过数值模拟验证结果有效．

1 模型描述

考虑含N个节点且带有线性耦合耗散的时变时滞动态网络，

(1)

(2)

系统(1)满足初值：xi(s)=φi(s),s∈[-τ,0]. 为实现网络同步，记ei(t)=xi(t)-π(t)为网络同步误差，设计非周期间歇量化控制器，

(3)

其中，ki为状态反馈控制增益；S={±ϖi:ϖi=ρiϖ0,i=0,±1,±2,…}∪{0},ϖ0>0为量化水平集；q(·):R→S为量化器，q(ei(t))=(q(ei1(t)),q(ei2(t)),…,q(ein(t)))T是随机且时变的，满足q(-v)=-q(v).

对于任意的v∈R相应的量化器设计如下，

记δ=(1-ρ)/(1+ρ)

(4)

其中， 0<ρ<1. 根据文献[27]可知系统存在菲利泊夫解，即存在Δ∈[-δ,δ]满足q(v)=(1+Δ)v.

注1控制器(3)通常被称为量化控制器，与连续的间歇控制器相比更符合实际. 现有工作中的控制器大多为线性连续的，这将导致所得结果比较保守. 如文献[11]采用一般的比较传统的控制策略，即

(5)

由于实际的控制系统和信息交流通道有限，使得信号量化在实际使用中非常必要.为叙述方便，记

τ1(t)))-f(t,π(t),π(t-τ1(t))).

由系统(1)和式(2)可得误差系统为

(6)

式(6)又可改写为Kronecker积的整体形式，

(7)

其中，W(t)=κ1T-K(I+Λ(t))；Λ(t)=diag(Λ1(t),Λ2(t),…,ΛN(t))；Λi(t)=diag(Δi1(t),Δi2(t),…,Δin(t))，Δij(t)是菲利泊夫解满足Δij(t)∈[-δ,δ].

令F(t)=Λ(t)δ-1， 则有F(t)FT(t)≤I.

与本研究相关的假设、定义及引理如下．

假设1对于向量值函数f(t,x(t),x(t-τ(t)))，存在正常数ε1和ε2和正定矩阵P， 使得对于任意的x(t),π(t)∈Rn， 有(x(t)-π(t))TP[f(t,x(t),x(t-τ(t))-f(t,π(t),π(t-τ(t)))]≤ε1(x(t)-π(t))TP(x(t)-π(t))+ε2(x(t-τ(t))-π(t-τ(t)))TP(x(t-τ(t))-π(t-τ(t))).

假设2[22]存在2个正数θ及ω， 满足0<θ<ω， 则对于l=0,1,2,3…， 有

注2假设2表明每个控制区间的时间长度不会小于θ， 而休息区间的长度不会大于ω-θ．

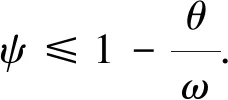
引理1[28]若给定合适维度的对称矩阵E和G， 矩阵F满足FTF≤I， 且存在标量ε>0， 则有GFE+ETFTGT<εGGT+ε-1ETE.

引理2[24]若对于给定具有合适维度的矩阵ψ、F、E及G满足FTF≤I, 且存在标量ε>0， 若Ψ+εGGT+ε-1ETE<0， 则Ψ+GFE+ETFTGT<0.

引理3[23]若函数y(t)连续且非负，t∈[-τ,+∞)， 满足

其中，a1,a3,b及c为正常数.对于非周期间歇控制，存在常数0≤ψ<1， 若满足ρ=a1+a3>0，a1>b*=max{b,c}>0，ϖ=λ-ρψ>0，则

其中，λ>0是方程λ-a1+b*eλτ=0的唯一正解.

2 非周期间歇量化控制的复杂网络同步分析

利用非周期量化间歇控制实现所讨论的网络同步问题. 为便于表述和计算，记*表示对称矩阵中的对称部分. 采用适当的时间依赖李雅普洛夫函数，首先，定义分段线性函数

定理1若假设1和假设2成立，并且存在正常数a1、a3、b1、b2、c1、c2、η， 及给定的正定矩阵P1和P2满足

(8)

(9)

(10)

(11)

a1>b*,ρ=a1+a3,ϖ=λ-ρψ>0

(12)

Φ11=2ε2P1-b1λI；Φ12=2ε2P2-b1λI；

Φ21=2ε2P1-c1λI；Φ22=2ε2P2-c1λI；

λ=min{λmin(P1),λmin(P2)}.

【证】定义时间依赖的Lyapunov函数

V(t)=eT(t)P(t)e(t)

V(t)沿着误差系统(7)求导，当t∈(tl,sl)时，

κ2He(t-τ2(t))]

(13)

根据假设1，可得

ε1eT(t)P(t)e(t)+

ε2eT(t-τ1(t))P(t)e(t-τ1(t))

则式(13)可写为

2ε1eT(t)P(t)e(t)+

2ε2eT(t-τ1(t))P(t)e(t-τ1(t))+

2κ2eT(t)P(t)He(t-τ2(t))=

a1P(t)]e(t)+eT(t-τ1(t))[2ε2P(t)-

b1P(t-τ1(t))]×e(t-τ1(t))-b2eT(t-

τ2(t))P(t-τ2(t))e(t-τ2(t))+

2κ2eT(t)P(t)He(t-τ2(t))-

a1eT(t)P(t)e(t)+b1eT(t-τ1(t))P(t-

τ1(t))e(t-τ1(t))+b2eT(t-τ2(t))P(t-

τ2(t))e(t-τ2(t))≤

eT(t)Ξ1(t)e(t)+eT(t-

τ1(t))Φ1(t)e(t-τ1(t))-b2λeT(t-

τ2(t))e(t-τ2(t))+2κ2eT(t)P(t)He(t-

τ2(t))-a1V(t)+b1V(t-τ1(t))+

b2V(t-τ2(t))

(14)

进一步将式(14)改写为

b1V(t-τ1(t))+b2V(t-τ2(t))≤

ξT(t)Ξ(t)ξ(t)-a1V(t)+

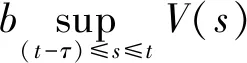
(15)

根据引理1，有

εM(t)MT(t)+ε-1EET

(16)

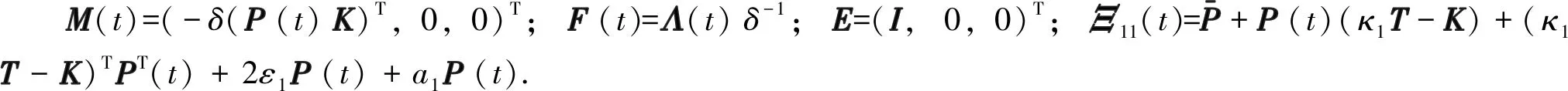
记

α1(t)ΞP1+(1-α1(t))ΞP2

(17)

结合Schur补引理和定理中条件(8)和(9)有

εM(t)MT(t)+ε-1EET<0.

于是，根据引理2可得Ξ(t)<0. 因此，式(15)变为

(18)

同理，当t∈[sl,tl+1)时，

2ε1P(t)-a3P(t)]e(t)+

eT(t-τ1(t))[2ε2P(t)-c1P(t-τ1(t))]

e(t-τ1(t))-c2eT(t-τ2(t))P(t-τ2(t))

e(t-τ2(t))+2κ2eT(t)P(t)He(t-τ2(t))+

a3eT(t)P(t)e(t)+c1eT(t-τ1(t))P(t-

τ1(t))e(t-τ1(t))+c2eT(t-τ2(t))P(t-

τ2(t))e(t-τ2(t))≤

eT(t)Ξ2(t)e(t)+eT(t-τ1(t))Φ2(t)e(t-

τ1(t))-c2λeT(t-τ2(t))e(t-τ2(t))+

2κ2eT(t)P(t)He(t-τ2(t))+a3V(t)+

c1V(t-τ1(t))+c2V(t-τ2(t))≤

ξT(t)Ξ*2(t)ξ(t)+a3V(t)+

c1V(t-τ1(t))+c2V(t-τ2(t))≤

ξT(t)Ξ*2(t)ξ(t)+a3V(t)+

(19)

其中，

(20)

注意到由式(10)和式(11)可得

(21)

最后，根据引理3，以及条件(12)、(18)和(21)，当t>0,ω=λ-ρψ>0时，有

由定义可知，系统(1)达到同步. 证毕.

当系统不含耦合时滞时，即τ2(t)=0， 系统(1)变为

(22)

则得到以下推论.

3 数值模拟

考虑由10个节点构成的带有时变时滞的复杂动态网络，且每个节点的维数为2，系统模型为

i=1,2,…, 10

(23)

其中，xi(t)=[xi1(t),xi2(t)]T,i=1,2,…,10； 耗散耦合矩阵T和H分别为

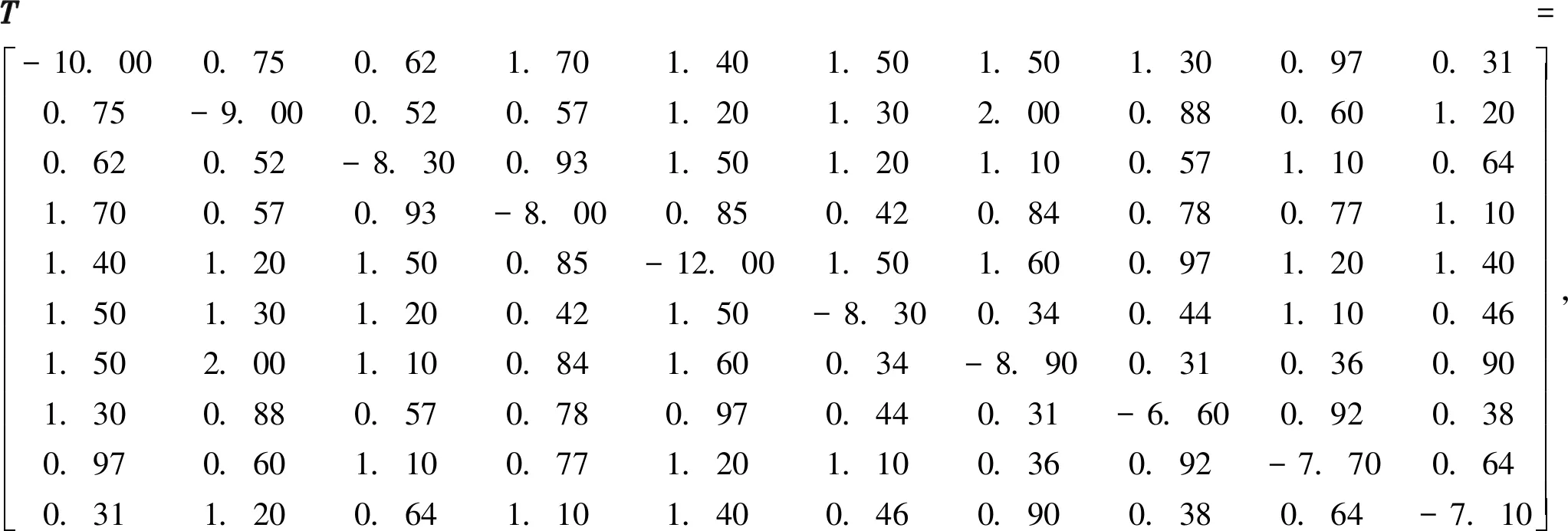
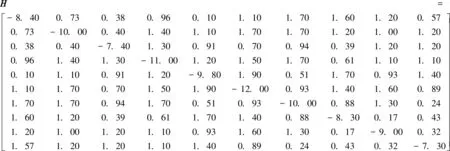
系统初值条件是随机的，内部耦合矩阵Γ=diag{1,1}， 耦合时滞分别为

k=diag{18,13,15,9,24,21,47,32,16,8}为量化控制增益矩阵.考虑非周期间歇控制，这里θ=2，ω=2.7，ψ=0.08， 为满足定理中的条件，通过Matlab计算，得到a1=0.3、a3=20、b1=12、b2=3、c1=37、c2=30、κ1=0.01、κ2=0.03及ε1=ε2=1, 由λ-a1+b*eλτ=0, 可得λ=1.98>0. 根据计算可知满足同步条件a1>b*=15>0.ρ=a1+a3=20.3>0,ϖ=λ-ρψ=0.356>0. 给定正定矩阵P1和P2为

P1=diag(3.04,3.00,4.70,2.00,6.50,4.30,1.00,9.00,5.09,10.00,1.20,3.60)

P1=diag(4.00,0.20,9.70,3.00,0.65,3.00,1.80,9.40,0.09,1.00,2.00,5.60)

由计算可得λ=3.07. 图1(a)和(b)分别为节点误差量化控制器q(ei1(t))和q(ei2(t))随时间的演变图，且最终趋于同步. 图2为系统最终同步误差e(t)随时间演变轨迹图. 可见，系统误差e(t)最后趋于同步. 所以，复杂动态网络系统(23)在非周期量化间歇控制器下最终达到同步.

图1 量化控制器q(ei(t))随时间的演变Fig.1 (Color online) Evolution of quantization controller q(ei(t)) over time

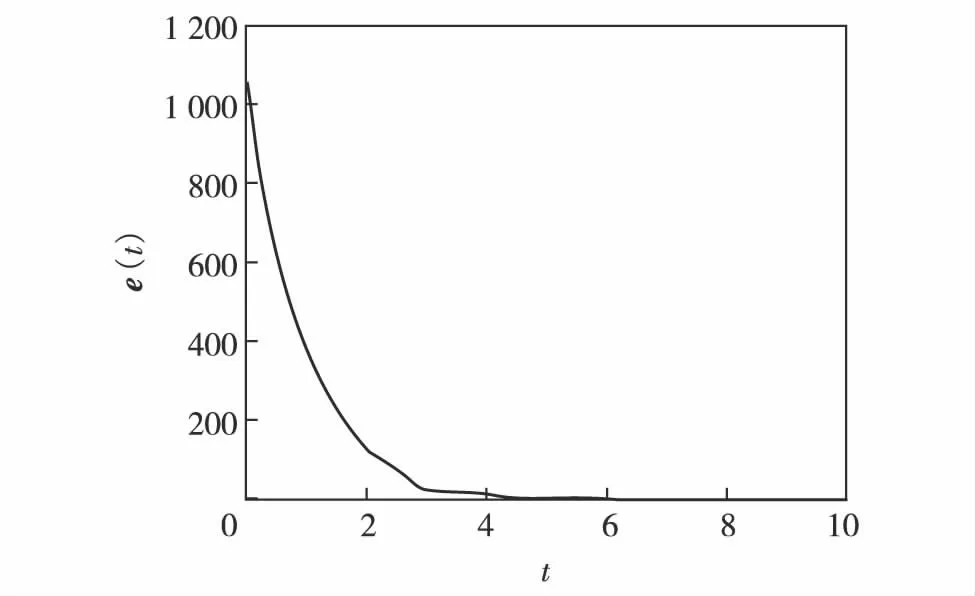
图2 同步误差e(t)随时间的演变Fig.2 Evolution of synchronization error e(t) with time

结 语

本研究考虑一类带有多重时变时滞的非线性耦合复杂动态网络的指数同步．将非周期间歇控制和量化控制相结合，采用非周期量化间歇控制策略，结合Lyapunov稳定性理论、矩阵理论等知识，设计与时间依赖的Lyapunov函数，通过严格的理论分析和证明，实现网络的指数同步．最后，通过Matlab数值模拟，验证所得结果的有效性.