基于Ansoft Maxwell的电磁阀驱动优化

杨琪 杨凯 王刚 曾云 刘洪材 刘诗凡 吴春林

摘要：电磁阀是决定柴油机电控燃油喷射系统性能的关键部件，其快速响应特性是燃油喷射系统供油稳定性的重要保证，其中驱动电压的大小是电磁阀响应时间长短的主要影响因素。通过 Ansoft Maxwell 进行磁场的仿真可以计算得出线圈匝数、驱动电压、驱动电流与电磁力、响应时间的关系，从而优化选出线圈匝数与驱动电流和驱动电压的最佳组合。

关键词：电磁阀;电控燃油喷射系统;线圈匝数;驱动;响应时间

中图分类号：TK422 文献标志码：A

文章编号：2095-5383（2019）02-0034-04

Abstract：The electromagnetic valve is a key component that determines the performance of diesel electronic control fuel injection system. The fast response characteristic of the electromagnetic valve is an important guarantee for the fuel supply stability of the fuel injection system. The magnitude of the driving voltage is the main influence factor of the response time of the electromagnetic valve. The simulation of the magnetic field through Ansoft Maxwell can calculate the relationship between the number of coil turns， the drive voltage， the drive current and the electromagnetic force， and the response time， so that the optimum combination of the number of coil turns， the drive current and the drive voltage can be obtained.

Keywords：

electromagnetic valve; electronic control fuel injection system; coil turns; drive; response time

隨着车辆行业的迅速发展，对柴油机性能的要求越来越高。电控燃油喷射系统成为柴油机排放的必然趋势[1-3]。其中，电磁阀是电控燃油系统的核心部件，其响应特性是整个燃油喷射系统工作稳定性的保证。目前，燃油喷射系统在低转速小脉宽情况下出现供油不稳定，为了减小这种不稳定情况，本文在线圈匝数、驱动电流和驱动电压上进行计算分析，选出合适的匝数、电流和电压值，提高电磁阀的响应特性，得到稳定的喷油量。

在提高电磁阀响应特性上，Cheng等人[4]研究了4种电压驱动波形情况下喷油器电磁阀的损耗情况，最后优选出了损耗最小的电压波形，并将计算值与实验值进行了对比，验证了计算值的可靠性。Tsai等人[5]设计了一种新的驱动电路，以满足汽油直喷中更快速更精确控制，结果表明驱动策略对稳定和精确注射量具有非常重要的意义。Watanbe等人[6]对电路模型进行了优化，通过电磁场的瞬态仿真，开发了一种新的喷油器，其响应时间得到了明显提高。袁海军等人[7-10]采用Maxwell软件计算了不同工作气隙、不同驱动电压等条件下电磁阀静态和动态特性。夏胜枝[11-12]及李春青等人[13]研究了电控单体泵电磁阀的动态响应特性，研究发现影响电磁阀关闭速度的主要因素是驱动电压的大小，影响电磁阀开启速度的主要因素是回位弹簧的预紧力。

通过以往的研究发现，驱动电压是影响电磁阀响应的主要因素，因此本文从线圈匝数出发，研究驱动电压和驱动电流对电磁阀响应的影响。

2 理论依据

2.1 电磁阀工作原理

电控单体泵电磁阀结构如图1所示。

电磁阀工作原理：接通电源后，电流通过电磁铁线圈，产生电磁力，吸引衔铁，同时带动运动件（衔铁、衔铁螺钉、弹簧、弹簧座、阀杆）运动，当电磁力克服弹簧力时，阀杆开始动作至阀关闭;当断开电源，阀杆在弹簧力的作用下返回，使阀开启。

2.2 电磁阀运动特性方程

电磁阀通电，阀杆关闭过程：

电磁阀断电，阀杆开启过程：

其中：m为运动件质量;a为运动质量加速度;Fmag为电磁力;Fs为弹簧力;Ff为液体阻力;

2.3 电磁阀电磁特性方程

设衔铁运动过程中磁通不变，衔铁所需的机械功完全由磁能转化而来。忽略漏磁通，认为全部磁通都通过气隙δ，当衔铁在恒定磁场中位移dδ，吸力Fmag所做的功由气隙体积内存储的磁能转化而来，即[14]：

截面积S的气隙中磁场能量：

其中：B为磁感应强度，T;S为电磁作用面积，m2;μ0为空气磁导率，H/m;δ为气隙，m;Φ为磁通量，Wb;i为线圈电流，A;N为线圈匝数;Ud为外加驱动电压;L为线圈电感;R为电阻值。

电流变化主要由外加驱动电压和线圈电感决定。提高驱动电压，减小线圈电感可以提高线圈电流变化率，缩短关闭时间[11]。线圈电感与线圈匝数相关，匝数越少，电感越小，但是匝数减小，电磁力会相应减小，关闭时间增加，这样就会出现矛盾。因此，为提高电磁阀的响应时间，需要择优选择线圈匝数和驱动电压、驱动电流的搭配。

3 数值计算

电磁阀计算模型采用三维模型，首先对电磁阀原模型进行电磁力的测试，及TIP（电磁阀通电到阀杆完全关闭的时间）实验测试。然后通过三维静态磁场和三维瞬态磁场仿真分别得到电磁阀原模型的电磁力和TIP值，与实验测试进行对比，验证仿真计算的可靠性。最后通过不同线圈匝数与不同驱动电流组合下的静态磁场计算以及不同线圈匝数与不同驱动电压组合下的三维瞬态磁场计算，对比选取出最优的线圈匝数、驱动电流和驱动电压值。

3.1 几何建模及参数设置

电磁阀静态仿真情况下，需要建立内铁芯、铁芯座、线圈、衔铁，计算域，衔铁与内铁芯之间有一定气隙。静态磁场仿真采用电流激励，设置安匝数。瞬态仿真时在静态模型的基础上构建一个多边形棱柱空气包，包住运动件衔铁，空气包外用一个多边形棱柱band包住整个运动区域。band属性中选择参考坐标，设置运动件的运动行程、运动件质量（包括衔铁、衔铁螺钉、阀杆、弹簧、弹簧座）、液压阻尼（通过实验与仿真结合进行调整确定）和弹簧力（随运动件运动位置的改变，力大小变动）。激励源采用电压激励，设置电感、电阻、电压值和线圈匝数。为节省计算时间，计算迭代时间根据现有电磁阀的响应时间确定为700 μs，迭代步长设置为0.5 μs。计算模型如图2所示。

3.2 计算验证

实验测得电磁铁的相关参数如表1所示。

静态磁场仿真计算可知：不同网格数下得到电磁力基本变化不大，所以为了节省计算时间选择网格数较少的情况。得到电磁力F=1得到51.529 6 N，与实验值误差为（151.529 6-145.4）/151.529 6=4.05%。

动态磁场仿真计算可知：采用静态磁场计算中的网格，通过调整damping值使得TIP与实验结果对应。当damping值为230时，得到TIP值为569 μs，与实验值563 μs的误差为1%，计算值可取。

通过以上验证表明，采用本文仿真计算方法及参数设置进行研究可靠。

3.3 计算结果与分析

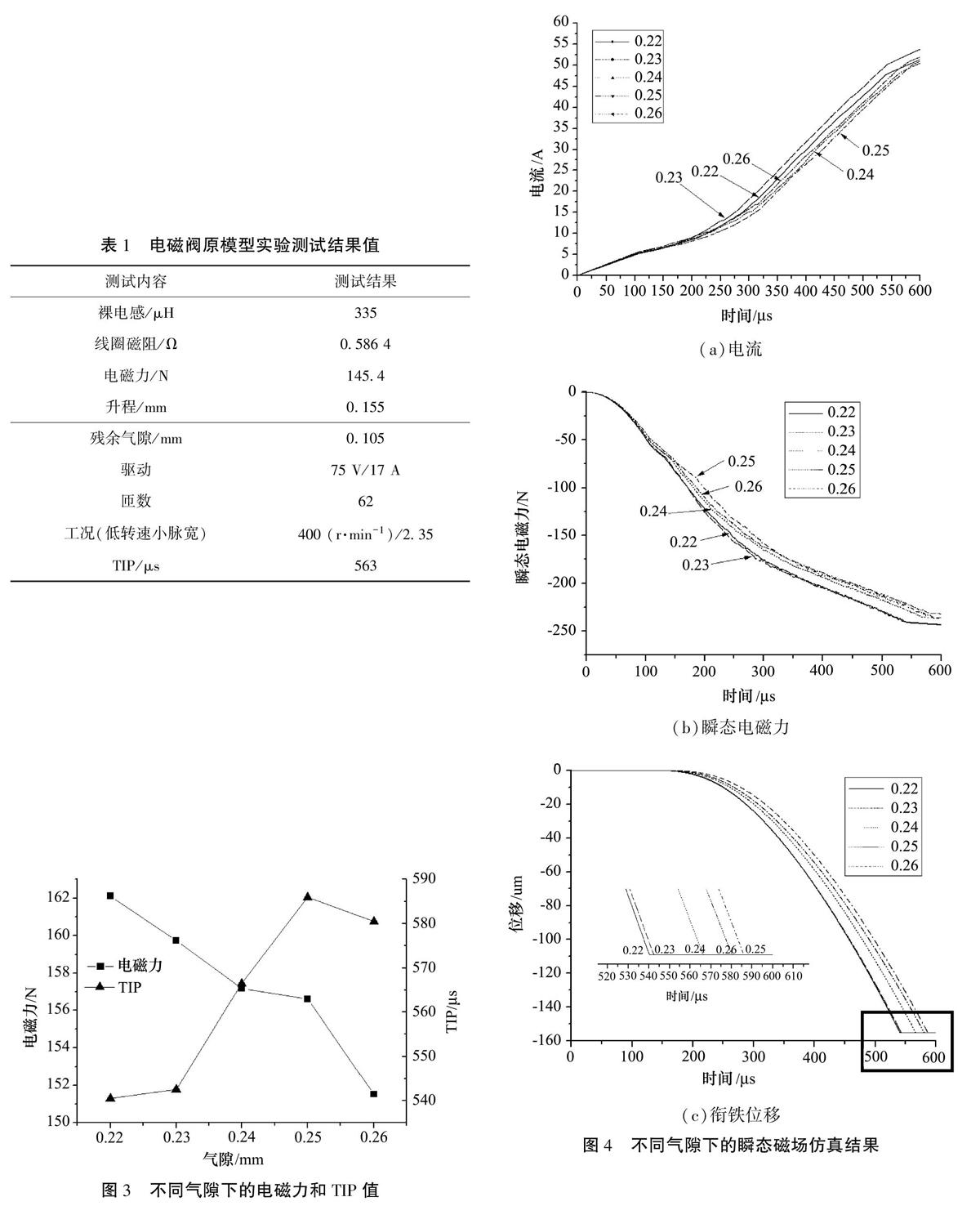
3.3.1 不同气隙下的电磁力和TIP

由图3可见，电磁力呈现随气隙的增大而减小趋势，与理论情况相符。电磁力越大，能克服弹簧力运动的加速度越大，电磁阀关闭时间越短，可见电磁阀气隙越小对电磁阀的响应越有利。

由图4可知，不同工作气隙下，电流、电磁力及衔铁位移都呈现不同的变化趋势。相比之下，气隙越大，电流上升的趋势越缓慢，电磁力下降的趋势越缓慢，衔铁移动越缓慢。

根据不同气隙下的静态仿真和动态仿真可以得到，气隙在0.22、0.23 mm情况下电磁阀关闭响应时间最短。

3.3.2 不同匝数对应不同驱动电流下的静态磁场仿真

在静态电磁仿真情况下，设置不同的匝数和电流（安匝数）进行计算得到，不同匝数对应不同驱动电流下的电磁力。匝数固定，将电流值参数化，10～30 A 步长 2 A，进而设置不同的安匝數，计算得到不同匝数下，电流与电磁力之间的关系，结果如图5所示。

由图5可见，随着匝数的增加，电磁力减小;随着电流的增加，电磁力在减小。当匝数为59、60、75时，在高驱动电流情况下出现电磁力的波动。因此从静态电磁力考虑下，选择匝数为65匝最佳，75、80匝情况次之。电流值可选择小于20 A，这种情况下不仅可以提高电磁力，同时可以减小电流引起的温升。

3.3.3 不同匝数对应不同驱动电压下的瞬态磁场仿真

在瞬态仿真情况下，设置不同匝数和驱动电压进行计算，得到电磁阀的关闭时间TIP。匝数固定设置，将电压值参数化设置，75～80 V步长1 V，计算得到不同线圈匝数下，电压值与时间的关系。

由图6可见，随着电压值的增大，电磁阀动态响应时间缩短，但是随着电压值的增大，缩短时间在减小。由图6可知，当电压值达到78 V时，响应时间减小值小于3 μs，这时驱动电压值已经达到饱和，若继续增大电压，对电磁阀的响应特性帮助很小，同时会大幅增加电压负荷，温度会剧烈上升，因此选择驱动电压值时可以选择在78 V以内。

在满足电磁阀结构条件下，线圈匝数可以选择在50匝，此时电磁阀的响应时间最短。

4 优化结果对比分析

根据以上计算结果得到，电磁阀气隙可以选择0.22、0.23 mm，电磁阀的匝数可以选择50匝，驱动电流20 A，驱动电压78 V。对优选出的结果参数进行计算分析得到结果如表3所示。

两种情况下的响应时间都比原电磁阀响应时间（563 μs）缩短。相比之下，气隙为0.22 mm时，响应时间缩短更多。因此，电磁阀结构参数可以选择匝数为50匝、气隙为0.22 mm，驱动参数可以选择20 A、78 V。

5 结论

1）气隙越大，电流上升的趋势越缓慢，电磁力下降的趋势越缓慢，衔铁移动越缓慢。气隙在0.22、0.23 mm情况下电磁阀关闭响应时间最短。

2）电磁阀结构参数可以选择匝数为50匝、气隙为0.22 mm，驱动参数可以选择20 A、78 V。

3）通过计算分析选出了合适的匝数、电流和电压值的匹配关系，提高电磁阀的响应特性，进而得到稳定的喷油量。对解决目前燃油喷射系统在低转速小脉宽情况下出现供油不稳定的问题具有实际的工程意义。

参考文献：

[1]刘鹏，范立云，周伟，等.永磁并联磁路高速电磁铁的静态特性[J].内燃机学报，2016，（34）5：447-455.

[2]HERFATMANESH M R，LU P，ATTAR M A，et al.Experimental investigation into the effects of two-stage injection on fuel injection quantity，combustion and emissions in a high-speed optical common rail diesel engine[J].Fuel，2013（109）：137-147.

[3]FAN L Y，TIAN B Q，YAO C，et al.A study on cycle fuel injection quantity variation for a diesel engine combination electronic unit pump system[J].Proceedings of the Institution of Mechanical Engineers，Part A：Journal of Power and Energy，2012，226（5）：712-723.

[4]CHENG Q，ZHANG Z D，XIE N L.Power losses and dynamics reponse analysis of ultra-high speed solenoid injector within different driven strategies[J].Applied Thermal Engineering，2015（91）：611-621.

[5]TSAI W C，YU P C.Design of the electrical drive for the highpressure GDI injector in a 500 cc motorbike engine[J].Int.J.Eng.Ind，2011，2 （1）：70-84.

[6]WATANABE H，ICHISE S，NAGAOKA T，Development of compactand high performance fuel injector using electromagnetic field simulation [C]//SAE Paper，2005.

[7]袁海軍.基于Ansoft Maxwell 仿真的电磁阀关闭过程动态特性研究[J].机电产品开发与创新，2011，5（24）：82-84.

[8]徐建中.基于Maxwell 的电磁阀仿真分析[J].造船技术，2015（1）：97-100.

[9]吴萌，熊庆辉，王浚哲，等.电磁阀开启过程动态响应特性有限元仿真研究[J].长春理工大学学报（自然科学版），2015，2（38）：117-120.

[10]辛瑞昊，熊庆辉，王浚哲，等.基Maxwell 的电磁阀仿真与分析[J].长春理工大学学报（自然科学版），2015，2（38）：113-116.

[11]夏胜枝，周明，李希浩，等.高速强力电磁阀的动态响应特性[J].清华大学学报（自然科学版），2002，2（42）：258-261，277.

[12]郝守刚，周明，夏胜枝，等.电控单体泵电磁阀动态响应特性数值仿真[J].内燃机工程，2003，3（24）：10-13.

[13]李春青，姜峰，李明海，等.高速电磁阀动态响应特性的仿真分析[J].计算机仿真，2013，11（30）：224-227.

[14]欧阳光耀，安世杰，刘振明，等.柴油机高压共轨喷射技术[M].北京：国防工业出版社，2012.