基于PCA的高维流式数据聚类算法

张云龙

摘要：本文的基于PCA的高维流式数据聚类算法是在D-Stream算法的基础上提出来的。首先，从基本原理上分析了D-Stream算法在高维网格划分时，存在着大量计算，影响算法效率;其次，对于高维数据本身而言，存在着数据高维稀疏的特性;最后，本文采.用PCA降维与滑动窗口技术相结合的思想来改进D-Stream算法，并通过仿真实验证明了算法的可行性。

[关键词]流式数据PCA滑动窗口聚类

1引言

近年来，我们处在一个数据爆炸式增长的时代，从以往的静态数据过渡到流式数据，其隐藏在这些数据背后的商业价值是不可估量的。如今，在有限的计算能力下处理流式数据处处受限，导致流式数据聚类算法的运行效率受到一定的影响，如何提高流式数据聚类的效率尤其是针对高维数据尤为重要。

2007年由chen提出的基于网格密度的D-Sream算法，处理的是一个个网格，而非一个个数据，所以算法具有一定的速度优势。但是在网格划分时，D-Stream存在高维网格划分需要计算消耗，所以影响算法的运行效率。近年来，对于网格密度的算法也有着大量的研究，例如：孙玉芬针对高维数据问题提出的基于聚类子空间的GSCDS算法、于翔等人提出的数据子空间的SC-RP算法、刘波等人提出的属性最大间隔的子空间聚类算法MMSC、肖红光等人于2016年提出的基于结构树的高维流式数据子空间的自适应聚类算法等。针对以上众多算法研究发现，针对高维数据流的算法大都采用映射子空间的技术来解决，但是算法需要预先设定参数，且计算量有所增加，消耗一定的内存。而且未针对高维数据稀疏问题作出分析。在有限的计算资源下，提高高维流式数据聚类算法的效率具有一定的研究意义。

2 一种新的基于网格密度的流式数据聚类算法

2.1PCA数据降维算法原理简介

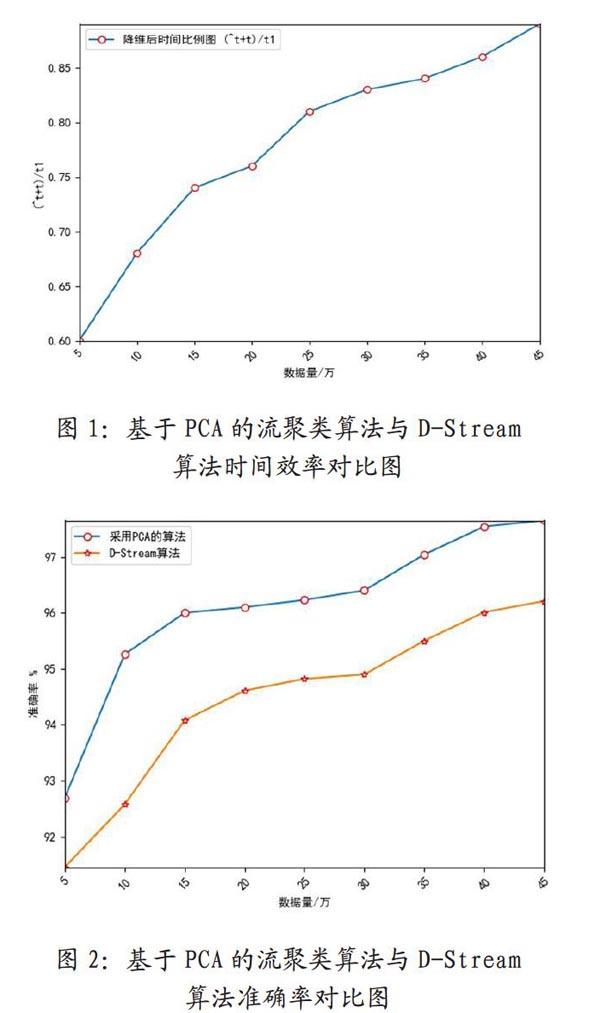
PCA降维算法基本原理：主成分分析的的主要思想是将n维特征映射到k维上（k

（1）标准化模块;

（2）相关矩阵模块的计算;

（3）特征值特征向量的求解;

（4）主成分的保留。

其中，主成分分析法可以最大程度的保留原始数据的信息，所以可以提供足够的的信息来综合反映原始数据。

2.2PCA与滑动窗口技术结合实现数据流降维

本文认真分析了D-Stream在划分网格是存在的高维问题，以及高维数据本身的稀疏性特点，最终选择了比较成熟的PCA降维算法，主成分分析顾名思义可以保留数据尽可能多的完整性，并且在针对高维数据稀疏上有一定的处理能力。

但是主成分分析并不能直接处理流式数据，这是由流式数据特点决定的。数据流式具有快速的、大量的、持续不断产生的特点，所以本文分析并使用滑动窗口技术与PCA算法相结合来适应流式數据的处理。其中，采用定滑动窗口模式，为滑动窗口定一个值，并采用周期法，数据流流入时，且数据片段未达到窗口大小时，暂时将数据存储在缓存区内，当满足滑动窗口要求时将数据放入滑动窗口内，对数据进行降维处理。当数据开始流入算法时，设滑动窗口大小为γ，然后判断流入的数据是否达到滑动窗口的大小，若是没有则继续流入数据，当达到滑动窗口大小时，使用PCA降维处理窗口内的数据。当选取了尽可能优的低维空间，得到了降维后的数据集，对降维后的数据再进行极差标准化处理，然后再进行数据的摘要提取和网格划分。

2.3基于PCA的高维流式数据聚类算法的实现

本文采用的是滑动窗口与PCA结合的思想对其进行降维处理，然后再对滑动窗口中处理后的数据进行摘要的提取，网格的划分，在时间间隔gap后，离线过程根据网格的密度以及一些判断条件对网格进行处理，包括更新网格密度、删除零星网格等，最后再根据DBSCAN算法对网格进行密度聚类，形成一个个的簇，并且在离线过程对簇进行调整，包括簇的合并、簇的分裂等。其中的主要的过程如下：

输入：数据流X、网格密度系数入、时间t、参数β、C、Cm网格划分r输出：聚类簇

（1）Algorithmbegin

（2）t=0

（3）Whiledatacollectionforeachslidingwindow#在满足滑动窗口大小时

（4）Receive（X）

（5）PCAdimensionreductiongenerationmatrixX#使用PCA降维得到数据

（6）RangestandardizationX'

（7）FordatainX'#将数据输入到后续的处理算法中

（8）t.+=1

（9）BasedonrDividingGrid

（10）ForeachdataX;#新数据点加入

（11）Joingridgandupdate#新数据加入以及网格更新

（12）Ift。%gap=0

（13）JudgeandremoveSporadic

（14）UpdateAllGridbasedonλ

（15）UseDBSCANclusteringgrid

（16）endAlgorithm

上述步骤是基于PCA的高维流式数据聚类算法的简要处理过程，算法采用的滑动窗口技术与PCA降维算法相结合的特点，符合流式数据处理的条件，并且在降低高维数据的难题下，PCA算法又可以很大程度上的保留原始数据的完整性，并且在降维的过程中又可以在一定程度，上消除数据的高维稀疏特性，不仅降低了数据处理的计算量，提高了聚类的效率，而且在算法的处理上有着一定的好处，可以保证聚类的质量。

3算法的实验结果及分析

本节对基于PCA的流式数据聚类算法进行性能测试，实验平台的配置如下：操作系统：Win7_64位;CPU为i5处理器;开发平台：pycharm。实验数据集采用的是网络入侵检测数据集KDDCPU99。实验使用数据集模拟数据流进行输入，其中算法参数λ=0.998，β=0.5，窗口的大小设置为5万（一个窗口中的数据量达到五万）。

从原理上来分析，基于PCA的高维流式数据聚类算法降低了数据的特征维度，并且一定程度上解决了数据高维稀疏的特点，所以大大的减少了网格划分时所产生的计算量，从而改善了算法的运行效率，图1即为本文提出的算法与D-Stream算法在网络入侵数据集上的运行效率对比图，其中^t代表PCA降维的时间，t表示降维后数据聚类的时间，t表示原始D-Stream算法运行的时间，设

来表示算法运行效率的对比度，如图1所示。

从图1的运行结果可以看出，本文提出的基于PCA的高维流式数据聚类算法明显的比D-Stream算法在聚类效率上有所提高。本文提出的算法具有明显的优势，首先，该算法采用了滑动窗口技术，使得处理的数据可以分批次批量处理;其次，从直接处理高维数据，变成处理极大保留了原始数据完整性的低维数据，使得网格划分产生的计算量大大的降低，从而使得算法的运行效率得到大大的提高。

针对高维数据的高维稀疏性的特点，实验之前，分析了实验数据集，发现该数据集不仅存在高维特性，而且出现数据稀疏的特点，所以又做了本论文提出的基于PCA的高维流式数据聚类算法与D-Stream算法的准确率对比，实验结果图如图2。

由上述实验的数据结果得出，本论文提出的基于PCA的高维流式数据聚类算法，在一定程度上可以处理高维流式数据，在对高维数据存在的数据稀疏的问题上具有一定的去噪能力，由实验结果表明本文提出的基于PCA的高维流式数据聚类算法较D-Stream算法在聚类精度上有一定的提高。

4总结

本文提出的基于PCA的高维流式数据聚类算法是基于D-Stream算法的基础上进行改进，该算法能有效的处理高维数据，并且基于密度的聚类可以发现任意形状分布的簇，实验结果表明该算法的可行性，不仅提高了效率，而且在一定程度上解决高维稀疏的特性，提高聚类准确率。对于未来的研究，将放在进一步提高算法的效率与准确率上，自适应算法的加入是下一步研究重点。

参考文献

[1] Chen Y， Tu L. Dens i ty-BasedClustering for Real-Time StreamData. KDD07， August12-15， 2007， SanJose， California， USA.133-142.

[2]孙玉芬，基于网格方法的聚类算法研究[D].华中科技大学，2006.

[3]于翔，印桂生，许宪东等.一种基于区域划分的数据流子空间聚类方法[J].計算机研究与发展，2014，51（01）：88-95.

[4]刘波，王红军，成聪等，基于属性最大间隔的子空间聚类[J].南京大学学报（自然科学），2014，50（04）：482-493.

[5]肖红光，陈颖慧，巫小蓉，基于结构树的高维数据流子空间自适应聚类算法[J].小型微型计算机系统，2016，37（10）：2206-221.