大厚度复合材料层合板的固化温度场变化规律

(1．沈阳航空航天大学 航空制造工艺数字化国防重点学科实验室，辽宁 沈阳 110136；2．西北工业大学 机电学院，陕西 西安 710072)

1 引 言

先进树脂基复合材料具有可设计性强、密度小、比强度高、耐腐蚀、耐疲劳等优异性能，在航空领域得到了广泛应用。在工业生产中，产品的最终尺寸精度必须满足生产要求，但在加工成形的过程中，复合材料的热传导以及化学反应会使构件内部温度呈梯度分布，导致构件内部产生大量残余应力，从而诱发产品变形。因此，对复合材料成形固化过程中的温度场分布的研究尤为重要。

随着厚截面复合材料的大量应用，其制造难度也逐渐受到关注，国内外大量学者对其固化过程中出现的固化不均匀[1-9]，温度过热[1-11]，制造时间长等问题展开了研究。龙祥等[12]通过三种不同方式使复合材料固化，观察固化过程中的温度变化情况。Pantelelis 等[13]建立了一维复合材料非线性有限元分析模型，得到了复合材料层合板的温度变化规律。Loos等[14]建立了AS4/3501-6的一维有限元分析模型，分析并得到了固化温度变化历程与固化度、温度以及树脂流动等的关系。Bogetti和Giliespie[15]建立了复合材料的二维热传导模型，通过固化动力学耦合模型研究了厚截面层合板任意截面固化度和温度的发展历程。以上学者建立的模型均为一维或者二维，无法考虑材料整体厚度方向上的温度变化，对研究大厚度复合材料厚度对固化的影响有一定局限性。而谭华等[16]采用三维模型模拟了大型复杂的复合材料结构内部的热传导现象，并得到其内部温度场的分布情况。郭战胜[17]等研究了厚截面树脂基复合材料制造过程中的内部温度场发展变化，开发了可以模拟复合材料整个制造过程中复杂物理化学变化软件，发现现有的一般厚度复合材料的固化历程不适合固化厚截面复合材料。

本研究在确定固化方式的基础上，进一步分析了厚度对复合材料固化变形的影响，通过建立三维有限元模型，以ABAQUS为依托，通过编写ABAQUS子程序，将固化反应动力学方程引入热传导方程，研究大厚度玻璃纤维/环氧树脂复合材料固化过程中温度分布规律，更准确地对大厚度复合材料层合板的固化过程进行了模拟，进一步分析了大厚度复合材料固化过程温度场在厚度方向上的差异，为大厚度复合材料固化选择合适的固化温度周期提供了参考，对实际生产具有指导意义。

2 数学模型

2.1 热化学模型

热固性树脂基复合材料的固化过程本质是热传导系数较低、各向异性具有非线性内热源的化学反应过程，其中的内热源指的是树脂基体发生固化反应放出的热量。目前的热化学模型都是由傅里叶热传导定律与固化动力学方程得出[18]：

(1)

式中：ρc为复合材料密度，Cpc为复合材料比热，kii为复合材料各向异性的热传导系数，ρr为树脂密度，Hr为固化反应放出的总热量，α为固化度，T为温度，t为时间，vr为树脂体积分数。

复合材料的密度、比热通过混合率计算得到：

ρc=Vfρf+(1-Vf)ρr

(2)

Cpc=(1-Wf)Cpr+WfCpf

(3)

其中：Vf、Wf分别为复合材料中纤维的体积分数和质量分数；ρf、ρr分别为纤维与树脂的密度；Cpc、Cpr、Cpf分别为复合材料、树脂以及纤维的比热。

复合材料的热传导系数是各向异性的。复合材料平行于纤维方向的热传导系数用混合率得到：

K//=Kr(1-Vf)+KfVf

(4)

其中K//、Kr、Kf分别为复合材料平行纤维方向的热传导系数和树脂以及纤维的热传导系数。

垂直于纤维方向的热传导系数使用模型预测。不同的模型预测的结果也不同，本研究使用Springer-Tsai模型[14-15]：

(5)

(6)

其中：K┴为复合材料垂直于纤维方向的热传导系数。

2.2 固化动力学模型

不同的树脂体系，固化反应机理不同，众多学者根据不同树脂得到不同种类的固化动力学模型。Kissinger[19]研究n级反应动力学模型，其特点是从固化一开始，反应速率就达到最大值，随着固化的进行，逐渐降到零。即：

(7)

(8)

对于自催化模型，存在诱导期，固化速率一开始为零或者很小，逐渐达到最大速率，随着固化过程的进行，逐渐降到零。即：

(9)

(10)

(11)

(12)

不同的复合材料具有不同的反应机理，但对常用的双马树脂基和环氧树脂基复合材料的固化反应符合自催化反应规律，因此选用式(9)及(10)表达。图1为温度场与固化度场耦合求解流程图，固化过程中树脂固化放热通过子程序HETVAL定义热源项实现。

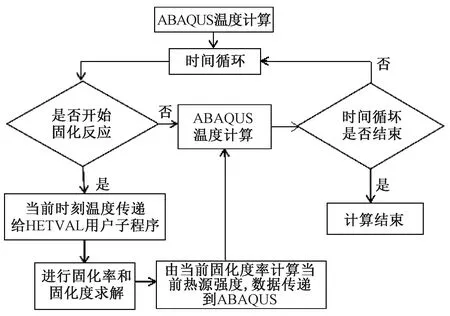
图1 计算流程图Fig.1 Calculation flow chart

3 模拟过程

3.1 验证模型

验证模型采用3234/T300B复合材料层合板，尺寸为100×100×22.8mm，该模型及其材料参数参考文献[20]，建立有限元分析模型如图2。

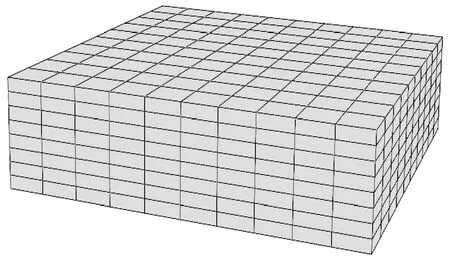
图2 三维有限元分析模型Fig.2 Three dimensional finite element analysis model

选取层合板中心点与已有实验结果[20]进行对比，如图3所示。从图可知，模拟结果与实验结果基本吻合。

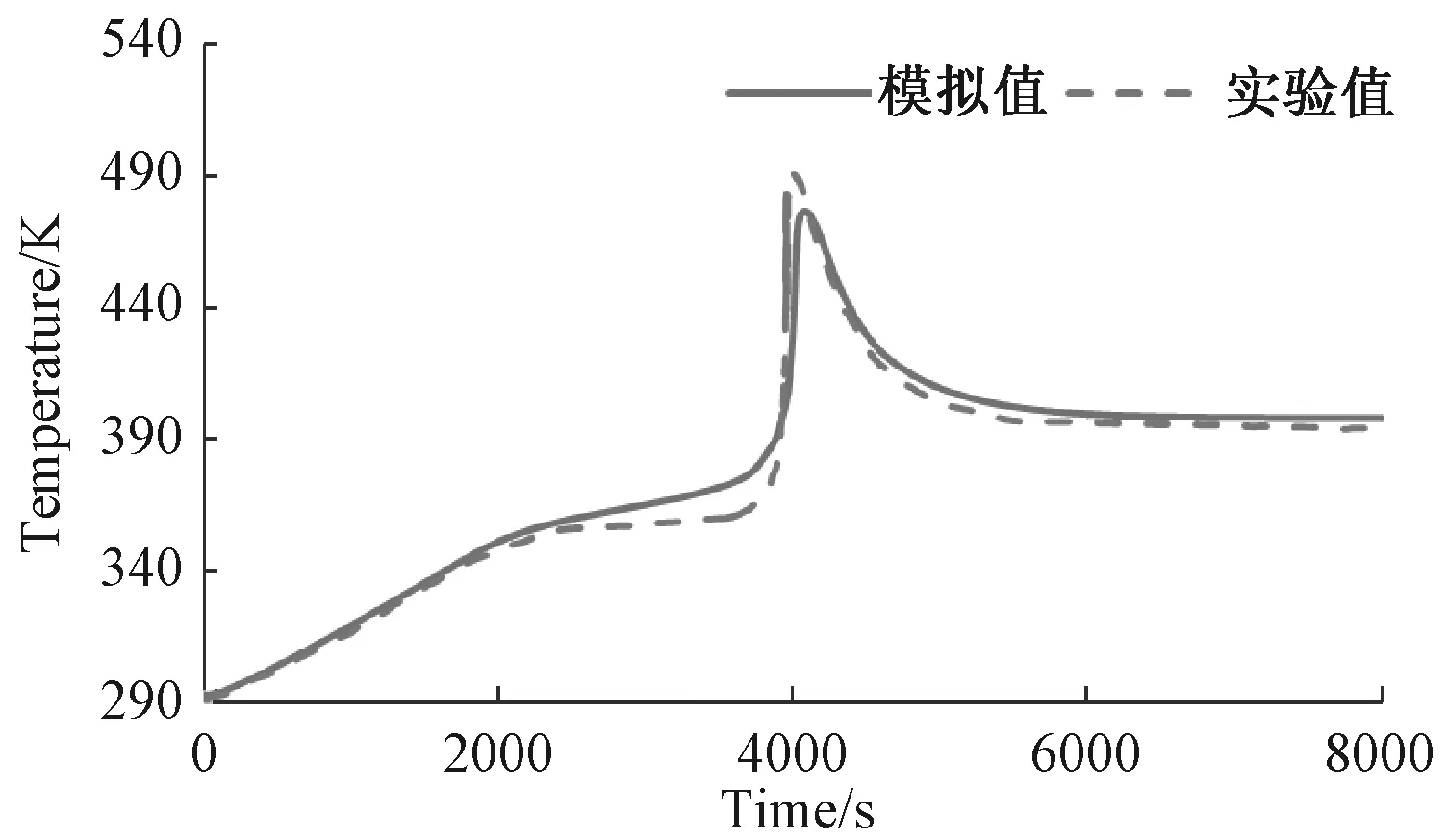
图3 实验与模拟温度曲线图Fig.3 Experiment and simulation temperature curve chart

3.2 实验设计

实验设计为复合材料层合板放置在上下两个用于加热的模具之间，层合板铺层方向一致，铺层角度均为0°。固化开始前，需要一定的升温时间将纤维增强材料预热到初始温度Ti，厚度为40mm的玻璃纤维层合板在升温到稳定状态时复合材料构件内部温差不超过1℃，可以认为层合板内部初始温度是均匀的。本文的模拟中，假设时间t=0时，复合材料构件已预加热到固化温度Tc，即Ti=Tc。本研究只研究固化开始到结束的过程的温度与固化度分布情况，忽略升温与降温冷却阶段。因为上下表面边界条件相同，且四周为绝缘壁面，所以复合材料构件的温度分布只在厚度方向上有所变化，在平面范围内是均匀的。因此重点研究厚度方向的温度与固化度分布情况。

为着重研究复合材料固化过程中厚度方向的温度最大变化量与厚度和固化温度的关系，对有限元模拟进行了以下假设：复合材料的初始温度均匀且与固化温度相同；复合材料上下表面边界条件为恒温且与固化温度相同；固化过程中，复合材料物理性能参数不变。

图4给出了复合材料层合板模型及其边界条件，其尺寸为长a=200mm，宽b=200mm，厚度c=40mm，模拟时用到的各种参数见表1与表2，参考了文献[21]中的数据，其中树脂体积分数为44%。

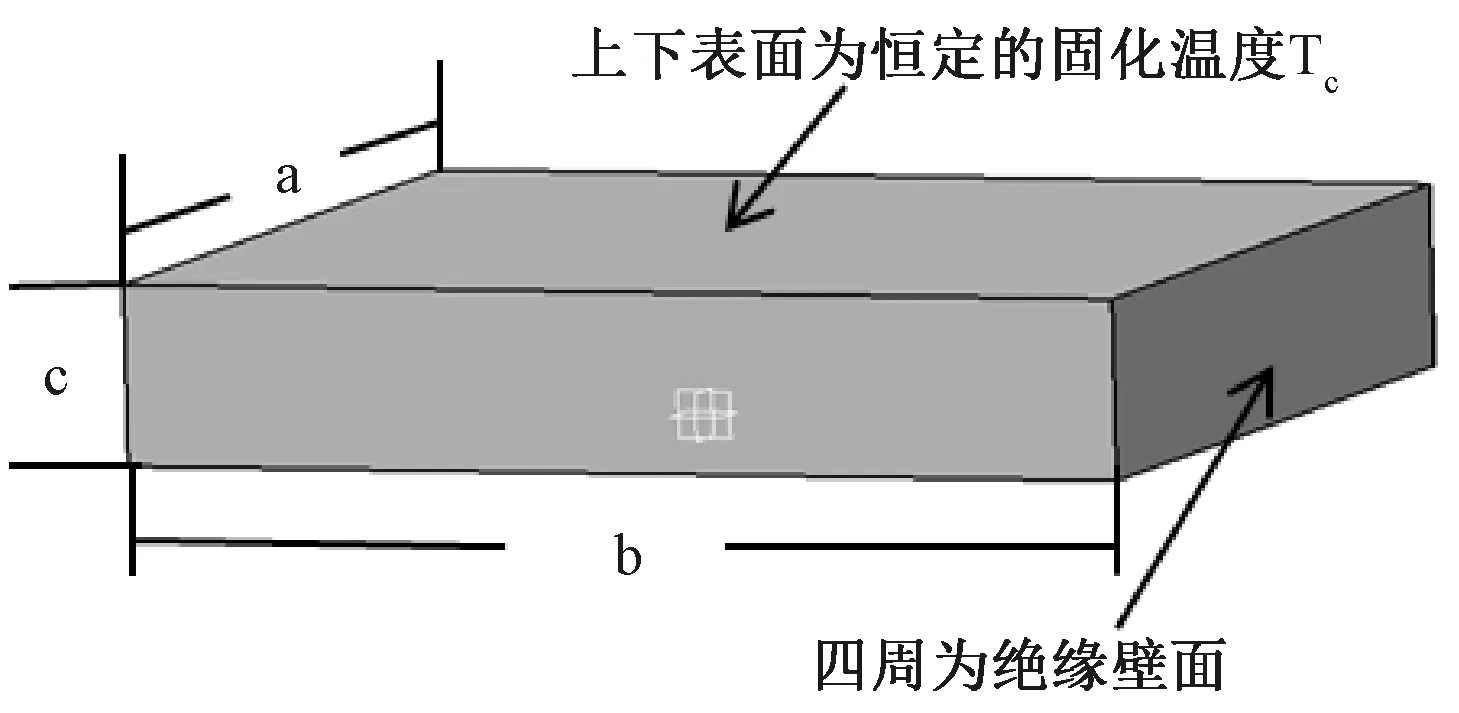
图4 层合板几何尺寸与边界条件Fig.4 Laminated plate geometric size and boundary conditions

表1 复合材料固化动力学参数Table 1 Composite curing kinetic parameters

Note:A1and A2are the frequency factors of the autocatalytic model,m and n are the reaction orders of the autocatalytic model,and Ea1and Ea2are the activation energies of the autocatalytic model.

表2 复合材料热学参数Table 2 Composite material thermal parameters

Note:ρcis the composite density,Cpcis the specific heat of the composite,and Kiiis the thermal conductivity of the composite anisotropy

4 模拟结果与讨论

4.1 层合板厚度方向上温度、固化速率、固化度的分布

图5是固化温度为90℃时构件在厚度方向距离中心点不同位置的温度随时间变化的曲线示意图。复合材料构件尺寸为200×200×40mm，图中0mm表示复合材料构件中心点的温度，20mm表示距离复合材料中心点20mm处的温度，即上下表面的温度。本模拟研究中层合板上下表面温度相同具有对称性，所以结论中只给出了层合板一半的相关曲线。固化过程中产生大量热量，中心点生成的热量不能够及时扩散，造成温度急剧升高，750s时中心点温度达到最大值140.3℃，升温幅度达50.3℃。构件表面与温度恒定的模具表面接触因而温度不变，厚度方向的温度随着距离中心点位置的增大而降低，随着固化的完成，复合材料构件内温度逐渐降低到初始温度。

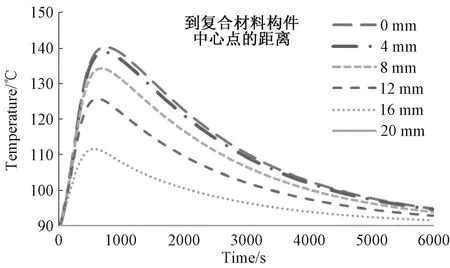
图5 构件厚度方向不同位置的温度随时间变化曲线Fig.5 Curves of temperature changing with time in different locations along thickness

图6为构件厚度方向不同位置的固化速率。厚度方向上的固化速率受温度分布的影响，越靠近中心点，温度越高，固化速率也越大，在t=260s时，中心点的固化速率达到最大值0.2060×10-2，此时中心点的温度仍在升高，在t=750s时，固化速率降到0.2594×10-3，此时温度达到峰值140.3℃。此现象表明在固化速率降低到0.2594×10-3之前，固化产生热量的速率大于热传递传出热量的速率；当固化速率降到0.2594×10-2之后，固化产生热量的速率小于热传递传出热量的速率，温度开始降低。作用在表面的恒定温度载荷使表面的温度保持不变，与中心点相比，固化速率处于相对较低、平稳的状态。

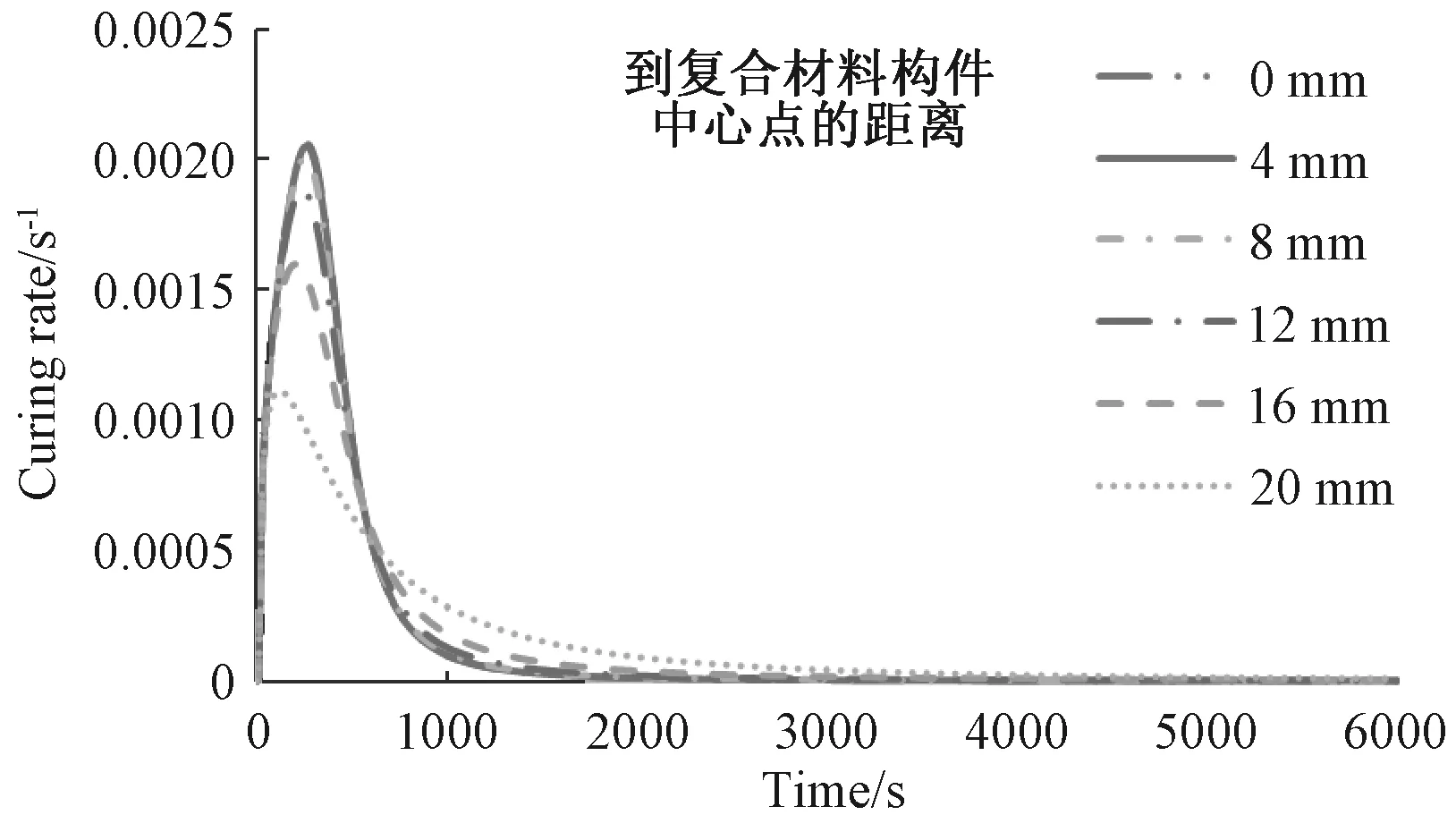
图6 构件厚度方向不同位置的固化速率随时间变化曲线Fig.6 Curves of curing rate changing with time in different location along thickness

图7为构件厚度方向不同位置的固化度随时间变化曲线。固化开始阶段，中心点的固化速率急剧升高，750s时中心点的固化度达0.90，而表面位置的固化度只有0.57；中心点固化度在2170s时已达到0.98，到t=6000s时仅上升了0.01左右，而表面固化度在6000s时也达到0.95，这说明固化反应放出的热量能够提高固化度。

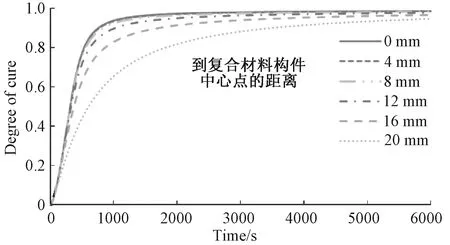
图7 构件厚度方向不同位置的固化度随时间变化曲线Fig.7 Curves of curing degree changing with time in different location along thickness

4.2 构件厚度和固化温度对固化度场及温度场分布的影响

为了研究复合材料厚度与固化温度对固化度场与温度场分布的影响，做了两组算例。第一组固化温度保持90℃不变，复合材料构件厚度从20mm到45mm；第二组厚度保持40mm不变，固化温度分别为60，70，80、90和100℃。

如图8所示，固化温度恒定为90℃时，复合材料构件越厚，构件中心点温度峰值越高，降温到初始温度所需要的时间越长。其中当复合材料构件厚度小于40mm时，在t=6000s时刻厚度方向温度分度已基本恢复均匀；当复合材料构件厚度大于40mm时，在t=6000s时构件中心点的温度仍然较高于表面。

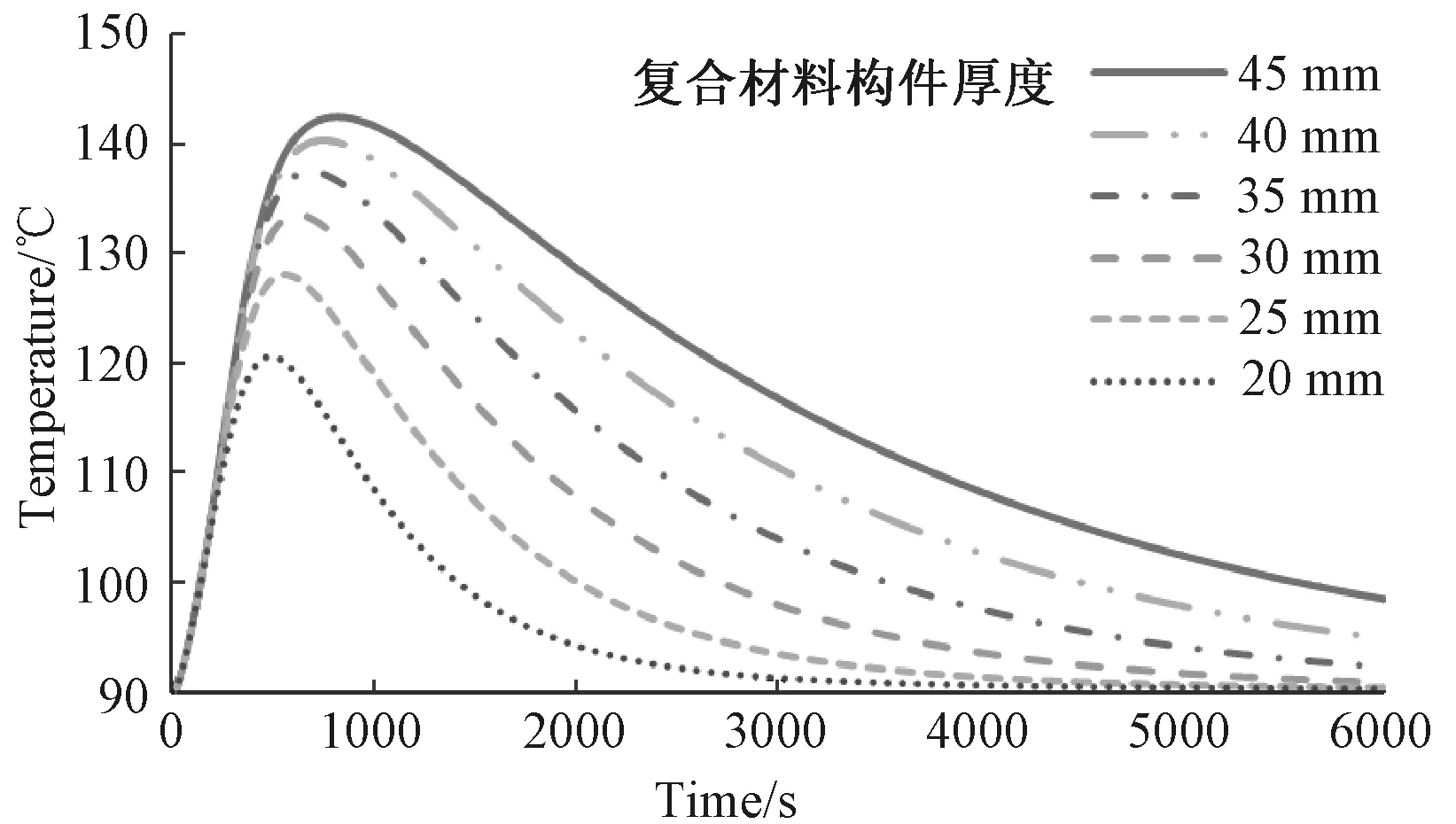
图8 不同厚度复合材料中心点温度随时间变化的曲线Fig.8 Center temperature change curve over time in different location along thickness

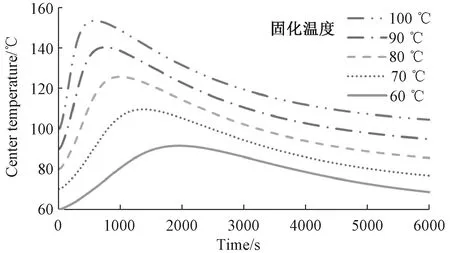
图9 不同固化温度时复合材料中心点温度随时间变化的曲线Fig.9 Curves of center temperature change over time in different location along thickness

图9为厚度40mm的复合材料构件固化温度分别为100，90，80，70和60℃时，中心点的温度分布曲线。固化温度越低，固化速率越低，升温速率越低，并且复合材料构件中心点的最高温度也越低。

4.3 构件厚度与温度对不同时刻温度差值的影响

定义Tmax为复合材料内部中心点温度峰值，T6000为t=6000s时的中心点温度。最大温差ΔTmax为中心点温度峰值与固化温度Tc的差值，ΔT6000为t=6000s时中心点温度与固化温度Tc的差值。

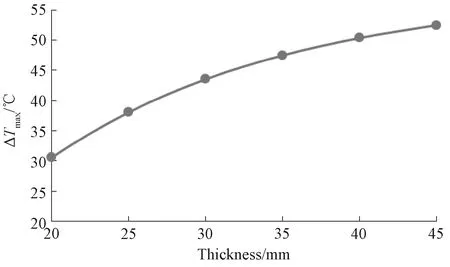
图10 不同厚度复合材料中心点温度最大差值Fig.10 Maximum center temperature difference at different thickness of composite materials

图10为不同厚度复合材料中心点的最大温差值，最大温差ΔTmax随着厚度的增加而增大，随着厚度的增加，最大温差增大的趋势逐渐减小，复合材料层合板厚度足够大时，厚度对中心点最大温差值的影响趋于一致。厚度为20mm构件的温度峰值比固化温度大33.3%左右，当厚度增大到45mm时，温度峰值比固化温度大58.3%左右。

图11所示为不同固化温度时复合材料中心点最大温差值。最大温差ΔTmax随固化温度Tc的升高而增大，随着固化温度的升高，ΔTmax增大程度逐渐降低。固化温度Tc=60℃时，温度峰值比固化温度大52.6%，固化温度为70、80、90和100℃时，温度峰值分别比固化温度大56.5%、57.2%、55.9%和53.5%。

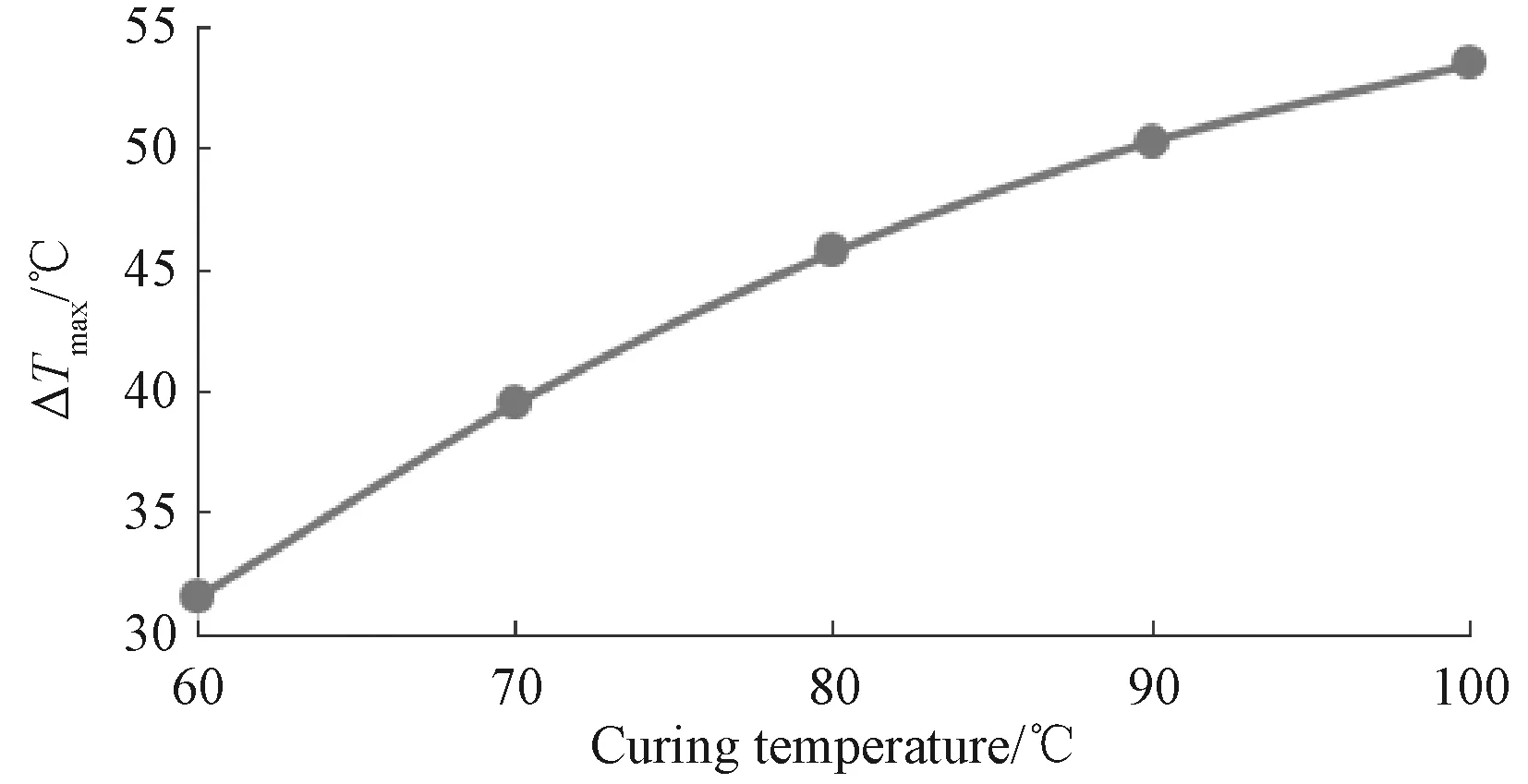
图11 不同固化温度时复合材料中心点温度最大差值Fig.11 Maximum center temperature difference of composite materials with different curing temperature

如图12所示，t=6000s时，复合材料构件中心点的最大温差值随着厚度的增加呈指数增高，厚度小于35cm时，固化结束时的中心点温差值普遍较小；厚度大于35cm时，厚度对固化结束时的中心点温差值影响增大。说明温度一定时，复合材料层合板在一定厚度范围内固化产生的热量可以快速传递，厚度增加到一定程度时，热量传递需要更多的时间。由此说明复合材料构件越厚，需要冷却的时间越久。

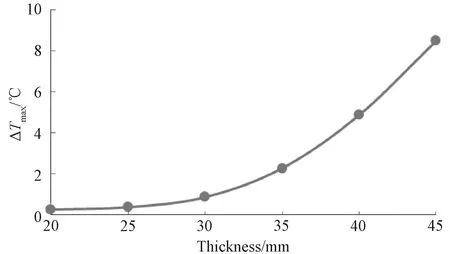
图12 t=6000s时不同厚度复合材料中心点温度差值变化Fig.12 Center temperature difference as t=6000s at different thickness of composite materils

图13为厚度40mm的复合材料构件在固化温度为60，70，80，90和100℃，t=6000s时，中心点温度与固化温度的温差值。可以看出，固化温度过低，固化结束时复合材料中心点温度差值较大，随着固化温度的增加，中心点温度差值逐渐减小。由此说明厚度一定时，固化温度越高，需要的冷却时间越短。

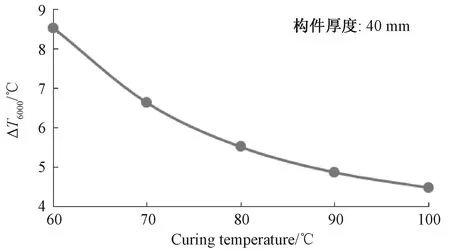
图13 t=6000s时不同固化温度复合材料中心点温度差值变化Fig.13 Center temperature difference when t=6000s with different curing temperature of composite materials

4 结 论

1．固化过程中，越接近复合材料构件的中心，升温幅度越大。温度越高，固化速率越大，固化完成的时间越短。

2．固化温度一定时，复合材料厚度越大，构件中心温度与固化温度之间的最大温差ΔTmax越大，需要恢复到初始温度的时间越长。随着厚度的增加，ΔTmax增大的趋势越小。

3．复合材料厚度一定时，固化工艺温度越高，最大温差ΔTmax越大，需要恢复到初始温度的时间越短。随着厚度的增加，ΔTmax增大的趋势越小。