拉断螺栓式固弹装置动态力学性能对发射内弹道的影响分析

隋九龄，熊文慧，李鹏永，罗 亮

(1. 中国船舶重工集团公司第七一三研究所，河南 郑州 450015；2. 河南省水下智能装备重点实验室，河南 郑州 450015)

0 引 言

在某型战术导弹舰载发射装置中，选用拉断螺栓式固弹装置将导弹固定于发射装置内。导弹发射过程中，弹射动力系统按设计规律产生高温高压燃气，燃气在发射筒中膨胀做功，推动导弹及弹底板运动[1]。一端与发射装置固定一端随弹底板运动的拉断螺栓承受拉力，当拉力超过拉断螺栓的拉断力极限后，拉断螺栓在预定位置断裂，之后导弹弹射出筒。

为准确计算导弹的出筒速度、最大加速度以及弹动时刻等特征参数，必须确定导弹发射过程中拉断螺栓实际的拉断力。

1 拉断螺栓结构

为抵抗导弹在运输及战备值班过程中面临的振动、冲击载荷，总体对固弹装置承受过载的能力提出了定量要求。相比固弹销、爆炸螺栓等形式，拉断螺栓式固弹装置具有结构简单、安全可靠、使用方便等优点。

本文所涉及的拉断螺栓式固弹装置材料选用45号钢，结构及布置形式如图1所示。实际工作中每套导弹发射装置中使用2枚拉断螺栓式固弹装置，间隔180°对称布置，螺栓穿过发射装置上的限位孔后小端螺纹与弹底板拧紧固连，凸台端受限位孔的约束与发射装置固定。导弹发射过程中，燃气推动导弹及弹底板运动，拉断螺栓承受拉力，当拉力超过拉断螺栓的拉断力极限后，拉断螺栓在预定位置断裂，之后导弹弹射出筒。

图1 拉断螺栓结构简图及布置形式Fig. 1 Structural layout of snap-bolt

拉断螺栓完成后，严格按照GB/T228.1-2010《金属材料 拉伸试验 第1部分：室温试验方法》[2]进行了拉断螺栓在室温下的拉断力抽检试验，试验结果如图2及表1所示。

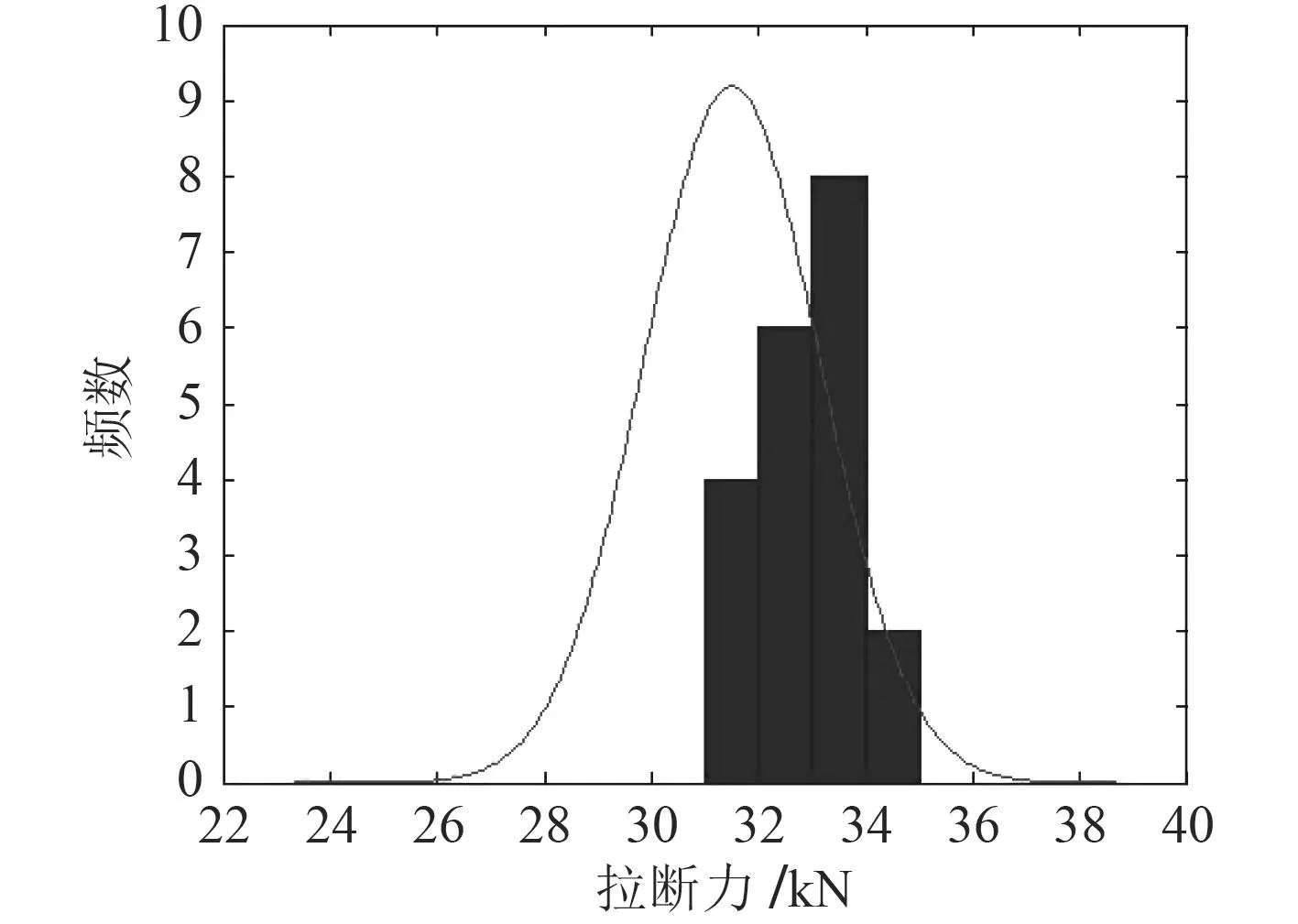
图2 拉断螺栓拉断力检验结果分布规律Fig. 2 Distribution pattern of breaking force test results of snap-bolt

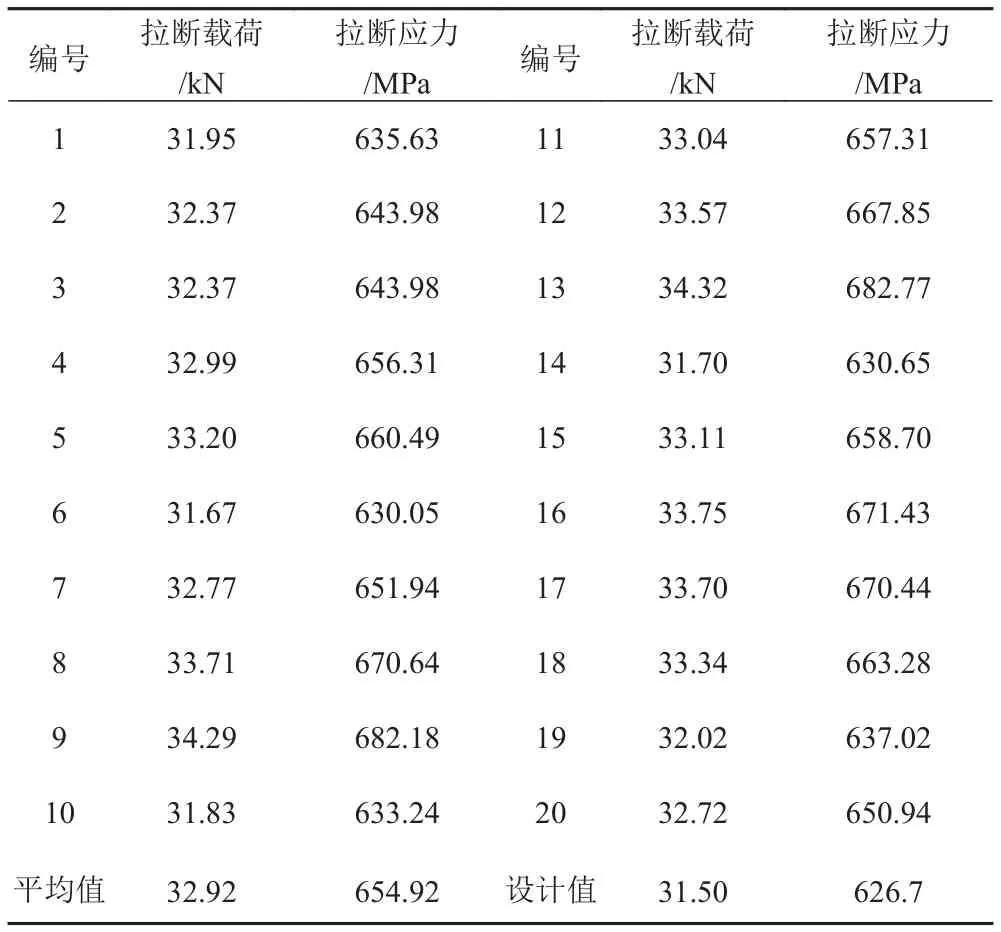
表1 拉断螺栓拉断力检验结果Tab. 1 Breaking force test results of snap-bolt

拉断力抽检试验结果表明，该批拉断螺栓实际的拉断力在 31.67～34.32 kN 之间，满足 31.5±3.15 kN的设计要求，拉断应力则在633.24～682.77 MPa区间内，基本呈正态分布。试验结果的分布呈现偏大的趋势。

但是，拉断力抽检试验中的应力加载速率为6～60 MPa·s–1，而在导弹发射过程中，实际的应力加载速率为 30 000～40 000 MPa·s–1，与抽检试验中的应力加载速率差异极大。因此仍需对导弹发射过程中拉断螺栓式固弹装置的动态力学性能展开进一步的研究。

2 拉断螺栓的非稳态结构仿真

为获取导弹发射过程中拉断螺栓式固弹装置实际的拉断力，基于Autodyn显式动力学求解器对拉断螺栓式固弹装置展开仿真研究。Autodyn是一种通用显示动力学有限元分析程序，特别适合于求解各种高度非线性动力学问题。

建立的拉断螺栓几何模型及网格划分如图3所示。45号钢的材料本构模型与失效模型均选用Johnson-Cook模型，Johnson-Cook模型一般用于描述大应变、高应变率、高温环境下金属材料的强度极限以及失效过程[3]。参考文献[4]，45钢的Johnson-Cook模型中各参数的取值见表2。

图3 拉断螺栓式固弹装置的几何模型及网格划分情况Fig. 3 Geometric model and mesh generation of snap-bolt fixed device

施加的边界条件共两项（见图4）：A为0.03 s内加载于弹底板下表面的压力载荷，B为拉断螺栓凸台处的固定支撑。施加的压力载荷根据试验中实测的0～0.03 s内的压力数据进行线性拟合而得。拟合结果为分段曲线：

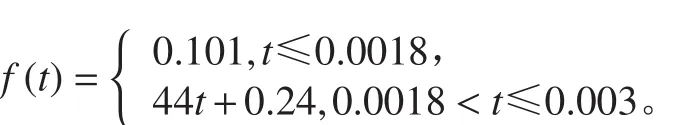
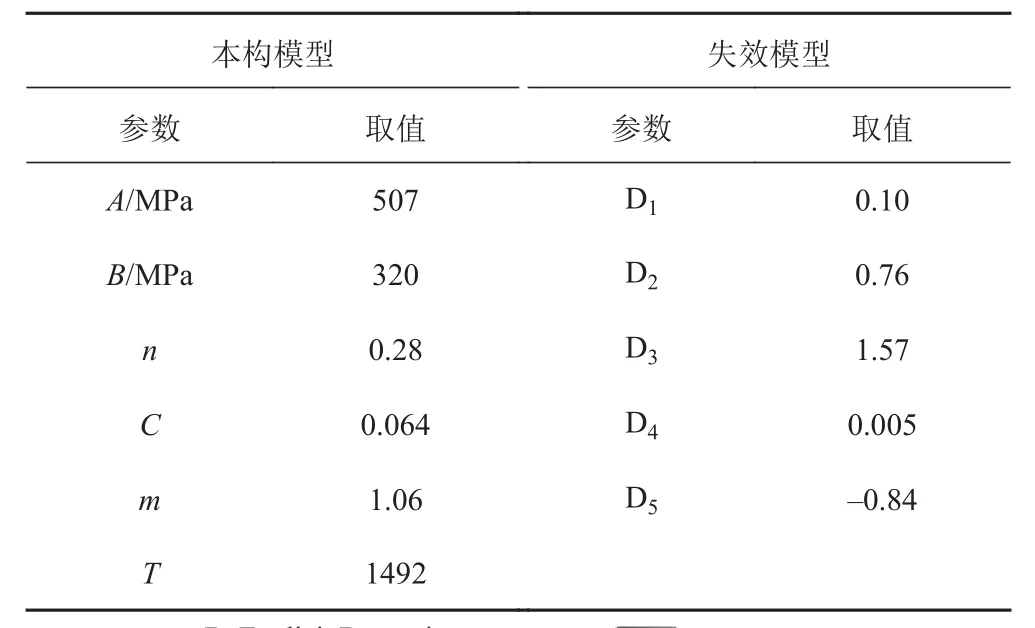
表2 Johnson-Cook本构及失效模型中的参数选取Tab. 2 Parameters and values of Johnson-Cook constitution and failure model

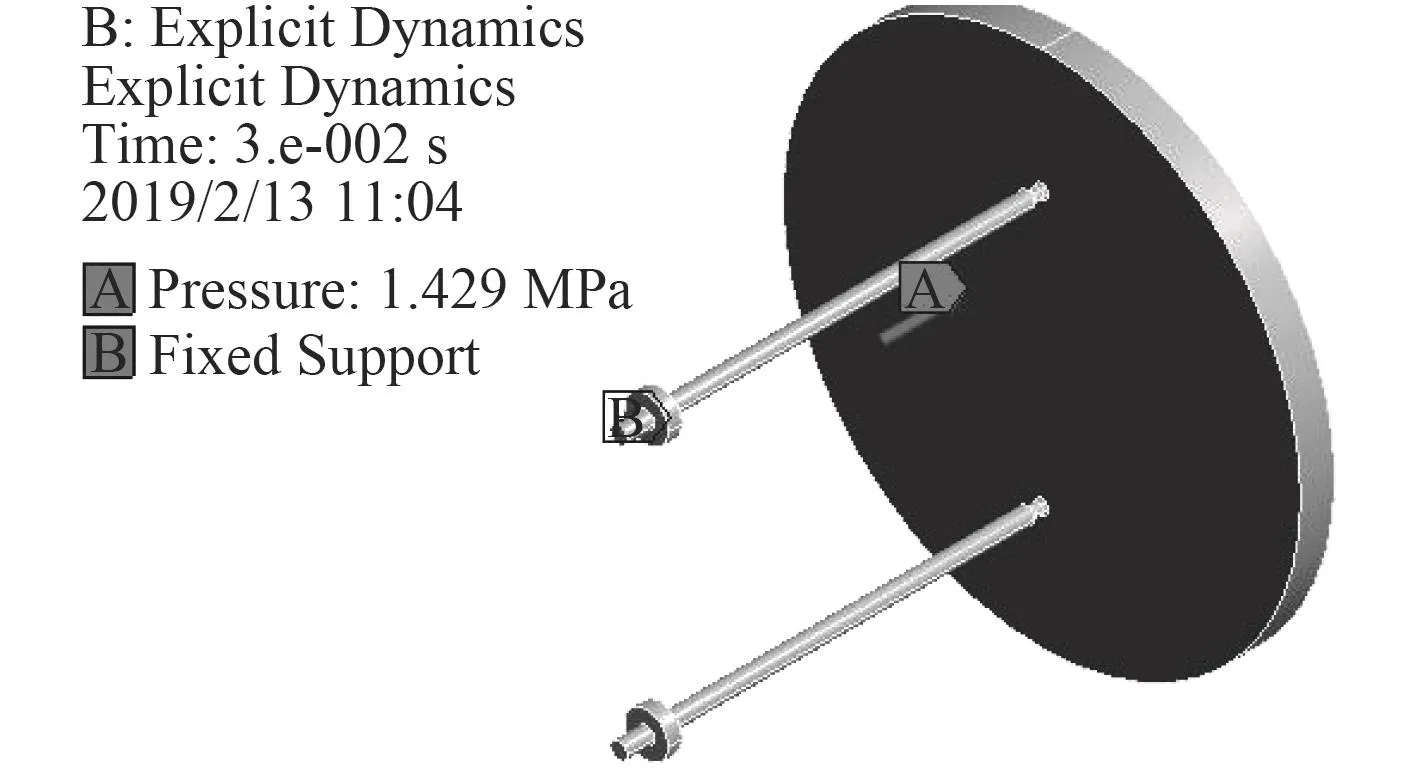
图4 拉断螺栓式固弹装置的边界条件Fig. 4 Boundary conditions of snap-bolt fixed device

拟合结果与压力试验曲线的对比如图5所示。

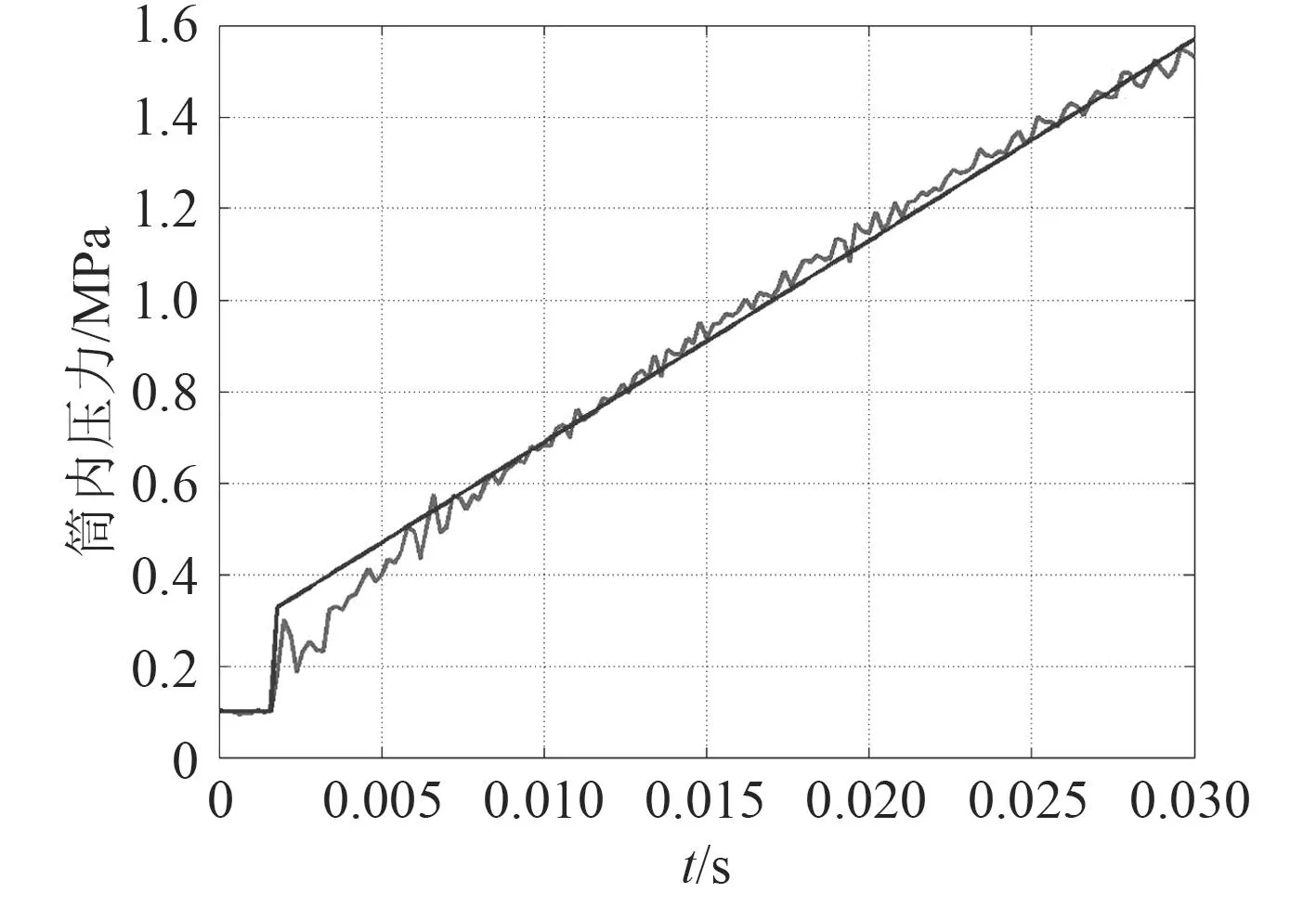
图5 压力边界条件及拟合曲线Fig. 5 Pressure boundary condition and fitting curve

仿真结果如图6及图7所示。结果表明，整个过程中拉断螺栓的最大Von-Mises等效应力为920.2 MPa，出现于0.018 s，约为拉断力设计值626.7 MPa的1.47倍。根据最大Von-Mises等效应力以及云图可确定拉断螺栓的拉断时间约为0.018 s。

3 发射内弹道模型及计算结果

通过对燃气蒸汽式发射內弹道计算模型[5 – 6]进行适当简化，并根据设计情况加入2×31500 N的拉断力后，初步建立了考虑拉断力的导弹发射内弹道计算模型。

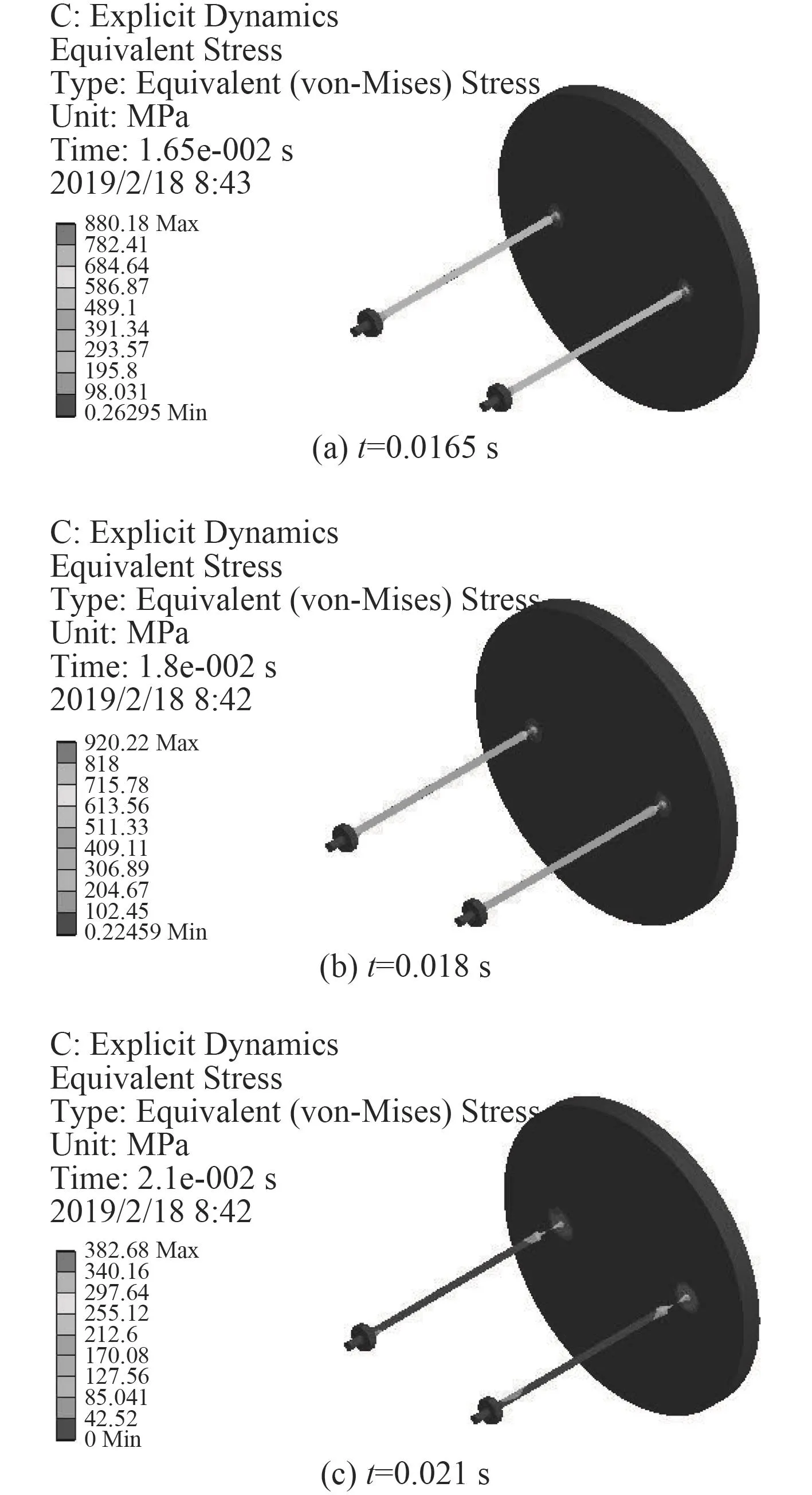
图6 拉断螺栓式固弹装置的Von-Mises等效应力云图Fig. 6 Von-Mises equivalent stress results of snap-bolt fixed device

通过与试验结果进行对比，该模型的计算精度较差，导弹的出筒速度、最大加速度、弹动时刻等发射内弹道特征值的计算/实测偏差较大，发射过程曲线的一致性不好。具体的特征值及曲线对比如表3及图8所示。

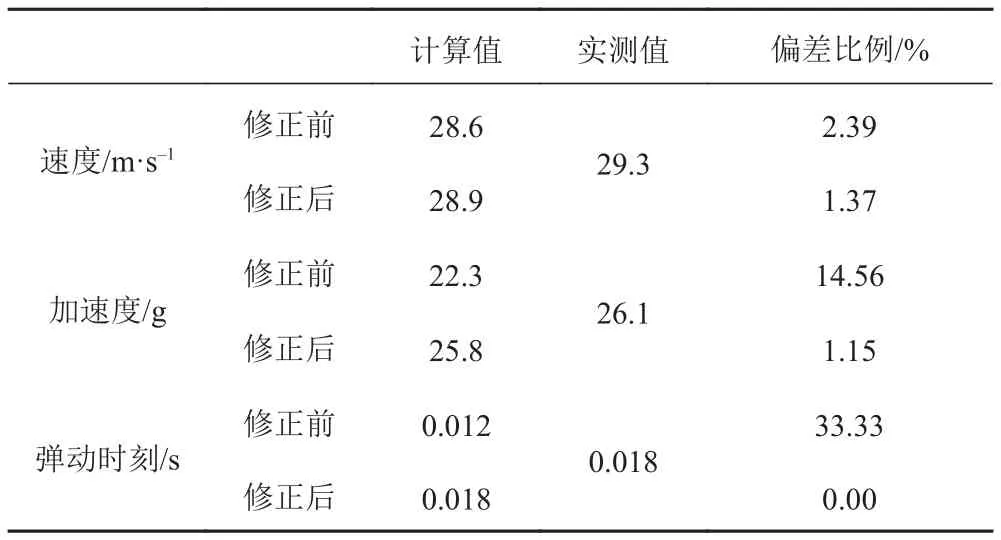
表3 发射内弹道特征值预示/实测对比Tab. 3 Comparison table of interior ballistics parameters between calculate and test results

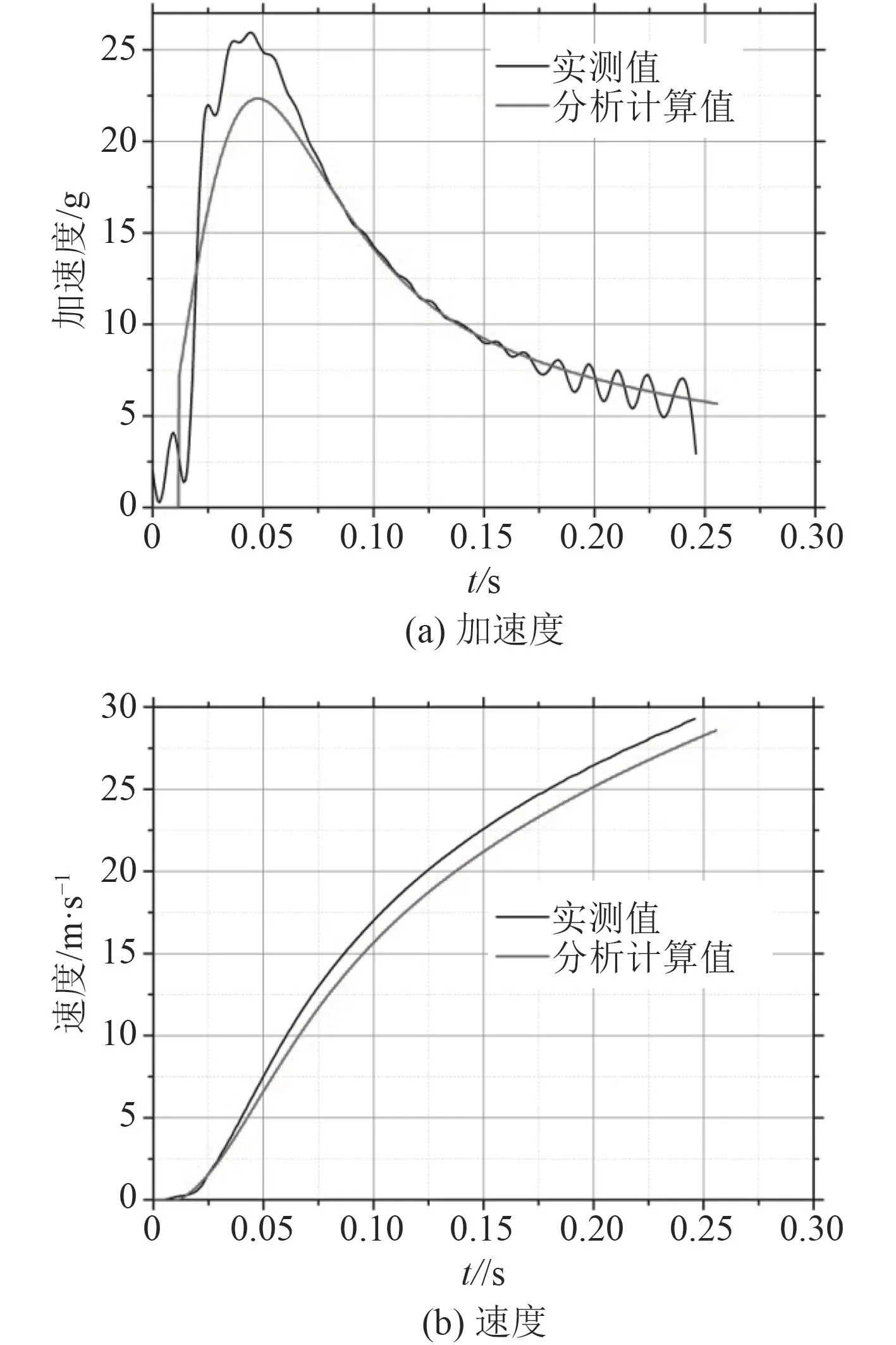
图8 发射内弹道过程曲线计算/实测对比Fig. 8 Curve contrast between original calculate and test results

经分析，导致此种现象的原因为：导弹发射过程中拉断螺栓式固弹装置实际的拉断力异于拉断力抽检试验的测试结果，因此根据仿真结果，将导弹发射内弹道模型中的拉断力由2×31 500N修正为1.47×（2×31 500N）。根据修正后的发射内弹道模型重新进行计算，曲线的一致性大幅改善，导弹的出筒速度、最大加速度以及弹动时刻等特征值的计算/实测偏差显著降低至≤1.5%。具体的特征值及曲线对比如表3及图9所示。

4 结 语

导弹发射过程中，由于应力加载速率（或应变率）差异，导致拉断螺栓式固弹装置呈现出异于静态或准静态下的动态力学性能。根据仿真结果，导弹发射过程中拉断螺栓式固弹装置实际的断裂应力约为准静态下的1.47倍。用该数据对发射内弹道模型中的拉断力进行修正，修正后的计算曲线与实测曲线吻合度较好，出筒速度、最大加速度以及弹动时刻的特征值计算/实测偏差≤1.5%。发射内弹道模型的计算精度显著提高，对导弹发射过程的精确控制具有重要意义。同时该方法对于其他类似问题的分析与解决具有一定借鉴意义。