邮轮推进器舱与吊舱推进器耦合振动分析

赵鹏飞，夏利娟，张 鑫

(1. 上海交通大学 海洋工程国家重点实验室，上海 200240；2. 高新船舶与深海开发装备协同创新中心，上海 200240)

0 引 言

豪华邮轮是我国从造船大国向造船强国发展转变亟待突破的领域，我国已将豪华邮轮建造技术作为“中国制造2025”主要目标之一。在邮轮振动研究领域，孙家鹏[1]从安全性、环保特性和规范3个角度分析了豪华邮轮的规范现状与发展趋势，并指出目前噪声已作为安全指标通过MSC.337(9)决议成为邮轮强制性要求。李兰美[2]指出舾装设备是产生振动噪声的主要来源，提高设备安装精度将显著降低振动噪声水平。在船体尾部振动研究领域，Biot M[3]对比分析了ISO 6954:1984与ISO 6954:2000两种振动标准在船舶建造与船东应用中的差异，并提出建立更为完善的ISO振动技术标准的建议。黄海燕、殷玉梅等[4 – 5]通过CFD方法求解螺旋桨脉动压力，并应用流固耦合等方法进行振动评估。

邮轮对操纵性和振动噪声有极其严格的要求，其动力装置主要采用吊舱推进器，本文研究对象为1艘采用双吊舱推进器的中型邮轮，位于推进器舱下的推进器螺旋桨脉动水压力将诱导产生船体振动，尤其以推进器舱区域最为严重。本文首先建立多个尺度范围的有限元模型，每种尺度包括用质量点模拟吊舱推进器的A类和完全建立吊舱推进器有限元模型的B类。在计算结构固有频率基础上分析吊舱推进器与船体耦合振动，确定计算模型最佳尺寸范围，并完成推进器舱结构振动响应计算分析。

1 湿模态振动计算

附连水质量对船体振动有较大的影响，常用的模拟附连水质量的方法有流体有限元法、Lewis图谱法、边界元法和经验公式法[6]。虚拟质量法基于边界元法，可在Patran或HyperMesh软件中设置船体外板湿表面，并通过语句定义附加质量矩阵，直接模拟船体与附连水之间的相互作用，本文即采用虚拟质量法进行振动频率与响应的求解。

通过在振动固有模态计算方程中考虑附加质量矩阵，实现了不可压缩理想流体对结构的作用。在静态不可压缩理想流体中不考虑阻尼效应的结构振动模态计算方程为：

式中： M 为结构质量矩阵； MA为附连水质量矩阵；加速度向量； u 为位移向量； K为结构刚度矩阵；KA为流体刚度矩阵。

流体刚度矩阵相对于结构刚度矩阵很小，可以忽略不计。且振动频率计算时阻尼对频率影响较小。但是在振动响应计算时，应当考虑到附连水对结构阻尼的影响。结构周围存在附连水，且受到激励力的作用时，结构振动响应方程如下式：

2 耦合振动分析

结构耦合振动是指在多自由度振动体系中，1个自由度上的运动与其所引起的另1个自由度上的运动并存时的振动。主船体与吊舱推进器在振动过程中相互影响，因此对相同尺度范围的两类有限元模型进行计算对比，分析吊舱推进器耦合的影响。此外，对同一类有限元模型，对比不同尺度范围的计算结果。

2.1 计算模型

本文研究的是1艘采用双吊舱推进器的中型邮轮，船体总长267 m，从船底板到上层建筑共有14层甲板。由于推进器舱受到螺旋桨脉动压力的直接作用，因此研究关注的区域为吊舱推进器上方的区域，如图1所示。本文以巡航工况作为计算研究的工况。

图1 邮轮尾部推进器舱舱结构布置Fig. 1 The general arrangement of cruise′s propelling machinery room

按照计算模型尺度从大到小，建立4个模型，分别为全船有限元模型、FR54模型、FR34模型和FR10模型。对每种模型按照是否含有吊舱推进器有限元模型分为A，B两类，共8个有限元模型。在FR54，FR34与FR10处设有横向舱壁，因此对FR54模型、FR34模型和FR10模型在对应横舱壁处固支。在振动计算中，按照船体实际装载修正有限元模型的质量分布。A类模型的吊舱推进器以质量点模拟，并应用MPC施加到船体上，如图2所示。B类模型则用板单元建立完整的吊舱推进器有限元模型，如图3所示。

2.2 吊舱推进器耦合振动对比分析

图2 四种 A 类有限元模型Fig. 2 FEM models of type A

图3 四种 B 类有限元模型Fig. 3 FEM models of type B

对A，B两类有限元模型的振动频率进行对比分析，以得到吊舱推进器耦合振动影响。全船有限元模型湿模态计算结果表明，固有频率小于6 Hz的振动以总体振动为主，在6 Hz以后则是以上层建筑局部结构振动为主。如表1所示，含有吊舱推进器的全船有限元模型B计算频率低于全船有限元模型A，以全船有限元模型B计算频率为基准，最大频率差异为6.8%。尽管两者总体振动振型相近，但由于模型A不含推进器舱三维结构，仅以质量点模拟，故无法得到单独吊舱推进器的振动模态，且会缺失部分尾部振动。

表1 全船有限元模型湿模态固有频率计算结果对比Tab. 1 Frequency comparison of whole ship models

FR54模型湿模态计算结果对比如表2所示，固有频率小于4.3 Hz的振动以该尾部舱段结构的总体振动为主。在扭转2阶模态两者振动频率差异为10.3%，耦合效果较大。除此之外FR54-A模型与FR54-B模型两者的计算固有频率差异很小，耦合效果不明显。但是FR54-B模型由于包含吊舱推进器的三维结构，能够体现出6.10 Hz的单独吊舱推进器振动模态。

表2 FR54模型湿模态计算结果对比Tab. 2 Frequency comparison of FR54 models

FR34频率对比分析结果如表3所示。以FR34-B模型振动频率为基准，受吊舱推进器的影响，2个模型在水平1阶频率差异较大，为17.8%，水平振动的耦合效应很大。除此之外，FR34-A模型与FR34-B模型两者的计算固有频率差异在低阶很小，且含有吊舱推进器的FR34-B模型振动频率较低。

表3 FR34模型湿模态计算结果对比Tab. 3 Frequency comparison of FR34 models

FR10模型区域仅包含推进器舱和吊舱推进器区域，计算范围最小。在不包含吊舱推进器的FR10-A中，局部振动较少，总体振动可以持续识别到19.76 Hz，在包含吊舱推进器的FR10-B中，出现较多吊舱推进器的局部振动。频率对比结果如表4所示，FR10-A模型与FR10-B模型两者的计算固有频率差异十分明显，除尾端垂向振动频率差异为7.3%，其他的频率差异都在10%以上。说明在模型范围较小时，吊舱推进器对推进器舱结构的振动效果很明显。同时，在FR10-A模型中计算能够出现的水平1阶振动和垂向2阶振动，在FR10-B模型中却没有体现。

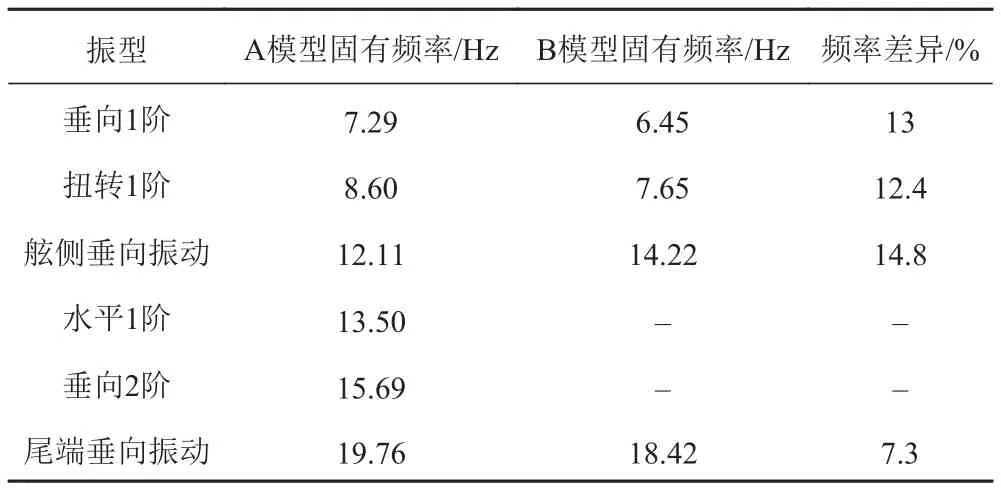
表4 FR10模型湿模态计算结果对比Tab. 4 Frequency comparison of FR10 models

综上4种模型的耦合振动分析可知，尽管吊舱推进器的质量只占全船质量的1.6%，但是对全船振动产生的影响不可忽略；在计算模型较大时耦合效果较小，但随着计算模型的缩小，耦合效果逐渐增大；在计算模型范围较大时，吊舱推进器对结构扭转振动耦合影响最大，如全船有限元模型和FR54模型的振动频率差异均在扭转振动时最大；在计算模型范围较小时，吊舱推进器对水平振动耦合影响最大。FR34模型水平振动频率最大差异为17.8%，且FR10-B模型未出现水平振动；含有吊舱推进器的B类模型计算结果能够显示吊舱推进器的局部振动。

因此，仅仅依靠质量点模拟吊舱推进器的计算结果与直接建立吊舱推进器的有限元模型振动频率差异明显，耦合振动影响不可忽略。

2.3 不同尺度模型振动对比分析

在结构响应计算中，有限元规模越小计算效率越高，但同时精度也更低。因此在耦合分析的基础上，对4个不同尺度的B类模型进行比较，以得到最适合振动响应计算的结构有限元模型。在振型对应的过程中，由于局部模型与全船有限元模型范围差异较大，因此以局部模型的总振型与全船结构有限元模型B的多节点振动对应。以FR54-B模型1阶垂向振动为例，FR54-B模型与全船模型B垂向振型对应如图4所示。

经过对振型的对应，FR54-B及FR34-B模型与全船模型B振动频率差异如表5和表6所示。可以看出，FR54-B模型的总体振动频率比全船模型B总体振动频率低。在第1阶垂向振动时，频率差异较大，为–13.8%。FR34-B模型1阶振动频率在全船模型B的3阶垂向振动与4阶垂向振动之间，与3阶和4阶垂向振动频率差异分别为11.7%和–18.6%，扭转和水平振动差异较小。FR10-B模型1阶垂向振动频率为6.45 Hz，而全船模型B计算得到的总体振动频率最大为5.80 Hz，高于5.80 Hz以上便是结构局部振动，因此无法将FR10-B模型与全船有限元模型B进行振型对比。

图4 FR54-B模型与全船有限元模型B垂向振型对应Fig. 4 The vertical mode vibration comparison between FR54-B and whole ship model B

表5 FR54-B与全船有限元模型B振动频率对比Tab. 5 Frequency comparison between FR54-B model and whole ship model

表6 FR34-B与全船有限元模型B振动频率对比Tab. 6 Frequency comparison between FR34-B model and whole ship model

通过上述分析可知，相比于其他局部模型以及全船模型，FR34-B模型尺寸范围适中，且计算结果较全船差异较小，兼具计算可靠性和经济性。

3 振动响应分析

螺旋桨激励是引起船体振动的主要激励源，船上90%的振动现象，是螺旋桨脉动压力引起的。脉动压力会引起局部结构共振和强迫振动，造成结构疲劳破坏，且降低居住舒适性。在计算中，对螺旋桨脉动压力进行分析，并应用OptiStruct与Nastran计算振动响应。

通过前面的振动对比分析可知，FR34-B模型的计算精度良好，模型尺寸范围适中，因此选用其作为振动响应计算的有限元模型。依据中国船级社规范施加脉动压力[7]，脉动压力施加在螺旋桨盘面之前0.1D，分布范围为D×D的正方形区域，D为螺旋桨直径。螺旋桨脉动压力在节点上的几何分布如图5（a）所示，同时脉动压力沿0～25 Hz以内的脉动压力频率曲线如图5（b）所示，在叶频与倍叶频处出现峰值，并在两侧呈三次方衰减。

图5 施加的螺旋桨脉动压力Fig. 5 Impulse excitation force

计算结果显示，推进器舱的垂向最大速度响应发生在叶频附近，如图6所示。最大垂向速度并没有发生在激励力正上方，而是位于2个吊舱推进器之间的船中区域。0～25 Hz 最大垂向速度响应为 6.42 mm/s，略高于BV船级社所规定6 mm/s的垂向速度响应。1～5 Hz最大垂向加速度响应低于规范要求的 188 mm/s2，因此对推进器舱结构仍有优化减振的空间。

图6 推进器舱垂向最大速度响应Fig. 6 The maximum vertical velocity response of propelling machinery room

4 结 语

推进器舱受到螺旋桨脉动激励力的作用，易产生结构振动并导致结构疲劳破坏。本文建立多个尺度的有限元模型，通过湿模态计算分析吊舱推进器与推进器舱的耦合振动效应，同时将局部模型振动模态与全船模型振动模态进行对比，选择出最佳尺度范围的有限元模型，并在此基础上完成振动响应计算，并与规范值对比，可为邮轮推进器舱结构振动优化工作提供参考。