含有随机参数的摩托车排气污染物工况法检测技术研究

叶帅宏 阮 立 陈 林 傅万进 葛凯杰

（台州市质量技术监督检测研究院 浙江 台州 318000）

引言

摩托车产业的发展以及产量的提高所带来的环境污染越来越受到人们的重视，为此国家相关部门以及研究机构着力于研究检测技术以期提高摩托车排气污染物检测的可靠性[1-5]。目前工况法测试是一种有效检测摩托车排气污染物的手段，但其受到环境温度、相对湿度等多种因素的影响，这些因素存在着很大的随机统计性，使得工况法检测结果存在一致性差的问题，如果采用多次试验的方法来解决存在的随机性问题势必会消耗大量的时间和费用。

一般认为常用的随机理论计算方法有Monte Carlo抽样法、正交响应面法等，下面利用随机理论计算方法建立工况法排气污染物质量随机分析模块，得到检测结果的区间值和统计信息，来全面了解试验情况。

1 排气污染物质量随机计算方程

根据标准[6]得到确定性的摩托车工况法排气污染物的质量MX（X分别为CO、HC和NOx，下同）计算方程为：

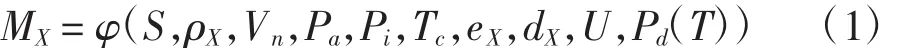
式中：S为行驶距离，ρX为排气污染物X的密度，Vn为定容泵排出气体的容积与转速的乘积，Pa为环境大气压力，Pi为大气压力与CVS入口压力差，Tc为定容泵进口截面处的稀释排气的平均温度，eX为收集在Sa袋内稀释样气中的X容积浓度，dX为收集在Sb袋内稀释样气中的X容积浓度，CCO2为取样袋中稀释排气的CO2浓度，CHC为取样袋中稀释排气的HC浓度，CCO为取样袋中稀释排气的CO浓度，U为相对湿度，Pd（T）为试验温度下水的饱和蒸汽压力（其值是由温度T引起的）。

而在实际情况下，通常认为由于设备测量及事物本身存在不确定性，使得所测得的环境温度T、相对湿度U等参数存在着随机统计性，这些随机性势必会引起检测结果即排气污染物质量的随机性，因此方程（1）可变为方程（2）：

2 排气污染物质量随机分析模块

2.1 Monte Carlo抽样方法分析模块

Monte Carlo抽样方法[7]是通过建立影响因素与结果之间的概率模型，对产生符合 某概率特征的随机数作为影响因素的值，进行多次确定性分析，通过求解得到概率统计信息来分析随机因素对结果的影响。由于Matlab程序中易于编写Monte Carlo程序中的不同区间下的均匀随机数发生器，随机抽样和计算结果的统计分析功能[8]，采用Matlab程序编制排气污染物质量Monte Carlo抽样方法分析模块，其程序流程如下：

1）对试验摩托车进行工况法排气污染物检测，得到行驶距离S、大气压力Pa等参数的测量结果值，并将其作为影响因素；

2）在matlab中读取影响因素的测量结果值；

3）定义Monte Carlo抽样次数n，用Matlab分别在随机变量xi区间[]上产生服从某一概率分布的随机数 r1，r2，…，rn；

4）运用计算方程（2），在Matlab中进行统计分析处理；

5）最后得到计算结果。

2.2 正交响应面法分析模块

正交试验方法[9]是一种有效研究典型因素对实验结果影响的随机方法，该方法以概率论和数理统计知识为理论基础，结合实践经验，通过建立正交试验表，进行多次因子试验，通过试验结果来分析归纳典型因素对实验结果的影响规律，为了缩短分析时间，在正交试验方法分析前先进行敏感度分析，去除敏感度低的因素。采用Matlab程序编制排气污染物质量正交响应面法分析模块，其程序流程如下：

1）对试验摩托车进行工况法排气污染物检测，得到行驶距离S、大气压力Pa等参数的测量结果值，并将其作为影响因素；

2）在matlab中读取影响因素的测量结果值，根据方程（2）和方程（3）[8]编写正交试验的灵敏度程序，并选取主要影响因素；

3）分别对排气污染物CO、HC和NOx设计正交试验表，选取的m个因素，各因素取n个水平，进行mn=q组正交设计试验，并在Matlab中计算处理；

4）编写Matlab程序语言，利用最小二乘法对试验的数据进行处理，构造响应面函数f（δ）[9]，并在Matlab中进行统计分析处理；

5）最后得到计算结果。

3 案例

在对某型号为HY125T-2A的摩托车进行排气污染物工况法检测时，得到行驶距离S、大气压力Pa等参数的测量结果值，并将其作为影响因素。然后在Matlab中读取影响因素的测量结果值，考虑设备测量及事物本身的不确定性，根据随机理论和工程处理方法，将上述不确定性参数在确定值的±2%之间视为均匀随机变量，影响因素的区间值如表1所示，利用正交响应面法分析模块分析得到各主要因素对试验结果的敏感性因子如表2所示。采用排气污染物质量随机分析模块得到计算结果值如表3和表4所示。

表1 排气污染物工况法随机影响因素

表2 各主要因素对试验结果的敏感性因子

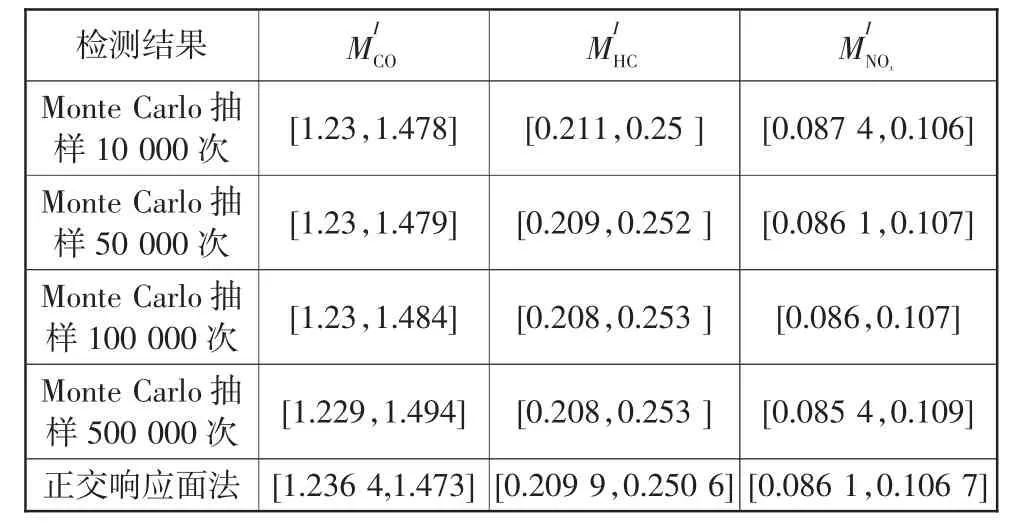
表3 随机分析模块计算排气污染物质量区间值g/km

表4 随机分析模块计算排气污染物质量的期望和方差g/km

从表2得到影响MCO的主要因素从大到小分别为 eCO、S、Pi、Vn、ρCO和 T，影响 MHC的主要因素从大到小分别为 eHC、S、Pi、Vn和 ρHC，影响 MNOx的主要因素从大到小分别为 eNOx、S、Pi、Vn、ρNOx、T 和 U。因此可以得到eX对MX影响最大，其次是S。其中T对MCO和MNOx有影响，U 和 Pa对 MNOx有影响。

以抽样次数500 000次的结果为参考解，计算得到Monte Carlo不同抽样次数和正交响应面法的左端点的误差（δL）和右端点的误差（δR）结果如表 5所示。

表5 随机分析模块计算排气污染物质量误差分析%

比较表5中随机分析模块计算排气污染物质量的左右端点误差值，可以看出随着抽样次数n的增加，排气污染物质量端点处的误差值越来越小，抽样100 000次时，其误差值越来越接近500 000次的值，因此可以得出Monte Carlo抽样精度与抽样次数n有关，并且随着抽样次数n的增加，抽样精度越来越高。正交响应面法计算所得的区间小于Monte Carlo方法计算所得的区间，但很接近Monte Carlo抽样方法。

4 结论

本文提出了应用随机理论计算方法建立工况法排气污染物质量随机分析模块，因此可以利用常用的随机理论计算方法如Monte Carlo抽样方法和正交响应面法。

该随机分析模块利用现有工况法测试程序，考虑检测设备及事物本身的不确定性，采用Matlab编写程序语言，实现对含有随机参数的摩托车排气污染物工况法的检测结果分析，得到计算结果统计值，拓展了摩托车排气污染物工况法检测时在考虑随机因素影响下的检测功能。

案例表明采用Monte Carlo抽样方法的抽样精度与抽样次数n有关，并且随着抽样次数n的增加，抽样精度越来越高，抽样100 000次时，其误差值越来越接近500 000次的值；正交响应面法计算所得的区间小于Monte Carlo方法计算所得的区间，但很接近Monte Carlo方法计算结果值；通过灵敏度分析，得到ex对排气污染物质量影响最大，其次是S。其中T对MCO和MNOx有影响，U和Pa对MNOx有影响。