基于正交实验的主反射镜轻量化设计

高天元，娄楠，韩旭，林鹤

（长春理工大学 光电工程学院，长春 130022）

空间激光通信发展迅速，相对传统空间通信方式，空间激光通信具有容量大、系统体积小、质量轻、功耗低、抗干扰能力强等特点［1-2］。在激光通信系统中，中继系统多由大口径反射式系统构成，本文使用卡塞格林系统作为中继系统。作为航空航天通信系统，在满足面型精度高，热稳定性好的基础上还需要满足重量轻，比刚度高的要求。为实现这一目标，需要对主反射镜进行轻量化设计。

目前针对主反射镜轻量化的设计大都基于经验设计或者拓扑优化法设计，这些方法都具有较大局限性，经验设计无法对轻量化主反射镜的性能进行量化，而拓扑优化设计虽然能对主反射镜结构参数进行优化，却不能同时考虑主反射镜结构尺寸的多个参数对主反射镜面型及重量的影响，无法对主反射镜结构进行全局优化。例如：杨佳文采用各参数灵敏性分析的方法对主镜进行优化［3］；于跃利用参数化迭代法设计法对反射镜结构进行优化［4］；包奇红在对一直径610mm的轻量化主镜进行设计时采用多岛遗传算法对各参数逐一进行优化［5］；谢杰采用有限元分析法，利用主反射镜的变形云图来分析各参数的对于主反射镜面型的影响［6］；王富国在对1.2mSIC主反射镜进行轻量化设计时采用的是有限元法与经验设计法相结合的方法［7］。

以一对多激光通信中继系统中的主反射镜作为研究对象，运用正交实验的方法对不同参数组合下的主反射镜进行光机热集成分析，通过有限元软件辅助分析来对主反射镜的各个参数进行优化设计，通过多参数全局优化最终得到综合性能最优的主反射镜结构。

1 主反射镜结构与正交实验方案

1.1 主反射镜结构

主反射镜来源于空间用一对多激光通信中继系统的主反射镜。主反射镜为口径为276mm，球半径为675mm的抛物面镜，工作波段为近红外波段。由于为中小口径空间用反射镜，因此镜体材料拟采用SIC-CVD，SIC-CVD有比刚度高，导热性能出众，热稳态变形小等特点。

由于主反射镜的径厚比会对主反射镜的应变产生影响，因此引入平板实心镜体的径厚比Δ计算经验公式［4］，对主反射镜尺寸进行估算：

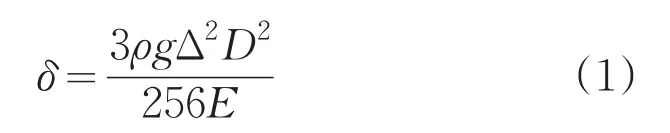
式中，δ为镜面允许最大变形量（按照λ=632.8nm的PV值等于10），单位为μm；g为重力加速度；ρ为材料密度，单位为kg/m3；D为主反射镜的直径，单位为m；E为材料的弹性模量，单位为Mpa。由此可以计算出Δ=10.12，并推算出主反射镜的厚度约为25mm，因此在建模过程中将主反射镜设计为中心厚度25mm。

主反射镜的支撑拟采用背部支撑的方式，支撑点个数也会对镜面的面型产生一定的影响，在此引入公式［4］对其进行计算：

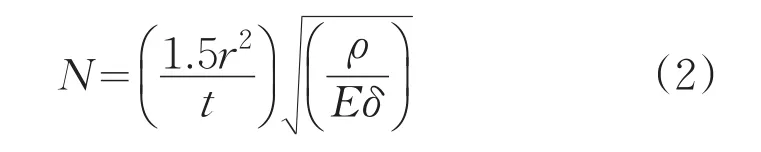
式中，N为支撑点个数；r为主反射镜的半径，单位为m；t为主反射镜的厚度。由此可算出N=3.2，因此背部支撑点个数按照3个来设计。

此外，主反射镜的轻量化形式拟采用背部开放式三角形孔的形式对其进行减重，主反射镜模型的参数化建立由SolidWorks软件完成，如图1所示。

图1 主反射镜结构示意图

1.2 正交实验方案

主反射镜的工作环境温度为15℃～25℃，标准工作温度为20℃，此外，由于在地面进行装调与检测，因此需要考虑1G重力释放的工况。此物理场作用下有众多因素制约着主反射镜面型的变化大小和主反射镜的整体重量大小，为了弄清哪些因素最为敏感，哪些因素搭配会产生极值，如何才能在众多组合中选出最优，在此引入正交实验的方法，来对主反射镜的结构进行优化。

根据主反射镜结构特点选取4因素3水平的正交表，4因素用a、b、c、d表示，其中a表示背面筋的厚度大小，单位为mm；b表示主反射镜轻量化孔的内切圆大小，单位为mm；c表示反射镜面的厚度大小，单位为mm；d表示主反射镜支撑孔的径向位置（支撑孔的径向位置用其圆的直径表示），单位为mm。正交表L9(34)，如表1所示。

表1 L9(34)正交实验方案表

2 主反射镜建模与支撑结构的建立

2.1 主反射镜建模

利用patran软件进行建模，由于正交实验需要对同一模型修改不同参数反复进行仿真，因此将主反射镜进行参数化建模，镜面与后表面的筋近似为2维单元以方便修改［8］，网格采用手动划分的形式［9］，网格划分的效果如图2所示。

图2 主反射镜有限元模型

2.2 约束的设立

约束的设立决定了支撑结构的形式以及仿真时边界条件的设立，最后将直接影响到设计优化的结果，因此约束的设立显得格外重要。在此引入运动学支撑的概念，所谓运动学支撑是指方案中被支撑刚体结构的所有刚体运动刚好被完全限制，此时被支撑结构与其他刚体构件之间不存在弹性耦合［11-12］。

对于三维空间中的主反射镜来说有六个自由度，分别为三个平动自由度和三个转动自由度，有多种方式可以来对主反射镜进行约束。主反射镜工作环境有温度的变化，此时由于主反射镜材料和主反射镜支撑底座材料的热膨胀系数不同，二者之间存在着径向连接位置的位移差，进而容易产生应力应变。为了最大限度减小温度变化引起的热应力，在此选择三槽构型对有限元模型进行约束，三槽构型属于运动学支撑的一种形式，如图3所示为三槽构型的优选方案，此时以旋转抛物面的原点为坐标原点建立柱坐标系。在设立约束时，限制其周向位移与轴向位移两个自由度，释放径向位移的自由度，此时的有限元模型在温度变化的条件下不会发生偏心：

图3 三槽构型约束示意图

以光轴同抛物面的交点为圆心建立圆柱坐标，对于三个支撑点约束其周向转动和轴向的平动，释放其径向平动自由度，这样一来在工作环境温度的变化下，允许镜体的径向膨胀收缩，限制了其周向转动以及沿光轴方向位移，在保证镜体偏心和沿轴位移量最小的情况下最大限度地减小了镜体所受的应力。如图4所示为主反射镜变形云图：

图4 25℃，1G重力释放条件下主反射镜变形云图（mm）

2.3 支撑结构

尽管理想化的运动支撑在实际中不可能实现，支撑结构仍然需要向理想运动模型上靠拢。若采用两脚架的形式对主反射镜进行支撑，接触部分采用挠性元件进行连接［10］，此时的约束条件和理想条件下的三槽构型最为接近，结构如图5所示。

图5 主反射镜两脚架支撑结构示意图

3 仿真实验结果与讨论

根据表1的表格中各个因素和取值，通过patran和nastran模拟仿真，计算出9种方案下的模型节点刚体位移。将节点初始坐标与节点位移量导出，通过矢高位移法计算出工作环境下镜面的RMS值，对比不同的方案下主反射镜面型RMS值和轻量化程度来选取最优的方案。定义主反射镜轻量化比［11］为主反射镜轻量化结构减去的质量占未轻量化结构的质量的比值，对于主反射镜轻量化程度分析则可根据表格2中的各因素和取值，通过SolidWorks软件对比无轻量化结构主反射镜和轻量化之后主反射镜的质量，以此来对比不同方案下主反射镜的轻量化。

Ki为任一列上水平号为i时，对应的结果之和，ki：ki=KiS，其中S为任一列上各水平出现的次数；Rk（极差）：在任一列上：

Rk=max{k1,k2,k3}-min{k1,k2,k3}。

Qi为任一列上水平号为i时，对应的结果之和，qi：qi=Qi/S，其中S为任一列上各水平出现的次数；Rq（极差）：在任一列上：

Rq=max{q1,q2,q3}-min{q1,q2,q3}。

表2 25℃，1G重力释放条件下不同组合下主反射镜RMS值和轻量化比

表3 25℃，1G重力释放条件下各参数RMS值水平

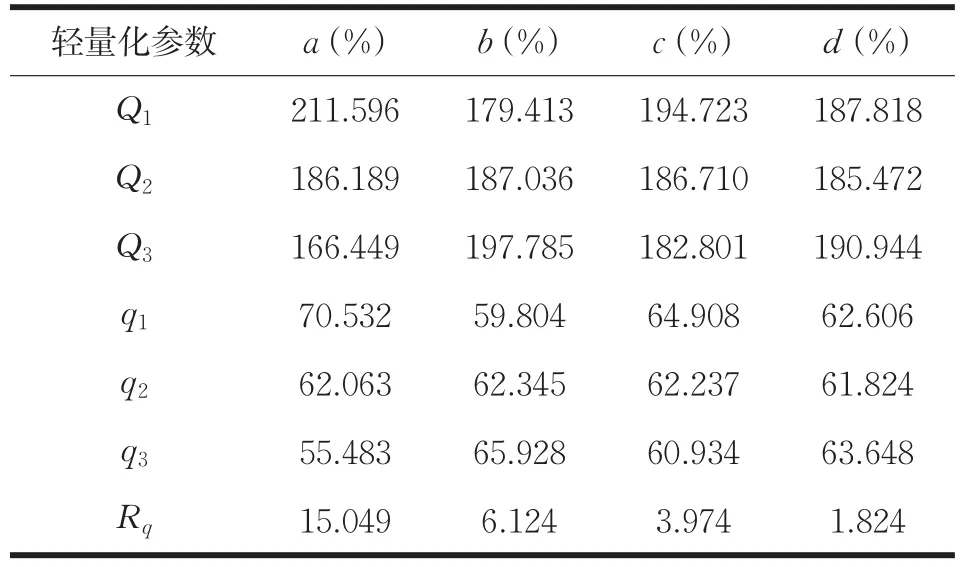
表4 25℃，1G重力释放条件下各参数轻量化比水平

由于多个因素之间相互影响，因此需要将多因素结合对比，比较图6（a）中的运算结果中每一个因素各水平条件的均值，可以得出最优组合为a2b2c1d2，即主反射镜背面筋厚度为3mm；轻量化孔内切圆大小为33mm；反射面厚度为2mm；支撑点径向位置圆大小为176mm。通过该参数返回实验进行建模仿真运算，可以得出RMS值为2.961nm。此时镜体质量为1.855kg，轻量化比为69.038%

表3的极差分析数据表明，各因素对于主反射镜面型变化的影响敏感程度的关系大概为d＞c＞a＞b，即主反射镜支撑孔的径向位置对主反射镜面型的影响最大，随后是主反射镜反射面厚度，再次是主反射镜背面筋厚度，对主反射镜面型影响程度最小的为轻量化孔内切圆大小。由图6（a）参数变化趋势可以看出在取值范围内，因素a主反射镜背面筋厚度在3mm时，主反射镜面型RMS值最小；因素b主反射镜轻量化孔内切圆大小在为36mm时，主反射镜面型RMS值最小；因素c反射面厚度在2mm时，主反射镜面型RMS值最小；因素d主反射镜背面支撑点径向位置圆大小在198mm时，主反射镜面型RMS值最小。

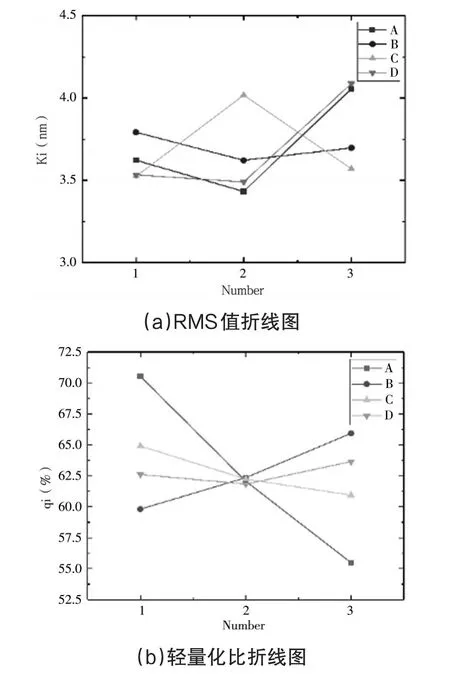
图6 各参数影响敏感程度对比折线图

由于主反射镜为空间激光通信基台中继系统的一部分，所以在设计之初在考虑其光学性能的同时应兼顾其重量，因此其轻量化比也是设计优化的一个重要参考因素。参考表4，可以得出关于轻量化比的最优组合为a1b3c1d3，即主反射镜背面筋厚度为2mm；轻量化孔内切圆大小为36mm；反射面厚度为2mm；支撑点径向位置圆大小为198mm，此时主反射镜的轻量化比为77.57804%，主反射镜重量为1.3435kg，减重量达到4.6484kg。各因素对于主反射镜轻量化比影响大小程度的关系应为a＞b＞c＞d，即主反射镜背面筋厚度对主反射镜重量影响最大，主反射镜支撑点径向位置圆大小对其影响最小。

由图6（b）参数变化趋势可以看出在取值范围内，因素a主反射镜背面筋厚度越小，主反射镜轻量化比最大；因素b主反射镜轻量化孔内切圆大小越大，主反射镜轻量化比越大；因素c反射面厚度越小时，主反射镜轻量化比越大；因素d主反射镜背面支撑点径向位置圆大小在198mm时，主反射镜轻量化比最大。因素d对于主反射镜的轻量化的影响可以忽略不计，因此主要考虑a、b、c三个因素。

通过图6（b）比较可知，因素a（主反射镜背面筋厚度）对于主反射镜轻量化比影响极大，通过减小主反射镜背面筋的厚度可以极大得减小主反射镜的重量，所以在此可以选择折中方案a1b2c1d2，可以保证主反射镜的面型偏差在较小的范围内的同时达到相对较大的轻量化比。模拟仿真结果表明，该折中方案中主反射镜面型的RMS值为2.976nm，相对于RMS值最小的组合面型精度差极其微小，但其轻量化比为75.029%，轻量化后质量为1.496kg，相比RMS值最小组合的轻量化比增加了5.991%，而这些减轻的重量对于航空航天来说拥有极其重要的意义。

4 结论

基于正交实验法和有限元分析软件可以成功实现主反射镜在多物理场下多结构参数的优化设计。研究结果表明工作环境下，对于主反射镜面型精度影响最敏感的因素为主反射镜背面支撑孔位置，而影响主反射镜轻量化比的主要因素为主反射镜背面筋厚度。将主反射镜面型精度最高组合同轻量化比最高组合进行折中设计，所得的主反射镜结构为主反射镜背面筋厚度为2mm；主反射镜轻量化孔内切圆大小为33mm；反射面厚度为2mm；主反射镜支撑点径向位置圆大小为176mm。本文阐述了一种基于正交实验的主反射镜结构优化方法，相较传统的拓扑优化法具有多因素同时优化，实验过程简单的优点。