基于多元回归的原液着色纤维混色规律研究

买 巍 丁彩玲 马崇启 张健飞 辛 欣

(1.山东如意科技集团有限公司，山东济宁，272073；2.天津工业大学，天津，300387；3.天津纺织工程研究院有限公司，天津，300193)

传统的纺织生产，其印染过程用水量大，同时会产生大量的废水。原液着色是一种“绿色纤维”生产技术，原液着色纤维在生产过程中就被赋予了各种颜色，因此下游生产的过程中就省去了印染环节，具有突出的环境友好特征[1]。但原液着色纤维混色属于固相混色，其混色机理十分复杂。目前使用原液着色纤维的大多数企业主要还是根据来样颜色，由配色人员依据经验将不同比例异色纤维纺成细纱或者织成织物与来样进行比对，其耗时长、误差大。

近年来，利用光谱技术与多元校正分析相结合在计算机配色领域有众多的研究成果。如利用反射光谱数据对计算机配色的质量进行评估研究[2]，基于原色纤维混配色织物的呈色特性与影响因素的研究[3]，对原液着色纱线采用SN模型的全光谱配色算法研究[4]，采用Friele模型的色纺纱光谱配色研究[5],基于共轭梯度法的纱线染色配方预测优化算法研究[6],用于染色的神经网络计算机配色算法研究[7]等。但由于纤维混色机理复杂，多数配色模型均存在一定的误差，难以应用于企业。在文献[8]、文献[9]中均提到可以利用可见光吸收光谱实现混合染料的颜色预测。而利用可见反射光谱对混色纤维进行颜色预测研究并不多见。如果能通过计算机实现混色纤维的颜色预测，结合人工进一步进行配色修色，不仅能缩短配色时间，同时还能提高一次配色成功率，从而缩短配色周期，提高产品生产效率。

1 试验部分

1.1 样品

样品采用大红色、旦黄色、宝石蓝色三种涤纶原液着色纤维，均为滁州安兴环保彩纤有限公司提供，纤维长度38 mm，线密度1.56 dtex。不同颜色的纤维按照一定的比例进行三色混和，得到60个样本。随机选择40个样本用于训练集，混和比例如表1所示，剩余20个用于预测。

表1训练集混色纤维质量比

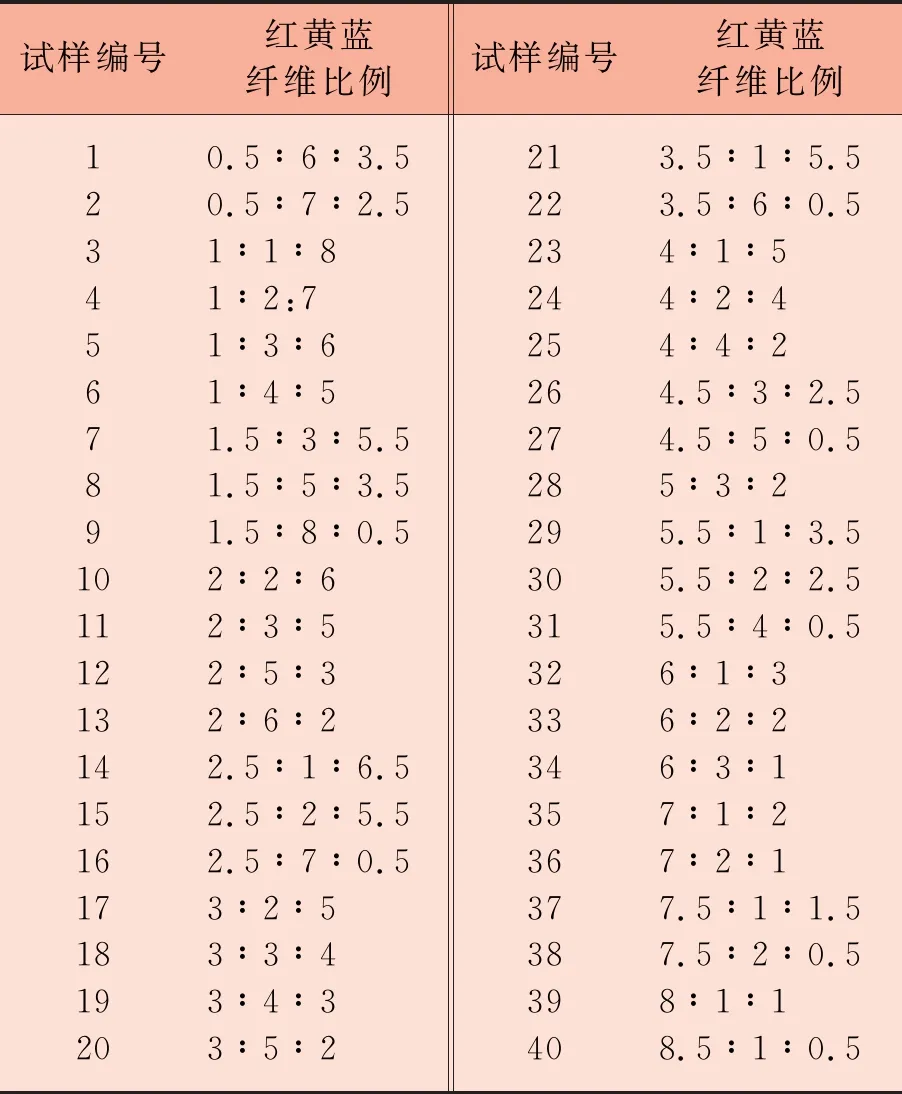
试样编号红黄蓝纤维比例试样编号红黄蓝纤维比例12345678910111213141516171819200.5∶6∶3.50.5∶7∶2.51∶1∶81∶2:71∶3∶61∶4∶51.5∶3∶5.51.5∶5∶3.51.5∶8∶0.52∶2∶62∶3∶52∶5∶32∶6∶22.5∶1∶6.52.5∶2∶5.52.5∶7∶0.53∶2∶53∶3∶43∶4∶33∶5∶221222324252627282930313233343536373839403.5∶1∶5.53.5∶6∶0.54∶1∶54∶2∶44∶4∶24.5∶3∶2.54.5∶5∶0.55∶3∶25.5∶1∶3.55.5∶2∶2.55.5∶4∶0.56∶1∶36∶2∶26∶3∶17∶1∶27∶2∶17.5∶1∶1.57.5∶2∶0.58∶1∶18.5∶1∶0.5

1.2 设备及制样测试方法

试验仪器：天津市嘉诚机电设备公司生产的小型数字式梳棉机、小型数字式并条机、小型数字式粗纱机和小型数字式细纱机；常州第二纺织机械厂生产的Y381A型摇黑板机。

制样及测试方法：总质量为25 g的混和纤维，经过事先混和，通过梳理、并条、粗纱、细纱等工序，纺成18.44 tex，捻系数360的细纱，通过摇黑板机制成纱线色卡。采用Datacolor SF600 Plus型分光光度仪测试纱线的光谱数据。测试条件：D65标准光源，30 mm孔径。每个样品在不同位置测量10次，取平均值，得到400 nm～700 nm时样品的可见反射率光谱和色度学参数。

2 评价方法

对于配色效果的评价，最重要的评价指标应为色差，即两个样品在色觉上的差异。人眼对于颜色的感知主要由样品色度学参数明度L*、彩度C*和色相H*决定。因此色差也是明度差(DL*)、彩度差(DC*)以及色相差(DH*)的综合评价。若颜色空间均匀分布，那么可以直接用色度坐标对应的欧式距离来反应色差的大小。但多数情况下，色彩空间中两种颜色的几何距离不一定可以表示两种颜色在色觉上的差异，若依照颜色立体状态下的几何空间划分，并不符合人眼的色觉。因此需要建立色差公式对不同样品的颜色差异进行评价。对于纺织品采用较多的是CMC(2∶1)色差公式[10]。公式如下所示。

(1)

式中：DL*表示明度差,DC*表示彩度差，DH*表示色相差；SL、SC、SH分别为修正系数；l和c分别为调整明度和彩度的相对宽容系数。

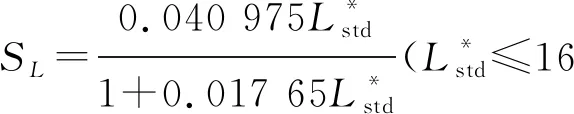
(2)

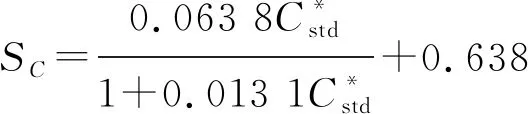
(3)

SH=SC(tf+1-f)

(4)

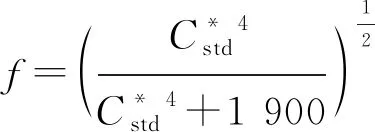
(5)

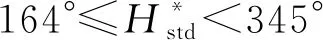
3 结果与讨论

3.1 样本可见反射光谱

图1为训练集样本可见光谱反射率曲线。

图1 训练集反射光谱图

样本明度L*、彩度C*和色相H*等色度学属性均能在光谱反射率曲线中得到体现。反射率曲线的高低表示L*值的大小，L*值越大，反射率曲线越高；曲线反射峰的宽窄,表示C*的高低，反射峰越窄，C*值越高；曲线峰值反射率对应的波长表示该颜色的色相H*。从训练集光谱图可知，样本波峰从450 nm～700 nm，覆盖了主要颜色波段，说明训练集研究选择的混合比例合理。色度学参数统计结果如表2所示。

表2训练集样本统计结果

数据集样本数L*平均值 标准偏差C*平均值 标准偏差H*平均值 标准偏差训练集 预测集 总数据集40206037.5530.5435.226.5315.569.5718.8224.4520.7010.2215.3511.45124.21136.98128.4340.1948.2632.35

3.2 预测模型建立

设旦黄色纤维配比为x1，宝石蓝色纤维配比为x2，大红色纤维配比为x3，根据表1可知，x1+x2+x3=10。由于试验所用三种颜色的纤维总含量不变，所以已知旦黄色、宝石蓝色两种纤维含量时，大红色纤维含量也可得到，即回归模型只需两种纤维比例含量作为自变量。

3.2.1 两种纤维其中一种纤维含量固定时的模型

固定宝石蓝色纤维含量，则L*、C*、H*与旦黄色纤维含量模型归纳为L*=f(x1)，C*=f(x1)，H*=f(x1)。利用SPSS软件进行一元回归分析，可得到L*、C*、H*与x1的回归方程，如x2=0.1时，L*=24.069x1+31.314，C*=38.173x12-41.921x1+43.034，H*=82.315x1+9.191 8。具体结果见表3和图2。

表3方程相关系数和方程显著性分析

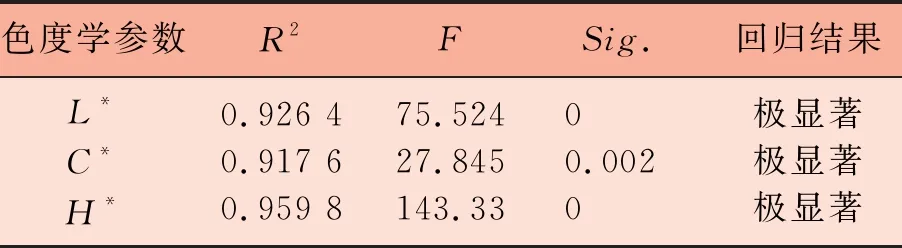
色度学参数R2FSig.回归结果L*C*H*0.926 40.917 60.959 875.52427.845143.3300.0020极显著极显著极显著

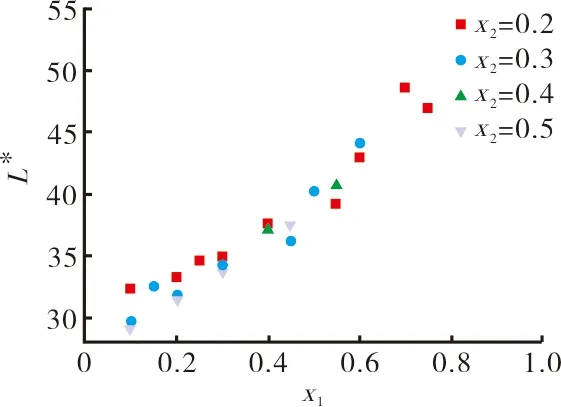
(a)L*与纤维比例关系(c)H*与纤维比例关系

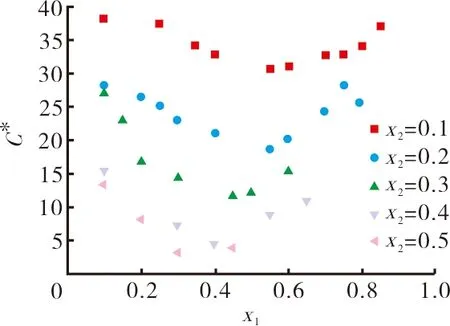
(b)C*与纤维比例关系

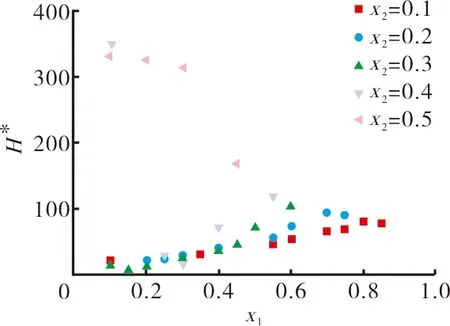
(c)H*与纤维比例关系

图2 固定一种纤维含量时L*、C*、H*随纤维比例变化关系

根据表3和图2结果，L*与x1呈线性关系；C*与x1采用二元多项式拟合可得到较好回归效果；H*与x1，当x2≤0.3时，采用线性拟合效果较好，x2>0.3时无明显规律。

3.2.2 两种纤维含量均改变时的模型

两种纤维含量均改变时，L*、C*、H*与旦黄色纤维含量模型归纳可为L*=f(x1,x2)，C*=f(x1,x2)，H*=f(x1,x2)。对L*、C*、H*分别利用SPSS进行多元回归分析。

对于L*=f(x1,x2)回归模型，采用多元线性拟合得到L*=30.303+24.78x1-5.323x2。R2=0.928，回归系数t检验x1=15.883，Sig.=0，x2=-3.413，Sig.= 0.002。由L*值与纤维比例拟合的相关系数及显著性检验可知，回归系数t检验结果均为极显著，同时该方程经过F检验，F=212.209(Sig.=0)，说明多元线性回归达到预期效果。

对于C*=f(x1,x2)回归模型，采用二元多项式拟合得到C*=55.042x12+134.133x22-55.293x1-148.592x2+58.404。R2=0.983，回归系数t检验x1=-10.815，Sig.=0，x2=-29.064，Sig.=0，x12=8.715，Sig.=0，x22=21.239，Sig.=0。由C*值与纤维比例拟合的相关系数及显著性检验可知，该方程F显著性检验为F=457.602(Sig.=0)说明F远大于临界值，同时通过t检验，各系数t值也大于临界值，显著性极显著。因此可以采用二元多项式进行拟合。

对于H*=f(x1,x2)回归模型，采用多元线性拟合得到H*=-12.634+119.977x1+55.478x2。R2=0.891，回归系数t检验x1=9.757，Sig.=0，x2=1.758，Sig.=0.006。由H*值与纤维比例拟合的相关系数及显著性检验可知，当x2>0.3时规律不明显。因此选择x2≤0.3数据建立模型，回归方程相关系数0.891，但整体方程F显著性检验F=47.613(Sig.=0)，且回归系数t检验也很显著，因此x2≤0.3时使用多元线性拟合也能得到较好的效果。

3.3 模型预测及精度分析

从预测集样本中选择x2≤0.3的样本共14个，采用研究的模型预测L*、C*、H*，预测数据与实际测试数据比较结果如图3所示。

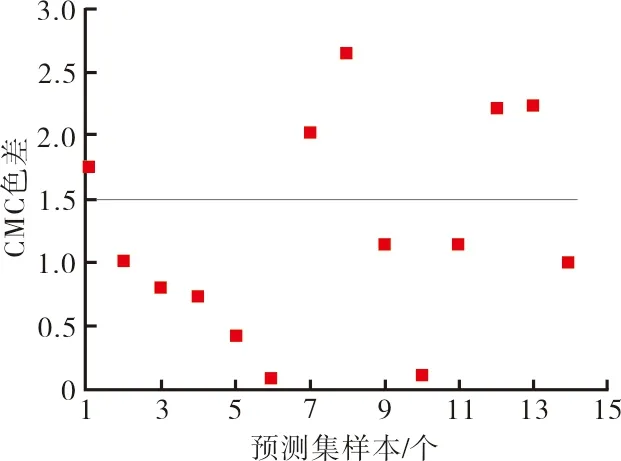
图3 预测集样本色差

CMC色差小于1.5的样本占总预测样本的64%，最大CMC色差也小于3。通常实际CMC色差要求小于1.5即可。综合考虑模型及测试中的误差，根据研究得到的模型对于混色纤维颜色预测，其精度能够满足要求。

4 结论

本文利用SPSS软件，将单色纤维比例含量和多色纤维比例含量分别进行回归分析，导出混色纤维比例含量与L*、C*、H*值之间的数学模型。试验证明，通过该模型可以初步预测不同颜色纤维混色后的颜色，且与实际数据之间的色差较小，能够提高人工配色的一次成功率，从而缩短配色的时间。限于研究的局限，色相H*与纤维含量的规律还不十分明确，有必要做更深一步研究。同时在实际的配色过程中，单色纤维种类往往更多，数据量更大，采用多元回归分析方法得到的色差还有必要进一步分析。