基于结构可靠度的建筑全生命周期成本分析

黄建瓯,罗 方

(1.莆田学院 土木工程学院,福建 莆田 351100；2.中国航天科技集团 航天材料及工艺研究所，北京 100000)

钢筋混凝土结构(reinforced concrete，RC)(简称RC结构)建筑在我国建筑总量中占据很大的比例，其钢筋的锈蚀和混凝土的耐久性问题将给建筑带来严重危害。国家统计数据显示，我国大多数已建钢筋混凝土建筑的结构可靠度存在严重的问题，建筑结构主体的腐蚀使得年损失达到约1 000亿元[1]。英美等国家已在建筑结构可靠度上吃了大亏，美国某科研机构通过调研发现,全美国172家医疗机构约2 000栋建筑的结构可靠度不足，造成的养护费用约为建设费用的7.7倍。另据美国运输部门1989年提交给国会的一份报告显示，美国当时积压待修的混凝土桥梁的维修费用高达1 550亿美元，是当初建造费用的4倍。鉴于此，美国学者提出了全生命周期成本分析(life cycle cost analysis,LCCA)法，该方法在英美等国家得到了广泛应用，并纳入政府法令，作为政府评估工程、计算工程成本及实行招投标的依据。我国目前正处于工程建设的高峰期，如果不及时从全生命周期的角度重视工程结构可靠度问题，建筑结构中病害的严重发生将使得国家不堪维修和重建的经济负担，进而影响国家经济发展。国内学者关于工程结构可靠度的分析大多从结构性能和力学角度进行分析，关于LCCA的研究成果亦多以全生命周期成本的理论及其在各领域的应用为主，较少从结构可靠度的角度进行全生命周期经济分析。笔者力图将工程结构可靠度分析与LCCA相结合，从结构可靠性设计角度考虑建筑全生命周期的经济性，研究工程结构可靠度与全生命周期成本之间的函数关系，构建基于结构可靠度的RC建筑全生命周期成本分析流程，并结合实际案例进行佐证。

1 建筑结构可靠度及LCCA综述

《建筑结构可靠性设计统一标准》(GB50068-2018)中对结构可靠度的定义为：“建筑结构在规定的时间内，在规定的条件下，完成预定功能的能力。”[2]其中，预定功能通常指在正常使用的前提条件下能够承受可能发生的各种作用，包括安全性、适用性和耐久性。规定的时间指的是工程结构的设计使用寿命，对于既有建筑指的是剩余使用寿命。金伟良等[3]提出应在混凝土结构设计中引入全生命周期成本的理念，研究基于结构全生命周期成本(life cycle cost，LCC)的混凝土结构耐久性设计基础理论，以及如何进行全生命周期的可持续设计，但仅限于理论提出。方永锋等[4]对传统结构可靠度算法进行改进，利用改进的遗传算法生成响应面函数，并利用一次二阶矩法对结构可靠度进行计算。刘俊卿等[5]则从模糊数学的角度对沥青路面的结构可靠度进行分析。综合分析国内理论成果，可发现对RC结构可靠度的研究偏重于单纯可靠度的计算，缺乏从全生命周期经济性角度进行可靠度分析。

全生命周期成本分析概念最早由美国学者于二十世纪七八十年代提出，后得到英国皇家测量师学会的大力推广和应用，最具有代表性的是英国FLANAGAN[6]提出的一系列LCCA理论：“LCCA所涉及的问题”“全生命周期成本分析的理论和实践”“全生命周期成本分析在建筑工程中的应用”，英国皇家测量师学会更是组织一批专家学者先后出版了《全生命周期造价管理范例》《全生命周期成本核算与设计手册》《建筑全生命周期成本分析指南》等工具书和专著。政府层面上，美国政府出台了一系列LCCA执行法令，率先用于公路与交通工程的设计、项目投资评估和成本计算。我国电力部门及相关国家部委已委托东南大学科研机构在电力工程领域实行LCCA的应用研究，力求在电力工程领域率先实行全生命周期成本分析法。

2 基于结构可靠度的建筑LCC构成及计算模型

2.1 建筑LCC构成、影响参数及计算原理分析

钢筋混凝土结构的可靠度主要体现在耐久性、安全性和适用性3个方面，其中至为关键的是耐久性，如果耐久性没问题，理论上讲安全性和适用性也不会有问题。当结构的耐久性出现问题时会降低其安全性和适用性，当降低到一定程度时就需要人工干预强行进行维修以提高其安全性和适用性。建筑结构耐久性将直接决定建筑的使用寿命，由于全生命周期成本的计算需要将未来成本折现到计算时点进行计算，折现率和建筑的使用寿命将是成本计算的关键参数，在进行建筑LCCA时需提前确定建筑的耐久性以便于计算建筑使用寿命。

建筑工程全生命周期成本由初始建设成本、预防性维修成本、工程检测成本、工程维修加固成本及工程失效成本组成。ESTES等[7]给出了基于结构可靠度的建筑LCC计算式，如式(1)所示。

LCCE=CI+CPM+CINS+CREP+CFAIL

(1)

式中:LCCE为建筑全生命周期成本总期望值；CI为结构初始建设成本；CPM为预防性维修成本，即日常维修成本；CINS为工程检测成本；CREP为维修加固成本；CFAIL为工程失效成本。

在进行建筑全生命周期成本分析时，需将未来发生的运营维护成本折现到某一时间点进行计算，涉及到工程使用寿命、折现率等重要参数。由于资金时间价值的存在，未来发生的成本不能直接累加，必须以适当的折现率将各项成本折现到计算时点。

综上所述，建筑工程全生命周期成本分析与工程结构可靠度、工程使用年限、折现率、运营维护成本、建设成本等数据有关。其中，工程结构可靠度直接决定了工程使用年限的长短。建筑LCCA中折现率的取值也尤为关键，《建设项目经济评价与方法参数》(第三版)中给定的社会折现率为8%[8],如此高的折现率会将未来现金流量折现殆尽，不利于运营维护成本的计算，建议结合当地经济发展水平采用分时段分区域递减折现率进行计算。如我国东部经济发达地区宜采用的折现率为5%～6%(计算周期n为1～10年时段)、4%(n为11～21年时段)、3%(n为22～43年时段)、2%(n为44～90年时段)、1%(n大于90年时段)；中部区域较发达区域宜采用的折现率为7%～5%(n为1～14年时段)、4%(n为15～26年时段)、3%(n为27～47年时段)、2%(n为48～95年时段)、1%(n为大于95年时段)；西部欠发达地区宜采用的折现率为6%～8%(n为1～10年时段)、5%(n为11～17年时段)、4%(n为18～28年时段)、3%(n为29～50年时段)、2%(n为51～100年时段)、1%(n为大于100年时段)[9]。

2.2 基于结构可靠度的建筑LCCA模型

式(1)是结合结构可靠度劣化及维修方案的成本构成来划分的，每个成本构成子项都与结构可靠度相关联，可与结构可靠度建立成本函数关系。初始建设成本与结构可靠度之间的关系模型[10]如式(2)所示，该公式主要用于描述结构可靠度提高与建设成本增加之间的关系，可用于初步设计阶段多方案结构可靠度的选择，不适用于初始造价的计算，初始造价计算需结合建筑施工图、结构施工图计算出工程量后进一步套取价格计算。

(2)

式中:Ps为工程结构可靠度，其值大约在0.996 533～0.999 979之间；α为无量纲参数,α=hCc0(h为结构投资收益率的平均值，可由既有建筑统计得到)；Cc0为结构趋于失效时的工程造价。

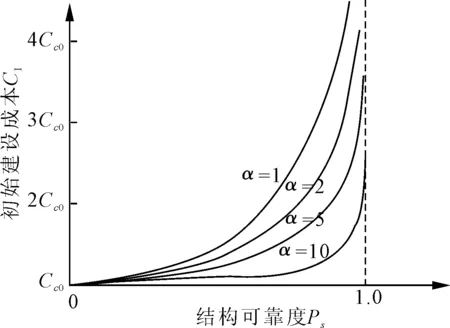
图1 结构可靠度与工程初始建设成本的函数关系

初始建设成本与结构可靠度的函数关系如图1所示，其中Cc0为可靠度趋于0时的工程建设成本，曲线趋势完全由α决定。当结构可靠度不大时，提高工程结构可靠度所需增加的建设成本较小，随着程结构可靠度的增大，需增加的建设成本越高，可见一味地追求高结构可靠度会带来高建设成本，对当前投资决策方案选择不利，结构可靠度的选择应结合当前经济和社会环境来决定。

工程检测成本和工程预防性维修成本统称为工程日常检测维护成本。检测精度越高，越能检测出工程所存在的问题，进而有利于降低维护成本。检测成本与结构失效损失、检测时间密切相关，结构失效损失越大，检测成本则越高。检测数据越可靠、检测方法越科学，则越能够检测到结构的损伤情况，据此制定科学的维护措施以延长结构使用寿命。检测时间间隔越长，越不利于结构失效的检测。工程预防性维修即日常维修，可以缓解工程结构劣化速度，延长工程使用寿命，但不能改变工程结构可靠度。预防性维修仅适用于当工程结构可靠度较高、劣化速度较快时，可以缓解工程劣化速度。依据工程资金等值计算原理，推导出日常检测维修成本和工程加固维护成本的计算公式，分别如式(3)和式(4)所示。

(3)

CREP=J·(1+i)-T1

(4)

式中:CINFM为工程日常检测维护成本；B为单次检测维护成本；nf为工程检测维护次数,若T/f的余数不等于0，则nf=int(T/f)，否则nf=T/f-1；T为工程结构使用寿命；f为检测维护成本发生间隔时间；J为单次工程维修加固成本；T1为维修加固的时间即为结构开始劣化的时间。

对于不需要维修的工程来说，加固维护成本为0。而是否需要对既有建筑进行维修加固取决于维修加固所取得经济效益与维修加固成本之比,若两者比值大于1，则可以采取维修加固措施，以提高结构可靠度，进而延长结构使用寿命，否则可不采取加固措施。

工程结构失效会造成直接损失成本和间接损失成本，结构失效损失成本与结构破坏等级具有直接关系，结构失效损失程度可依据专家评估划分为完好、轻微、中等、较严重、严重5个等级。依据不同的结构失效损失程度可将工程结构失效成本的计算模型定义为：

CFALL=(CF1+CF2)·pf·(1+i)-T

(5)

式中:CF1和CF2分别为结构的直接经济损失和间接经济损失；pf为失效概率，结构失效概率可查询《建筑结构可靠性设计统一标准》得到；T为工程结构使用寿命;i为折现率。

综上所述，结合前文各成本的计算公式可将式(1)扩展为：

(CF1+CF2)·pf·(1+i)-T

(6)

2.3 结构可靠度、工程使用寿命和LCC之间的函数关系分析

在项目方案设计及施工阶段，钢筋混凝土结构的初始可靠度直接影响着建筑方案的全生命周期成本，结构初始可靠度Ps越高初始建设成本则越高，过高的结构可靠度带来的高建设成本不利于项目方案在工程设计阶段的方案比选。在项目运营维护阶段，需要对建筑进行维护，分为正常的日常维护和维修加固两类。正常的日常维护是为了保障工程的基本性能，属于例行保养，不能改变工程的结构可靠度，而维修加固则可以提高工程的结构可靠度，延长工程的使用寿命和提高结构安全性[11]。基于结构可靠度的全生命周期成本计算原理如图2所示。

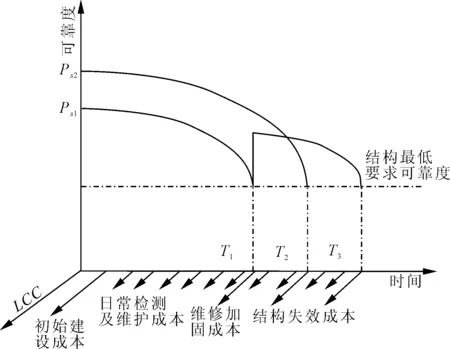
图2 结构可靠度、LCC和结构使用寿命关系图

由图2可知，当结构可靠度由Ps1提高到Ps2时，将使得初始建设成本增加，当工程使用到T1时点时对结构采用维护加固措施，会使得结构的工程使用寿命延长到T3，但是会增加运营维护阶段成本。如果结构初始可靠度维持在一个较高的水平Ps2，初始建设成本会增加，其结构使用寿命在没有任何维修加固干预措施的情况下可以达到T2的水平，结构可靠度、LCC和工程使用寿命三者之间息息相关，应建立三者之间的函数关系来考量。

设定T为工程结构使用寿命，T1为工程结构劣化开始时间，β0为结构初始可靠度指标，无维修时的可靠度指标劣化率为A，根据我国《建筑结构可靠性设计统一标准》(GB50068-2018)，一级结构性破坏的目标可靠度指标β=3.7，则结构的失效概率pf=1.078×10-4。结构可靠度指标函数与3个变量之间的关系为:

(7)

设定最低可靠度指标β*=0.85，β(t)=0.85，β=3.145，将该参数代入式(7)可得工程结构使用寿命与结构可靠度的计算公式：

T=T1+(β0-3.145)/A

(8)

将式(8)代入式(6)可得建筑全生命周期成本、结构可靠度及工程结构使用寿命三者的成本关系函数。

3 基于结构可靠度的建筑LCCA流程

结合前文分析，基于结构可靠度的建筑LCCA流程如图3所示。

建筑全生命周期成本分析流程分为决策、设计、施工及运营维护4个阶段。4个阶段的信息可借助BIM模型进行管理和存储，将建筑实体信息、项目环境信息、安全知识信息都存储于BIM数据库中，建筑实体信息主要包括建筑结构尺寸、材料信息等[12]。借助BIM平台为建筑可持续设计提供充分的数据保障，决策阶段和设计阶段应以可持续设计理念执行全生命周期成本分析方法进行规划和设计。决策阶段拟定结构可靠度并进行LCC初步核算为设计阶段提供基础数据，将决策阶段LCC核算结果作为设计阶段LCC概算的最高限额。设计阶段从全生命周期成本分析的角度执行可持续设计，依据结构可靠度设计工程使用寿命与目标可靠度水平，优化结构耐久性设计，进行耐久性设计加强及防护，开展运营维护阶段的检测维护方案设计，并依据方案数据预测工程检测维护成本和工程失效成本。施工阶段主要对各类设计参数进行控制并及时反馈给设计单位，同时重点控制施工成本使之不超过设计概算。运营维护阶段依据结构初始可靠性能预测结构劣化速度，定期进行检测和维护，将检测维护数据传递给运营维护中心，运维中心依据数据核算结构剩余使用寿命及工程结构失效时间并做出维修加固决策。

图3 基于结构可靠度的建筑LCCA流程

4 案例分析

4.1 工程背景

我国东部某三线城市一单位主楼建于2001年，为钢筋混凝土结构，总建筑面积约2.5万m2，该市月平均租金为20元/m2。对结构破坏主要由混凝土炭化后的钢筋锈蚀引起，为一级结构延性破坏，根据我国《建筑结构可靠性设计统一标准》，一级结构性破坏的目标可靠度指标β=3.7。现需对该工程进行维护改造，有两种方案，要求从全生命周期成本分析的角度选择最优方案。

4.2 甲、乙方案数据

甲方案通过设计单位测算，计划将未来结构劣化开始时间T1控制在10年，可靠度指标劣化率A为0.03。甲方案改造工程初始造价为1 400万元，单次日常检测维护成本为30万元，检测周期为每6年检测一次，即f=6年，经过改造后预测初始可靠度指标值β0为3.7。

乙方案计划提高初始可靠度指标，降低可靠度指标劣化率，以延缓改造后该工程的劣化速度。设计单位预测该方案可使得改造后结构初始可靠度指标β0=4.0，改造后工程结构劣化开始时间T1为20年，可靠度指标劣化率A=0.025。乙方案改造初始工程造价为2 400万元，单次日常检测维护成本为30万元，检测维护周期为5年，即f=5年。

假定此次改造后不再对工程进行大规模维修加固，则工程使用时间到达劣化开始时间T1后，两方案的维修加固成本均为0。工程直接失效损失成本和间接失效损失成本分别用失效损失系数kF1和kF2来表示，用来确定工程失效损失成本与初始建设成本的系数关系，则直接失效损失成本可以表示为CF1=kF1CI，间接失效损失成本可以表示为CF2=kF1kF2CI，各项参数的取值如表1所示[13]。

表1 结构失效损失等级与各失效损失系数参数表

4.3 折现率选择及工程结构使用寿命计算

该工程位于我国东部，属于经济发达地区，为了不对未来成本造成粗暴折算，同时考虑计算的便利性，依据前文分析取折现率为5%。 依据两方案的数据计算甲、乙方案工程结构使用寿命：

T甲=T1+(β0-3.145)/A=10+(3.7-3.145)/0.03=28.5(年)

T乙=T1+(β0-3.145)/A=20+(4.0-3.145)/0.025=54.2(年)

4.4 两方案全生命周期成本计算及对比

依据表1数据分析计算两方案工程失效损失成本：甲方案工程结构劣化开始时间T1为10年，因此从0到10年时间段甲方案工程失效损失成本CF(0～10)=0,从T1时间点开始结构开始劣化，依据式(5)、式(6)及表1数据计算得到CF(10～28.5)=180万元，则甲方案工程失效损失总成本为180万元。同理可以计算得到乙方案工程失效损失成本CF(0～54.2)=CF(0～20)+CF(20～54.2)=0+360=360万元。

结合式(1)～式(7)计算得到甲、乙方案的建筑全生命周期成本：

0+180×(1+5%)-28.5=1 532.9(万元)

0+360×(1+5%)-54.2=2 467.5(万元)

由于两个方案的工程结构使用寿命差别较大，用建筑全生命周期成本进行比较不具备可比性，因此需进一步将建筑全生命周期成本折算为平均年值:

虽然乙方案的全生命周期成本高于甲方案，但是乙方案的平均每年投入的成本低于甲方案，假设将该主楼出租，则按该市租金水平每年可获得租金2.5万m2×20 元/(m2·月)×12月=600万元，年租金收入要远大于年平均成本，所以乙方案为最优改造方案。

5 结论

笔者以降低建筑全生命周期成本为出发点，将建筑结构可靠度设计与LCCA相结合，系统研究了建筑结构可靠度与全生命周期成本之间的函数关系，并提出了基于结构可靠度的全生命周期成本分析的系统流程，实现了全生命周期成本分析在结构可持续设计中的应用。同时为设计方案决策者进行方案比选提供了具有可操作性的流程，还为建筑的可持续性设计提供了思路和方向。