装配作业车间调度的免疫粒子群算法实现

孙 虎，周晶燕

(武汉理工大学 物流工程学院，湖北 武汉 430063)

装配作业车间调度(AJSS)是生产中常见的生产组织形式，具有复杂的物料清单结构，包含多层装配节点，其生产调度更加有挑战性，相关研究相对较少。为充分利用制造资源，提升企业核心竞争力,有必要对装配车间生产调度进行优化。

目前，学者多采用遗传算法求解AJSS问题，较少见粒子群算法和免疫粒子群算法在这一领域的应用研究。故笔者采用免疫粒子群算法求解最小化最大完工时间的装配作业车间调度模型，综合考虑粒子群算法和免疫算法各自的求解特点，通过多次重复试验验证免疫粒子群算法求解的高效性和实用性。

1 装配作业车间调度

1.1 问题定义

AJSS问题是在调度的初始时刻，知道所有要调度产品的详细信息，包括产品结构和工序详细信息。该问题的优化目标是确定每个工序在每一台机器上的开始时间和完成时间，使得总加工时间最小。

1.2 研究现状

近年来，针对AJSS这一类NP-hard问题，学者们已提出一系列求解该问题的调度算法。如TAVAKKOLI-MOGHADDAM等[1]研究了一个层次化的分支定界算法来解决装配操作的混合流装配作业车间调度问题。TIAN等[2]提出了一种离散粒子群优化算法来解决两阶段装配调度问题。SUNG等[3]利用解的性质给出了一种分支定界算法，来求解两阶段的多机器装配调度问题。 SHOKROLLAHPOUR等[4]研究了一个以最大完工时间和平均完工时间加权和最小化为目标的两阶段装配流程车间调度问题，提出了一种新的元启发式帝国竞争算法。LIAO等[5]研究了N个产品的装配调度问题，将该问题表述为一个混合整数规划模型，并提出了求解最优解的若干性质。MOZDGIR等[6]提出了一种混合变量邻域搜索类电磁机制算法来求解一个两阶段装配流程车间调度问题。WONG等[7]提出了两种拉格朗日松弛技术的混合进化算法，以最小化最大完工时间为目标。AL-ANZI等[8]提出了一种AJSS人工免疫系统，目标是最小化总工时或平均完成时间,并提出了用混合禁忌搜索(TS)启发式算法来求解AJSS问题[9]。

2 粒子群算法模型

首先初始化n个D维粒子的位置与速度，第i(i=1,2,…，n)个粒子的位置为xi=[xi1,xi2,…,xiD]。速度为vi=[vi1,vi2,…,viD],d=1,2,…,D。粒子在飞行过程中不断迭代更新自己的速度和位置，其迭代规则为：

v′id=ωvid+c1r(pid-xid)+c2R(pgd-xid)

(1)

x′id=xid+vid

(2)

式中：c1，c2为常量，通常在0到2之间取值；r和R服从0到1的均匀分布；pi为第i个粒子经历过的具有最好适应度值的位置，记作pi=[pi1,pi2,…,piD]；pg为整个粒子群经历过的具有最好适应度值的位置，记作pg=[pg1,pg2,…,pgD]；ω为惯性权重。这里采用自适应调节，即ω随着迭代次数的增加线性减少：

ω=ωmax-in(ωmax-ωmin)/imax

(3)

式中：ωmax和ωmin分别为ω的初始值与终止值；imax为最大迭代次数；in为当前迭代次数。

3 免疫粒子群算法实现

粒子群算法的一个问题在于容易过早收敛，导致局部最优，免疫算法特有的浓度抑制机制可以防止适应度较高的粒子过度繁殖，帮助维持粒子的多样性，弥补了粒子群算法过早收敛的缺陷。免疫粒子群算法(immune particle swarm optimization, IPSO)就是将两者进行结合的混合算法。

刘国联等[10]针对遗传算法提出了“精英替代”策略，其基本思想是将种群中适应度最低的个体淘汰，用精英个体替代。笔者尝试对免疫粒子群算法做这样的改进，研究其在解决AJSS问题中是否有效，算法简称为EIPSO。

3.1 算法重要参数

(1)种群大小(n)。种群大小指粒子的总数，粒子数目的多少对搜索效率有一定的影响，需要通过实验确定合适的数目。

首先.对于三维欧式空间3的一组不共面的向量e1,e2,e3,我们可以唯一以其作为一组基底构造仿射坐标系.记gij=ei·ej,由于内积的交换性,故

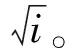
(3)粒子间的距离(distance)。选择Euclidean距离，将粒子x1=[x11,x12,…,x1D]和x2=[x21,x22,…,x2D]的距离定义为：

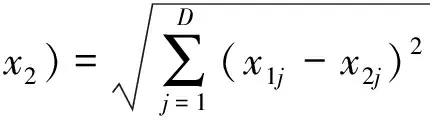
(4)

(4)浓度(density)。粒子的浓度即抗体的浓度，指群体中相似抗体所占的比重。这里设定一个浓度抑制半径σ，取值为0.1，将距离小于σ的粒子看作是相似。粒子浓度的计算公式为：

(5)

(5)激励度(actuation_probability)。激励度这个概念出现在免疫算法中，指抗体群中抗体应答抗原和其他抗体激活的综合能力。

(6)

其中,β取值为2。

(6)选择概率(selection_probability)。选择概率是该粒子(抗体)的激励度占所有粒子激励度的比重：

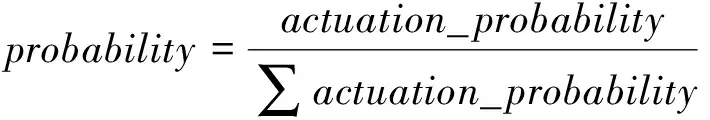
(7)

3.2 编码与解码

某实例的装配作业结构图如图1所示，可知两个装配产品，一共有6个工序。不同工序的加工时间、所需机器如表1所示。

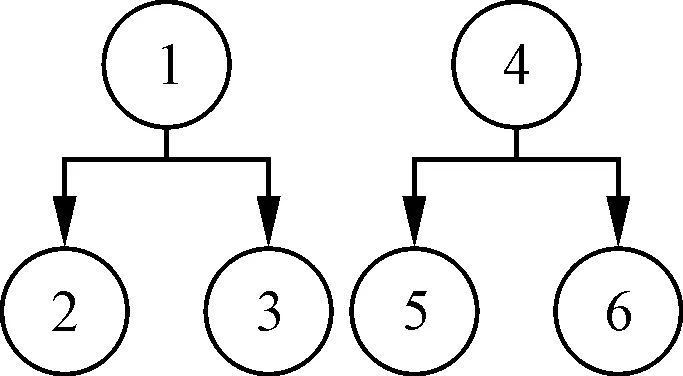
图1 装配作业结构图

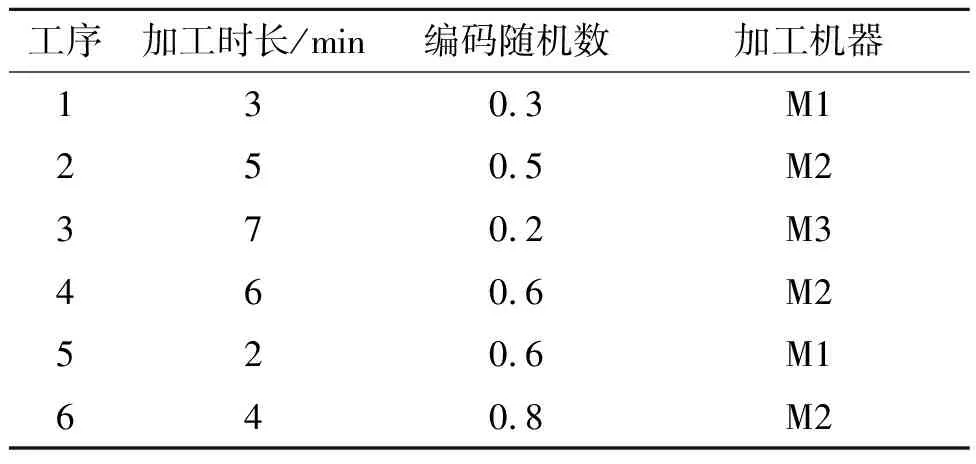
工序加工时长/min编码随机数加工机器130.3M1250.5M2370.2M3460.6M2520.6M1640.8M2

笔者采用随机数编码，对每个工序给一个0～1之间的随机数。这里规定随机数越小表示优先级越大，即粒子的编码为x1=(0.3,0.5,0.2,0.6,0.6,0.8)。

对于解码问题，定义所有前序工序都完成的工序为可调度工序。如对于工序4，只有工序5和工序6都完成时其才为可调度。考虑所有产品的可调度工序，每次从中选取一个随机数最小的优先安排到最早的时间进行加工，重复进行一直到所有工序都被完成。按照这个规则，工序的加工顺序为3、2、1、5、6、4，最终调度结果如图2所示。

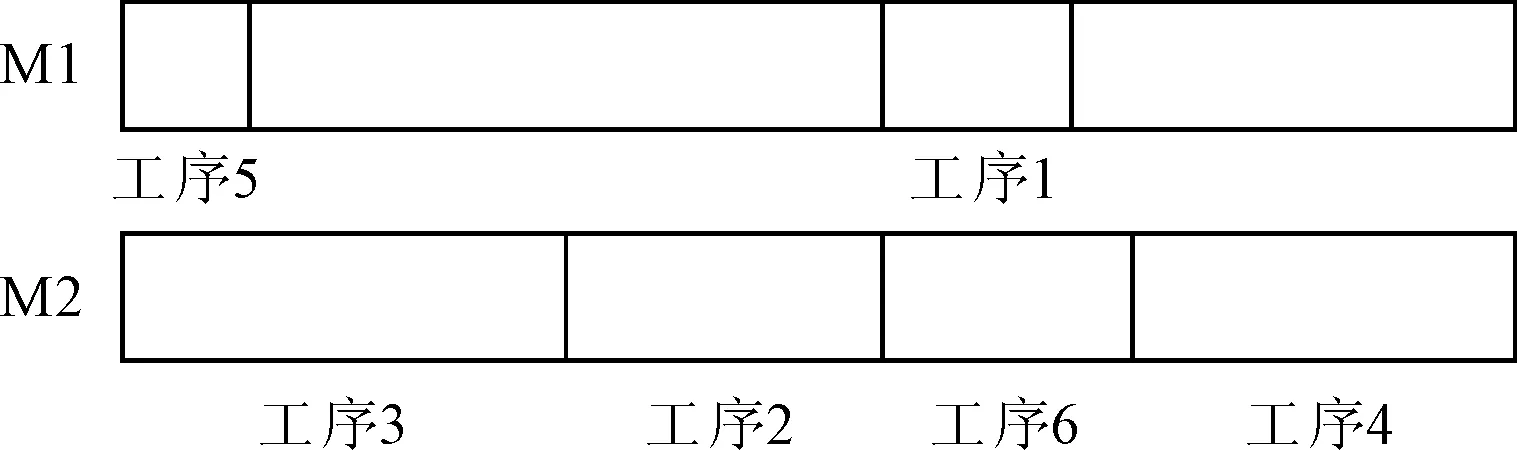
图2 工件加工顺序图

3.3 算法步骤

(1)初始化系统。用户设定相应的参数，随机产生规模为population_size的种群，此为第一代。

(2)基于免疫的选择、交叉、变异更新。根据式(7)，每次选择2个粒子作为父代，交叉变异后得到2个粒子作为子代，从父代和子代4个粒子中选择适应度最好的1个粒子作为下一代。重复population_size次，得到新的种群。

(3)对步骤(2)得到的种群根据粒子群算法进行更新，得到下一代种群。

(4)如果达到循环终止条件，则退出循环，否则返回到步骤(2)。

3.4 算例

算例应用Visual Studi.Net编程实现，比较EIPSO、IPSO和PSO在不同问题规模和复杂度下的表现。系统生成3种不同类型的产品，类型1～3的层级分别为2,3,4，第1～3层的下属分支数分别服从[2-5],[2-4],[2-3]的均匀离散分布。每个分支的工序数服从[1-8]的均匀分布。每个工序的加工时间为均值为1的负指数分布。

3.4.1 重复试验求解

为了在相同条件下比较不同算法，统一设定3种方法的计算时间上限为10 s，交叉和变异概率分别取0.8和0.1。对于每种产品类型，生成6个产品作为一个算例。对于每个算例，种群大小n取5、10、15共3种设定，并采用3种不同的算法计算，一共有3×3=9种设定。

(1)针对最简单的类型1、双层结构的产品，不同设定的求解结果如表2所示，类型1产品不同种群大小结果对比如图3所示，类型1产品不同算法结果对比如图4所示。由于类型1产品相对简单，求解结果差异不大。唯一的例外是IPSO、种群大小为5的情况，取值较差，但绝对数值相差并不大。结合图3和图4可知，其均值数据也反映了这种差异。

表2 类型1产品优化结果表

图3 类型1产品不同种群大小结果对比

图4 类型1产品不同算法结果对比

(2)类型2产品的具体运行结果如表3所示，类型2产品不同种群大小结果对比如图5所示，类型2产品不同算法结果对比图6所示。结合图5和图6可知，当种群大小为15时，算法寻得的当前最优解最好。而在3种算法之中，EIPSO算法寻得的当前最优解最好，PSO算法最差，IPSO居中。

表3 类型2产品优化结果表

图5 类型2产品不同种群大小结果对比

图6 类型2产品不同算法结果对比

(3)类型3产品的具体运行结果如表4所示，类型3产品不同种群大小结果对比如图7所示，类型3产品不同算法结果对比如图8所示。可知当种群大小为15时寻得的当前最优解最好，而在这3种算法之中，EIPSO算法寻得的当前最优解是最好的，PSO算法表现最差。

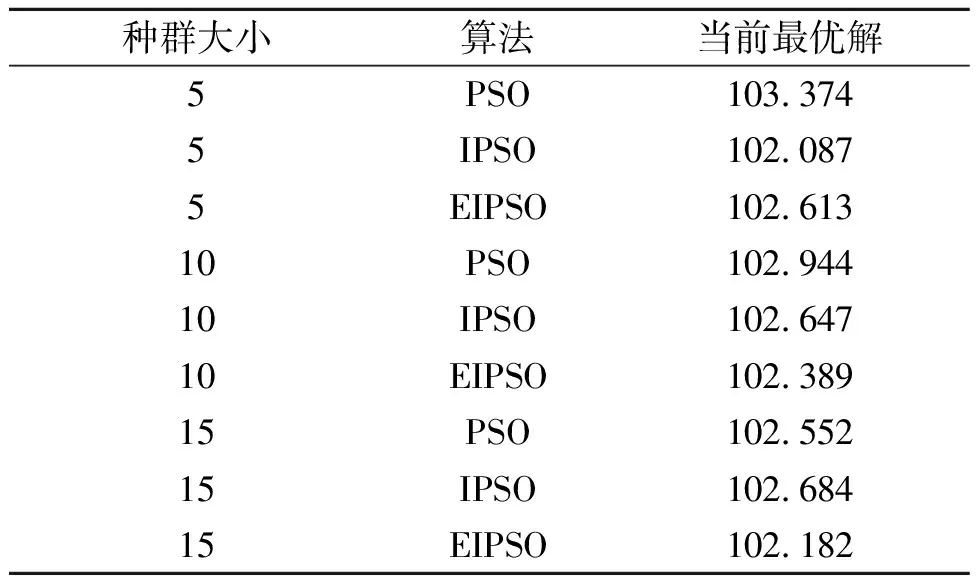
表4 类型3产品优化结果表

图7 类型3产品不同种群大小结果对比

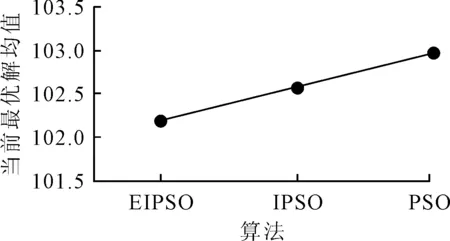
图8 类型3产品不同算法结果对比

3.4.2 算法收敛性分析

由上文可知，在短时间内EIPSO的表现最佳，但是较短的时间不能保证3种算法都达到收敛，因此无法得出定论。故针对不同类型的产品，保持其他参数不变，延长运行时间至100 s进行收敛性分析，重点比较这3种算法解决问题的不同表现。种群大小为上述短时间内不同产品求解的最佳设定，依次为10,10,15。

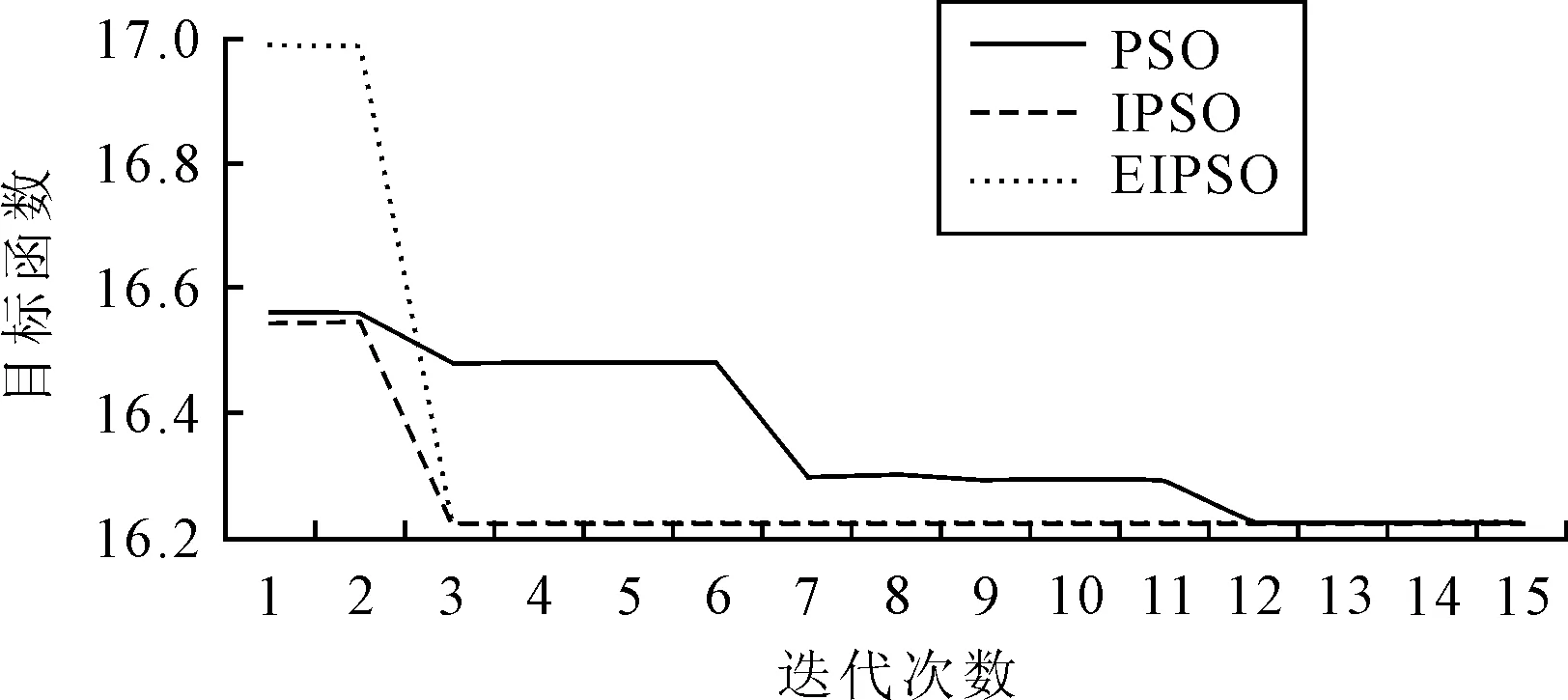
图9 类型1产品优化结果折线图

(1)类型1产品运行结果如图9所示。在100 s内，PSO、IPSO、EIPSO这3种算法分别迭代了2 370次、1 317次、1 315次。其中，PSO在第12次迭代时收敛到了最优值，IPSO和EIPSO在第3次迭代时收敛到了最优值，三者最优值相同。类型1产品的结构比较简单，包含的工序数少，解的搜索空间比较小，所以3种方法基本上都能够迅速收敛到一个值。不同之处在于收敛速度，其中PSO收敛最慢，IPSO和EIPSO收敛速度相似。

(2)类型2产品运行结果如图10所示。在100 s内，PSO、IPSO、EIPSO这3种算法分别迭代了1 818次、773次、777次。其中，PSO在第49次迭代时收敛到了最优值42.974，IPSO在第11次迭代时收敛到了最优值42.965，EIPSO在第175次收敛到了最优值42.965。IPSO和EIPSO最后找到的最优值相同，都好于PSO的最优值。另外，值得注意的是，IPSO在这个例子中比EIPSO收敛得更快。

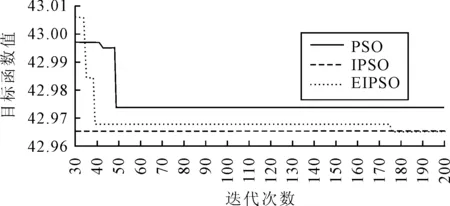
图10 类型2产品优化结果折线图

(3)类型3产品运行结果如图11所示。在100 s内，PSO、IPSO、EIPSO这3种算法分别迭代了790次、352次、370次。其中,PSO在第66次迭代时收敛到了最优值103.025，IPSO在第246次迭代时收敛到了最优值102.079，EIPSO在第37次收敛到了最优值102.163。可以看出，PSO表现最差，EIPSO次之，IPSO最好。

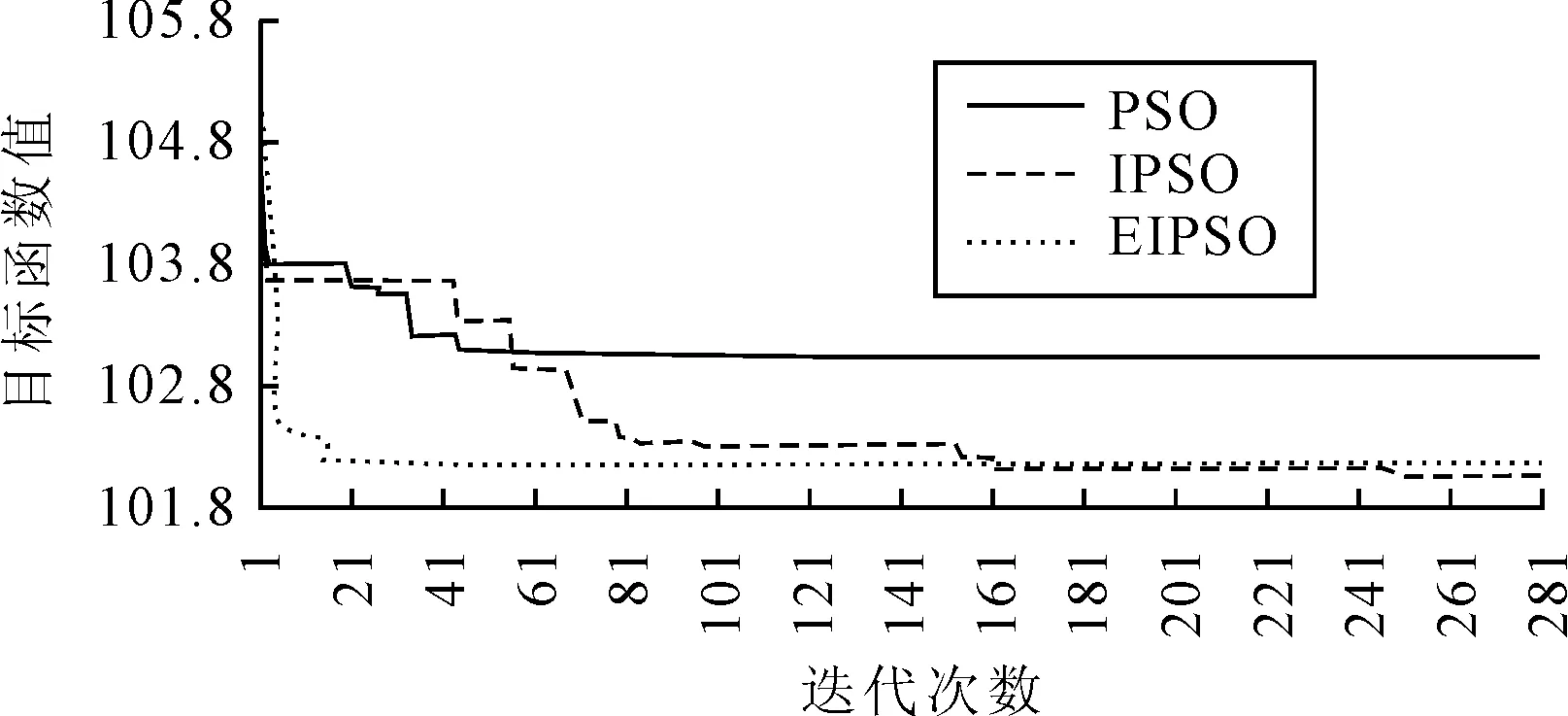
图11 类型3产品优化结果折线图

4 结论

作业车间调度问题是现代制造业技术的基础，而装配环节更是产品制造中不可或缺的部分。笔者通过设置多次的重复试验求解AJSS问题，证实了免疫粒子群算法求解装配作业车间调度问题的实用性和有效性。研究还发现：对于相对简单的产品，PSO与两种基于免疫的算法(IPSO、EIPSO)的差别比较小；但是对于规模较大(类型3)的产品，IPSO比PSO更好地避免早熟，得到的结果也更好。如果给定比较合理的搜索时间，IPSO和EIPSO基本上都能够找到比PSO更好的解。

在收敛性分析中，针对免疫粒子群算法加入“精英替代”策略的改进问题，由于“精英替代”策略减少了粒子的多样性，导致EIPSO比IPSO更容易陷入局部最优解。因此，在未来的研究中，如何权衡“择优”与“保留粒子多样性”仍是一个值得深入探索的问题。