基于符号网络的社团检测

刘鹏翼

（山西金融职业学院信息技术系，太原 030008）

0 引言

相比于普通复杂网络只能表示节点之间有无关系，符号网络可以表示节点之间的正负关系从而可以隐含更多信息[1]。许多现实世界的系统可以用符号网路来表示。例如，在在线社交网络中，节点之间的正关系可以表示“赞同”、“朋友”。节点之间的负关系可以表示“反对”、“敌人”。

许多社交网络已经被发现具有社团结构。在普通的复杂网络中，社团结构表现为同一社团内的节点之间的联系比不同社团间节点间的联系更加紧密。而符号网路因为节点间负关系的存在使得社团结构更加复杂。它表现为同一社团内部节点多为正连接，不同社团节点间多为负连接。用来发现这种社团结构的社团检测是社交网络分析（Social Network Analysis，SNA）最重要的任务之一。在过去一段时间，虽然有各种各样的社团检测方法被提出，但是他们大多数都是基于普通复杂网络的[2-4]。虽然近几年也有一些基于符号网络的社团检测方法被提出，但是它的发展依然很有限。

在本文中，基于符号网络中存在负关系的特性，我们巧妙地将符号网络分隔为正负两个分量。然后在正负两个分量上分别利用非负矩阵分解进而得到符号网络的社团结构。我们在人工生成的数据集上进行了实验。验证了我们的方法具有很高的有效性和准确性。

1 符号网络社团检测方法

近几年，一些符号网络社团检测的方法被提出。这些算法可以大致分为以下几类：基于平衡理论、基于符号模块度优化、基于生成模型。

1.1 基于平衡理论

二十世纪四十年代，Heider[5]基于个体的感知和态度提出了结构平衡理论，这是关于符号网络最重要的社会理论基础。五十年代，Cartwright和Harary[6]进一步在图模型的基础上发展了结构平衡理论。结构平衡理论应用在符号网络中的主要内容是：在符号网络中，社团内部节点间的联系多为正关系，不同社团节点间的联系多为负关系。相对应与符号网络中结构平衡理论的内容，提出了符号网络中噪声的定义，即社团内部节点间的负关系和不同社团节点间的正关系。随后基于平衡理论的思想许多符号网络社团检测的方法被提出。Doreian P、Mrvar A提出了一个最小化符号网络噪声的方法[7]来进行符号网络的社团检测。Bansal等人提出了一个Correlation Clustering（CC）的方法[8]来最大化社团内节点正关系和不同社团节点间负关系进而对符号网络进行社团检测。相似地，Larusso等人[9]运用相同的思想进行符号网络社团检测。Traag[14]基于平衡理论扩展原有的Potts模型结合符号网络中的负连接来挖掘符号网络的社团结构。

1.2 基于符号模块度优化

标准模块度是基于普通复杂网络的。它度量了网络中实际的连接与随机连接的偏离程度。普通复杂网络的社团结构可以通过优化标准模块度目标函数得到[11]。但它的求解实质是一个离散组合问题[10]。即NP-hard问题。所以可以通过一些启发式算法来求解，例如模拟退火算法。Gomez S[12]通过模块化重构来分析普通复杂网络的社团结构。而符号模块度是由Li Y[13]通过改进标准模块度来定义的，使符号模块度可以处理符号网络中负关系的情况。符号模块度通过调节符号网络正负分量上权重来平衡节点间正连接形成社团和节点间负连接破坏社团的趋势。它本质上是标准模块度的加权融合，所以它的求解同样属于NP-hard问题。对此一些优化算法被提出。例如，Anchuri和Magdon_Ismail基于普通复杂网络模块度优化的算法[11]扩展提出了一个谱聚类[15]的方法来进行符号网络社团检测。

2 基于生成模型

以上的基于符号网络的社团检测都是基于优化目标函数或者启发式的方法，并不关心网络的生成。所以一些基于生成模型的算法被提出。例如，Yang等人[16]提出了一个基于代理的随机游走模型（FEC）来挖掘符号网络中的社团结构。Zhao等人[17]提出了一种概率模型（SISN）来对符号网络进行建模，并推导出基于期望最大化的参数估计方法来挖掘符号网络中的社团结构。Chen等人[18]提出了一个重叠社团检测方法-符号概率最大化模型（Signed Probabilistic Mixture，SPM）。Jonathan Q.Jiang提出了一个广义随机块模型（Stochastic Block Model，SBM）[19]，通过将表现出相似的正负连接轮廓的顶点分组到同一簇中来探索符号网络的介观结构。Yang等人[20]提出的符号随机块模型（Signed Stochastic Block Model，SSBM）。基于一种随机的观点生成连接的密度和符号，刻画并生成符号网络的块结构，并基于变分贝叶斯进行优化，自动确定社团个数。

然而上述的方法社团检测的结果的准确性上都不是很高。为此我们基于非负矩阵分解的思想提出了一个新的符号网络社团检测的方法。

3 研究与改进

3.1 非负矩阵分解

非负矩阵分解作为无监督学习中最受欢迎的方法之一由Lee D D在1999年[21]提出并广泛应用在网络分析中。利用非负矩阵分解在普通复杂网络中的社团检测可以表示为：

A表示为具有n个节点的普通复杂网络的邻接矩阵，H表示节点的指示矩阵，每个元素Hir表示了第i个节点在社团r中的可能性，W代表基矩阵。

3.2 改进

由于符号网络中存在负关系，不能直接应用非负矩阵分解在符号网络中。我们巧妙地将符号网络分解为正负两个分量。给定一个符号网络G，它的邻接矩阵A可以分解为正分量邻接矩阵A+和负分量A-。其中A=A+-A-。W+和W-分别为正分量和负分量上的基矩阵。H表示节点的指示矩阵，每个元素Hir表示了第i个节点在社团r中的可能性。

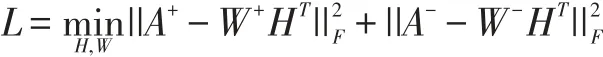
算法步骤

符号网络社团检测非负矩阵分解算法

输入

符号网络G的邻接矩阵A；

迭代次数iter；

社团个数k；

输出：

节点指示矩阵H

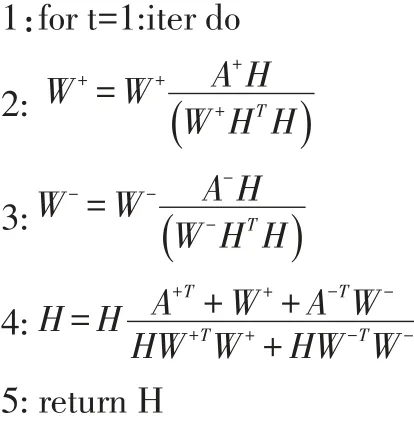
4 实验

4.1 数据集

我们通过人工生成了符号网络数据集，其中包括了以下几个参数 c、n、pin、p+、p-、c是社团个数，n 网络中节点的个数，pin是社团内节点连边的可能性，p+、p-分别表示了社团内部节点间负连接的比例和不同社团节点间正连接的比例（代表了符号网络中的噪声）。我们设置数据集中的参数如下并生成了两种符号网络：c=4，n=128。

（1）无噪声符号网络：pin从0.2到1逐渐增加，p+=0，p-=0；

（2）噪声逐级增大：pin=0.8，p+从 0 到 0.5，p-从 0到0.5；

4.2 评价指标

我们利用归一化互信息（Normalized Mutual Information，NMI）去评价我们提出方法的性能[A.Strehl and J.Ghosh,Journal of Machine Learning Research 3,583（2002）.]。

Where C和C’分别表示了真实社团划分和算法得到的社团划分，k是社团个数，n是节点个数，nij表示了真实在第i个社团被算法划分到第j个社团的节点个数，ni（1）表示了真实在第 i个社团的节点个数，nj（2）是算法得到的社团划分中第j个社团中的节点个数。NMI介于0到1之间，值越大表明算法的性能越好。

4.3 实验一（无噪声符号网络数据集上）

我们将提出的方法同以前的一些算法在无噪声符号网路上（符号网络中相同社团内只有正连接，不同社团间只有负连接）进行了对照实验（如图1），表明我们的方法要更优于之前的一些算法。

4.4 实验二（噪声逐渐增大符号网路数据集）

我们通过控制社团内部节点间负连接的比例p-和不同社团节点间正连接的比例p+来控制符号网络中的噪声。增大符号网络中的噪声并于其他以前的算法（SSL、SISN、FEC）进行对照实验（实验结果如图 2），表明我们提出方法的鲁棒性要优于其他算法。

图1

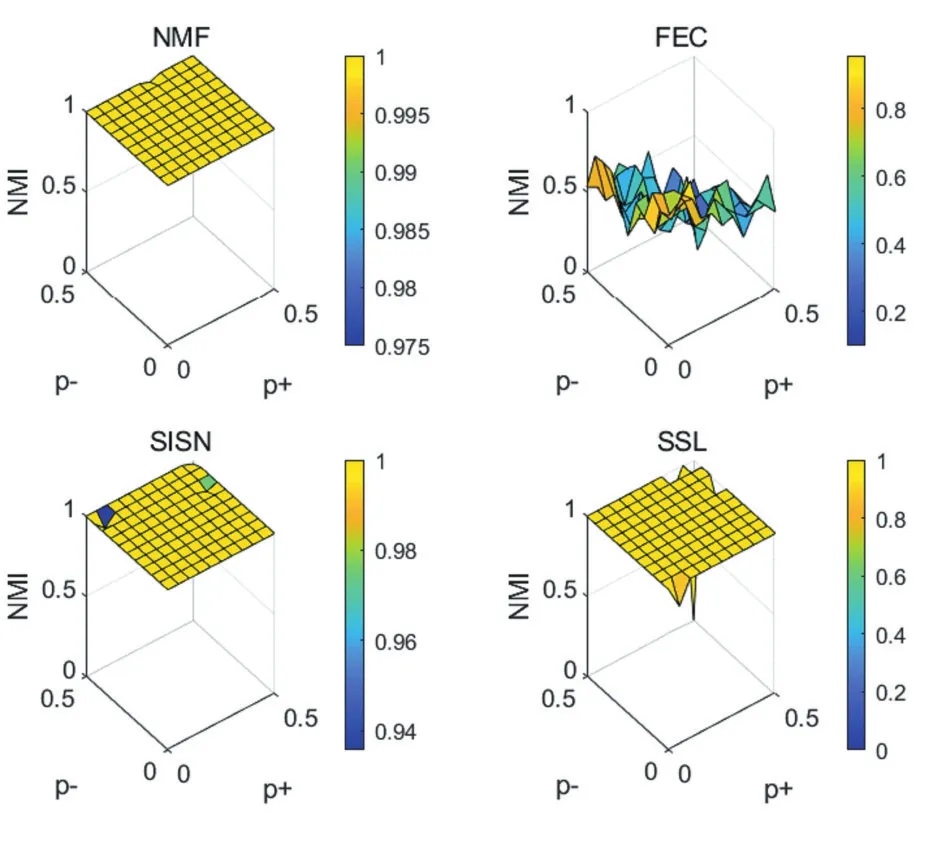
图2

5 结语

在本文中，我们将非负矩阵分解的思想运用到符号网路的社团检测中。巧妙地将符号网络转化为正负两个分量，分别对两个分量进行非负矩阵分解从而得到符号网络的社团结构，在不同性质人工生成的符号网络上的与其他算法的对照实验也证明我们提出方法性能优于之前的一些算法。有着很好的准确性和鲁棒性。未来我们将进一步应用该算法在真实的符号网络数据集上，例如构建新浪微博等在线社交网络的符号网络，挖掘微博网络等在线社交网络的社团结构。