基于梁理论的涡轮冷却叶片蠕变计算

李锦红，张 勇，张如刚，章 胜

(中国航发湖南动力机械研究所，湖南株洲412002)

1 引言

随着航空发动机技术的发展，发动机的工作温度越来越高。特别是其中的燃气涡轮转子叶片[1]，在工作中承受很大的热负荷和机械负荷，蠕变损伤成为涡轮叶片的一种主要失效形式，短时强度的设计理念已无法满足涡轮转子叶片的使用要求。因此，对涡轮转子叶片进行准确的蠕变分析，对其设计具有重要意义。

目前，国内外比较广泛应用的是利用损伤原理，将材料不同工况下的蠕变曲线转化为不同温度下的等效等时应力应变曲线进行三维弹塑性有限元计算[2-4]。该方法可利用有限元分析软件较为简便地模拟冷却叶片的复杂结构，但仅能计算蠕变行为的前两个阶段，且每个温度下只能有一条等效等时应力应变曲线，这与材料的实际蠕变行为不符。部分学者引用多轴时间硬化理论[5]，依据Prandt-Reuss塑性流动法则将单轴的θ模型方程扩展为多轴形式，并将其编写成UMAT用户子程序，嵌入到Abaqus有限元软件，对涡轮冷却叶片进行三维蠕变计算。该方法引用θ参数可较准确地描述材料的蠕变行为，但未考虑蠕变对应力的影响，且其计算极其繁琐。

本文以梁理论为基础，将三维叶片简化为二维截面的叠加，采用累积损伤理论及材料的拉逊-米勒曲线方程计算各截面在不同工况下的等效应力，然后结合给定工况的持久时间和温度，利用实测材料的蠕变曲线进行线性插值计算截面的平均蠕变应变，最后对各截面及各工况的蠕变伸长量进行叠加。该方法直接利用材料的蠕变曲线插值，不仅可计算蠕变行为三个阶段[6]的蠕变应变，而且还可考虑同温度下不同应力对蠕变行为的影响。

2 基本原理与方法

高温下金属材料的组织结构对材料的蠕变特性影响很敏感，蠕变力学特性比较复杂，同一温度下存在多条随时间变化的蠕变应变曲线(图1)，当温度一定时蠕变应变εc为应力σ和时间t的函数：

图1 同一温度下材料的蠕变曲线Fig.1 Creep curve at the same temperature

一般认为，多维应力状态下的蠕变公式必须能退化成正确的一维蠕变计算公式[1]，因而需要将图1中的多维蠕变曲线转化为一维蠕变曲线。

高温下，在恒定载荷作用时间tΣ内，材料的应力并非一定值，为此引入等效应力σequiv的概念。恒定载荷在作用时间内的等效应力表示为：

式中：m为随温度变化的持久强度指数。同一温度下，对金属材料有常数，其中σr为持久强度(MPa)，t为σr对应的持久时间(h)。

σequiv在tΣ时段是恒定的，其引起的损伤相当于在相同时间内随时间变化的实际应力造成的损伤。当温度一定时，蠕变应变与应力及时间的关系可转化为：

式中：q为给定试验条件(温度T，tΣ)对材料造成的损伤，其表达式为

由拉逊-米勒曲线可知，σequiv与其在某一温度下对应的持久时间t的关系为：

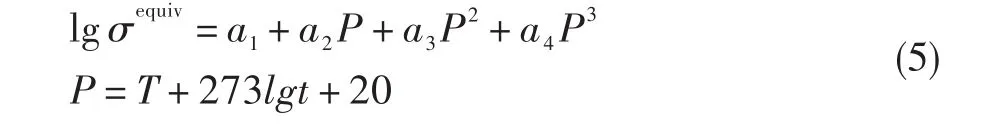
式中：a1、a2、a3、a4可由材料的拉逊-米勒曲线(图2)方程得到。

图2 拉逊-米勒曲线Fig.2 The Larson-miller curve

3 等效应力计算

按照平截面的假设，叶片横截面任意点的纵向变形，是由弹性变形εe、塑性变形εp、εc和因叶片截面不均匀温度场而引起的热变形一起叠加的结果，即截面的应变为：

式中：α为线膨胀系数，ΔT为温升。

由梁理论可知，在平行于叶片截面的x-y平面上，叶片截面的应变为：

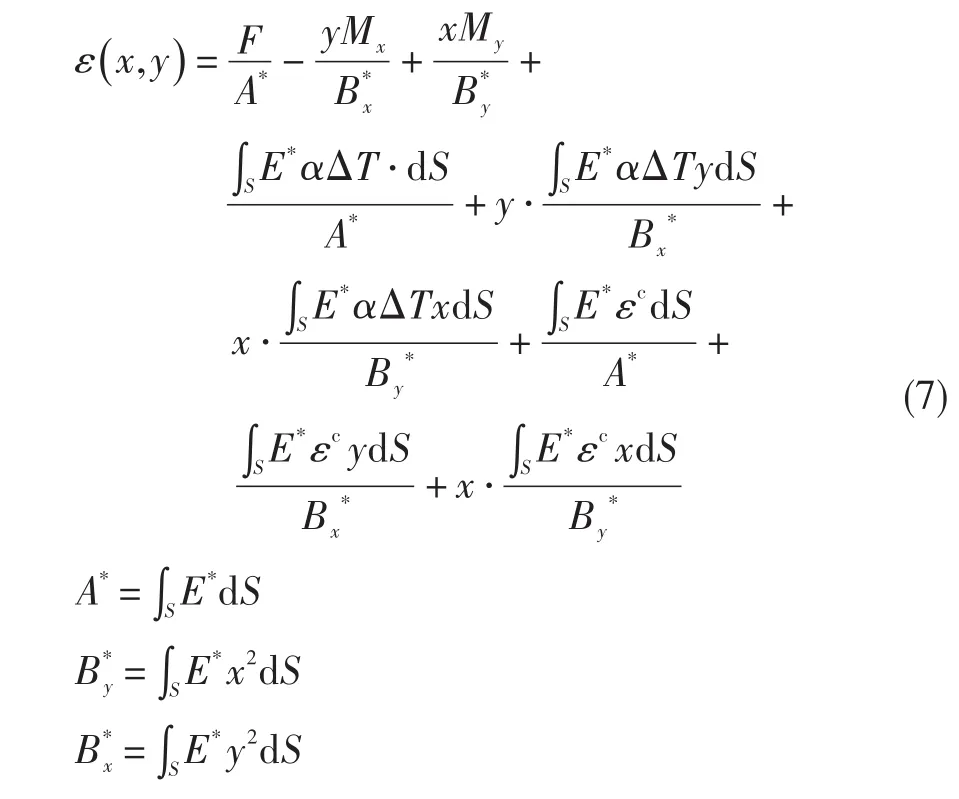
式中：F为叶片截面上的法向力合力，Mx为相对于y轴的弯矩，My为相对于x轴的弯矩，S为叶片截面面积。

考虑应力松弛后，应力为：

蠕变应变εc随时间的变化规律可用蠕变变化率描述。此处引入Lemaitre应变等价原理，单轴损伤蠕变变化率为：

由蠕变试验可看到蠕变模型在变形前后体积不变[1]。本文假设多轴蠕变与单轴蠕变规律相当，则多轴状态下的蠕变变化率为：

将载荷作用时间离散为若干时间步，每一时间步长为 Δti(i=0,…,k)。

(1) 当i=0时，εic=0，根据式(7)和式(8)可计算该时间步下的等效应力σ(Δti)。(2) 当i=i+1时，由式(5)可知σ(Δti)在给定温度条件下的持久时间为t，造成的损伤q=Δti+1/t，根据式(10)，蠕变应变，根据式(7)和式(8)可计算该时间步下的等效应力σ(Δti+1)。

通过以上计算可得到每个时间步下的等效应力，根据式(2)可得到载荷作用时间段的等效应力。

4 计算实例

以某航空发动机燃气涡轮工作叶片为例，用上述方法计算涡轮工作叶片持久试车试验后的蠕变变形。根据飞行包线，该持久试车可划分为5个工况。本文忽略加卸载过程的加减速，认为每个工况内的载荷恒定。

4.1 计算模型

该涡轮工作叶片为铸件，各工况下的持久试车时间见表1。

表1 持久试车时间Table 1 Time of endurance test

将涡轮叶片沿径向平均分为n段，第n段对第n截面提供离心拉力及弯矩。其中第1截面为叶根截面，第n+1截面为叶尖截面，如图3所示。

图3 涡轮叶片截面划分Fig.3 Turbine blade section division

本次计算中n=9，考虑同一截面中相邻节点之间的影响，取整个截面的平均载荷进行计算，结果见表2。

4.2 涡轮叶片

根据文献[7]，当T≥0.5Tm(Tm为材料熔点温度)时，蠕变变形达到不可忽略的程度。本文忽略50%及以下熔点温度的蠕变变形。通过MATLAB对给定的多轴蠕变曲线进行多维拟合，再将表2数据带入进行多维线性插值，计算得到该涡轮叶片各截面各状态下的平均蠕变应变见表3。

表2 各截面的平均温度及等效应力Table 2 Average temperature and equivalent stress of all sections

表3 各截面不同状态下的蠕变应变Table 3 Creep elongation on different sections under different conditions

经过5个工况后，该涡轮工作叶片各截面的平均蠕变应变见表4。

表4 各截面蠕变应变Table 4 Creep elongation on each section

本文认为，叶尖截面的蠕变应变为0，相邻截面的平均蠕变应变为对应叶片段的蠕变应变，则相邻截面对应段的蠕变伸长量为：

式中：hn为截面n的径向高度(mm)。

该涡轮叶片的蠕变伸长量为：

根据以上公式，计算得到该叶片叶尖的平均蠕变伸长量为0.37 mm。

4.3 与试车结果的对比

表5 计算结果与持久试车结果的对比Table 5 Comparison between calculation results and endurance test results

表5为本文计算结果与发动机持久试车结果对比。由表中可知，持久试车涡轮叶片的蠕变伸长量分散性较大，本文计算结果与持久试车结果的平均值相对误差为14.0%。误差原因主要为：试验结果为叶尖变形的最大值，其结果包括涡轮叶片工作过程中的塑性变形，本文提出的方法未考虑塑性变形，且计算结果为叶尖截面的平均蠕变伸长量。

5 结论

提出了一种基于梁理论的蠕变计算方法，并用该方法对某航空发动机燃气涡轮工作叶片持久试车试验在经过5个工况后的平均蠕变伸长量进行了计算。主要结论为：

(1)本文提出方法在温度梯度较小且单纯考虑蠕变伸长量时具有参考价值。

(2)持久试车涡轮叶片的蠕变伸长量分散性较大，本文提出的计算方法依赖于实测蠕变曲线的置信度，其计算结果在实测蠕变曲线的置信区间内精度更高。

(3)表3计算结果为线性插值得到，部分状态存在外插，对计算精度有影响。

(4)本文提出的方法已应用于多种型号发动机研制中，被证明为适用性较好、工程应用性较强。