含逆变型分布式电源的配电网正序和商阻抗纵联保护
雷 霖,唐成达,张 鹏,赵永鑫,赖真良
(1.西华大学电气与电子信息学院, 四川 成都 610039;2.成都大学信息科学与工程学院, 四川 成都 610106)
随着新能源的日益发展,电力工业出现了由传统大规模集中式供电模式向集中式与分布式相结合的过渡。电力系统中DG渗透率的升高,使传统的配电网保护方案面临严峻考验[1]。目前,关于含DG的配电网保护研究[2-8]较多。文献[2-3]通过限制DG的准入容量,利用故障后电流幅值的差异,构造了新型纵联保护方案。这类保护方案都是以系统稳定状态为前提,并未考虑系统故障等特殊状态,因此得到的准入容量偏于乐观。文献[4-5]分别根据配电网树状结构和DG“T”接线结构特征,提出了自适应保护原理及实现方案。自适应保护方案需要实时检测配电网结构,不能应用于多DG接入的配电网。文献[6-8]构造了故障区段定位的数学模型,并采用和声算法、遗传算法对其进行求解,从数学角度解决故障定位问题。这类保护方案需要处理大量的数据,对主站要求高,并且需要实时上传大量数据,对通信的要求高。
为防止DG大规模脱网事故的发生,现阶段并网标准对分布式电源的低电压穿越能力提出了要求,使含DG的配电网保护更加复杂[9]。由于IIDG在系统故障时可等效为仅存在于正序网络中的压控电流源[10],文献[10-12]提出了基于正序故障分量的保护原理。文献[10]借鉴电流差动保护标积制动特性,提出了带制动特性的正序阻抗纵联保护方案。文献[11]利用母线正序电压故障分量与各馈线正序电流故障分量的相位特征实现故障定位。文献[12]设计了由相量测量单元和数字继电器构成的数字通信系统,提出了一种基于正序分量的保护策略。然而,IIDG的故障特性较为复杂,上述保护方案可靠性仍有待研究。
本文分析了线路区内与区外故障时,线路两端正序电压相量之和与正序相量电流之和的比值特点,提出了一种基于故障正序分量和商阻抗的纵联保护新原理,并使用PSCAD/EMTDC建立仿真模型对新原理进行了验证。
1 正序和商阻抗保护算法的原理
1.1 正序和商阻抗的概念
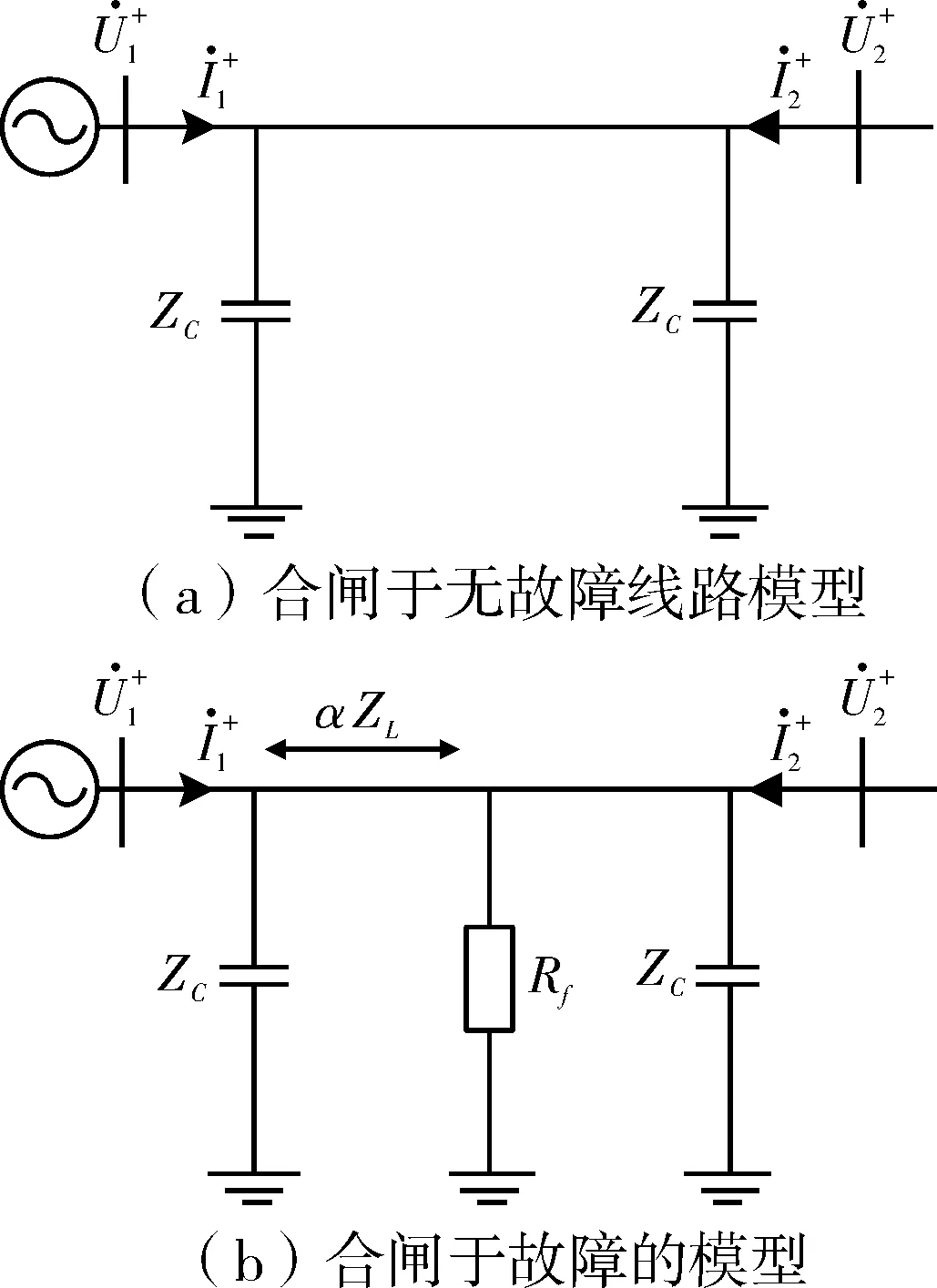
图1为含IIDG的简单配电网示意图。本文涉及的分布式电源都采用低电压穿越特性的控制策略,具体控制方式文献[11]详细给出,此处不再赘述。
定义线路两端正序电压之和与线路两端正序电流之和的比值为正序和商阻抗。
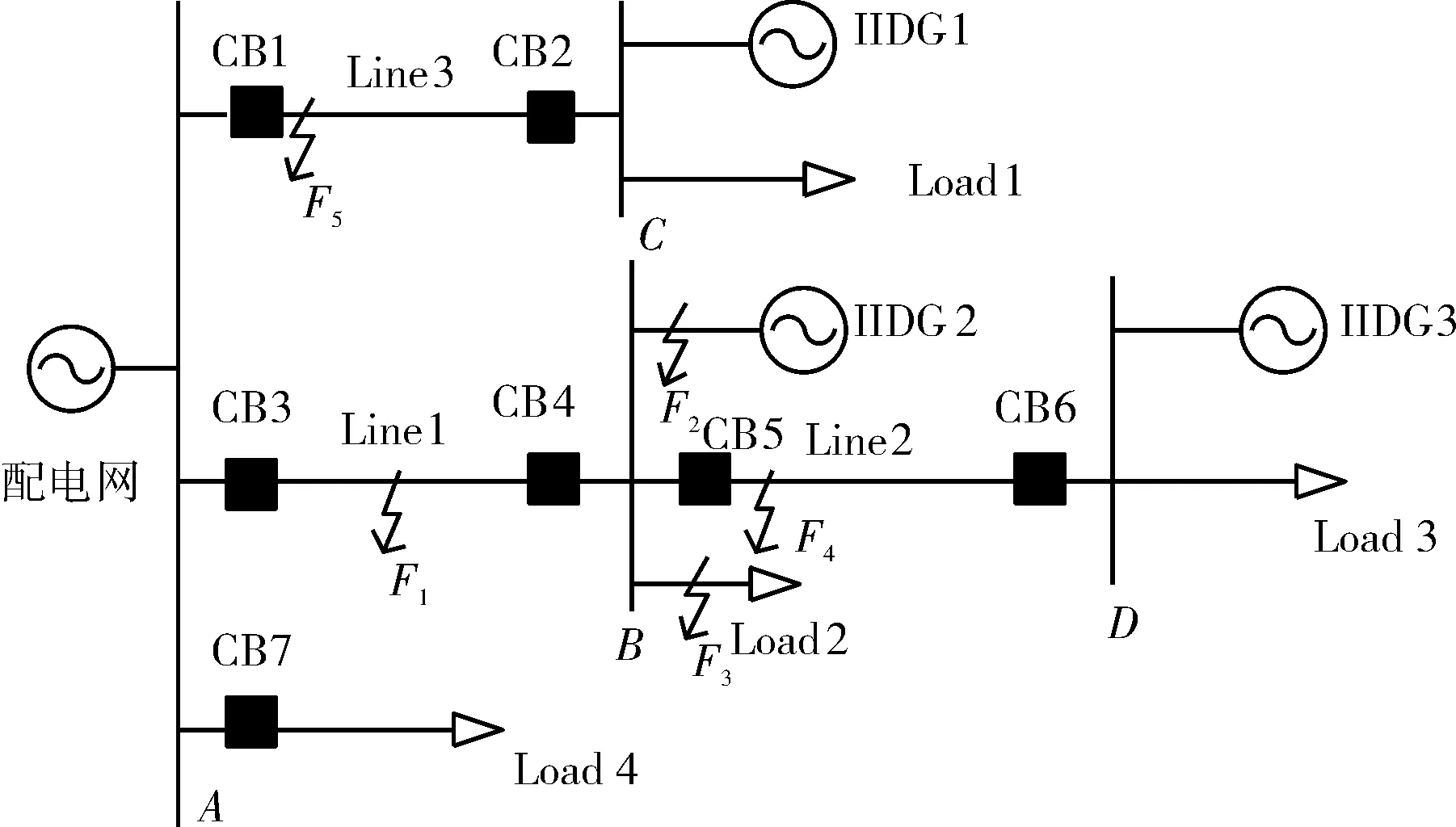
图 1 含IIDG的配电网示意图
(1)
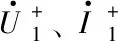
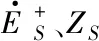
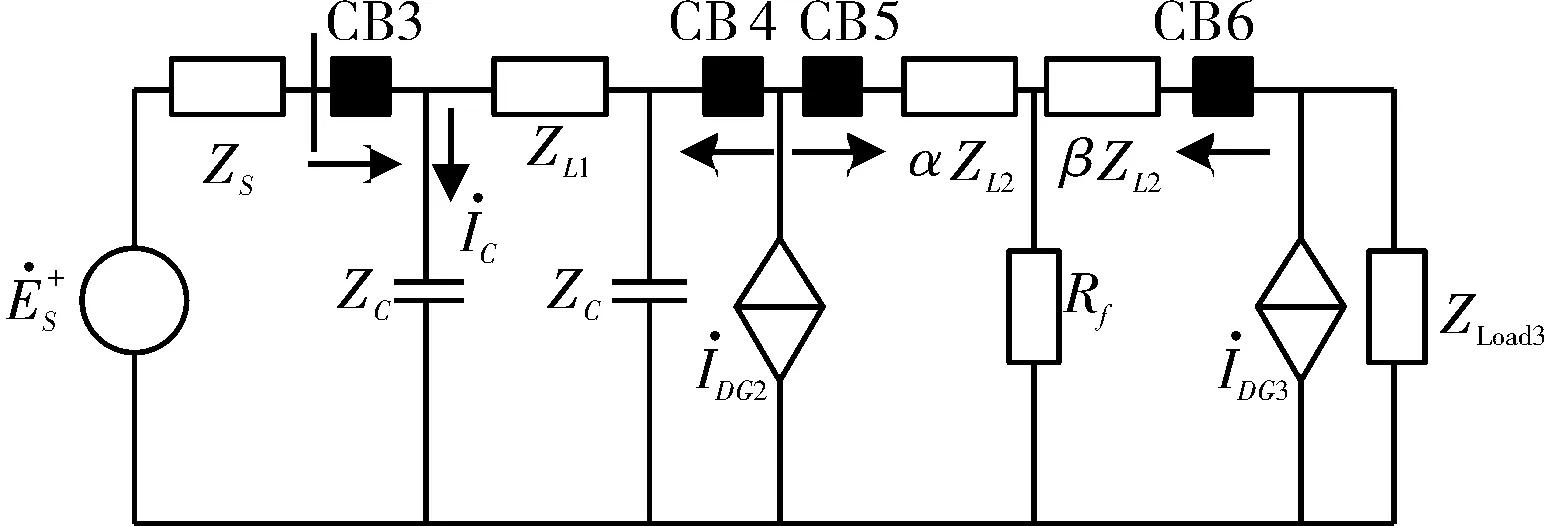
图 2 区外F4故障正序分量网络
此时有
(2)
区外故障正序和商阻抗为
Zcd=ZC
(3)
即线路发生区外故障时,Zcd为线路容抗值,相对于系统和线路的正序阻抗,其值较大。
2)区内故障。35 kV及以下配电网大多采用中性点不接地的方式运行,当系统发生相间故障时,中性点不接地系统与中性点接地系统相间短路的正序网络图相同;当系统发生相间接地故障时,电源与故障点之间无法形成回路,此时中性点不接地系统与中性点接地系统相间接地故障的正序网络图将不同:因此,有必要将相间故障与相间接地故障分开讨论。
①区内发生相间故障时,正序故障分量中包含的电容电流可以忽略。图3为线路Line1发生区内两相短路时的正序网络图。
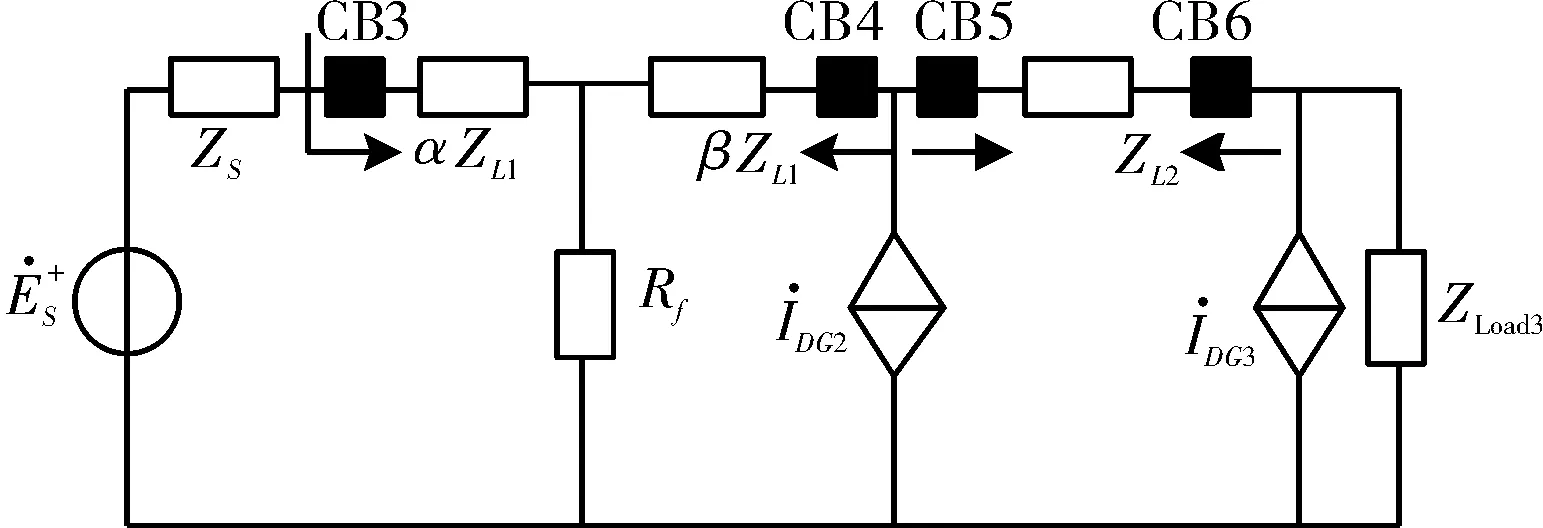
图 3 区内相间故障正序分量网络
根据图3可得馈线正序电压分别为:
(4)
(5)
(6)
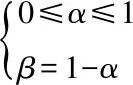
则|Zcd|满足
|Zcd|≤|ZL1+2Rf|<|ZL1|+2Rf
(7)
即线路发生区内相间故障时|Zcd|max=|ZL1|+2Rf。
②区内发生两相接地故障时,文献[13]利用对称分量法详细推导了中性点不接地系统BC相经过渡电阻接地时A相序分量关系:
(8)
式中:Ua1、Ua2、Ua0分别为A相的正序、负序和零序电压;X2∑为A相负序阻抗;Ia1为A相正序电流。输电线路的正序阻抗与负序阻抗相等,可知中性点不接地系统的正序网络中除故障支路电阻将变为原来的2倍以外,其他参数不变。
可知,区内发生相间接地故障时的正序网络图与图3相似,只是将过渡电阻支路由Rf替换为2Rf。用2Rf依次替换式(4)(5)(6)(7)中的Rf,此时|Zcd|满足
|Zcd|≤|ZL1+4Rf|<|ZL1|+4Rf
(9)
即线路发生区内相间接地故障时
|Zcd|max=|ZL1|+4Rf
(10)
参照文献[14-15],10 kV电压等级线路供电半径和线路对地电容电流有表1的特点。
1.2 基于正序和商阻抗的纵联保护判据
通过以上分析可知,当线路区内无故障时理论上测量得到的|Zcd|值为对地容抗值,|Zcd|在10 kV
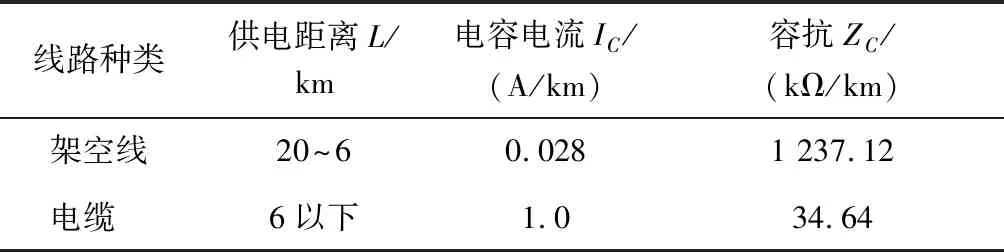
表1 不同线路类型的10 kV线路特点
供电范围内为一个kΩ级别的数值,具体数值由输电线路的电压等级、线路长度和线路种类确定。当线路发生区内故障时,相同过渡电阻条件下,将在线路发生相间接地故障时得到|Zcd|最大值,为|ZL1|+4Rf。中低压配电网相间故障Rf取值一般为1~2Ω,发生接地故障时Rf的取值可以从0到几百Ω[16];因此,可以根据|Zcd|的大小来区分是线路区内故障还是区外故障。据此提出基于正序和商阻抗的纵联保护原理,判据为
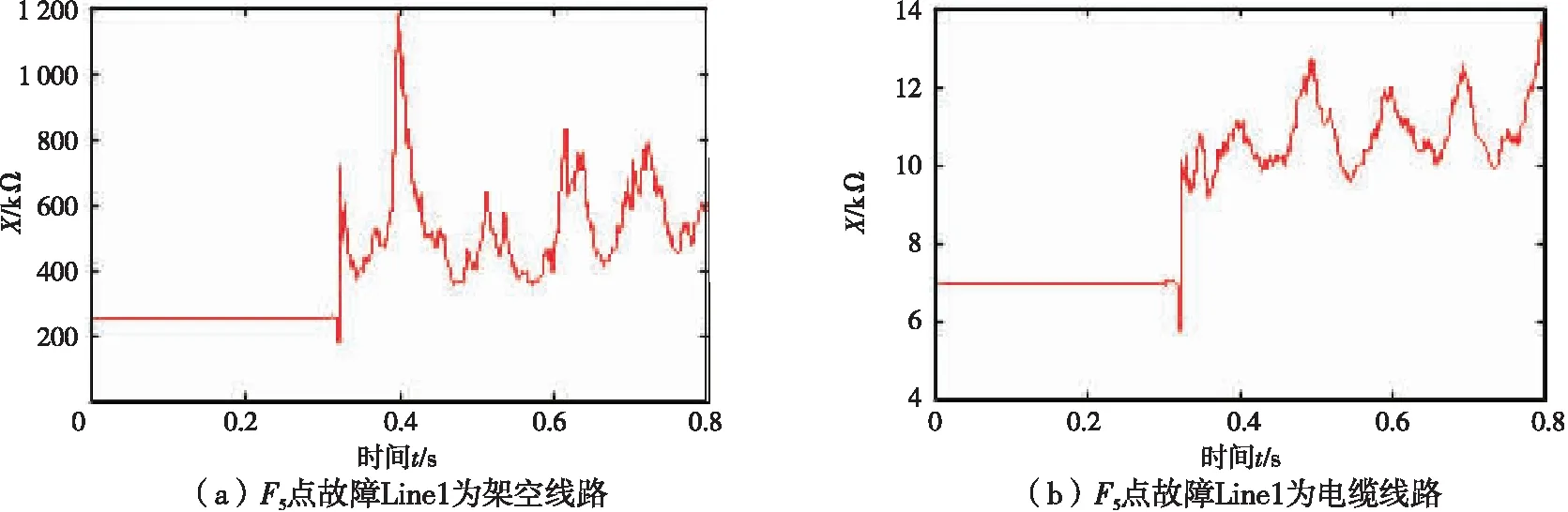
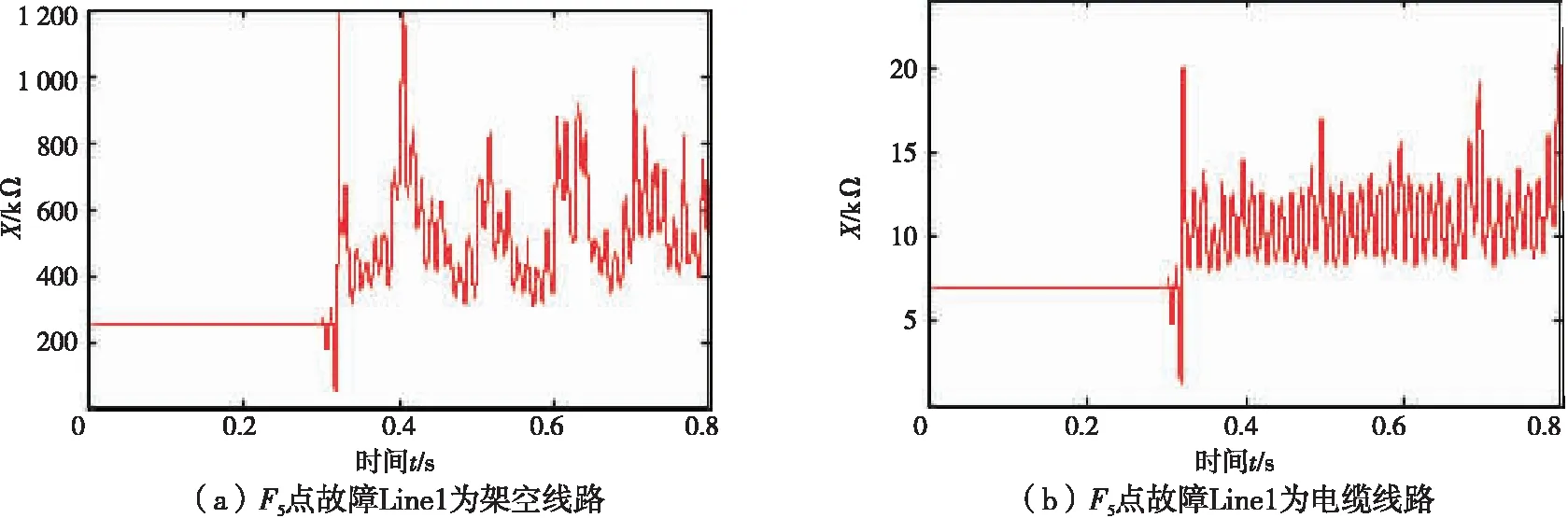
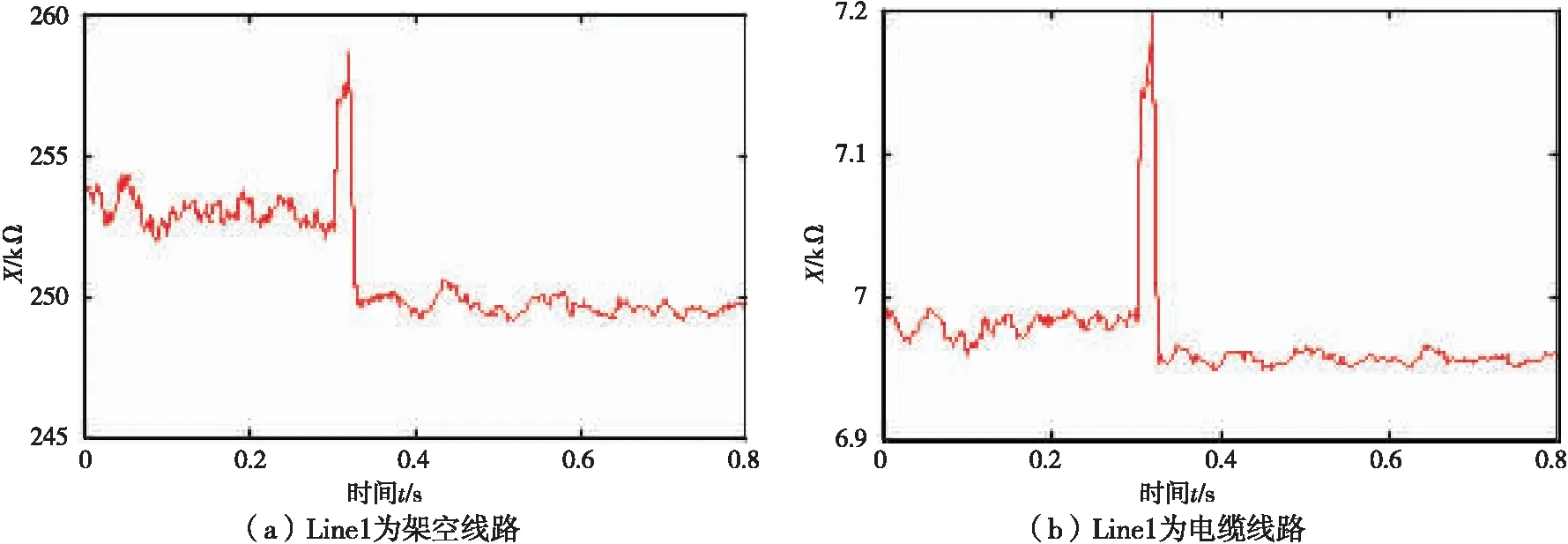
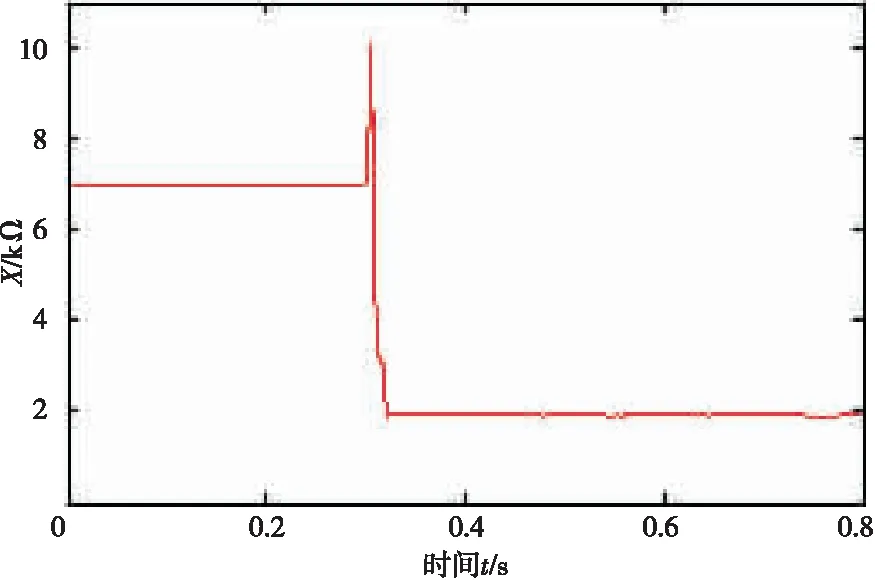
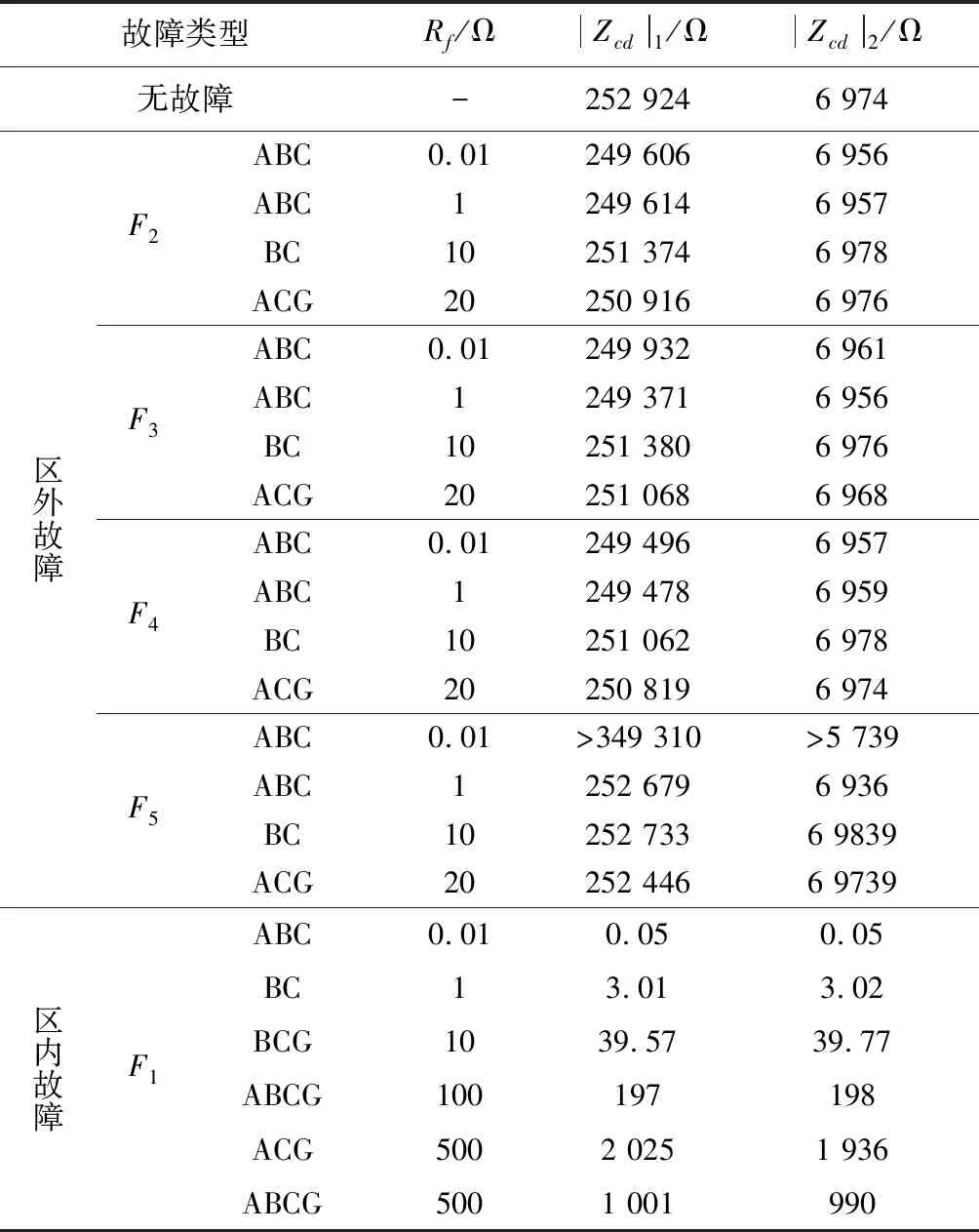
|Zcd| (11) 式中Zset为阻抗定值。整定原则为 Zset=kZC (12) 式中k为可靠系数,从第3节仿真结果可知k一般可取0.5~0.6,能够保证区外故障不误动。 以电压等级为10 kV、长度为5 km的电缆线路为例,ZC的值约为6.93 kΩ,可以将Zset整定为3.47~4.16 kΩ。当线路长度变短时,ZC值将变大,由式(12)整定的Zset也将变大,为便于整定,此时可将Zset直接取为3.47 kΩ。 基于正序和商阻抗纵联保护的输电线路,其动作值只与线路对地容抗值ZC有关。在实际的配电网当中,线路种类和长度一旦确定,ZC值主要受环境因素的影响,相较于故障状态其值变化不大。低压配电网线路容抗值远大于可能出现的过渡电阻值,因此只要式(12)中的可靠系数选取合理,即使线路区内发生大过渡电阻接地故障,也能实现故障的快速识别。 在高压输电线路的电流纵联保护中,当暂态分量超过一定值时必须退出保护,并提高动作门槛,然而电容电流较大暂态分量消失较慢,从而降低了灵敏度。对于中低压配电网系统,电容电流较小,由第3节大量仿真可知,Line1下游发生故障时,电容电流几乎不影响|Zcd|的测量值;当故障发生在Line2上游母线出口处时,受IIDG控制策略影响,|Zcd|值将发生震荡,只要可靠系数选取得当仍能避免保护误动。当线路发生区内故障时,只有故障电流值与原电压等级线路对地电容电流值接近,电容电流含有的直流分量才会明显影响|Zcd|的测量值,此时对应线路发生大过渡电阻故障,直流分量将迅速衰减。因此,线路区内发生大过渡电阻故障而受到暂态分量的影响时,保护仍会快速动作。 当系统发生故障时,IIDG的控制策略将影响其输出电流与接入点电压的相位。由于本文涉及的IIDG采用正序分量的控制策略,当线路发生不对称故障时,其输出的故障电流只包含正序分量,即IIDG只包含在正序网络中。线路区内外无故障时,分别采用电压电流全相量和正序电压电流相量计算得到的|Zcd|值将相等。线路区外一旦发生故障,电压电流全相量包含的负序分量将导致计算值|Zcd|产生较大波动,容易导致保护误动,而采用正序和商阻抗的纵联保护很好地解决了这一问题。 由于可再生能源的间歇性,难免造成分布式电源的频繁投切,而分布式电源出力发生改变及投切过程中线路对地电容不会发生改变;因此,对判据(11)中的|Zcd|计算值影响不大,本文提出的正序和商纵联保护原理在DG出力发生改变及投切过程中仍具有较好的适用性。 线路空载合闸模型如图4所示,图4(a)为合闸于无故障的线路模型,图4(b)为合闸于故障的模型。 图 4 空载合闸系统模型图 当线路无故障时,如图4(a),正序和商阻抗满足式(3),为 |Zcd|=ZC 当线路存在故障时,如图4(b),则 式中ZL为线路阻抗。可见:在线路合闸时,若线路无故障,|Zcd|与ZC相等;若线路有故障,|Zcd|反映保护安装处到故障点的线路阻抗与过渡电阻之和,其值与线路容抗值相差较大。基于此,使用基于正序和商阻抗的纵联保护判据可以区分线路上是否有故障。 为验证所提保护原理在复杂配电网中的适应性,采用PSCAD仿真软件搭建如图1所示的有源配电网模型。配电网电压等级为10 kV,容量为10 MVA, IIDG采用低电压穿越的PQ运行控制策略,IIDG1—IIDG2的额定容量为0.5 MVA。线路采用∏型等效参数模型,线路Line1、Line2长度分别为5、4 km,Load1—Load4为三相负载,视载功率分别为0.9、0.5、1、2 MVA,且功率因数都为0.9。仿真中,分别在F1—F55个点模拟不同故障,整定时k取值为0.5。 仿真模型1:Line1、Line2都为架空线路,单位阻抗和导纳分别为0.838+j0.395 Ω/km,1.545×10-8S/km。 仿真模型2:Line1为电缆线路,单位阻抗和导纳分别为 0.870+j0.120 Ω/km,5.516×10-7S/km;Line2为架空线路,单位阻抗和导纳分别为 0.838+j0.395 Ω/km,1.545×10-8S/km。 设定t=0.3 s时发生故障,此时系统电压下降将会导致IIDG的出力发生改变,从而对正序和商阻抗的计算产生影响。图5与图6表示母线A出口F5处发生三相金属性短路时,线路Line1为不同线路种类,分别采用电压电流正序分量和全相量得到的|Zcd|测量值。 从图5可以看出,当系统发生严重故障时,由于IIDG失去了系统电压的支撑,IIDG将进行低电压穿越,因此在故障发生一个周期内|Zcd|发生较大的震荡,随后测量值超过稳态值并继续震荡。图5(a)和图5(b)中的最小值分别为349.31 kΩ和5.739 kΩ,都能满足保护不误动。 图6为采用电压电流全相量计算得到的|Zcd|值。与图5对比可知:系统无故障时,2种方法计算得到的|Zcd|值相等;区外发生故障时,一个周期内|Zcd|也会发生震荡,但是采用全向量计算得到|Zcd|的震荡幅度远大于采用正序分量计算得到|Zcd|的震荡幅度,容易导致保护的误动作。仿真验证了采用正序分量和商阻抗保护的稳定性。 图 5 采用正序分量|Zcd|的测量值 图 6 采用全相量时|Zcd|的测量值 图7表示在F4点发生三相金属性短路时,Line1为不同线路种类时|Zcd|的测量值。与图5所示情况不同,虽然系统电压也会有所下降,但Line1靠近系统侧,受分布式电源出力影响较小,|Zcd|值震荡较小,因此在较短时间内|Zcd|值接近稳定值。 图 7 F4点故障时|Zcd|的测量值 表2列出了当Line1为电缆线路时,在系统不同位置发生故障时|Zcd|的稳态测量值。从表2可以看出,当线路发生区内大过渡电阻接地故障时,故障线路|Zcd|的测量值与第1节理论分析符合,基本接近2Rf或4Rf,|Zcd|值相对于ZC较小,最大值为2 025 Ω。当区外发生故障时,其数值大于5 kΩ。可见,使用判据式(11)可以很容易地区分线路区内、区外故障,因此基于正序和商阻抗的纵联保护原理可以应用于含IIDG的配电网线路。 图 8 F2点故障时|Zcd|的测量值 故障类型Rf/ΩZcd1/ΩZcd2/Ω无故障-252 9246 974区外故障F2F3F4F5ABCABCBCACGABCABCBCACGABCABCBCACGABCABCBCACG0.01110200.01110200.01110200.0111020249 606249 614251 374250 916249 932249 371251 380251 068249 496249 478251 062250 819>349 310252 679252 733252 4466 9566 9576 9786 9766 9616 9566 9766 9686 9576 9596 9786 974>5 7396 9366 98396 9739区内故障F1ABCBCBCGABCGACGABCG0.011101005005000.053.0139.571972 0251 0010.053.0239.771981 936990 注:|Zcd|1、|Zcd|2分别为模型1和模型2中|Zcd|的测量值 本文提出一种基于正序和商阻抗的纵联保护新原理,并进行了理论分析和PSCAD/EMTDC仿真验证。理论分析和仿真结果表明:区外发生故障时,新原理的动作量反映线路容抗,其数量级为kΩ;区内发生故障时,忽略线路电阻时动作量反映2倍或4倍的过渡电阻值,二者数值差别较大,保证了基于正序和商阻抗的纵联保护的灵敏性。该原理适用于含IIDG的配电网保护,具有容易整定、动作灵敏、抗过渡电阻能力强的优点。仿真结果验证了新原理的有效性。2 正序和商阻抗算法的性能分析
2.1 耐受过渡电阻能力分析
2.2 受暂态分量的影响分析
2.3 受IIDG控制策略的影响分析
2.4 DG出力干扰分析
2.5 空载合闸分析
3 仿真验证
3.1 仿真结构及参数
3.2 仿真结果
4 结论

