UHPC薄板屈曲试验及临界板厚比研究
吴延伟
(中铁第一勘察设计院集团有限公司,西安 710043)
1 概述
超高性能混凝土UHPC(Ultra-high Performance Concrete)是一种具有高强度力学性能的混凝土材料,该材料在铁路桥梁工程中主要应用于人行道板、道砟槽板等,桥梁主体受力结构采用UHPC材料建造的工程实例较少,该材料应用的深度和广度有待提高。
为了促进UHPC在桥梁主体受力结构的应用,国内外学者进行了一系列的理论研究和试验研究。张哲[1]等开展了超高性能混凝土轴拉性能试验研究,研究表明钢纤维的形状和掺量是影响UHPC材料初裂应变的关键因素等。曹霞[2]等开展了不同纵筋率高强钢筋RPC梁抗剪承载力及剪切延性试验研究,研究表明高强钢筋RPC梁正常使用极限状态下最大裂缝宽度不超过0.3 mm、梁截面应变符合平截面假定、并拟合出高强钢筋超高性能混凝土梁抗剪承载力经验公式等;孙明德[3-4]等开展了高强钢筋活性粉末混凝土梁抗弯性能试验研究和高强钢筋与活性粉末混凝土粘结性能试验研究,研究表明RPC适筋梁正截面破坏过程与普通混凝土梁相似、提出钢筋与RPC之间的粘结长度和最小保护层要求等。刘琛[5]研究了铁路大跨度活性粉末混凝土简支梁截面形式,提出活性粉末混凝土和普通混凝土组合结构截面,并指出RPC梁多为细长柱结构,设计阶段应进行稳定性分析。李志光[6]、金凌志[7]、徐海宾等[8-16]还进行了活性粉末混凝土桥梁其他关键技术问题的研究。总之,针对UHPC结构的轴拉、抗弯、抗剪等试验研究已取得一定的研究成果,而UHPC桥梁屈曲问题仍停留在理论计算阶段,屈曲试验研究较为欠缺。
与普通混凝土相比,UHPC材料更优,构件尺寸设计可以更加纤细[17]。因此,UHPC作为高强度的力学材料,在铁路简支箱梁设计时必然采用薄壁形结构,UHPC桥梁设计不仅需要考虑结构的整体稳定,还需考虑组成箱形截面的悬臂板、腹板间顶板和腹板的局部失稳问题[18]。本文通过19个UHPC薄板试件屈曲试验,研究其局部失稳破坏特征,提出UHPC薄板屈曲承载力影响因素及不同边界条件下UHPC板的临界板厚比。
2 UHPC薄板试验
2.1 试验构件及试验板制作
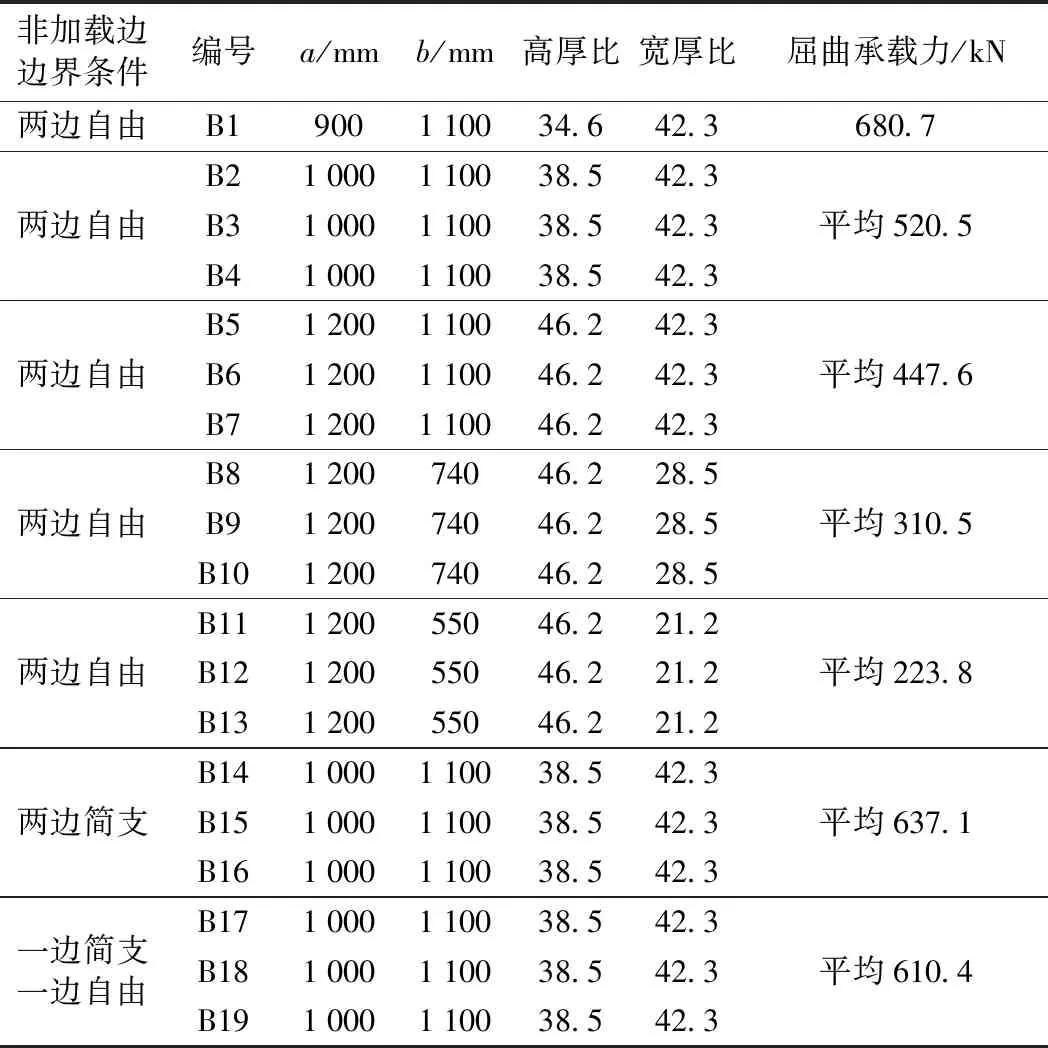
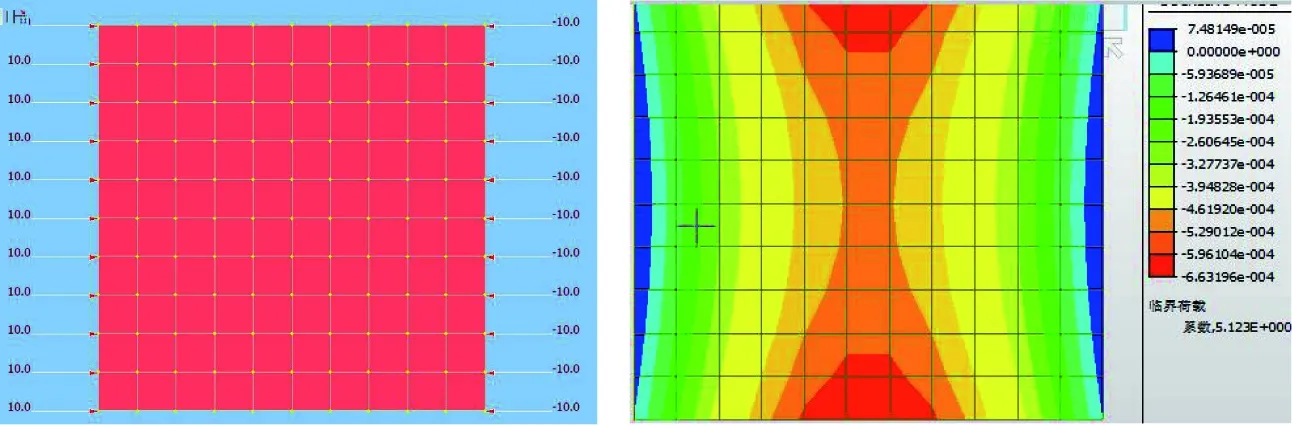
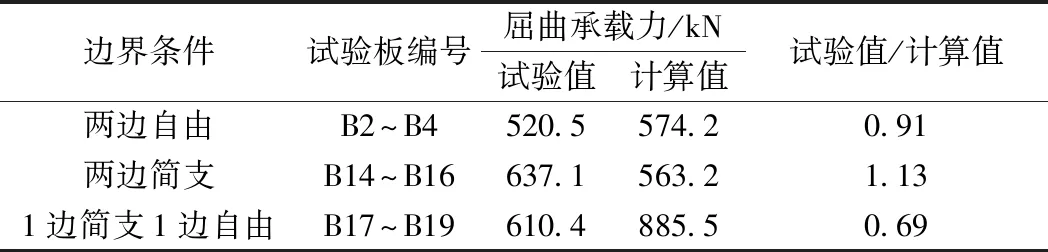
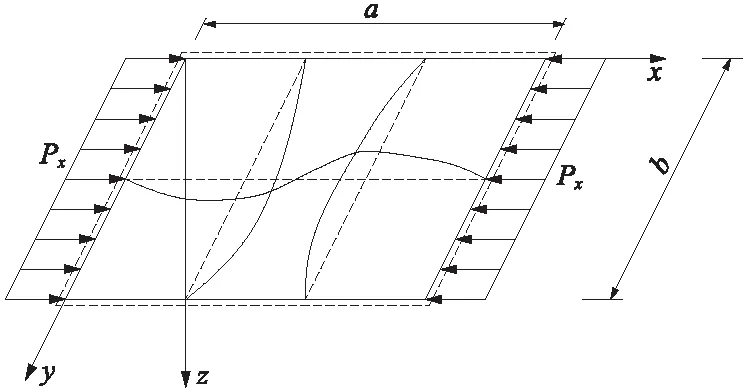
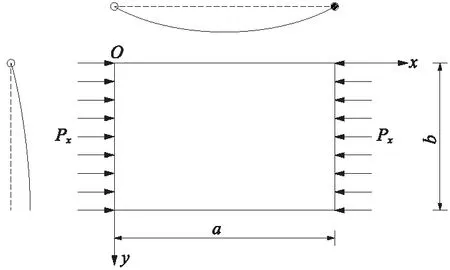
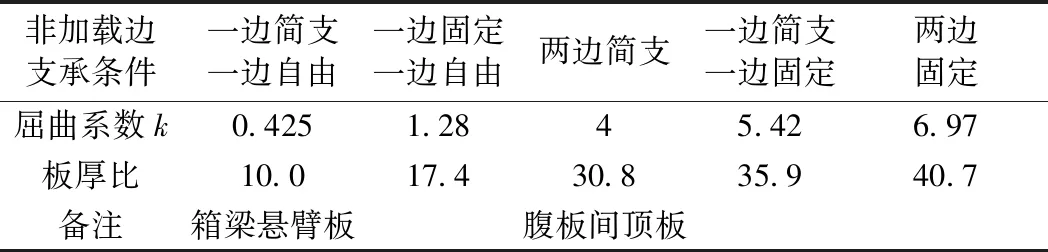
板按照其厚度可分为厚板、薄板和薄膜3种。将板的厚度t与板幅面的最小宽度b相比,当(1∶80~1∶100) UHPC试验板均为矩形薄板,板的高厚比、宽厚比和边界条件为主要变化参数,板的厚度均为26 mm,高厚比30.8~46.2,宽厚比21.2~42.3,共19个试件,边界条件为四边简支、两边简支两边自由、两边固定两边自由。试件制作配合比见表1,试验板的UHPC立方体强度为120 MPa,弹模为46 GPa。养护制度为40 ℃蒸汽养护24 h后拆模,再进行75 ℃蒸汽养护48 h,静置7 d后进行加载试验。 表1 UHPC薄板试件配合比 UHPC矩形板的加载方案见图1,当板的侧边无约束时,沿着板的竖轴中心线上均匀布置5个位移计,见图2;其他边界条件时,在板中心、横轴中心线和竖轴中心线布置5个位移计,呈十字形,见图2。试验参照GB/T 50152—2012《混凝土结构试验方法标准》进行,数据采集采用DH3816静态应变仪,记录每级荷载下的水平位移和UHPC板的破坏情况。 图1 UHPC板加载示意 图2 位移计测点布置 板的破坏形态有3种:一是板顶端或者底部局部受压破坏,如图3(a);二是板的单方向裂缝行为,当板的宽度较窄时,在板的竖向产生3条横向裂缝,如图3(b),板较宽时,在板的中间产生1条裂缝,如图3(c);三是双向裂缝行为,板在竖向和横向产生了双向曲率裂缝破坏模式,裂缝都是完全对称的,如图3(d)和图3(e);单方向行为和双向行为的板都是突然破坏,脆性断裂,且在断裂时产生爆炸式巨响。屈曲试验结果见表2。 从表2可知:①屈曲承载力随高厚比的增加而减小,当高厚比由38.5变化到46.2时,屈曲承载力降低了16.3%;②屈曲承载力随着宽厚比的增大而增大;③不同边界条件试验表明:在高厚比、宽厚比相同时,非加载边两边自由、一边简支一边自由和两边简支时的屈曲承载力为P两边自由 图3 UHPC薄板破坏形式 非加载边边界条件两边自由两边自由两边自由两边自由两边自由两边简支一边简支一边自由编号a/mmb/mm高厚比宽厚比B1900110034.642.3B21000110038.542.3B31000110038.542.3B41000110038.542.3B51200110046.242.3B61200110046.242.3B71200110046.242.3B8120074046.228.5B9120074046.228.5B10120074046.228.5B11120055046.221.2B12120055046.221.2B13120055046.221.2B141000110038.542.3B151000110038.542.3B161000110038.542.3B171000110038.542.3B181000110038.542.3B191000110038.542.3屈曲承载力/kN680.7平均520.5平均447.6平均310.5平均223.8平均637.1平均610.4 利用MIDAS软件建立UHPC矩形板的有限元模型,以B15板为例,施加荷载110 kN,程序计算局部失稳荷载系数为5.12,即B15板的理论计算屈曲荷载为563.2 kN,见图4。试验板理论计算与试验数据对比见表3,由表3可知:试验值与计算值比值为0.69~1.13,考虑到UHPC材料均一性及制作初始缺陷等因素的影响,试验值与计算值基本吻合。偏于安全起见,UHPC板屈曲承载力计算时应取折减系数0.7。 图4 有限元计算模型及结果(试件编号B15) 边界条件试验板编号屈曲承载力/kN试验值计算值试验值/计算值两边自由B2~B4520.5574.20.91两边简支B14~B16637.1563.21.131边简支1边自由B17~B19610.4885.50.69 沿UHPC试验板的垂直中心线的荷载-法向位移曲线见图5。其中B7板边界条件为两边自由,B16板边界条件为两边简支。根据试验测试结果,试件在加载初期变形不明显,随着荷载增加,由于加载的初始偏心和试验板浇筑制作时的初始缺陷,UHPC板在一个方向产生弯曲变形,随着荷载的增加,产生的法向位移逐渐增大,继续加载直到板发生破坏,法向位移的最大幅值大多出现在板的1/2高度位置。 图5 竖向垂直线的横向变形 屈曲承载力的判断准则:在荷载作用下板的平衡状态开始丧失稳定,稍有扰动则变形迅速增大,最后结构破坏。板在同级荷载加载下,法向变形增大的幅度很大时的荷载即为屈曲承载力,如图B7板的屈曲荷载为422 kN,B16板的屈曲荷载为620 kN。所有UHPC板只在一个方向产生变形,即只产生一个半波。B5~B7板实测平均屈曲承载力为447.6 kN,B14~B16板实测平均屈曲承载力为637.1 kN。 铁路UHPC桥梁一般采用箱形截面[5],箱梁底板和腹板一般布置有预应力钢束,底板和腹板因钢束波纹管对于构造的控制而板厚比较小,且底板和腹板的压应力水平通常较低,因此难以发生局部失稳。 UHPC箱梁的顶板通常承受较大的压应力且板厚较大,易发生局部失稳破坏。箱梁的腹板间顶板计算模型为两边简支板,见图6。箱梁的悬臂板计算模型为一边简支一边自由板,见图7。 图6 单向均匀受压两边简支板 图7 均匀受压一边简支一边自由板 当局部失稳状态下的欧拉应力σcr大于材料屈服应力fy,则理论上受压板件弹性稳定不控制设计,结构强度破坏早于失稳破坏。对于混凝土和钢构件,一般要求弹性稳定安全系数不小于4[20],按照一般混凝土构件允许应力约为混凝土轴心抗压强度的0.5倍考虑,即欧拉应力σcr大于UHPC轴心抗压强度的2倍时,板件局部失稳不控制设计。对于本试验120 MPa级UHPC材料,其轴心抗压强度由试验得出为87.6 MPa[21],其屈曲失稳欧拉应力σcr为175.2 MPa。屈曲失稳欧拉应力σcr计算公式如下[22] 式中,k为屈曲系数,根据非加载边的支承条件类型取值见表4;E为UHPC的弹性模量,试验实测值为46 GPa;泊松比ν为0.3;b和t分别为板的宽度和厚度。 将欧拉应力175.2 MPa代入公式,计算不同边界条件下的板厚比见表4。 表4 加载边简支时单项均匀受压板的屈曲系数 (1)UHPC薄板的屈曲形态主要有3种:①板顶端或者底部局部受压破坏;②板的单方向裂缝行为,板较窄时,在板的竖向产生3条横向裂缝,板较宽时,在板的中间产生1条裂缝;③双向裂缝行为,板在竖向和横向产生了双向曲率裂缝破坏模式,裂缝都是完全对称的。 (2)屈曲荷载试验值和理论计算值的误差在0.69~1.13,两值基本吻合。考虑到UHPC材料、制作等因素的影响,UHPC板屈曲承载力计算时应取折减系数0.7。 (3)UHPC板法向位移的最大幅值大多出现在板的1/2高度位置,本试验UHPC所有板件只在一个方向产生变形,即只产生一个半波。 (4)UHPC板屈曲荷载及失稳时临界应力可根据欧拉公式计算,欧拉应力可为UHPC轴心抗压强度实测值的2倍,由此推导板的临界板厚比。箱梁腹板间顶板最小板厚比为30.8,箱梁悬臂板的最小板厚比为10.0,最小板厚比不足时应增加UHPC板厚度或采取加劲措施满足稳定性要求,避免失稳破坏先于强度破坏。
2.2 试验装置及测试方案
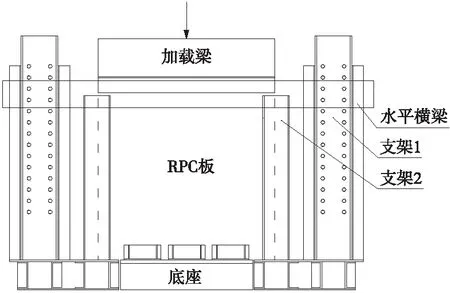
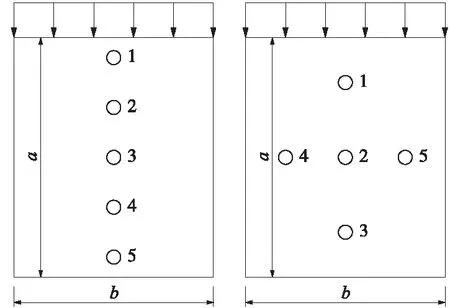
3 试验结果与分析
3.1 UHPC板的破坏形态及屈曲荷载

3.2 屈曲荷载计算
3.3 UHPC板屈曲荷载变形曲线
4 临界板厚比
5 结论

