截断混合高斯分布入组模式下生存资料样本量估计*
胡海霞 王 陵 李 晨 李 凡 朱 典 康其传 李婵娟 夏结来△
【提 要】 目的 在入组间期长的生存资料临床试验中,受试者入组速率可能受招募广告宣传等多因素影响而存在反复波动,本文采用截断混合高斯分布拟合这种入组速率变化并估计该入组模式下需要的样本量。方法 在指数分布生存时间和指数失访假设下,采用多重积分法推导受试者入组速率服从截断混合高斯分布时的事件发生率及样本量计算公式;分别计算截断混合高斯分布中均值、方差、权重分配变化时样本量变化情况;通过Monte Carlo模拟对采用均匀分布估计波动入组速率可能引起的试验检验效能损失及对提出样本量计算公式的稳健性进行评价。结果 截断混合高斯入组模式下各高斯组分的均值越小、均值较小高斯组分的方差越小、权重越大,需要的样本量越小,即受试者入组速率高峰出现较晚或早期入组速率波峰窄小时需要更多的样本量;采用均匀分布拟合波动入组速率可能会引起不同程度的试验检验效能不足,而在截断混合高斯入组模式计算的样本量下试验检验效能基本能稳定在预期水平;截断混合高斯入组模式还可以近似恒定入组速率,单调增或减入组速率等情况。结论 截断混合高斯入组模式及提出的样本量计算公式具有较好的稳健性,适用性更广,可以用于生存资料临床试验样本量估计。
生存资料临床试验设计时,需要对受试者入组速率、生存时间分布、失访等进行合理假设或估计。目前在估计试验需要的样本量时,多假设入组间期内受试者入组速率恒定,即均匀入组[1-3]。为避免受试者入组速率比预计慢,受试者集中在入组间期后期入组,平均随访时间不足引起试验检验效能不足,Lachin等人[4]提出了截断指数分布入组模式,通过调整截断指数分布的参数近似不同的受试者入组速率变化。在多中心临床试验中,各个分中心开始招募受试者时间不统一,受试者入组速率可能会因各试验中心的陆续启动呈现阶梯上升,因此有学者提出分段常数入组模式[5-8]。为了拟合实践过程中可能出现的多种入组速率改变,Yateman[9]提出了分段线性入组模式,将入组间期分割为若干小间隔,分间隔分别描述受试者入组速率。Maki[10]将截断指数分布作为分段分布内的某一段分布使得分段入组模式更灵活。此外,线性递增和线性递减分布[2]也被用于受试者入组速率估计。在同质和非同质泊松分布入组模式[11-12]下,有学者提出运用贝叶斯理论预测入组速率分布,但理论相对复杂,尚未被广泛应用。
临床实践中受试者入组可能受多个因素影响,因而入组速率可能会出现波动变化,如试验启动时,由于前期累积受试者的存在,入组速率呈现递增趋势,随着目标受试者的消耗,入组速率降低。Gesualdo[13]等人的研究发现视频宣传能有效促进受试者入组,因此在入组间期长,需要受试者多的大型临床试验中,由于招募受试者受广告宣传的影响,入组速率可能呈现紧随广告效应变化的波动趋势。针对这一可能的情形,目前存在的入组速率模型均不能很好的进行拟合。
混合高斯分布(Gaussian mixture distribution,GMD)是由多个独立高斯分布加权获得的混合函数,可以对各种形状的密度函数曲线进行光滑拟合,现已被广泛应用于信号处理[14]和医学遗传领域[15]。其波浪形的密度曲线形状与多因素影响下(如受广告效应影响)的入组速率变化情形类似,因此本文拟利用这一特性,采用截断后的混合高斯分布对波动的受试者入组速率进行拟合,在此基础上推导指数分布生存时间和指数失访假设下该入组模式需要的样本量估计公式。
模型构建及样本量计算公式
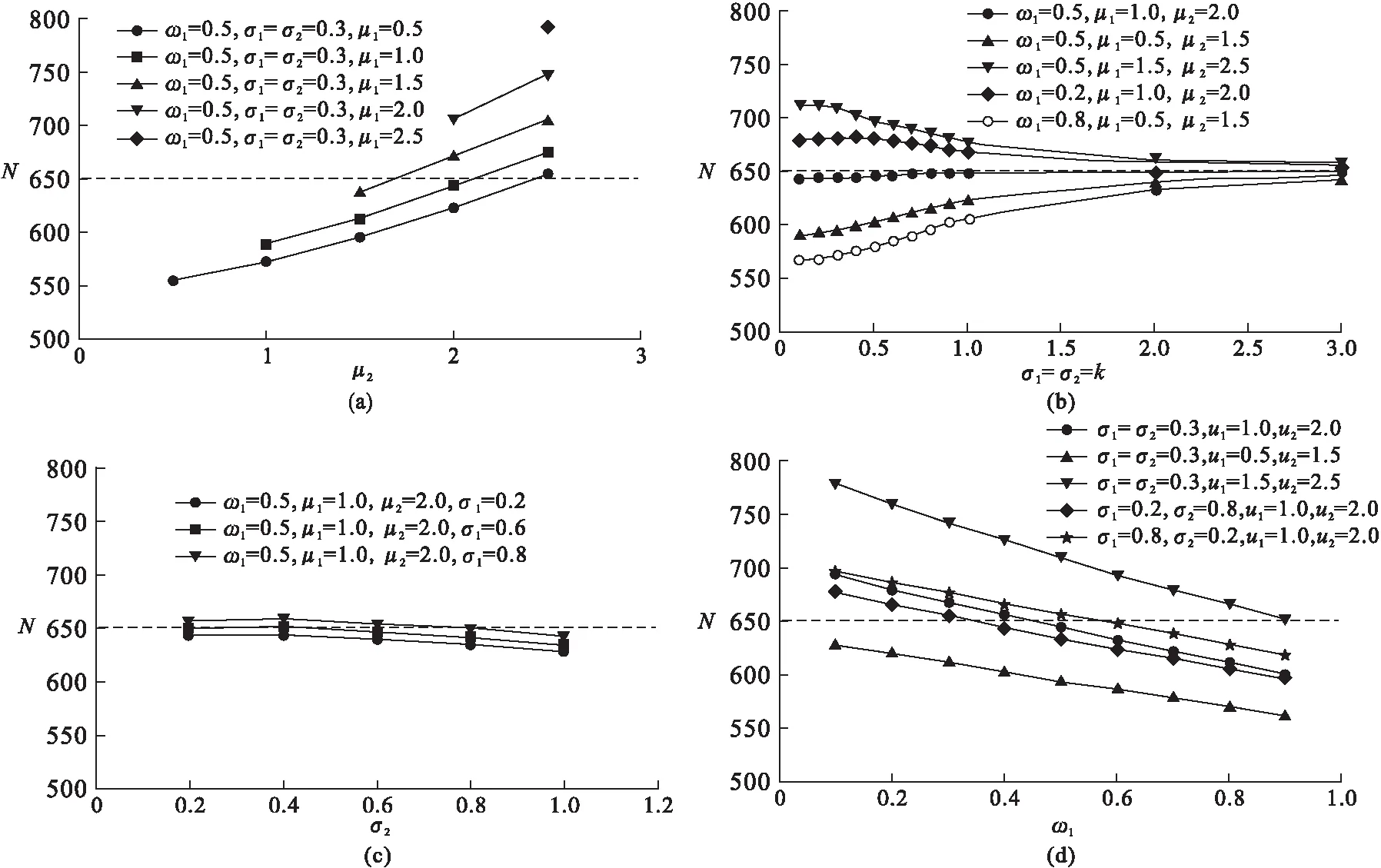
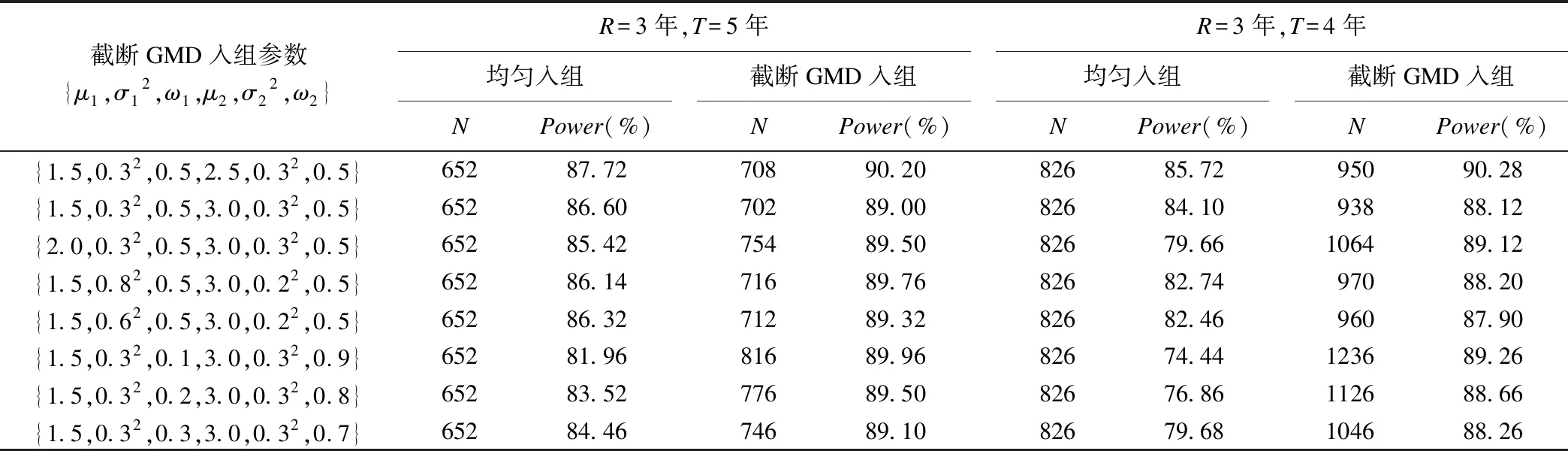
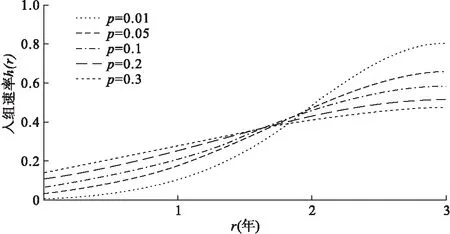
假定一个双臂随机对照生存试验,受试者1∶1随机分配到试验组和对照组。rij为第i组(i=1表示试验组,i=2表示对照组)第j个(j=1,2,…N/2,N为试验总人数)受试者入组时间(0 受试者若在试验期间失访,则无法观察到其兴趣事件(死亡),故当受试者均匀入组,即入组时间分布服从概率密度函数g(r)=1/R时,第i组受试者死亡的概率为在随访期间内可能发生失访的时间点前发生兴趣事件的累积概率,公式表示如下: (1) 其中,δ为死亡指示变量,δij=1表示第i组的第j个受试者在试验随访期间死亡,δij=0表示没有死亡;τ为最长随访时间,τij=T-rij,(T-R≤τij≤T)。同理,第i组失访受试者的比例表示为: 其中,ξ为失访指示变量,ξij=1表示第i组的第j个受试者在试验随访期间失访,ξij=0表示没有失访;根据预先估计的失访比例迭代计算(2)式可获得两组受试者失访时间的指数分布参数ηi。 当受试者入组速率不恒定并且有波动时,如受招募广告宣传及目标受试者消耗等影响时入组速率表现为多峰分布,此时可以采用GMD进行拟合,GMD表达式如下: (3) (4) (5) (6) 为探讨截断混合高斯分布中各高斯组分的均值、方差、权重对该入组模式下样本量的影响,为试验设计时入组速率模型参数设定提供直观的依据,我们以两组分截断GMD为例(参数Θ={μ1,σ12,ω1,μ2,σ22,ω2},μ1<μ2),计算并比较设定背景下改变不同参数值时需要的样本量N。假定一个入组间期为3年,总研究时长为5年的双臂随机对照生存试验,试验组中位生存时间为3.5年,试验组和对照组死亡风险比为0.7,两组均有10%的随机指数失访,在双侧α=0.05,1-β=0.9时按照公式(6)分别计算:(1) 两高斯组分均值变化;(2) 两高斯组分方差相等时方差值变化;(3) 两高斯组分方差不等时方差值变化;(4) 两高斯组分权重分配变化,而其他参数固定不变时样本量N的变化情况,结果见图1。根据Lachin和Foulkes[4]提出的样本量计算公式,上述背景下受试者均匀入组时需要的样本量为652,为便于对比,将均匀入组样本量作为对照标注在图中。 图1 不同截断GMD入组参数设置下样本量变化情况 由图1(a)可以看出,两高斯组分方差相等、权重平均分配时,样本量随截断GMD各高斯组分均值的增大而增大;此时若两高斯组分均值和为R(μ1+μ2=R),即两组分在入组间期内对称分布时,截断GMD入组与均匀入组需要的样本量接近;若两高斯组分均值和小于R(μ1+μ2 在广告宣传影响受试者入组速率的背景下,截断GMD各高斯组分均值表示入组速率达到最大的时间点,权重和方差表示广告宣传对持续入组的影响,即单个高斯组分入组速率波动峰越宽,方差越大,波动峰越高大,权重越大。各高斯组分均值越小,均值较小高斯组分的权重越大、方差越小,表示越多的受试者在早期进入试验,受试者平均随访时间较长,因此需要较少的样本量即能达到期望的检验效能。即广告宣传越早,持续强度越大,需要的样本量越小,这与实际经验一致。在实践中,试验设计者可根据受试者入组速率可能出现的波动峰个数、各入组速率峰值出现的大约时点及各波动峰的大小选择合适的截断混合高斯参数。在预计入组速率波动情况下,截断GMD参数设置相对灵活,如一定程度上,增大方差和增大权重会产生相同的效果,故操作者不必拘泥于参数的绝对准确。设计阶段,可以多设置一些参数进行敏感性分析,以寻求最合适的样本量。但需要注意,由于目标研究对象数量的限制,广告宣传对入组的影响是有限的,即受试者入组速率不会随着广告宣传的强度持续增大,试验设计者应该理性评估这种影响并设置合理的截断GMD参数以获得较科学的样本量估计。 生存资料临床试验设计时常假设受试者以恒定速率进入试验,即均匀入组。在这部分我们通过Monte Carlo模拟探讨受试者入组速率存在不同形式波动,尤其是入组波动峰集中在入组后期时,在均匀入组假设估计的样本量下试验的检验效能。同时,用截断GMD入组模型对波动入组速率进行拟合,并根据公式(6)计算需要的样本量,产生相应数量的随机数进行模拟研究以评价该计算方法的表现。所有模拟均采用SAS 9.2统计分析软件完成,模拟次数均为5000次,结果如表1所示。试验设计参数见注释。 如表1所示,在均匀入组假设下,当受试者入组速率出现波动,尤其是波动幅度较大,入组速率高峰出现较晚、持续强度较小时,试验检验效能均会出现不同程度的降低,且当试验随访间期较短时,检验效能降低更为明显。而采用本文提出的截断GMD入组模式估计受试者入组速率存在波动的样本量时,在各种情形下试验检验效能基本在88%以上,能达到预期水平,表现较为稳定。 表1 不同样本量估计方法下波动入组速率对试验检验效能的影响 *:试验组中位生存期为3.5年,风险比为0.7,α=0.05(双侧),1-β=0.9,两组均有10%指数失访。 混合高斯分布的密度曲线在不同参数下可以表现为多种形状,其灵活性为其拟合各种入组模式下受试者入组速率提供了可能。在均匀入组模式下,受试者入组速率近似为常数。根据上文得出的结论,随着各高斯组分方差的增大,截断GMD入组模式下需要的样本量与均匀入组需要的样本量越来越接近,因为此时在入组间期(0,R]内截断GMD的形状近似为均匀分布。令截断混合高斯分布h(r)高斯组分个数为1,均值为R/2,当h(0)/h(R/2)≥99%时在(0,R]内截断GMD分布可视为均匀分布,经推导得σ≥3.5R。即当截断GMD参数设置为{μ=0.5R,σ>3.5R,ω=1.0}时在(0,R]内可以用来拟合均匀入组速率。例如,在总研究时长T=5年的双臂随机对照生存资料临床试验中,试验组中位生存期为3.5年,试验组和对照组死亡风险比为0.7,两组各有10%指数失访,在双侧α=0.05检验水准下,欲获得90%的检验效能,在不同的入组间期长度时均匀入组和采用{μ=0.5R,σ>3.5R,ω=1.0}参数设置的截断GMD入组需要的样本量均相等(表2)。 表2 拟合恒定入组速率的截断GMD入组和均匀入组需要的样本量比较 图2 截断GMD入组拟合不同变化强度的单调增入组速率(p=h(0)/h(3)) 在固定入组间期和试验总时长的生存资料临床试验设计中,受试者入组速率估计是样本量估计的重要影响因素,目前已有多种入组速率模型相继被提出,但均存在不同程度的局限性。均匀入组假设受试者入组速率在整个入组间期内恒定,这在临床试验中是很难实现的,而入组速率比预计慢会造成试验的检验效能不足,甚至在规定入组间期内不能完成入组,试验必须被延长[16]。单调增或减入组速率假设忽略了速率的波动性,限制了其应用。在入组间期较长的临床试验中,受试者入组速率受多个因素影响,如受试者招募广告宣传,目标受试者总数的消耗和积累,疾病发病率的季节性变化等,入组速率多呈现为波动变化。如Coronary Drug Project试验[16]中,为在既定间期内完成受试者招募,采用了广播、广告、报纸宣传等手段,最终受试者入组速率呈现为多峰波浪形变化。因此在样本量大,入组间期长的大型临床试验中,受试者入组速率波动并不罕见,为了对这种入组速率进行较好的拟合及对该入组模式下需要的样本量进行更准确的估计,本文提出了截断GMD入组模式并推导了指数分布生存时间和指数失访时截断GMD入组模式下需要的样本量计算公式。 截断GMD入组模式下,当各高斯组分均值较小,早期高斯组分所占权重较大,方差较小时,需要的样本量较小。忽略受试者入组速率的波动,简单按照均匀入组计算样本量可能会造成试验检验效能不同程度的损失,且这种损失对随访时间短的试验尤其明显。因此试验设计时需要对欲采取的宣传策略、各试验中心启动时间、受试者数量进行评估,从而对受试者最大入组速率时间点及入组速率的波动情况进行预估,对试验需要的样本量进行较准确的估计。 截断GMD入组模型除可以对波动的入组速率进行描述外,还可以拟合入组速率恒定的情形和单调增或减的入组速率,因此可以作为均匀入组模型、截断指数入组模型,线性增或减入组模型的替代模型,用一种模型实现多种入组速率模式的拟合。但当截断GMD含有多个高斯组分时,由于参数较多,需要综合考虑各种因素对入组速率的影响,按照预估的入组速率变化情况进行合适的参数设置。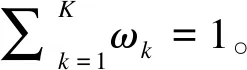

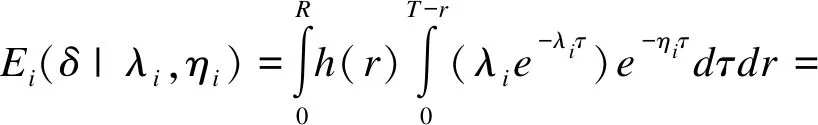

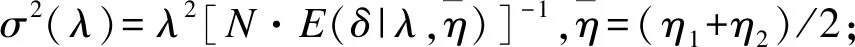
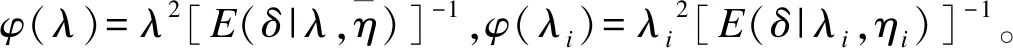
截断混合高斯分布参数对样本量的影响
波动入组速率对试验检验效能的影响
截断GMD入组与其他入组模式的比较

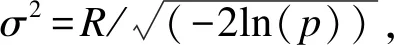
讨 论

