卷烟销量组合预测模型研究

吴明山，王冰，起亚宁，郑飘

1 河南中烟工业有限责任公司，河南省郑州市郑东新区榆林南路16号 450000;

2 国家烟草专卖局烟草经济信息中心，北京市西城区月坛南街55号 100045

随着卷烟营销模式的不断深化，卷烟市场逐步由“卖方市场”向“买方市场”转变，消费者拥有越来越多的选择权，对卷烟销售工作的挑战持续增加，销量预测成为提升卷烟营销水平的一项重要的内容。精准的卷烟预测，可有效消除卷烟供应链中的“牛鞭效应”，有利于烟草工商企业高度协同，提高企业对卷烟需求的把握能力，准确判断需求变化趋势，提升卷烟按订单组织货源水平，加快推动卷烟市场化取向改革。因此，提高卷烟销量预测精度对提升卷烟营销水平具有重大意义。

1 文献综述

传统销量预测方法有很多种，例如经验分析、移动平均、指数平滑、线性回归等[1]，可以一定程度上提高预测精度，这些方法对样本数据本身有特定的要求（样本量足够大或线性相关），但在实际应用中产品销售的历史数据样本量有限或不能完全满足线性规律，预测效果会受到较大影响[2]。由于卷烟销售受季节性和节日因素影响较大，呈现出明显的季节性、周期性特征，其预测值往往与卷烟销售历史具有高度相关性，因此时间序列预测方法更加适合。ARIMA模型就是一种适合数据具有稳定的季节性特征的短期预测方法，具有较强的灵活性[3]，为季度或月度卷烟销量预测，提供了较好的应用价值，预测结果较为可靠[4][5]。但由于其对数据稳定性要求较高，对于非稳定的时间序列的中长期预测精度有待提升。近年来，神经网络模型因其灵活的非线性建模能力、较强的自适应性、学习能力和大规模并行计算能力，被广泛地应用于时间序列预测研究中[6]。其中，BP神经网络是应用最多的一种。理论证明，当隐含层神经元数目足够多时,可以以任意精度逼近任何一个具有有限间断点的非线性函数[7]，这一特性使其特别适合于求解内部机制复杂的问题，在销量预测中受到广泛关注。经典BP神经网络算法是基于梯度下降的学习算法[8]，具有较强的自适应能力和容错能力，但其收敛较慢、训练时间较长，容易陷入局部最优，进而影响预测精度。因此，需要对该方法进行优化改进。基于Levenberg-Marquardt算法（LM算法）改进的BP神经网络就是应用最广泛的方法之一，该算法是用模型函数对待估参数向量在其邻域内做线性近似，忽略掉二阶以上的导数项，将优化目标方程转化为线性最小二乘问题，并利用梯度求最值，同时具有梯度法和牛顿法的优点，预测效果得到进一步提升[9]。蒋兴恒等采用基于LM算法改进的BP神经网络对卷烟月度销量进行预测，并与ARIMA预测结果进行比较，结果表明改进后的BP神经网络模型预测效果更好[10]。

单项的预测模型具有各自的优缺点，只能提取数据的部分有效信息，且受设定条件的影响，预测精度仍有较大提升空间[11]。于是，J.M.Bates和C.W.J.Granger提出组合预测方法，该类模型能综合提取不同预测方法的有效信息，它可以克服单一模型的局限性，预测精度得到有效提高[12]。因此，组合模型也开始应用于卷烟销量预测中。朱俊江等通过建立小波变换、回归分析和神经网络算法构成的组合模型对乡镇单位的卷烟销量进行预测，其预测精度要好于ARIMA模型和基于LM算法改进的BP神经网络模型[13]。

组合预测模型的核心有两个：一是单项预测模型的选择，要根据数据的具体特征确定；二是确定各单项模型的权重，其方法可分为两类：一类是固定权重，另一类是动态权重[14]。研究表明，动态权重组合模型比固定权重组合模型具有更高的预测精度[15]。因此，本文根据卷烟月度销量数据非线性、波动性和规律性特征，选择ARIMA模型、基于梯度下降算法的BP神经网络模型、基于LM算法改进的BP神经网络模型作为3个单项预测模型，并利用BP神经网络对各单项预测模型进行动态加权，从而构建非线性组合预测模型，对2006～2017年144个月的全国卷烟销量进行仿真训练，综合提取各单项预测模型的有效信息，以期预测2018年1～4月的全国卷烟销量。

图1 2006～2017年我国卷烟各月销量趋势Fig.1 Monthly sales trend of cigarettes in China from 2006 to 2017

2 卷烟销量预测模型构建与预测

2.1 ARIMA模型

ARIMA模型是由Box和Jenkins提出的一种时间预测方法，该方法将原始时间序列数据看作一个随机序列，并用一定的数学模型来近似描述，一旦被识别后，就可以利用该模型根据历史数据来预测未来。本节以2006～2017年共144个月的全国卷烟销量数据（万箱）作为基础数据，如图1所示，应用MATLAB对其进行ARIMA拟合，并预测2018年1～4月的销量。

2.1.1 数据处理

从销量趋势图中可以看出，该时间序列非平稳，对数列先进行1阶差分处理，将其平稳化，其公式为：

如图2所示，一阶差分的时间序列的均值和方差均基本平稳，接近一个白噪声序列。

图2 差分处理图Fig.2 Differential processing diagram

图3 自相关函数图Fig.3 Autocorrelation function diagram

2.1.2 模型识别与定阶

通过平稳性检验可知，即将建立的ARIMA（p，d，q）模型，其中d=1，其基本公式为：

其中，x为时间序列，θ是常数项，α为自回归系数，β为移动平均系数，μ为白噪声，p为自回归项，q为移动平均项。

为确认模型中p和q的值，以AIC准则为评价该时间序列数据的准则，利用MATLAB进行测试。本次基础数据为144个，故将p和q的范围定为1～29之间，通过测试确定AIC=7.06，p=25，q=7，即选择的模型为ARIMA（25，1，7）。

2.1.3 仿真及预测结果

将p和q的值代入模型，计算得到2006～2017年各月卷烟销量的拟合值（如图4所示），模型拟合度为76.07%，平均绝对误差为14.82，平均绝对误差率（平均绝对误差/平均真实销量，下同）为3.81%，拟合精度整体良好。

将预测长度设定为4个月，利用该模型对2018年1～4月全国卷烟销量进行预测，如表1所示，可以看出预测误差均较大，除1月份外，其余3个月的绝对误差值均大于当月的日均销量。

2.2 基于梯度下降算法的BP神经网络预测模型

BP神经网络是 Rumelhart 和McClellend于 1986年提出一种多层网络的“逆推”学习算法，是一种单向传播的多层前向网络，具有3层或3层以上，包括输入层、隐含层和输出层，其中隐含层可以有多个层次，上下层之间的神经元全部连接，但每层神经元之间相互独立没有连接，其结构如图5所示。当学习样本进入神经网络后，神经元的激活值从输入层经过各隐含层传向输出层，若达不到期望，则进入误差反向传播过程，逐次调整网络各层的权值和偏置，最后回到输入层，再重复计算，通过不断调整各层的权值和阈值，从而达到网络误差最小，学习过程结束；再利用训练好的网络进行预测。

BP神经网络通过训练误差来逐步调整各层间的输入权重和偏置，这个调整过程的算法依据为最基本的梯度下降法（Gradient Descent），由于训练误差是关于输入权重和偏置的二次函数，分别对权重和偏置求偏导数，即梯度向量，沿着梯度向量的方向，是训练误差增加最快的地方，而沿着梯度向量相反的方向，梯度减少最快，在这个方向上更容易找到训练误差函数（损失函数）的最小值。本节利用MATLAB软件应用梯度下降算法的BP神经网络对全国卷烟历史销量数据进行训练并预测，其处理步骤如下：

图4 ARIMA模型对2006～2018年4月全国卷烟销量的拟合及预测图Fig.4 The fitting and forecasting of national cigarette sales from 2006 to April 2018 by ARIMA model

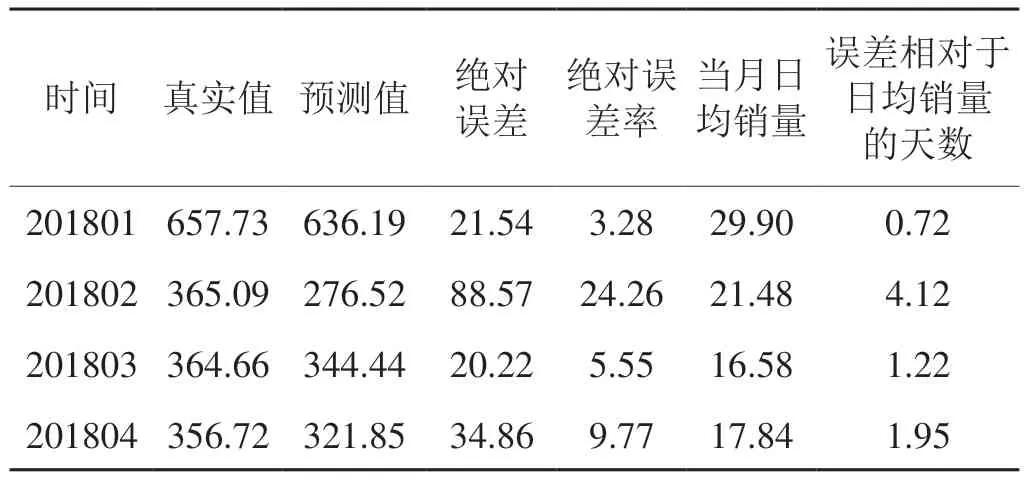
表1 ARIMA模型对2018年1～4月全国卷烟销量预测表Tab.1 National cigarette sales forecast for January-April in 2018 by ARIMA model万箱，%，天

图5 典型BP神经网络模型结构Fig.5 Structure of typical BP neural network model structure

2.2.1 样本数据确定

由于卷烟销量执行的是年度计划，为更好的反应卷烟销量的时间特点，本文将2006至2017年每12个月销量数据作为一组输入向量，形成12*129的输入矩阵；以之后4个月的销量数据作为网络的输出，形成4*129的输出矩阵，用神经网络进行训练。

2.2.2 样本数据处理

数据的预处理和后处理是训练神经网络的关键步骤，它直接影响到训练后神经网络的性能，常见的方法是将原始数据进行归一化处理，即通过一定的线性变换将输入数据和输出数据统一限制在[0,1]或[-1,1]区间内。本节选择最大最小法进行处理，其函数形式是：

其中，xmin为数据序列的最小值，xmax为数据序列的最大值。最大最小值法可以通过MATLAB的mapminmax函数对数据进行处理，让其落入在[-1,1]区间内。

2.2.3 创建网络及参数设定

本模型设计主要涉及到网络的层数、每层中的神经元个数和激活函数、初始值以及学习速率等几个方面。

（1）网络层数确定。理论证明，具有偏差和至少一个S型隐层加上一个线性输出层的网络，能够逼近任何有理函数，增加层数可以进一步降低误差，提高精度，但同时也使网络复杂化。本节模型选择3层网络，即1个输入层、1个隐含层、1个输出层。

（2）创建网络。在MATLAB中创建神经网络要确定以下函数：①输入层和隐含层的传递函数采用正切S型函数，以tansig表示，即：

②输出层的传递函数采用线性函数，以purelin表示；③网络训练函数采用动量反转和动态自适应学习率的梯度下降算法训练函数tianingd；④确定隐含层神经元个数，理论上没有计算出多少隐含层节点最合适，在具体设计时，要通过对不同神经元数进行训练比较，以网络最小误差为依据确定神经元数。通过循环计算，确定此模型的神经元个数为9个。

（3）网络训练参数设定。①根据梯度下降法的特点，训练次数选取为80000；②误差性能目标值选取为0.01；③学习速率一般取值范围为0.01-0.8之间，学习速率太大可能导致系统的不稳定，但学习速率太小导致收敛太慢，需要较长的训练时间，为达到目标误差精度，此模型选取0.01。

2.2.4 仿真及预测结果

利用基于梯度下降算法的BP神经网络预测模型对卷烟销量数据进行训练和仿真，如图6所示，经过79976次训练之后达到目标误差0.01的要求，模型拟合效果如图7所示，其平均绝对误差为17.87，平均绝对误差率为4.59%，其拟合精度不及ARIMA模型。

图6 基于梯度下降算法的BP神经网络训练图Fig.6 BP neural network training diagram based on gradient descent algorithm

图7 基于梯度下降算法的BP神经网络对2007～2018年4月全国卷烟销量的拟合及预测图Fig.7 Fitting and forecasting of national cigarette sales from 2007 to April 2018 by BP neural network model based on gradient descent algorithm

输入2017年12个月的卷烟销量数据，模型得到2018年1～4月销量的预测值，如表2所示，可以看出虽然该模型拟合效果不及ARIMA模型，但预测结果要明显好于ARIMA模型，除2月份由于春节因素导致预测效果较差外，其余月份预测结果十分逼近真实销量，均不足半天的当月卷烟销量。

表2 基于梯度下降算法的BP神经网络对2018年1～4月全国卷烟销量预测表Tab.2 Forecasting of national cigarette sales volume from January to April in 2018 by BP neural network based on gradient descent algorithm万箱，%，天

2.3 基于Levenberg-Marquardt算法改进BP神经网络的预测模型

从上述基于梯度下降算法的BP神经网络模型训练过程发现，虽然该模型能较好的拟合卷烟销量并比较准确的预测未来4个月的销量，但其学习算法的收敛速度较慢，训练次数达到了近8万次，另外其预测误差精度较低，仅能达到0.01。针对该模型存在的不足，出现了几种基于该模型的改进算法，如拟牛顿法、Levenberg-Marquardt算法（简称LM算法）等。通过实验发现，对中小规模的神经网络，使用LM算法的收敛速度最快，且计算精度较高。作为BP神经网络的改进算法，LM算法实际上是梯度下降法和高斯牛顿法的结合，该算法期望在不计算Hessian矩阵的情况下获得高阶的训练速度，其公式表达为：

其中，J为雅克比矩阵，e是网络误差向量。随着 越来越小，该算法越来越接近高斯牛顿法；随着越来越大，该算法越来越接近梯度下降法。由于高斯牛顿法收敛速度更快更准确，因此LM算法的目的就是尽快接近高斯牛顿法，如果某次迭代成功，误差减小，则减小 的值；如果迭代失败，则增加 的值，从而使得误差性能函数随着迭代的进行而下降到极小值。

2.3.1 基于LM算法改进BP神经网络模型构建

基于LM算法改进BP神经网络模型的输入向量和输出向量与基于梯度下降算法的BP神经网络模型相同，并进行归一化的数据处理，确定网络层数，选择传递函数，设定训练次数、训练精度、学习速率等参数。但与前者不同的是，基于LM算法改进的BP神经网络模型需要将模型的训练函数更改成LM算法，在MATLAB中以trianlm表示。鉴于LM算法快速、准确收敛的特点，将模型训练次数取为3000，误差性能目标值取为0.0005，学习速率仍为0.01，经过测试神经元数量取为30个。

2.3.2 仿真及预测结果

利用LM算法改进BP神经网络模型对卷烟销量数据进行训练和仿真，如图8所示，经过32次即可达到目标误差0.0005的要求，模型拟合效果明显更好，如图9所示。其平均绝对误差为3.99，平均绝对误差率为1.03%，其拟合精度明显高于ARIMA模型和基于梯度下降算法的BP神经网络模型。

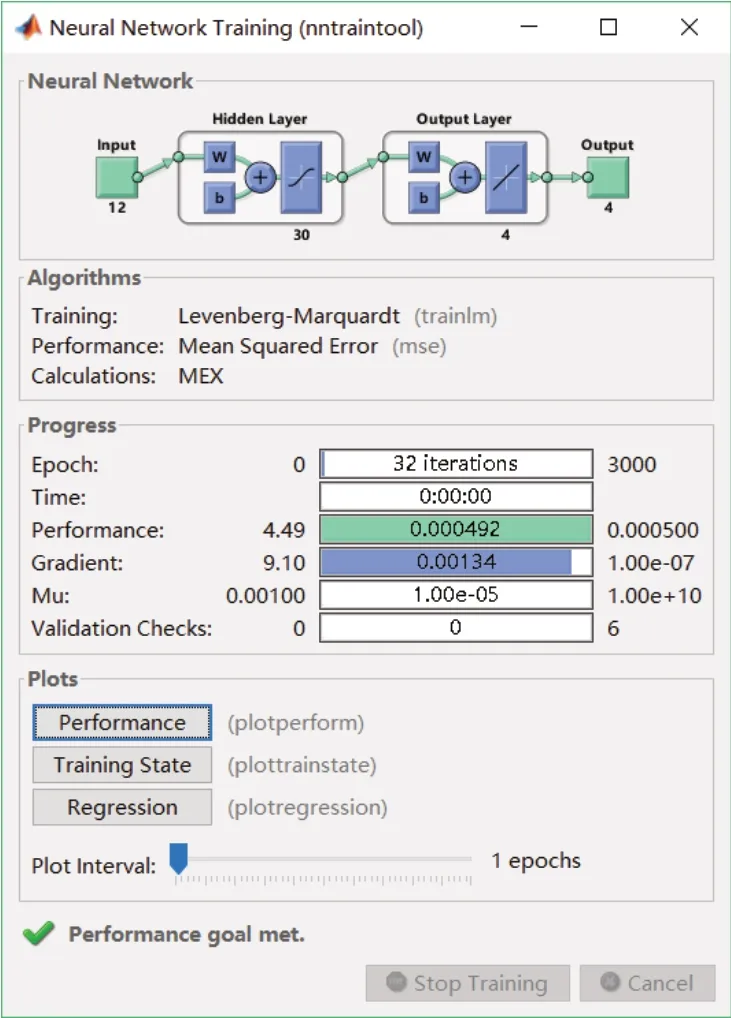
图8 基于LM算法的BP神经网络训练图Fig.8 BP neural network training diagram based on LM algorithm

输入2017年12个月的卷烟销量数据，从而得到2018年1～4月销量的预测值，如表3所示，可以看出经过改进后的BP神经网络模型，预测误差更加均衡，其预测效果更加平稳，适应性更强。

图9 基于LM算法的BP神经网络模型对2007 ～ 2018年4月全国卷烟销量的拟合及预测图Fig.9 Fitting and forecasting of national cigarette sales from 2007 to April 2018 by BP neural network model based on LM algorithm

表3 基于LM算法的BP神经网络模型对2018年1 ～ 4月全国卷烟销量预测表Tab.3 Forecasting of national cigarette sales forecast for January-April in 2018 by BP neural network model based on LM algorithm万箱，%，天

2.4 非线性组合预测模型构建与预测

上述3种模型均在一定程度上解释了卷烟销量数据之间的联系，并对未来4个月的卷烟销量进行预测，但单项预测方法存在未能充分利用历史数据的缺点，从而导致预测结果不够精准，为此，通过构建非线性组合预测模型，吸收各模型的优点，提高预测精度。

2.4.1 模型构建思路

本节通过基于LM算法改进的BP神经网络构造非线性组合模型，其构建思路为：（1）以ARIMA模型拟合值、基于梯度下降算法的BP神经网络拟合值、基于LM算法的BP神经网络拟合值作为输入向量，即选取相同月份的3种模型拟合值作为输入向量，当月真实销量作为输出向量，进行训练后进行仿真拟合；（2）输入上述3种模型对2018年1～4月全国卷烟销量的预测值，得到组合预测模型对销量的预测结果。

2.4.2 模型参数设定

对销量数据的训练参数设定为：训练次数取为3000，误差性能目标值取为0.0005，学习速率为0.01，经过测试神经元数量取为30个。

2.4.3 仿真及预测结果

通过训练，组合预测模型训练的销量数据经过4次达到目标误差精度0.0005的要求，如图10所示，模型拟合效果明显更好，如图11所示。其平均绝对误差为3.3，平均绝对误差率为0.85%，其拟合精度均高于上述3种模型。

图10 组合预测模型的销量数据训练图Fig.10 Sales data training chart of combined forecasting model

图11 非线性组合预测模型对2007～2018年4月全国卷烟销量的拟合及预测图Fig.11 Fitting and forecasting of national cigarette sales from 2007 to April 2018 by nonlinear combination forecasting model

输入上述3种模型对2018年1～4月销量的预测值，利用训练好的模型得到组合预测模型对2018年1～4月销量的预测值，如表4所示，可以看出组合预测模型的预测绝对误差较为均衡，均不足1天的当月日均销量。

2.5 模型预测效果对比

对比4种模型的预测值，发现各预测模型呈现不同的特点：ARIMA模型预测近期销量相对较准，但较远月份的预测值误差较大；基于梯度下降算法的BP神经网络模型可以较为准确的预测大部分月份的卷烟销量，但对于波动性较大的月份预测误差较大；基于LM算法的BP神经网络模型作为改进后的神经网络模型，预测结果精度更高，预测误差更为平稳；非线性组合预测模型综合利用上述3种模型的优点，有效提取数据各方面信息，预测绝对误差均小于当月的日均量，其预测结果最为平稳，适应性最强，更加贴合卷烟销售实际情况。

表4 非线性组合预测模型对2018年1～4月全国卷烟销量预测表Tab.4 Forecasting of the national cigarette sales from January to April in 2018 by nonlinear combination forecasting model万箱，%，天

表5 四种模型对2018年1～4月全国卷烟销量误差值对比Tab.5 Comparison of error values of national cigarette sales from January to April in 2018 by four different models 万箱，天

3 结论

本文选择ARIMA模型、基于梯度下降算法的BP神经网络模型、基于LM算法改进的BP神经网络模型作为3个单项预测模型，并利用BP神经网络对各单项预测模型进行动态加权，从而构建非线性组合预测模型，对2006～2017年144个月的全国卷烟销量进行仿真训练，并对2018年1～4月的卷烟销量进行预测。通过对比表明，非线性组合模型具有更好的预测效果，对卷烟调拨计划制定，科学安排生产计划等具有一定的参考意义。此外，该模型的构建思路还可用于卷烟各价类的销售预测。

同时，在研究过程中，发现由于春节及政策的影响，每年1月份的卷烟销量远高于其他月份，2月份销量迅速下降，致使1、2月份的差值非常大，数据极具波动性，极易造成预测误差。因此，后续研究中，可以引入月度调节因子、政策影响因子等调整因素，以期进一步提高预测精度。