刚性球体三维高速垂直自由入水载荷*

孙玉松，周穗华，张晓兵，孙玉明

（1. 海军工程大学兵器工程学院，湖北 武汉 430033；

2. 91267 部队，福建 福州 350000）

水上飞机、航天器、鱼雷、水雷等入水均属非周期性入水问题，有着广泛的应用前景，是流体力学领域内研究的重要内容。自1929 年von Karman 提出忽略浮力，采用动量定理对楔形体以及平头体入水载荷进行计算后，Wagner[1]将von Karman 的方法进行了更为详细的推导，考虑到水面抬升，提出了基于小斜升角模型的近似平板理论。May 等[2]分析了入水初期流体流动特点，得出了钢球入水初期的入水载荷系数。Korobkin 等[3]考虑结构体的弹性，在每一个时间步内首先求解结构体受力，而后根据结构体压力分布求解其变形，是一种耦合度较高的计算方法。关于入水初期结构体载荷问题的理论研究基本遵循Wagner 渐进匹配近似理论，该理论主要针对可等效为二维结构体的入水模型，当流体三维流动特性较为明显时，需引入修正系数对该方法进行修正[4-5]。宋保维等[6]和王永虎等[7]建立了六自由度的水雷水下弹道模型，依据不可压缩流体非定常势流理论和镜像法求解入水载荷，并应用于大型弹体以约60 m/s 速度入水的计算中。孙士丽等[8]采用三维全非线性不可压缩势流理论方法研究了有限水深中非轴对称体的斜向入水抨击问题，对轴对称体与非轴对称体的垂直入水以及斜入水进行了模拟。

随着数值方法的发展并在流体流动问题上的应用，工程上大量复杂流动问题得以解决，王健等[9]、马庆鹏等[10]和朱珠等[11]使用基于网格的数值方法对结构体入水过程进行了仿真，并对入水载荷进行了分析。Oger 等[12]采用光滑粒子流体动力学方法（SPH），计及入水过程中流体的可压缩性，计算了作用在刚体上的压力。虽然数值方法已能有效解决大部分的工程问题，但对于从本质上解释入水冲击这一现象的意义有限。本文中所研究的刚性球体以160～240 m/s 的速度垂直入水，流体的运动是一个非定常的三维流动，且持续时间极短，撞水瞬间流体呈现出较强的弹性效应，并产生振动[13]。由于入水载荷极大且持续时间极短，重力作用和流体黏性作用均可忽略。液体不可压缩，但需考虑其弹性，认为小幅度的弹性对于流体的不可压缩性影响很小，在无黏不可压流体流动模型的基础上，采用微元边界运动等效方法对运动边界进行分段分析，计及入水过程中系统的动能损失，根据能量守恒，对刚性球体垂直入水初期流体的三维运动进行分析，求出刚性球体入水过程中的载荷。

1 刚性球体垂直入水动力学方程

刚性球体在入水初始时刻的位置示意图如图1 所示。

对于一个以速度Vp在Z 轴方向上运动的刚性球体来说，为了计算它的入水载荷，首先需要写出其动力学方程。根据牛顿第二定律，刚性球体的动力学方程为：

图 1 刚性球体位置示意图Fig. 1 General view of the rigid sphere’s location

式中：m 为刚性球体的质量，F 为其入水阻力。

目前计算入水阻力的一个普遍采用的计算公式为：

式中：ρ 为水的密度，Av为刚性球体的最大截面积，Cd为与速度相关的阻力系数。

根据Charters 及Thomas 测量的阻力系数与入水速度的关系可以分为3 个区间，入水速度在亚声速到Ma=0.5 区间时，Cd=0.384。式(2)在刚性球体对周围流体形成完全扰动之后是有效的，但在扰动形成阶段，该公式计算得到的结果严重偏小，Wagner 理论正是用于计算该过程的，自提出以来，围绕该理论取得了较为丰硕的成果[14]，但基于Wagner 理论的方法在讨论三维流动问题时往往是按照二维入水问题计算，然后添加修正系数[15]，本文针对Wagner 理论所存在的不足，采用刚性球体微元边界运动等效的方法考虑三维效应，对刚性球体的入水载荷进行计算。

2 刚性球体垂直入水载荷计算模型

刚性球体高速垂直入水时，背部将会形成空泡，假设入水深度过半球时流体与球体分离，未触水部分无表面阻力。从球体触水至触水面发展完全这一撞水阶段，由于撞水时间持续极短，流体黏性作用有限，因此将流体看作无黏流体，Lee 等[16]在研究高速入水条件下的弹道波的时候使用可压缩波动方程和不可压缩伯努利方程（非定常流动的伯努利方程），虽然看起来是前后矛盾的，但依然取得了非常好的结果。可以认为，在刚性球体高速入水的条件下，流体中有限的弹性对于流体的不可压缩特性影响不大，本文模型是建立在无黏不可压弹性流体基础上的。

如图2 所示是四分之一球体剖面由OMM′运动到O′NN′。

将弧边MM′进行分割，任意两相邻点Mi 与Mi+1 组成微元边界MiMi+1，MiMi+1 所代表的微元面在空间上的位置如图3 所示。

图 2 球体入水运动示意图Fig. 2 General view of sphere’s micromovement

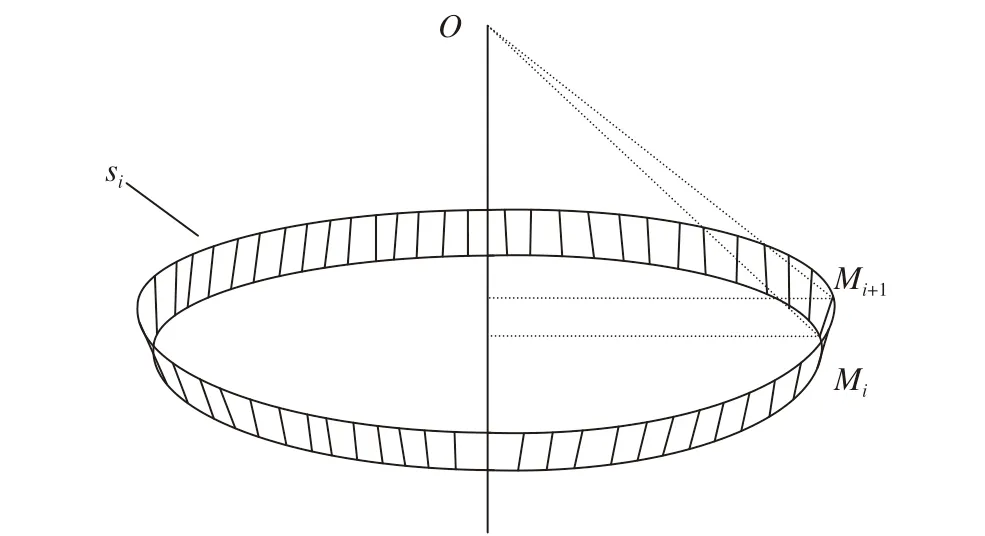
图 3 弧段微元示意图Fig. 3 General view of a microsegmental arc

图中阴影部分即是弧段MiMi+1所代表的空间上的微元面si，弧段MiMi+1即是刚性球体截面圆的微元边界，为了表达的方便，下面以微元边界MiMi+1指代微元面si进行表述。

微元面s 的面积为dSi，表达式为：式中：δh 为微元边界MiMi+1在竖直方向上的投影；θ 为OMi与OM 的夹角；R 为球体半径。

过圆心O 分别与Mi、Mi+1连线并延长，与弧线NN'分别相交于Ni、Ni+1，如图4 所示。由于流体无黏且不可压，可认为弧段MiMi+1通过扩张到达NiNi+1。采用此等效方法，会使得水面附近的弧段在弧线NN'上无对应区域，当L 极小时，此部分弧长趋于0，可将其忽略。

设MiMi+1表面流体的等效扩张速度大小为vi，表达式为：

微元边界MiMi+1在δt 时刻后扰动的流体区域示意图如图5 所示。

CiCi+1为在微元边界MiMi+1作用下流体受迫运动产生的扰动波波面，波面的扩张速度为声速c，波面CiCi+1后部的流体处于未扰动的状态，速度为0。根据弹性理论，波的传播速度为声速c，则此刻波面距离运动的球心O 的距离Rci的表达式为：

式中：t 为系统时间；ti为微元边界MiMi+1触水时间。经过δt 后，新增扰动区域内流体质量δmθ的表达式为：

图 4 微元边界运动等效示意图Fig. 4 General view of microboundary’smotion equivalent

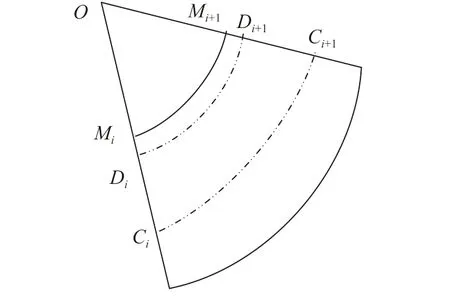
图 5 微元边界扩张示意图Fig. 5 General view of microsegmental arc’s expansion

当δt 足够小时，可认为新增扰动区域内流体速度大小相等，设该区域内流体平均速度为vci，根据不可压缩流体流动的连续性，可知vci的表达式为：

δmθ的动能增量δEθ可以表示为：

根据动量守恒，可知δmθ在垂直方向上的动量增量δMθ可以表示为：

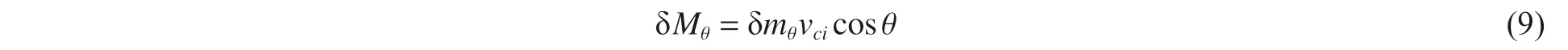
设δt 时间内作用在δmθ上的力为Fci，平均值为 Fci，根据动量定理，则 Fci可以表示为：

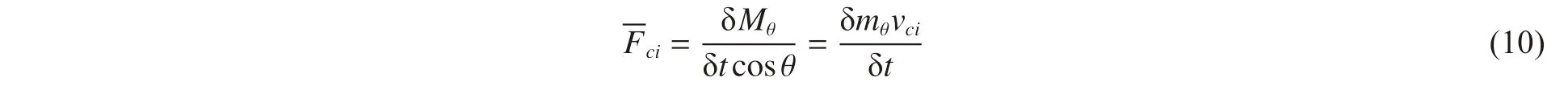
在微观层面，Fci是变化的，但作用面的位移速度为vci，则力Fci在δt 时间内做的功δWi可以采用平均力 来计算，即：

在δt 时间内，刚性球体的每一个微元边界对流体做的功是流体动能增加量的两倍，损失的能量将主要以波的形式不断扩散出去。根据能量定律，在δt 时间内，刚性球体的动能损失量dE 应等于各个微元边界对流体做功的总和，dE 的表达式为：

δt 时间内，刚性球体受到的合外力F 的表达式为：

刚性球体入水载荷，即入水加速度a 的表达式为：

随着刚性球体入水深度的增大，以对流体扰动作用为主的Wagner 阶段逐渐结束，本文所建立的模型便不再适用，后期刚性球体入水阻力F 的表达式为：

式中：Cd是随速度变化的，在本文中，Cd=0.384。

从Wagner 阶段结束到可使用经典入水阻力表达式之间的过渡阶段流体流动较为复杂，这里进行近似处理，当采用经典入水阻力表达式计算得到的球体入水阻力Fc大于本文模型计算得到的入水阻力FR时，便使用经典的入水阻力表达式计算入水载荷。

综上所述，刚性球体垂直入水载荷表达式为：

3 模型验证

刚性球体高速入水是强非线性过程，涉及固、液、气三相的运动，采用多介质ALE 方法对刚性球体入水冲击过程进行数值计算。

为了节省计算量，根据对称性，采用四分之一模型对入水过程进行计算，计算域网格采用八节点六面体单元，空气和水均采用ALE 网格，刚性球体采用Lagrangian 网格，四分之一计算域有限元模型如图6 所示。

定义球体为刚体，水和空气均选用空材料模型，水的状态方程采用Grüneisen 方程，空气则采用线性多项式方程。Grüneisen 方程的压力表达式为：

式中：C=1 480 m/s 为介质中声速；S1、S2、S3为冲击波输入参数，S1=2.56，S2=-1.986，S3=0；μ 为介质压缩比，μ=ρ/ρ0-1，ρ0为常温状态下水初始密度，ρ 为水当前密度；γ0=0.493 4 为Grüneisen 初系数；a 为Grüneisen 系数修正项，为1.393 7；E 为体积内能。

图 6 有限元模型Fig. 6 Finite element model

线性多项式（Linear_polynomial）状态方程的压力表达式为：

式中：μ=ρ/ρ0-1，E 为体积内能，C0=C1=C2=C5=C6=0，C3=C4=0.4。

设置过球体剖面的两个面为对称边界面，其余面为非反射边界面。采用罚函数方法进行流固耦合。球体半径为0.2 m，质量为261 kg，入水速度为200 m/s。经过计算得到球体入水载荷曲线如图7所示。

对于有限元仿真结果的验证一般采用试验的方法，但大型球体高速入水所需动能极大，实验室内难以达到相应的试验条件，且在高速入水条件下，结构体入水载荷难以准确测量，而入水空泡的外形容易观测，入水空泡与能量转化量直接相关，仿真模型的准确性可以通过对比空泡的外形来验证[17,18]。在入水空泡的研究方面，May 等[19]通过大量的试验观察得到入水初期入水空泡轮廓除头部以外可近似为抛物线，顾建农等[20]对此进行了进一步验证，抛物线的方程为：

式中：h 为入水深度；CD为结构体入水阻力系数；db为入水结构体特征尺寸，本文中为球体直径。

在当前入水条件下，基于有限元模型和May的空泡模型得到的入水空泡轮廓对比结果如图8所示。

可知除触水部分外，两种方法计算得到的空泡轮廓一致，因此使用该有限元方法和参数计算刚性球体入水冲击过程是准确可行的，可使用该有限元方法对式（16）所表示的理论方法进行验证。

有限元方法与理论方法分别得到的刚性球体入水载荷曲线对比结果如图9 所示。

理论方法与有限元方法分别求得的入水载荷峰值相差15.2%，入水载荷峰值出现的时间相差32%。为进一步验证理论方法的合理性，下面使用两种方法分别对质量为391.5 kg 以及入水速度为240 m/s时钢球的入水载荷进行计算，结果见图10 和图11。

此入水条件下，入水载荷峰值相差14.4%，入水载荷峰值出现的时间相差29.4%。

此入水条件下，入水载荷峰值相差18.7%，入水载荷峰值出现的时间相差18.2%。

图 8 入水空泡轮廓对比图Fig. 8 Comparison of the cavities

图 9 入水载荷对比图Fig. 9 Comparison of water-entry impact

图 10 球体质量为391.5 kg 时入水载荷对比图Fig. 10 Comparison of water-entry impact when the sphere’s mass is 391.5 kg

图 11 入水速度为240 m/s 时入水载荷对比图Fig. 11 Comparison of water-entry impact when initial velocity is 240 m/s

由图9～11 可知，本文所建立的理论模型得到入水载荷峰值结果偏小，峰值出现时间偏晚，由于该理论模型未考虑入水冲击过程中产生的水堆，水堆的出现使得球体周围等效水面抬升，导致入水冲击载荷峰值时间的提前。同时由于理论模型均匀化了流体内部复杂的压力波动，因此计算结果也较为平缓，峰值宽度也较大。

同时可以看出本文所建立的理论方法得到的入水载荷有一个明显的拐点，这是由于随着入水深度的增加，刚性球体对周围流体的扰动已不是入水阻力形成的主要原因，刚性球体入水过程中阻力所做的功主要转化为排开流体的动能，入水阻力主要成因的转换使得入水过程存在一个过渡的区域，本文对过渡区域进行了简化，当采用经典入水阻力方程计算得到的入水阻力较大时，便采用经典入水阻力方程计算入水载荷，由于计算模型的不同，导致了拐点的出现。

但总体来看，理论方法和有限元方法计算结果一致性较好，该理论模型能够反映出刚性球体入水过程中载荷的主要影响因素。

4 变参数分析

为探究影响入水载荷的因素，本文采用控制变量法，计算不同质量，不同体积，不同入水速度条件下的入水载荷并进行对比分析。

4.1 变质量分析

对体积和入水速度相同，质量分别为130.5、261 和391.5 kg 的刚性球体入水过程中的入水载荷进行计算，并对结果进行比较，结果如图12所示。

由图12 可知，随着刚性球体质量的增加，入水载荷峰值将显著降低，峰值持续时间变化较小。不同质量条件下刚性球体入水载荷峰值如表1 所示。

由表1 可知，其它条件不变时，入水载荷峰值与刚性球体质量呈反比关系。

4.2 变体积分析

将密度和入水速度相同，半径分别为0.1、0.2 和0.3 m 的刚性球体代入模型中进行计算，由于体积（半径）的改变，密度相同的条件下，刚性球体质量也会发生变化，计算得到的3 个刚性球体入水载荷如图13 所示。

图 12 入水载荷对比图Fig. 12 Comparison of water-entry impact

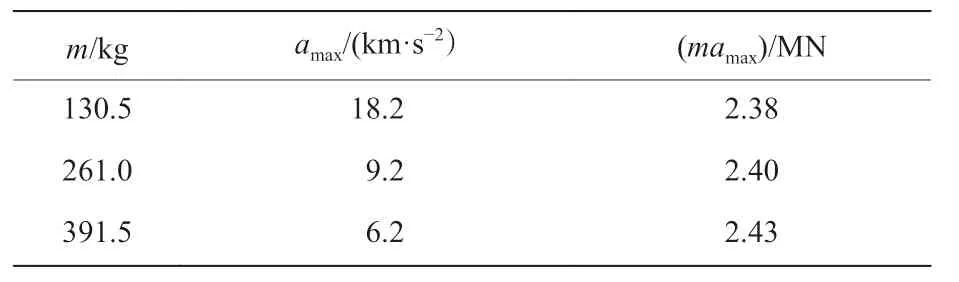
表 1 入水载荷峰值对比Table 1 Comparison of the water-entry peak impact

由图13 可知，随着体积的增大，刚性球体入水载荷峰值降低，且峰值持续时间显著增大。不同体积条件下入水载荷峰值如表2 所示。

表 2 入水载荷峰值对比Table 2 Comparison of the water-entry peak impact

由表2 可知，在刚性球体密度不变的条件下，其入水载荷峰值与半径成反比例关系。

4.3 变速度分析

将质量和体积均相同，入水速度v 分别为160、200 和240 m/s 的刚性球体代入计算模型，得到3 种不同入水速度条件下刚性球体入水载荷如图14 所示。

由图14 可知随着入水速度的增大，入水载荷峰值的增大比较显著，但峰值持续时间会有所缩短。不同入水速度条件下刚性球体入水载荷峰值如表3 所示。由表3 可知，入水载荷峰值与入水速度的平方近似成线性关系。

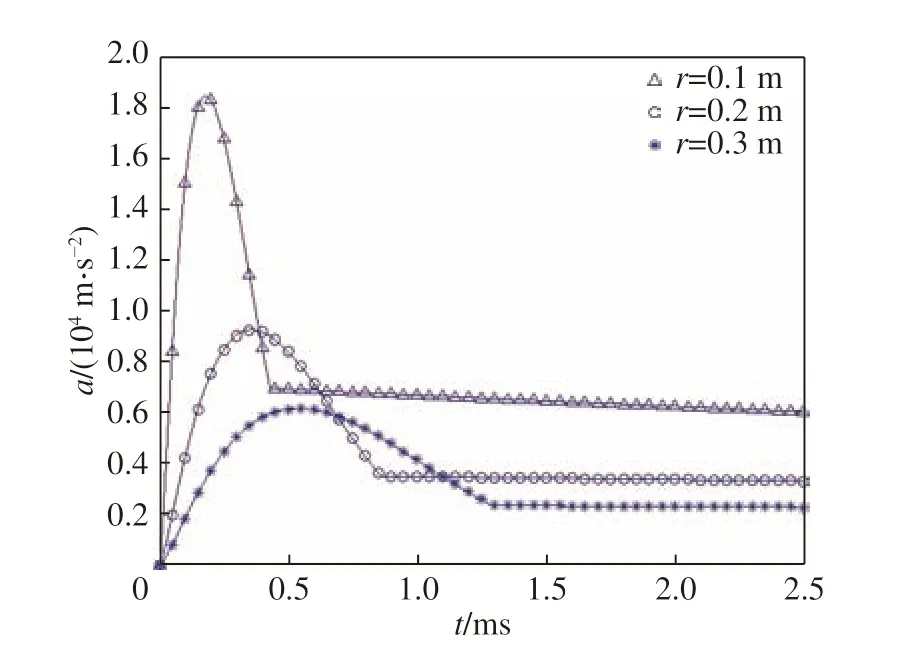
图 13 入水载荷对比图Fig. 13 Comparison of water-entry impact

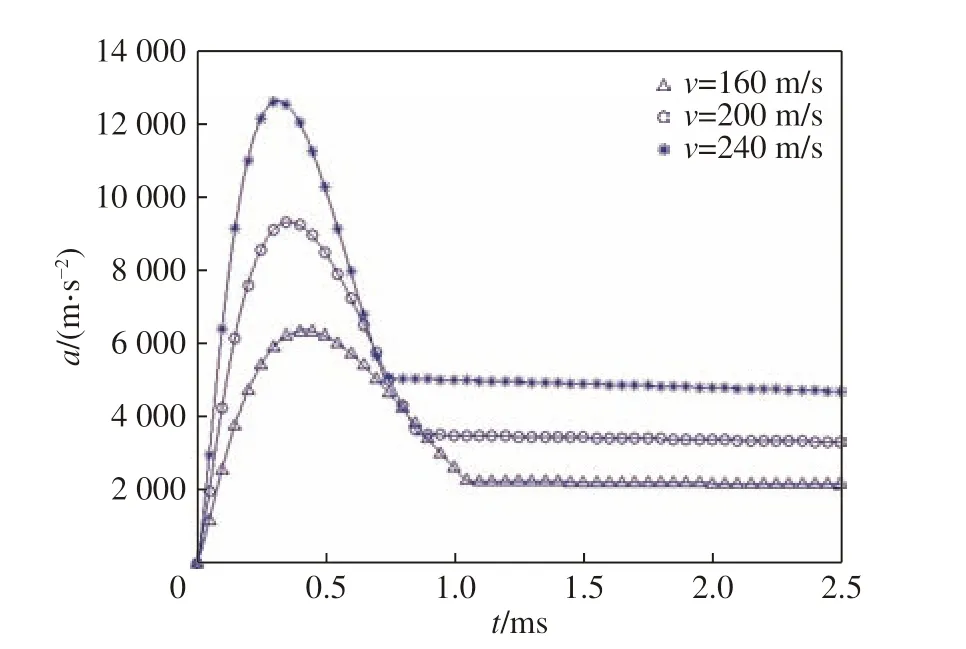
图 14 入水载荷对比图Fig. 14 Comparison of water-entry impact

表 3 入水载荷峰值对比Table 3 Comparison of the water-entry peak impact

5 结 论

本文中基于无黏不可压流体流动模型，考虑流体弹性，采用微元边界运动等效方法对运动边界进行分段分析，计及入水过程中系统的动能损失，根据能量守恒定理，对刚性球体高速垂直自由入水过程中流体的三维流动进行了理论分析，建立了基于无黏不可压弹性流体的刚性球体垂直高速入水载荷计算模型，并验证了该方法的可行性。基于此模型，进一步分析了刚性球体质量、半径以及入水速度对入水载荷的影响，结果表明：

（1）基于无黏不可压流体流动模型，考虑流体弹性，采用边界运动等效方法对运动边界进行分段分析对刚性球体入水载荷进行计算是可行的；

（2）入水载荷峰值与刚性球体质量呈反比关系。随着刚性球体质量的增大，峰值持续时间变化较小；

（3）入水载荷峰值与等密度刚性球体的半径成反比例关系。随着刚性球体体积的增大，入水峰值降低，且峰值持续时间显著增长；

（4）入水载荷峰值与刚性球体入水速度的平方近似成线性关系。随着入水速度的增大，峰值持续时间会有所缩短。