基于全量理论的客车侧翻一步碰撞快速算法＊

王童

（长安大学，西安 710064）

主题词：客车 侧翻 全量理论 一步碰撞快速算法

1 前言

公共交通的迅猛发展，使客车成为当今社会最主流的公共交通工具[1]。同时，客车重大交通安全事故发生率也呈逐步上升趋势，其中侧翻是客车最严重的事故类型之一，给人类生命财产带来了巨大损失[2]。

客车侧翻碰撞结构的变形特点与金属板料冲压成形相似，整个侧翻碰撞过程也为塑性大变形过程，且该过程的变形程度远低于金属板料冲压成形，因此可将金属板料冲压一步成型快速模拟算法应用于客车侧翻数值模拟，在理论上可获得比冲压成形更理想的结果，更具工程应用价值。基于此，本文提出了一种新的客车侧翻一步碰撞快速算法（下称侧翻一步碰撞算法），该算法主要应用于客车结构设计初期，在基本保证工程计算所需精度的前提下，快速获得侧翻碰撞结构的最终变形，进而对客车结构侧翻安全性能进行快速评价，缩短产品开发周期，降低研发成本，为后续针对客车侧翻碰撞安全性的灵敏度分析、参数优化及拓扑优化算法研究提供支撑条件。

2 侧翻一步碰撞算法基本原理

尽管客车侧翻碰撞过程通常发生在车辆运动状态，但目前国内各客车企业对于侧翻碰撞安全性能的评价与认证工作是参考GB 17578—2013《客车上部结构强度要求及试验方法》和ECER66法规在准静态条件下进行的[3]，因此，为对企业产品研发具有指导意义，算法研究也参考目前法规标准在准静态条件下对侧翻碰撞过程进行模拟计算。

侧翻一步碰撞算法计算原理为：客车在外力作用下产生侧翻倾角，当倾斜角度超过侧翻临界角后，车身仅在重力作用下开始发生侧翻；忽略整个侧翻碰撞过程的能量损失，整车随车身重心下降释放出的重力势能全部转换为整车动能，而全部动能又在碰撞中无损失地转换为结构形变能。根据客车侧翻碰撞特点，考虑侧翻开始和车身结构最大变形两个状态之间的运动及力学过程，基于简单比例加载假定，对侧翻碰撞过程进行适当简化。整个侧翻碰撞过程满足能量平衡及转换关系，并以能量平衡作为碰撞结束条件，在客车侧翻撞地临界位置计算算法所需的初始解，然后对初始解构型进行接触判断与修正，并采用Newton-Raphson方法对所得变形结构各节点的广义失衡力进行平衡迭代，快速计算变形量从而得到车身结构的最终变形。

3 计算求解过程

3.1 侧翻碰撞过程简化

依据GB 17578—2013标准及ECE R66法规，客车侧翻碰撞试验过程中各铰链及悬架结构近似为刚体状态。根据一步有限元方法的基本思想，同时考虑车身侧翻碰撞过程的运动变形特点和能量转换关系，将侧翻碰撞试验过程分解为两个阶段，如图1所示。

图1 侧翻碰撞计算过程简化

图1中，第1阶段为从开始侧翻临界位置（简称侧翻临界状态）起至侧翻撞地瞬时位置（简称碰撞开始状态），该阶段车身在重力作用下从转台下落，结构未产生变形，主要能量转换方式是车身随重心下降释放的重力势能转换为车身动能；第2阶段为从侧翻撞地瞬时位置起至车身结构最大变形位置，该阶段车身重心下降很小，但车身结构会产生明显变形，主要能量转换方式是车身的动能在碰撞中转换为结构形变能。

该算法重点研究第2阶段，即从碰撞开始状态到最大变形状态之间的力学过程。基于非线性全量理论和比例加载假定，考虑碰撞开始状态和最大变形状态下的车身结构构形，采用Newton-Raphson方法迭代求解，以快速获得结构的最终变形。

3.2 侧翻碰撞计算模型假设

客车侧翻过程为一个自由旋转落体过程，除地面外几乎不受任何约束，理论上可能的变形形态无限多。考虑到侧翻一步碰撞算法的复杂性，针对侧翻碰撞过程两个阶段中的车身运动状态及力学过程，并结合客车侧翻碰撞变形特点，对碰撞计算模型做抽象和简化，以真实反映实际侧翻碰撞过程的主要特征。

第1阶段的主要运动形式为转动，通过分析多个侧翻试验的高速摄影录像数据发现，在车身下落过程中轮胎与转台间滑动非常微小，为方便计算，忽略轮胎与转台间的微小滑动，将第1阶段简化为定轴转动。同时，忽略运动过程中的能量耗散，假定车身随重心下降释放的重力势能全部转换为车身动能。

第2阶段车身重心下降微小，在碰撞载荷作用下产生明显变形，碰撞后一段时间脱离转台滑向地面，车身大部分动能逐渐转换为结构变形。为便于计算，将第2阶段也简化为定轴转动。同时，忽略碰撞过程能量损失，假定车身动能在碰撞中全部转换为结构形变能。

由于第2阶段的车身运动比较复杂，为检验侧翻碰撞计算模型假定的合理性，采用该假定并应用LS-DYNA软件对多款车型进行了仿真分析，并将其与真实的有限元侧翻分析结果及实车试验结果进行了对比，结果表明，简化后的车身结构变形比真实结果略大，但模拟结果与试验结果误差在允许范围内。从工程评估和应用角度考虑，基于该分析结果的设计偏于安全，因此，将客车侧翻碰撞过程的计算模型简化为由开始侧翻临界位置起、在重力作用下绕固定轴旋转下落的定轴转动过程，如图2所示。

图2 侧翻碰撞计算模型假设

3.3 塑形本构关系

侧翻一步碰撞算法整个过程基于非线性大变形塑性全量理论，且基于简单比例加载假定，采用理想变形的理论假设，认为车身结构最终变形中各单元的应变分量与应力分量成比例[4]。由平面应力条件下的Hill各向异性屈服准则及Henchy形变理论，得到侧翻一步碰撞算法的塑性本构关系[5]为：

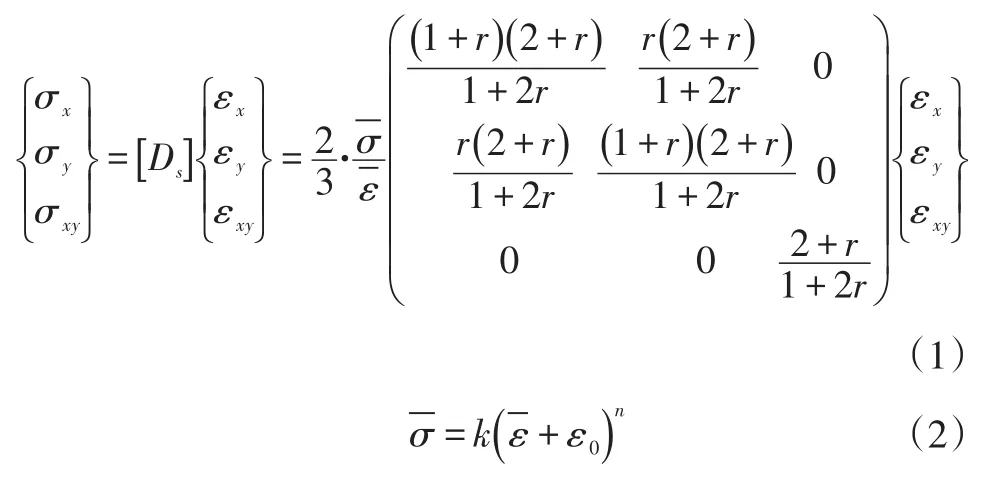
式中，为等效应力；为等效应变；r为材料厚向异性系数；ε0=0为初始应变；k为强化系数；n为应变硬化指数。

3.4 计算分析过程

基于本文假定，在第1阶段结束时刻，即碰撞开始状态下车身结构动能Ed为：

式中，M为车身质量；Δh为车身重心下降高度；J为车身绕假定转轴的转动惯量；ω为车身角速度，g为重力加速度。

碰撞开始状态的车身结构各节点的速度v0i为：

式中，ri为各节点到转轴距离；n′为节点数。

在第2阶段，车身结构主要力学行为是变形。将碰撞开始状态的车身结构作为原始构形｛X0｝，并假定一个最大变形构形｛x0｝，此时各节点的位移｛U0｝为：

车身结构形变能W[6]为：

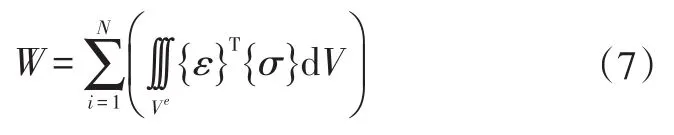
式中，Ve为单元体积；N为单元数；｛ε｝为单元应变；｛σ｝为单元Cauchy应力。

平面应力状态下车身结构大变形几何关系为：

式中，λ1、λ2为Green变形张量下的单元主伸长；θ为λ1与最大变形构形的局部坐标系X轴的夹角。

考虑材料厚向异性的塑性本构计算式为：

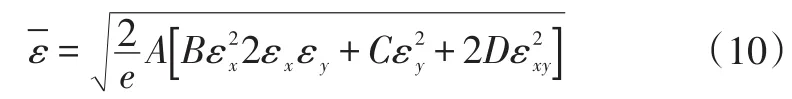
式中，k为强化系数；n为应变硬化指数。

判断车身结构形变能W与车身结构动能Ed是否满足式（16）的能量关系假定：

若不满足式（12），需对节点位移｛U0｝进行修正，按式（7）重新计算结构形变能。将满足式（12）能量关系假定的节点位移｛U｝作为Newton-Raphson迭代初始解。节点位移修正公式为：

式中，γ为修正系数。

与板料冲压一步成型快速模拟算法类似，侧翻一步碰撞算法车身结构在空间内变形过程无外力作用。以上满足能量转换关系的初始解，其节点失衡力｛R（U）｝已处于不平衡状态：

式中，Fex（tU）i为外部力；Fin（tU）i为内部力。

应用Newton-Raphson法解决节点失衡力不平衡问题，对初始解｛U｝按照式（12）迭代求解，使式（14）达到平衡：

切线刚度矩阵为：

式中，η为松弛因子（范围在0～1之间）。

在每个迭代步中，均需对结构整体刚度矩阵[KT(U)]求解，以计算节点广义失衡力极小值，即

满足平衡条件的最大变形构形部分结构可能与地面发生穿透，需要对相应节点进行接触判断，并采用罚函数法对相应节点接触修正。将碰撞接触判断与修正后的结构，按照式（6）～式（19）过程重复进行计算，使得车身结构不与地面发生穿透、结构能量和节点失衡力均平衡，以获得车身结构的最终变形。

4 应用实例

以某长12m的公路客车典型车身段作为分析对象，通过对车身段模型进行适当简化，应用侧翻一步碰撞算法进行侧翻碰撞模拟，将该算法模拟结果与LS-DYNA软件仿真分析结果及实车侧翻试验结果进行对比。

4.1 计算模型

图3为某长12 m的公路客车典型车身段试验模型。依据标准GB 17578—2013及ECE R66法规，按照车身段的实际质量进行配重，车身段由1个简单的翻滚支架固定，最小离地间隙与整车保持一致。典型车身段模型基本参数如表1所列。

图3 典型车身段模型

表1 典型车身段模型基本参数表

车身段侧翻的临界角为39°，参照典型车身段试验模型，简化后的典型车身段结构有限元模型如图4所示，共离散四节点单元261 967个，节点256 136个，外围部分结构为车身骨架结构，底部结构部分为侧翻翻转支架结构，中间部分为乘员生存空间。与侧翻试验模型相同，计算模型骨架及侧翻翻转支架结构材料均选用Q345钢，材料弹性模量E=2.06×1011Pa，泊松比μ=0.3，密度ρ=7 800 kg/m3，屈服强度σs=345 MPa；乘员生存空间为刚性材料；为避免影响侧翻碰撞模拟结果的精度[7]，密度ρ取值尽量小，取ρ=10 kg/m3。

图4 典型车身段结构有限元模型

4.2 结果对比分析

图5为侧翻一步碰撞算法模拟、LS-DYNA仿真、车身段侧翻试验的结果对比。由图5可看出，3种方式获得的车身结构最终变形形态基本吻合，即应用侧翻一步碰撞算法进行侧翻碰撞模拟具有一定工程合理性。

为进一步对车身结构变形进行定量分析，将侧翻试验提供的若干测点作为样本点，在车身段封闭环1和封闭环2两侧立柱上各选取11个测点进行数据采集，得到两侧立柱的变形量情况，并作为与侧翻一步碰撞算法模拟和LS-DYNA仿真分析结构变形的对比数据，测点位置如图6所示。参考侧翻试验中测点选取方式，有限元模型测点的选取位置如图7所示，两点间距离为100mm。

图5 侧翻一步碰撞算法模拟、LS-DYNA仿真、侧翻试验结果对比

图6 侧翻试验测点选取位置

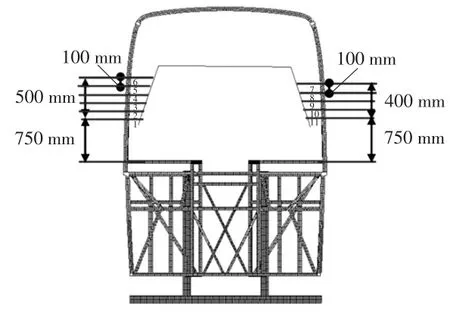
图7 有限元模型测点选取位置

侧翻一步碰撞算法模拟、LS-DYNA仿真及侧翻试验的封闭环1和封闭环2两侧立柱的变形量如表2所列。由表2可知，部分数据存在微小偏差，这是由于受实际侧翻试验制备及测量过程的偶然性影响导致，但误差均在工程允许范围（30%）内。图8为封闭环1和封闭环2两侧立柱的变形量对比柱状图。

表2 封闭环1和封闭环2两侧立柱变形量

图8 封闭环1和封闭环2两侧立柱各测点的变形量对比

从图8可看出，由于受到试验制备及实际测量过程的误差影响，侧翻试验数据在稳定性方面波动相对比较明显，但对于侧翻一步碰撞算法实际应用的有效性检验具有一定工程参考价值。通过对比分析发现，3种方式获得的各测点数据走势基本一致，验证了车身结构最终变形趋势吻合的结论。侧翻一步碰撞算法模拟结果与LSDYNA仿真结果之间的误差平均约为3.1%，精度略有牺牲；与侧翻试验结果的误差平均约为10.4%，小于有限元工程计算误差的经验值范围15%，计算精度在实际可接受范围内。表3为侧翻一步碰撞算法与LS-DYNA仿真的模拟时间对比结果，由表3可知，侧翻一步碰撞算法的模拟时间约为LS-DYNA仿真的1/10，模拟时间较短。

表3 模拟时间对比 min

5 结束语

本文提出了一种客车侧翻一步碰撞快速算法，并利用该算法对某款长12m的公路客车典型车身段进行了侧翻碰撞模拟，并与LS-DYNA仿真及侧翻试验进行了对比，结果表明，3种试验结果中各测点的数据走势基本一致，表明侧翻一步碰撞快速算法可以较好地预测客车结构的侧翻安全性能；该算法模拟结果与其它两种方法之间的误差小于15%，精度在可接受范围内；该算法模拟时长约为LS-DYNA仿真的1/10，在基本保证计算精度的同时使得计算时间大幅缩短。