基于轮系运动学的ZF—9HP自动变速器传动分析

段永彬　张玉芝　阎炳强

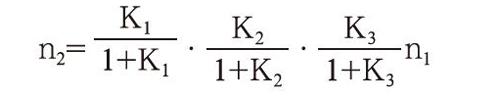
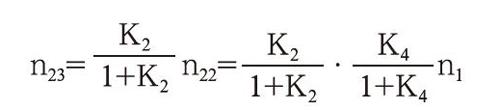
摘 要：ZF-9HP自动变速器是ZF公司近几年推出的新款9速自动变速器。ZF-9HP自动变速器在动力性能，扭矩传输，燃油经济性等方面具有优势，作为未来前驱车辆的最佳选择已应用于多个厂家的多款车上。本文以9HP48为例叙述了ZF-9HP自动变速器各档工作元件，並利用行星齿轮系统传动公式对其各档传动比作了详细的数学分析。

关键词：ZF-9HP；传动比计算

1 引言

传统自动变速器的传动分析较为成熟，计算方法相对简单[1][2][3][4]，对于7速、8速的变速器有图解法[5]、轮系法[6]、杠杆法[7] [8] [9]、表格分析法[10]、图论法[11]等，也有文献提高简化的方法[12]，对于9速度变速器多采用杠杆法分析[13]。

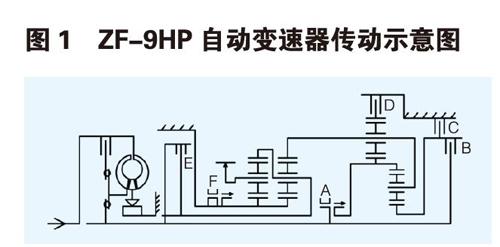
ZF-9HP自动变速器齿轮传动部分含有4套行星齿轮系统、2个制动器C和D、2个离合器和E、2个爪式离合器A和F如图1所示，动力由左侧输入由第一排行星架输出。其结构特殊性在于第三排行星齿轮系统的太阳轮和第四排行星齿轮系统的齿圈是一个整体零件。

ZF-9HP自动变速器电液控制系统通过控制这些元件的工作形成了9个前进档1个倒挡。从左至右各个齿轮系统齿圈齿数对太阳轮齿数的比依次设定为k1、k2、k3、k4。

2 运动分析

2.1 结构参数设置

设：输入转速为n1，输出转速为n2，则：

第一排太阳轮、齿圈、行星架转速依次为n11，n12，n13；

第二排太阳轮、齿圈、行星架转速依次为n21，n22，n23；

第三排太阳轮、齿圈、行星架转速依次为n31，n32，n33；

第四排行星齿轮太阳轮转速、齿圈转速、行星架转速依次为n41，n42，n43；

根据ZF-9HP自动变速器结构可知：

n11=n21，n12=n23，n13=n2

n22=n33=n43，=n42

2.2 各挡传动分析

1档：工作元件为D、F、A，离合器F将第一、二排太阳轮固定，制动器D将第三排齿圈固定，离合器A带动第三排太阳轮旋转，则有：

n1+0-（1+k3）n33=0

对于第二排行星齿轮有：

0+k2n33-（1+k2）n23=0

解方程得：

n23=n33==n1 （1）

对于第一排行星齿轮有：

0+k2n23-（1+k1）n2=0

解方程得：

n2=n23…。…0 （2）

将（1）代入（2）得：

n2=·n1

2档：工作元件C、F、A，制动器C将第四排太阳轮固定，对于第四排行星齿轮则有：

0+k4n1-（1+k4）n43=0

解方程得：n43=n1，对于第二排行星齿轮有：

0+k2n22-（1+k2）n43=0

解方程得：

n23=n22=n1

对于第一排行星齿轮有：

0+k1n12-（1+k1）n2=0

解方程得：

n2=·n1

3档：工作元件B、F、A，离合器B将第四排太阳轮和输入轴固接，对于第四排行星齿轮则有：n1+k4n1-（1+k4）n43=0

所以：n43=n1 n22=n1 对于第二排行星齿轮则有：

n1+k2n1-（1+k2）n23=0

解方程得：

n23=n1

对于第一排行星齿轮则有：

0+k1n23-（1+k1）n2=0，

得：

n2=·n1

4档：工作元件E、F、A，合器E将输入轴与第一排齿圈固接，对于第一排行星齿轮则有：0+k1n1-（1+k1）n2=0

得：

n2=n1

5档：工作元件B、E、A；四排行星齿轮作为一个整体一起旋转。

n2=n1

6档：工作元件C、E、A，对于第四排行星齿轮有：

0+k4n1-（1+k4）n22=0

解方程得：

n22=n1

对于第二排行星齿轮有：

n21+k2n22-（1+k2）n1=0 （1）

對于第一排行星齿轮有：

n11+k1n1-（1+k1）n2=0 （2）

（1）-（2）得：

n2=n1

7档：工作元件D、E、A，对于第三排行星齿轮则有：

n1+0-（1+k3）n33=0 n33=n1

对于第二排行星齿轮则有：

n21+k2n33-（1+k2）n1=0 （1）

对于第一排行星齿轮则有：

n11+k1n1-（1+k1）n2=0 （2）

（1）-（2）得：

在该变速器中，第三排的太阳轮和第四排的齿圈是一个整体零件，在8档和9档传动过程中，第三、四排行星齿轮是共同参与工作的，为了明确第四排的太阳轮、第三排的齿圈、第三、四排行星齿轮的共用行星架在传动过程中的数学关系，如图2所示，作如下分析：

首先设定共用行星架不动，即n3=0，靠近旋转中心的行星轮代码为a，内外齿整体零件代码为b，其内齿数为Zb1，外齿数为Zb2，远离旋转中心的行星轮代码为c，在此参考系中，中心论转速为n1r，最外齿圈转速为：n2r，则有：

以上两式相乘

（1）

两式相乘：

（2）

（1）×（2）得：

令

给行星架附加实际速度n3。则中心轮实际转速为：

n1=n3+n1r n1r=n1-n3；

最外齿圈实际转速为：

n2=n3+n2r n2r=n2-n3

因为，所以：

整理得：

n1-k34n2-（1-k34）n3=0

结论：双行星排齿轮传动公式n1-kn2-（1-k）n3=0仍然适合于第三、四排行星齿轮传动机构，只是k值不同。

8档：工作元件C、D、E，对于第三排和第四排行星齿轮机构则有：

n1-k34·0-（1-k34）n33=0 n33=0

对于第二排行星齿轮则有：

n21+k2·0-（1+k2）n1=0 （1）

对于第一排行星齿轮则有：

n11+k1n1-（1+k1）n1=0 （2）

（2）-（1）：

9档：工作元件D、B、E。对于第三排和第四排行星齿轮机构则有：

n1-k34·0-（1-k34）n33=0 n33=n1

对于第一排行星齿轮则有：

n11+k1n1-（1+k1）n2=0 （1）

对于第二排行星齿轮有：

n21+k2n33-（1+k2）n1=0 （2）

（1）-（2）得：

R档：工作元件D、B、F，对于第三排和第四排行星齿轮机构则有：

n1-k34·0-（1-k34）n33=0

对于第二排行星齿轮有：

0+k2n33-（1+k2）n23=0

（1）

对于第一排行星齿轮则有：

0+k1n23-（1+k1）n2=0 （2）

将（1）代入（2）：

3 结语

ZF-9HP自动变速器用四排行星齿轮和六个换挡控制元件组成，形成了9个前进档和1个倒挡，扩展了传动比的分布，减小了相邻档位传动比的差，这就在传动结构上为换挡平顺性提供了有力条件。

参考文献：

[1]周建东.谈自动变速器中行星轮系的传动比计算[J].重庆职业技术学院学报，2006，15（4）：147-152.

[2]桂乃磐.计算行星轮系传动比求法的比较研究[J].山西机械，2003.（4）：4-5.

[3]高少华.关于典型自动变速器传动比的计算[J].机电技术，2015，（4）：13-15.

[4]黄鹏.行星轮系传动比的快速确定[J].机械工程师，2004，（7）：42-43.

[5]Y尤 扬，尤明福，侯国强.基于图解法的4T65E自动变速器传动分析[J].现代机械，2015，（1）：32-36.

[6]刘志刚，谭火南.组合行星轮系自动变速器传动比计算方法[J].企业技术开发，2013，32（8）：46-47.

[7]李志伟，甘 伟，高奇峰等.基于杠杆法的4T65E自动变速器传动研究[J].大众科技，2013，15（11）：94-98.

[8]尤明福，李志偉，甘 伟.基于杠杆法的8速自动变速器传动方案的设计[J].中国机械工程，23（23）：2801-2804.

[9]贾振华，郏国中，无心平.基于行星轮的8速自动变速器传动比计算[J].汽车实用技术，2011（9）：39-41.

[10]张琳.行星轮系的表格分析法[J].机械传动，1998，22（2）：46-47.

[11]肖丽萍，秦曼华.基于图论的行星轮系传动比分析[J].机械工程与自动化，2006，（4）：126-127.

[12]冯 仲，陈甲虎，张华平.复杂行星轮系传动比计算的简化法[J].机械传动，201236（3）：95-96.

[13]李明圣，李 勇，兰 莹.于杠杆法的ZF9速自动变速器传动路线和挡位扩展分析[J].2014，38（4）：146-148.