高温目标辐射亮度比的方向性研究
张雪峰,潘军,蒋立军,王凯,仲伟敬,张文哲
1. 吉林大学 地球探测科学与技术学院,长春 130026;2. 中国铁路设计集团有限公司,天津 300251;3. 西安卫星测控中心 第一活动站,陕西 渭南 714000
0 引言
地物的电磁辐射方向性是多角度遥感的重要内容,热辐射方向性是像元组分温度反演的关键因素[1]。随着定量遥感的发展,二向性反射和热辐射的方向性已经开展了大量的研究,研究方法主要为多角度观测实验及计算机模拟[2]。许多学者针对植被、农作物、土壤提出了相当数量的辐射传输模型、几何光学模型和计算机模拟模型[3-8];而利用短波红外对高温目标发射辐射的方向性研究较少。
对于使用短波红外进行高温目标温度反演而言,潘军[9-10]建立了地表高温目标混合像元能量模型,从像元、端元、材料三个尺度开展了温度反演的研究,结果表明发射率是高温目标温度反演的至关重要因素,其直接影响温度反演的精度。但高温目标发射率的方向性至今缺乏深入研究。
本文建立多角度观测物理模型并进行实验观测。以燃烧竹炭为小面元高温目标,使用一台ASD FieldSpec3在暗室条件下对其进行等距离多角度的观测,以探究高温目标的方向性;由于一台光谱仪无法同时获取多角度的观测数据,且不同角度观测时,高温目标温度发生明显改变,提出一种降温模型计算多角度观测的参比辐射亮度L0和辐射亮度比LR(多角度辐射亮度Lθ/参比辐射亮度L0),用以抵消高温目标降温的影响。高温目标辐射的方向性研究对于提高高温目标温度反演精度以及探究热辐射方向性的物理机制具有重要意义。
1 原理与方法
1.1 实验观测原理
由于高温目标辐射亮度较大,全视场观测会超出光谱仪能量阈值,所以采用非全视场对高温目标进行观测,但探测视场角度和观测视场在改变,需要由光谱仪读数推导出高温目标的实际辐射亮度,即建立多角度观测物理模型。

图1 多角度观测示意图Fig.1 Multi-angle observation diagram
多角度观测示意图如图1所示,记小面元高温目标在θ方向上的辐射亮度为L1,常温背景在θ方向上的辐射亮度为L2,光谱仪读数为L′,光谱仪半视场角为β,β=12.5°,ΔΩ为竹炭对光谱仪探头所张立体角,ΔΩ′为光谱仪视场角对应的立体角,观测半径为h,h=1.49 m,ΔS为高温目标上表面面积,ΔA为光谱仪探头入瞳处面积,光谱仪探头入瞳处接收辐射通量E等于高温目标与常温背景在光谱仪探头处的辐射通量E1与E2之和,
E1=L1·cosθ·ΔS·ΔΩ=L1·cosθ·ΔS·ΔA/h2
(1)
假设常温背景为朗伯体,当光谱仪垂直观测时,则其在光谱仪入瞳处产生的能量贡献为:全视场内朗伯扩展源在光谱仪入瞳处的能量贡献去除视场中心与高温目标同等面积的常温背景在光谱仪入瞳处的能量贡献:
E2=π·L2·ΔA·sin2θ-L2·cosθ·ΔS·ΔA/h2
(2)
E=E1+E2
=π·L2·ΔA·sin2θ+(L1-L2)·cosθ·ΔS·ΔA/h2
(3)
由于实验中竹炭温度>400℃,常温背景温度<20℃,取高温目标温度为673 K,常温背景温度为300 K,带入普朗克函数中,得到二者的辐射亮度值,当波长处于1350~2 500 nm之间时,L1>40 000·L2恒成立, 且L2最大值为5.984×10-6,趋于0,则
E=L1·cosθ·ΔS·ΔA/h2
(4)
由于倾斜观测要低于垂直观测的常温地物的辐射能量,因此上式依旧成立。又由光谱仪读数与接收能量的关系为:
E=L′·ΔA·ΔΩ′=L′·ΔA·2π·(1-cosβ)
(5)
得到光谱仪读数与高温目标在该方向上的辐射亮度的关系式,简称为角度较正式:
L1=L′·2π·(1-cosβ)·h2/(ΔS·cosθ)
(6)
1.2 降温模型
由于一台光谱仪无法同时获取多角度的观测数据,且不同角度观测时,高温目标温度发生明显改变,一组多角度观测需12~15 min,因此降温模型的研究是不可或缺的。研究发现,短波红外波长范围内的辐射亮度随时间变化可以进行高精度的曲线拟合,且该拟合形式对于此类高温目标(燃烧机制竹炭)具有普适性。
为确定多角度观测时曲线拟合得到零度数据的准确性,设计25~30 min时间跨度的高温目标自然降温实验,零度天顶角对其辐射亮度进行观测。实验共测量600个时间点的辐射亮度,选取点号为1~200和401~600的时间数据和辐射亮度数据作曲线拟合,计算该函数在201~400个时间点的辐射亮度值,认为光谱仪观测值为真值,以绝对误差及相对误差来判断该方案的可行性。
对600个数据点作L=f(t)=a1·exp(b1·t)+a2·exp(b2·t)形式的曲线拟合(图2),黑色线为拟合曲线。曲线拟合的确定系数为0.997 5,均方根误差为0.015 53。对选取的400个数据点作相同形式的曲线拟合,确定系数为0.997 7,均方根误差为0.017 9。图3为降温模型下的精度图,可以发现绝对误差及相对误差均较小,在一定精度内该方案可行。
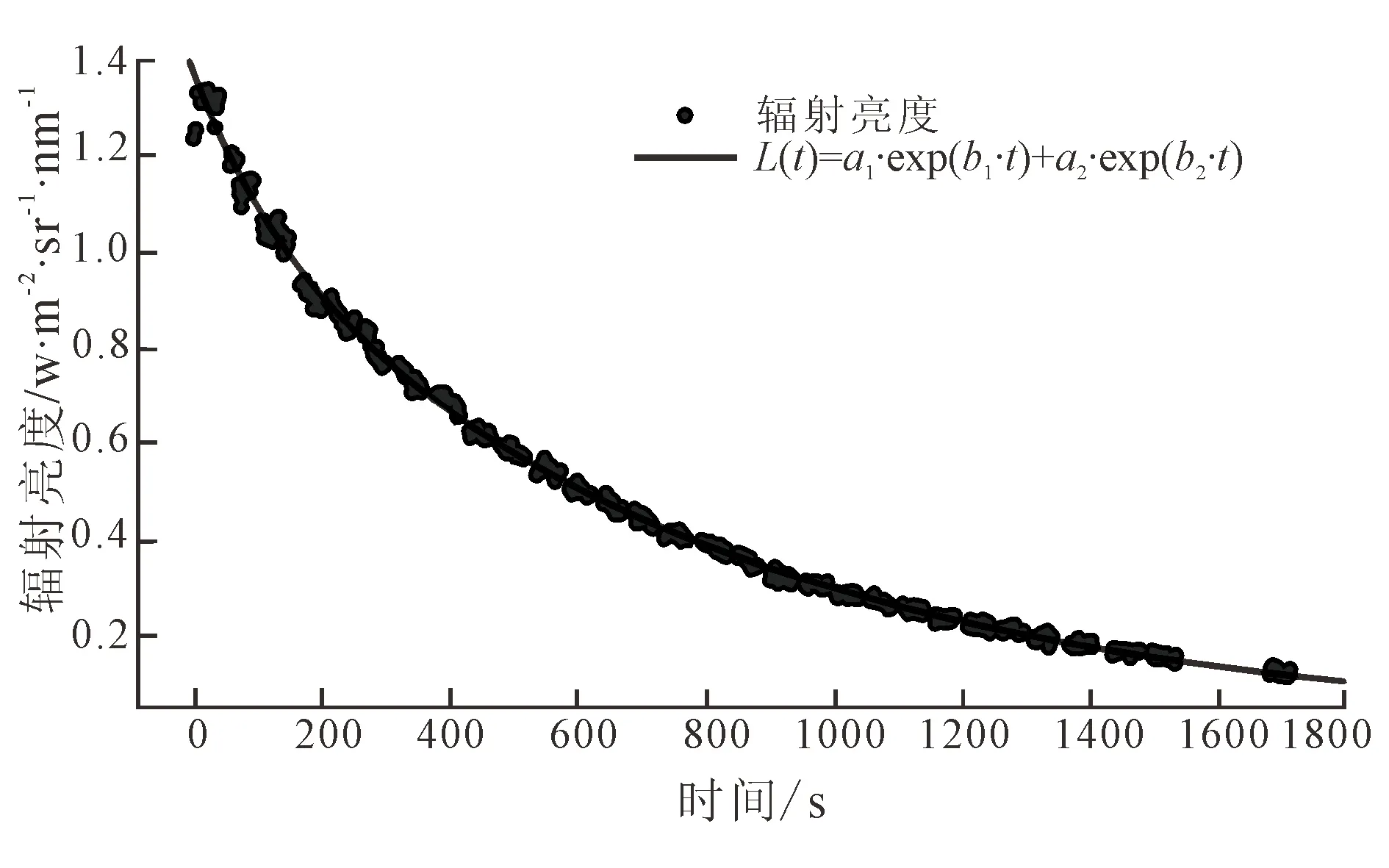
图2 降温模型Fig.2 Cooling model

图3 降温模型精度Fig.3 Cooling model accuracy
1.3 观测方案设计

图4 观测方案Fig.4 Observation plan
由于降温模型有很高的精度,构想出零度、多角度、零度天顶角交替观测的多角度观测方案(图4)。以t0-t1和t2-t3时间段内的零度天顶角观测光谱数据与时间数据作曲线拟合,得到辐射亮度随时间变化的模型,计算该曲线在t1-t2时间段内多角度观测时的取值,作为多角度观测时零度天顶角观测的参比辐射亮度,多角度亮度与参比辐射亮度数据作比,将亮度比随角度的展布作为辐射亮度的角分布。
2 实验观测
2.1 高温目标材料
使用形状规则的机制竹炭作为原材料,此种竹炭密度大,孔隙度小,耐烧。将竹炭制成表面平整,表面边长为4 cm的正方形,高为2 cm的长方体。以棱长为4 cm的无上盖的立方体小火炉作为容器,火炉2 cm高处固定有带小孔的炉底,以保证通风。竹炭放入火炉完全充填其表面,以保证高温目标的表面平整,形状规则,面积一致。
2.2 仪器简介及参数设置
ASD野外光谱分析仪FieldSpec 3是一种测量可见光到近红外波段(350~2 500 nm)地物波谱的便携式工具,能快速扫描地物,光线探头能在毫秒内得到地物单一光谱。光谱仪内有三个传感器,一个波长范围为350~1 100 nm 的VIR传感器和两个波长范围分别为1 000~1 900 nm和1 700~2 500 nm的SWIR1和SWIR2传感器,不同传感器之间工作状态有所差异,测量辐射亮度需要使用绝对测量方法,根据ASD光谱仪的定标说明,工作90 min后的SWIR1工作状态最为稳定,采用抛物线平滑的方式对VIR和SWIR2进行修正。因此,对于此实验,预热至少90 min和抛物线平滑必不可少。
实验采用裸光纤光谱仪进行测量,视场角为25°;每条光谱曲线为积分3次的平均值;每次积分138 ms;采集暗电流100次。原因为小面元高温目标的辐射亮度较小,选择较长的积分时间和较大的暗电流采集次数以增加信噪比,积分次数较少的目的是保证在单个角度测量过程中竹炭温度基本保持不变。
2.3 多角度观测方案
常温、无风、暗室条件下,光谱仪探头距离竹炭等距,距离设置为1.49 m,在同一方位角以不同天顶角进行观测。 方案具体为: 0°天顶角观测150次,需4 min;多角度观测,观测天顶角为0°~70°,以1°~2°为间隔,顺次增大,直至70°,每观测一次,记录一次观测角度,以度为单位,读数精确到小数点后一位,如此观测一组数据需要4 min±;0°天顶角观测150次。
2.4 数据处理
观测物理量为辐射亮度,多角度观测竹炭样品为26块,降温模型竹炭样品为26块,对获得原始辐射亮度数据进行抛物线平滑处理,将光谱仪记录数据通过角度校正式校正为地物真实的辐射亮度Lθ,利用降温模型计算出多角度观测时的参比辐射亮度L0,计算辐射亮度比LR。
3 结果
由于辐射亮度也为波长的函数,每50 nm波长间隔取辐射亮度,作其与时间的散点图和上述指数形式的拟合(图5),蓝色点为小面元高温目标在0°的辐射亮度,黑色点为其在0°~70°的辐射亮度,红色线为上述指数形式的拟合。从散点图及拟合效果可知,当波长λ∈[350 nm,1 350 nm],小面元高温目标在0°的辐射亮度与多角度辐射亮度数据信噪比均较低,无法说明其差异;当波长λ∈[1 400 nm,2 500 nm],随着波长的增加,数据信噪比逐渐增加,零度亮度数据采用指数形式拟合的精度逐渐提升,且多角度亮度数据与零度亮度数据差异越来越明显。
实验过程中,小面元高温目标的最高温度在800 K±,根据维恩位移定律知辐射的峰值波长在3 600 nm附近,ASD光谱仪虽不能获取峰值波长附近的数据,但在1 600~2 500 nm仍有较好的响应,探测器波长范围内,波长越大,数据对温度越敏感,信噪比也越大。从应用角度出发兼顾在1 950 nm和2 450 nm附近有两个水汽吸收带,所以选择Landsat8 SWIR2的标称波长附近为研究波长,对2 200 nm波长的辐射亮度数据进行初步研究。采用L=f(t)=a1·exp(b1·t)+a2·exp(b2·t)形式对26个样品在2 200 nm的辐射亮度与时间数据进行拟合(表1),均方差(RMSE)均<0.035,确定系数(R-Square)均>0.97,说明拟合精度很高,但拟合系数并无规律。
由于不同样品观测的初始温度不同,辐射亮度也不同,辐射亮度比这一概念可以将不同样品“归一化”,使不同样品具有可比性。辐射亮度比随角度变化规律在不同波长的适用性也应该考虑,考虑不同样品的差异特征,仍以50 nm为间隔,对不同波长的数据以傅里叶级数形式作曲线拟合(图6),其中蓝色点为某一样品在该波长的亮度比数据,红色线为此样品在该波长的傅里叶级数拟合曲线。得到与辐射亮度-时间拟合相似的规律:波长λ∈[350 nm,1 350 nm]亮度比数据信噪比均较低无明显规律;波长λ∈[1 400 nm,2 500 nm]的数据信噪比逐渐增加,拟合效果大体随波长增大而提升。

笔者也对所有样品在波长为2 200 nm处辐射亮度比与角度采用的拟合方式进行了研究,得到三角函数形式拟合曲线系列(图7),多项式拟合系列及傅里叶级数拟合(图8)。拟合精度如表2所示,结果表明随着拟合参数的增加,拟合精度在逐渐增加,4个参数的拟合确定系数都达到了0.987,本文主要研究了小面元高温目标在0°~70°天顶角的辐射亮度变化,笔者观测了90°天顶角的辐射亮度,发现其与0°~70°的数值相差四个数量级,而四个参数的拟合均存在“翘尾巴”的现象,说明此三种拟合均为过拟合,而三参数的两种拟合均不存在过拟合现象,但拟合系数的物理意义尚不知晓。
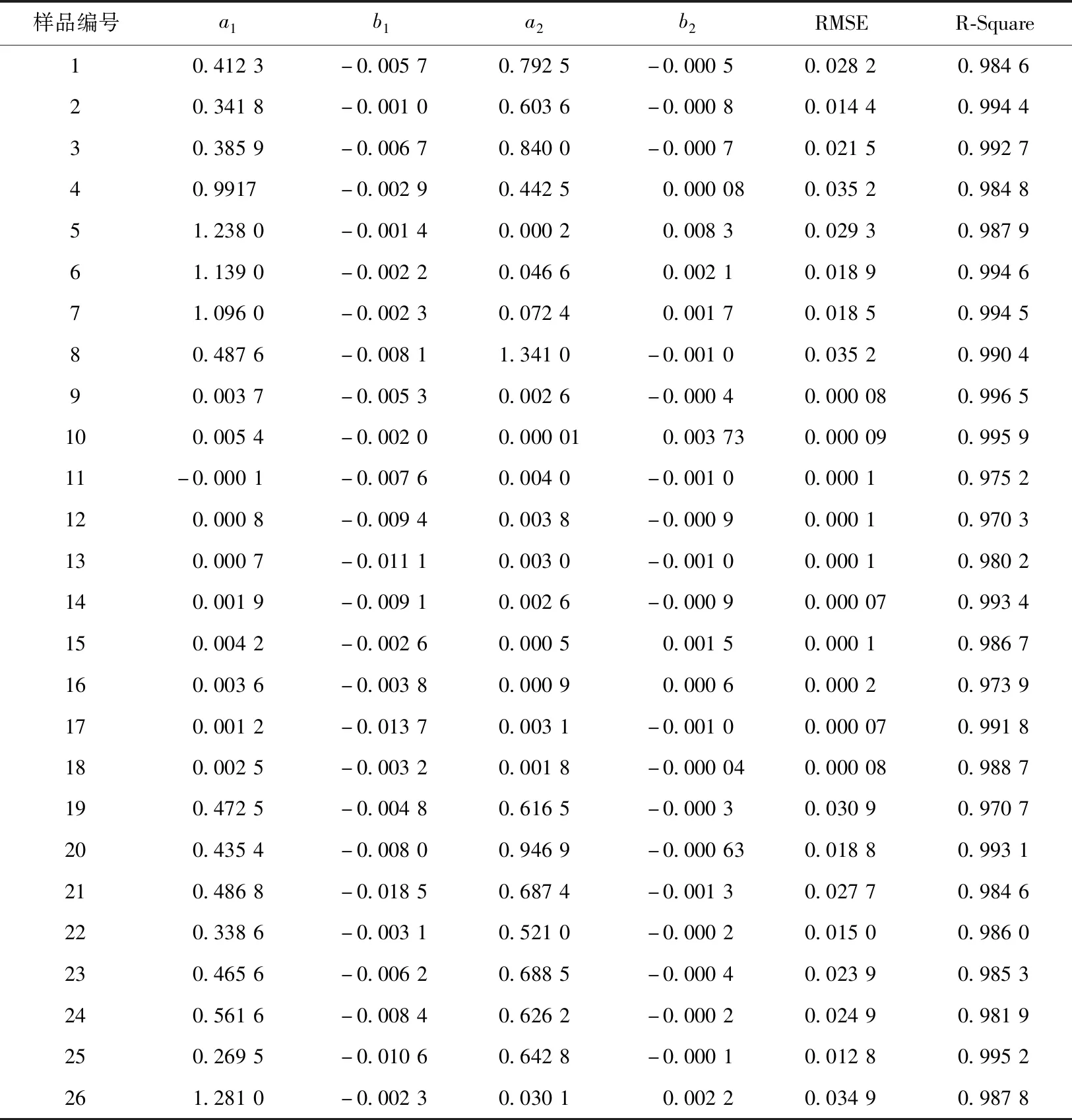
表1 拟合参数

表2 拟合精度对比
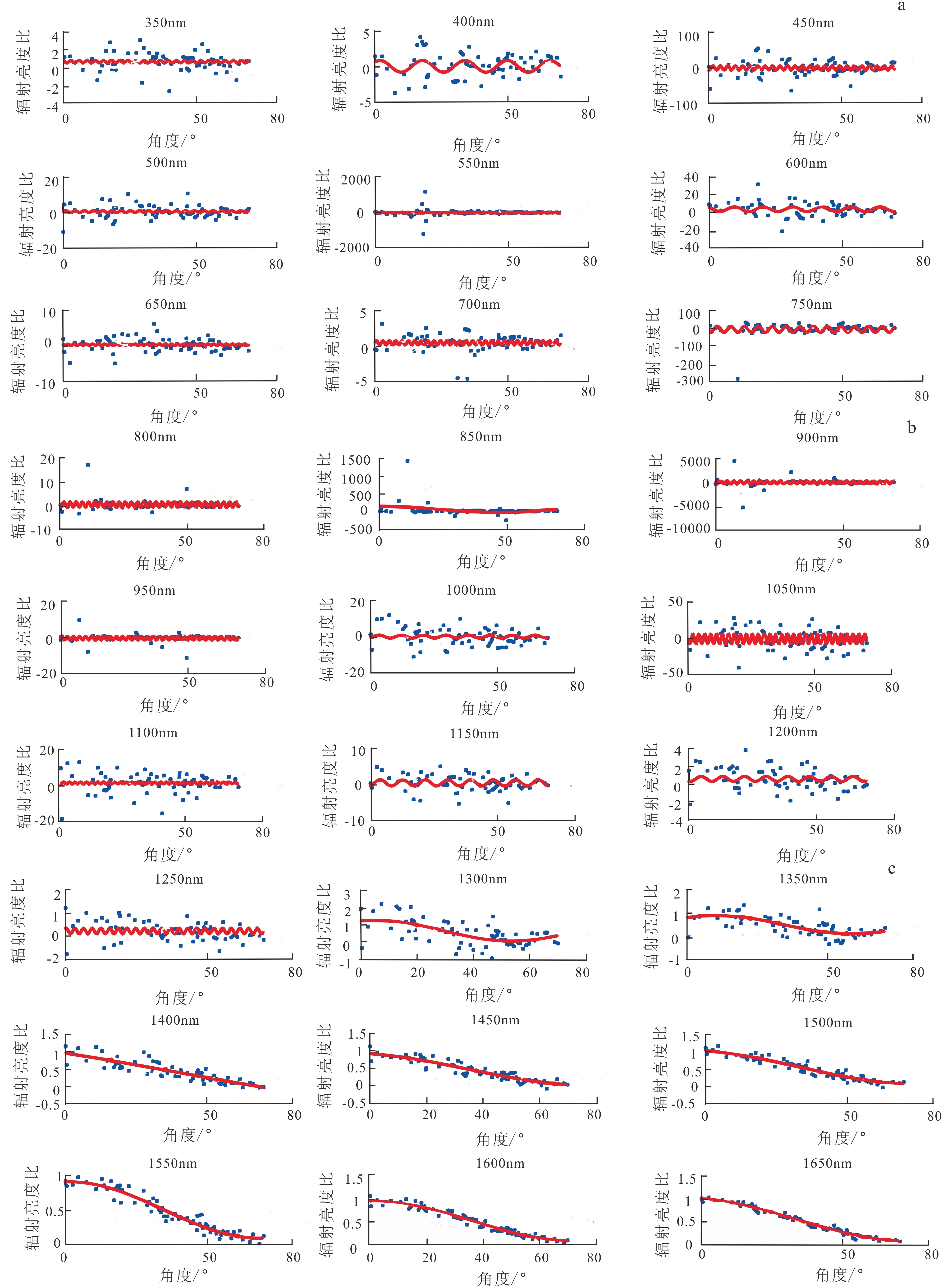

a.波长范围1; b.波长范围2; c.波长范围3; d.波长范围4; e.波长范围5.图6 不同波长的辐射亮度比拟合Fig.6 Radiation ratio fitting of different wavelengths

图7 三角函数表达式拟合Fig.7 Trigonometric function expression fitting

图8 多项式形式拟合Fig.8 Polynomial fitting
4 结论
(1)以燃烧机制竹炭为小面元高温目标在端元尺度下的短波红外波长范围具有显著的方向性。
(2)小面元高温目标在端元尺度下的短波红外波长范围的方向性可以用辐射亮度比这一概念刻画。
(3)余弦函数、多项式、傅里叶级数均可实现对辐射亮度比随角度变化的高精度拟合。
(4)区别于常温地物观测前后时间差里无规则的地表热平衡变化,高温目标的辐射亮度变化符合二重指数形式的降温模型,依据降温模型的零度-多角度-零度交替观测方案巧妙地消除了时间差“噪声”。
——多功能光谱仪

