倾斜台阶重力异常正演计算公式剖析
马国庆,李宗睿,李丽丽
吉林大学 地球探测科学与技术学院,长春 130026
0 引言
倾斜台阶可用于模拟实际地层的断裂、接触带等,利用其重力正演公式可获得断裂等相似地质体的重力异常特征,从而为数据解释提供依据。对于台阶正演结果的反演可模拟对于断裂等相关地质体的反演,从而对反演的可靠性进行评估;在一些需要迭代计算的反演中还需要正演公式参与运算。因此准确的台阶公式至关重要。
倾斜台阶的重力异常表达式在国内外众多教材及文章[1-8]中出现并应用。很多断裂特征反演的方法[9-11]大多是通过台阶正演计算公式来进行推导,因此重力异常正演公式的正确性至关重要。
对现有教材及论文中正演公式进行模型试验表明,在一定条件下倾斜台阶的重力异常曲线会出现不规则的畸变。冯兰天[12]和苏和朋等[13]也通过模型正演证明了台阶重力异常计算公式所存在的畸值问题,但其未针对产生畸值的条件进行分析,且在公式推导中存在一定的错误。
笔者对现有的正演计算公式及结果展开分析,明确了现有公式产生畸值的原因及条件,并基于台阶的正演计算积分展开式,推导获得了新的台阶重力异常正演计算公式。模型试验表明重新推导公式所获得数据不存在畸点,且发现原有公式是由于在合并中未考虑反三角函数值域而出现的误差。
1 倾斜台阶重力异常间断点的出现
以水平方向为x轴,垂直方向为y轴,建立坐标系,绘制倾斜台阶模型(图1)。
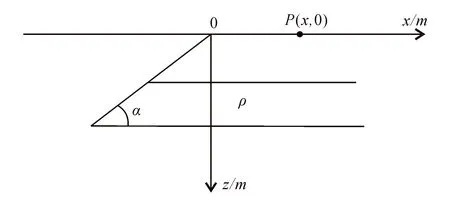
图1 倾斜台阶模型Fig.1 Tilt step model
在图1所示情况下,倾斜台阶常规计算公式为:
(1)
式(1)中,G为万有引力常数;ρ为场源与围岩之间的密度差;x为地面上观测点的坐标;h为倾斜台阶上顶面的埋深;H为台阶下底面的埋深;α为台阶的倾斜角。
根据式(1),设倾斜台阶模型参数为:h=10 m,H=100 m,倾角分别取45°、60°、90°、120°、135°,场源与围岩之间的密度差异设置为1 000 kg/m3,万有引力常数设为6.670 8×10-11m3kg-1s-2,根据式(1)得到不同倾角的倾斜台阶重力异常曲线(图2)。

图2 倾斜台阶模型重力异常曲线(α=45°、60°、90°、120°、135°)Fig.2 Gravity anomaly curve of tilt step model
从图2中可以看到在倾角为60°、90°、120°时使用该公式,重力异常曲线并未产生畸变。因此并非所有情况下使用该公式都会产生畸变。为进一步进行分析,保持其余参数不变倾角分别取30°、45°、135°、150°,得到相应的重力异常曲线(图3)。

图3 倾斜台阶模型重力异常曲线(α=30°、45°、135°、150°)Fig.3 Gravity anomaly curve of tilt step model
为研究畸点产生的原因,针对式(1)进行分析。
由于该公式项数过多,不便于整体分析,所以考虑逐项讨论其连续性。又因为常数项不影响函数的连续性,因此仅对含自变量的项进行分析。
令:
(2)
(3)
(4)
(5)
则:
Δg=GΔρ[π(H-h)+f1-f2+f3-f4]
(6)
显然分析Δg的连续性可转化为分析f1,f2,f3,f4的连续性。
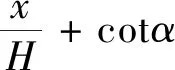




(7)
2 倾斜台阶异常公式的推导
为解决畸变问题,对倾斜台阶重力异常公式重新进行推导。
引力场F是保守场(沿闭合路线做功为0)或无旋场,考虑到标量函数梯度的旋度恒等于零,可引入引力位V(标量函数):

(8)
式(8)说明引力的方向始终指向引力位增加最快的方向。
对于质量为m的质点引力场外,某点的引力位的定义为:将单位质量的质点从无穷远移至该点时引力场所做的功,即

(9)
质体外的引力位为:
(10)
对于二度体来说(所谓的二度体就是横截面的形状和深度沿某一水平方向不变且该方向无限延伸的物体),以地面上某一点O为坐标原点,z轴铅直向下即沿重力方向建立笛卡尔坐标系。若物体的剩余密度均匀,则二度体的重力异常可表示为:

(11)
在图1所示模型下,台阶在x轴上任意一点P(x,0)的重力异常应为:
(12)
得出重力异常的表达式,需要解此定积分,详细过程为:

(13)
带入到重力异常表达式(12)中有:
(14)
对于式(14)中积分的前一项:
(15)
(16)

(17)
运用分部积分法,则有:
(18)
(19)
则有:At2+Bt-Atcotα-Bcotα+ct2+c=x,得到:

(20)
解得:

(21)
因此有:
(22)
再带入到原来的重力异常表达式(14)中得:
(23)
对比传统的倾斜台阶重力正演公式,由于:
(24)
其中:a,b∈R,c为整数。
传统公式实际上是对新公式后两项进行合并后的结果,而合并时未考虑c,因此产生了间断点。传统的倾斜台阶重力异常公式本身并没有错误,只是需要在合并时对c进行分析。
由反正切函数性质可知:

(25)
则:
arctan(a)+arctan(b)∈(-π,π)
(26)

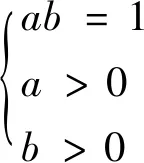
(27)
又由于:
(28)
因此:
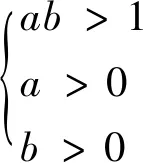
(29)
即:
(30)
同理可得:

(31)

(32)
且证:

(33)

(34)
综上所述:
arctan(a)+arctan(b)
(35)
因此,若要传统公式(1)与新公式(23)等价可将其写为:
(36)
式(36)中u=x(H-h)sin2α,v=x2sin2α+(H+h)xsinαcosα+Hh。
3 模型试验
运用新推导的倾斜台阶重力异常公式(23)以及加入判定条件后的传统公式(36)分别用Mathematics进行正演计算。使用相同的参数,即设倾斜台阶模型参数为:h=10 m,H=100 m,倾角分别取15°、45°、90°、135°、165°,场源与围岩之间的密度差异设置为1 000 kg/m3,万有引力常数设为6.670 8×10-11m3kg-1s-2,分别得到图4、图5。

图4 新倾斜台阶重力异常公式得到的重力异常曲线Fig.4 Gravity anomaly curve obtained by new formula of gravity anomaly of inclined steps

图5 加入限定条件后传统台阶重力异常公式得到的重力异常曲线Fig.5 Gravity anomaly curve obtained by traditional step gravity anomaly formula after adding qualified conditions
从图4可以看出新推导出的倾斜台阶重力异常公式是正确的。而图5得到了与图4完全相同的结果,因此传统倾斜台阶重力异常公式在加入适当的限定条件后同样正确。且当倾角为任意值时,曲线均是连续的,有效地解决了以往公式中出现的畸变问题。
4 结论
(1)现有倾斜台阶的重力正演公式由于在推导过程中未考虑反三角函数的值域变化造成了畸点的出现。
(2)从台阶重力异常积分公式出发,对倾斜台阶重力异常正演公式重新进行了正确的推导,模型试验表明新推导公式有效地避免了畸点的产生。

