基于Stearns-Noechel模型的色纺纱配色算法改进

马崇启，朱宝基，刘凤坤，买 巍，刘建勇

（1.天津工业大学纺织科学与工程学院，天津300387；2.中国纺织信息中心综合业务部，北京100125）

色纺纱，就是将纤维先染成有色纤维，然后将两种或2种以上的有色纤维进行混纺，得到具有独特混色效果的纱线[1-2]。色纺纱与本色纤维纺纱相比，在生产过程中存在一些困难之处，最重要的就是配色难的问题[3]。目前的色纺企业在打样时，更多的是依赖人工配色，配色人员根据经验对客户来样进行配方分析后纺制小样，然后再不断修正小样，直至符合要求[4]。人工配色所需的工作量较大，耗时较长，且配色结果容易受天气、配色人员情绪等因素影响，配色准确率低[5-6]。随着计算机行业的快速发展，利用计算机进行配色成为色纺纱发展的一种必然趋势[7]。

Stearns-Noechel模型作为色纺纱计算机配色的代表性模型之一，有较多学者对其进行研究。陈维国等[8]对Stearns-Noechel模型中的参数进行修正，并提出一种羊毛混色纺纱计算机智能测色配料系统；王春燕[9]使用Stearns-Noechel模型预测纬全显色提花织物颜色的色差，并得出实验材料为真丝时该模型的参数值；韩瑞叶等[10]基于Stearns-Noechel模型对数码转杯纺的配色规律进行研究，通过优化模型参数，降低配色的平均色差。上述文献中，模型参数主要通过实验进行确定与优化，配色的平均色差虽得到降低却不能保证小于1，而且不同纤维的M值不同，一个固定的参数值并不一定适用于所有色纺纱的配方预测。鉴于此，本文通过Matlab对Stearns-Noechel模型中参数M的确定方法进行改进，并在此基础上提出结合人眼视觉特性进行色纺纱配色的假设，以提高色纺纱配色的准确性。

1 实验部分

1.1 实验材料及仪器

材料：涤纶纤维，包括大红色、旦黄色、宝石蓝色、紫罗兰色、桔红色、茵绿色6种，纤维长度为38 mm，线密度为1.56 dtex，滁州安兴环保彩纤有限公司产品。

仪器：XFH型小型和毛机，青岛市胶南针织机械厂产品；小型数字式梳棉机、小型数字式并条机、小型数字式粗纱机和小型数字式细纱机，天津市嘉诚机电设备公司产品；Y381A型摇黑板机，常州第二纺织机械厂产品；SF600 Plus型分光光度仪，美国Datacolor公司产品。

1.2 实验样品制备

将一次色大红色、旦黄色、宝石蓝色和二次色紫罗兰色、桔红色、茵绿色的纤维分别按照一定的比例进行三色混纺，得到57个混色样，分别求解每个混色样的最佳参数M值。随机选择20种不同比例的三色混样预测配方，混色样比例如表1所示。

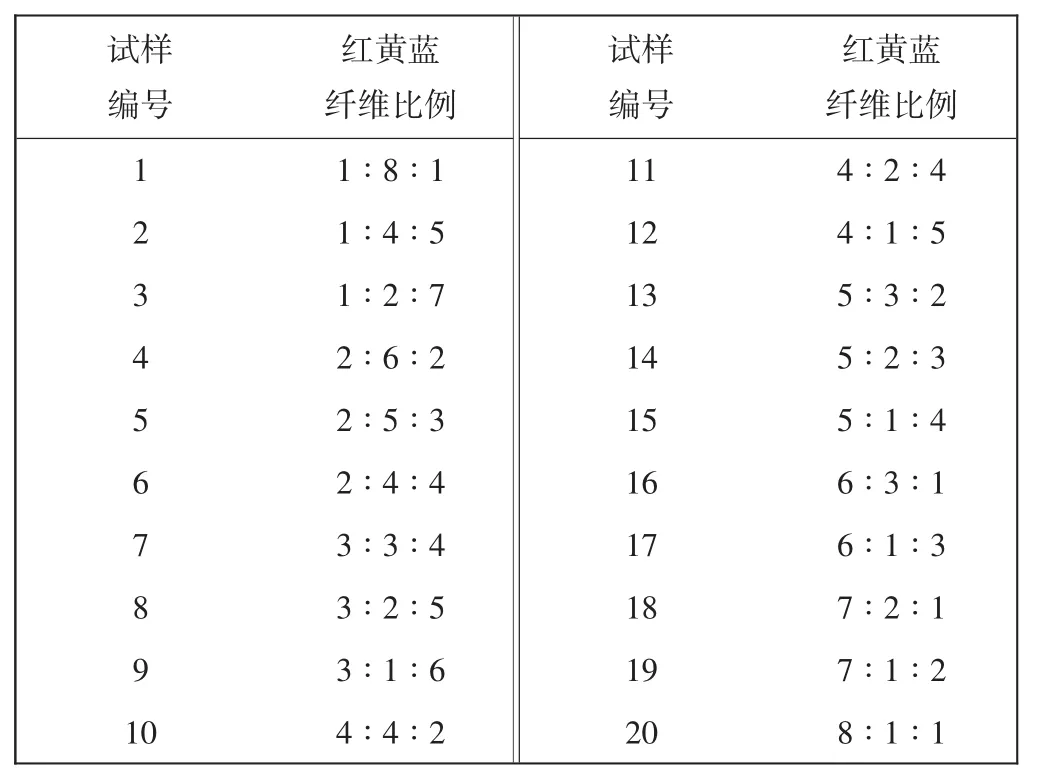
表1 混色纤维质量比Tab.1 Proportion of blended fibers

1.3 测试方法

本试验采用SF600 Plus分光光度仪进行测试。仪器进行预热和校正后，在D65标准光源下对样品测色，为了全面反映测色材料的颜色特征，使测色结果相对准确，测量时选择大孔径（30 mm）[11]。对每个样品在不同位置测量10次，取平均值，记录每个样品在可见光谱400～700 nm时的反射率值，间隔设置为10 nm。测色过程中，应确保每次测量得到的色度学参数之间的偏差小于0.1，若偏差较大，适当增加测量次数。

2 最优参数值预测配方

2.1 Stearns-Noechel模型

不同颜色的单色纤维混合纺制成混色样，这个过程属于物理混合，所以可以假设存在一个关于反射率的中间函数f[R（λ）]，使得混色后的纤维与组成它的单色纤维有如下关系[12]：

式中：Rblend（λ）指混色纤维在波长为λ时的反射率；Ri（λ）为组成混色纤维的单色纤维在波长为λ时的反射率；xi为组成混色纤维的单色纤维的质量比，且xi需要满足式（2）：

1944年，Stearns和Noechel在公式（1）的基础上，通过大量的实验，提出了一个关于反射率的中间函数f[R（λ）]的经验公式，称之为Stearns-Noechel模型[13]：

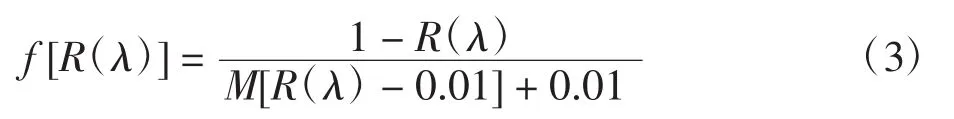
式中：M为可变参数；R（λ）为波长为λ时的反射率。已有许多学者对不同纤维的M值进行了研究，如表2所示。

表2 Stearns-Noechel模型中不同纤维的M值Tab.2 M value of different fibers in Stearns-Noechel model

本文对57个混色样各自达到最小匹配色差时的M值进行求解，去除因实验操作误差等原因产生的异常值，求解剩余混色样平均色差达到最小值时的M值，即为模型的最优参数，结果为0.184 2。结合上述公式和最优参数，可计算拟合配方。

2.2 拟合配方的计算

本文所研究的为三色混纺，由式（1）可知，3种不同颜色的纤维进行混纺后得到的混色纱线与这3种单色纤维的关系可以用公式表示，具体如下：

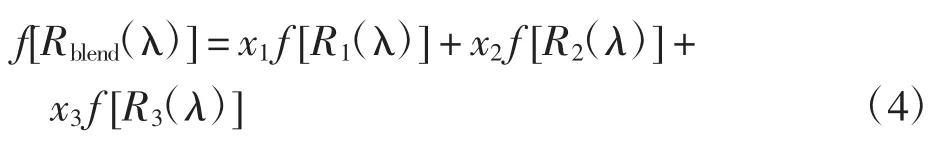
本文所用的配色方法为基于最小二乘法的反射光谱匹配，其本质是使拟合样与标准样在不同波长时的反射率差值尽量达到最小，即其中是波长为λ时标准样s的反射率；Rm是波长为λ时拟合λ样m的反射率。

选择可见光波长400～700nm进行配色，每隔10nm记录一次反射率，一共可以得到31个反射率值。拟合配方的具体计算过程为：纤维质量比X=[x1x2x3]T，单色纤维关于反射率的中间函数可构成矩阵

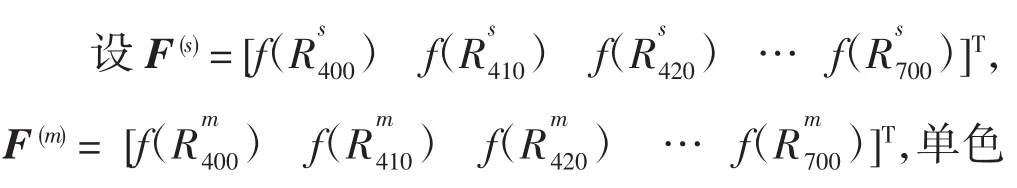
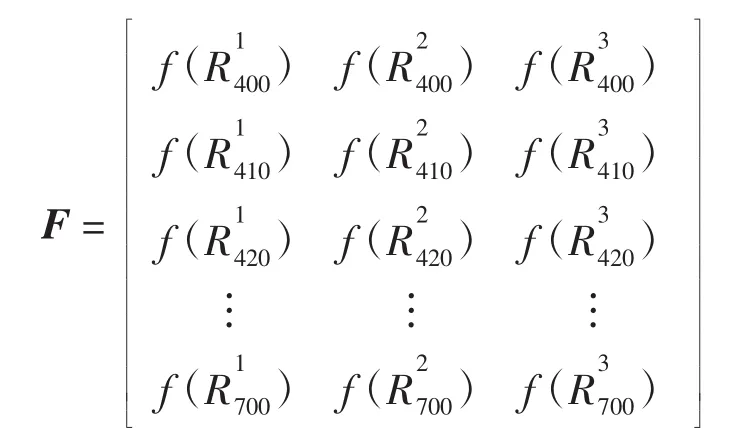
考虑到计算出来的初始配方可能出现x1+x2+x3不一定等于100%的情况，但实际生产计算中配比之和需为100%，所以需对初始配方进行归一化处理，得到合理的拟合配方。

2.3 评价标准

本文通过CMC（l：c）色差公式计算标准样与拟合样之间的拟合色差，其中l=2，c=1。根据计算出的拟合色差大小，评价配色算法的准确性。正常情况下，色差小于0.2时，人眼无法区分出颜色的变化；色差介于0.3与0.6之间时，表示两者在颜色上有较小差异；色差介于0.7～1.2时，表示两者在颜色上有差异，但可以被接受；色差介于1.2～2.1时，表示两者在颜色上差异非常明显[20]。所以，色纺纱配色时，拟合色差越小，得到的预测配方越准确。

2.4 参数M固定预测配方

本实验选取20种不同比例的三色混样，计算最优参数固定时（即M=0.184 2）预测配方得到的拟合色差，结果如表3所示。

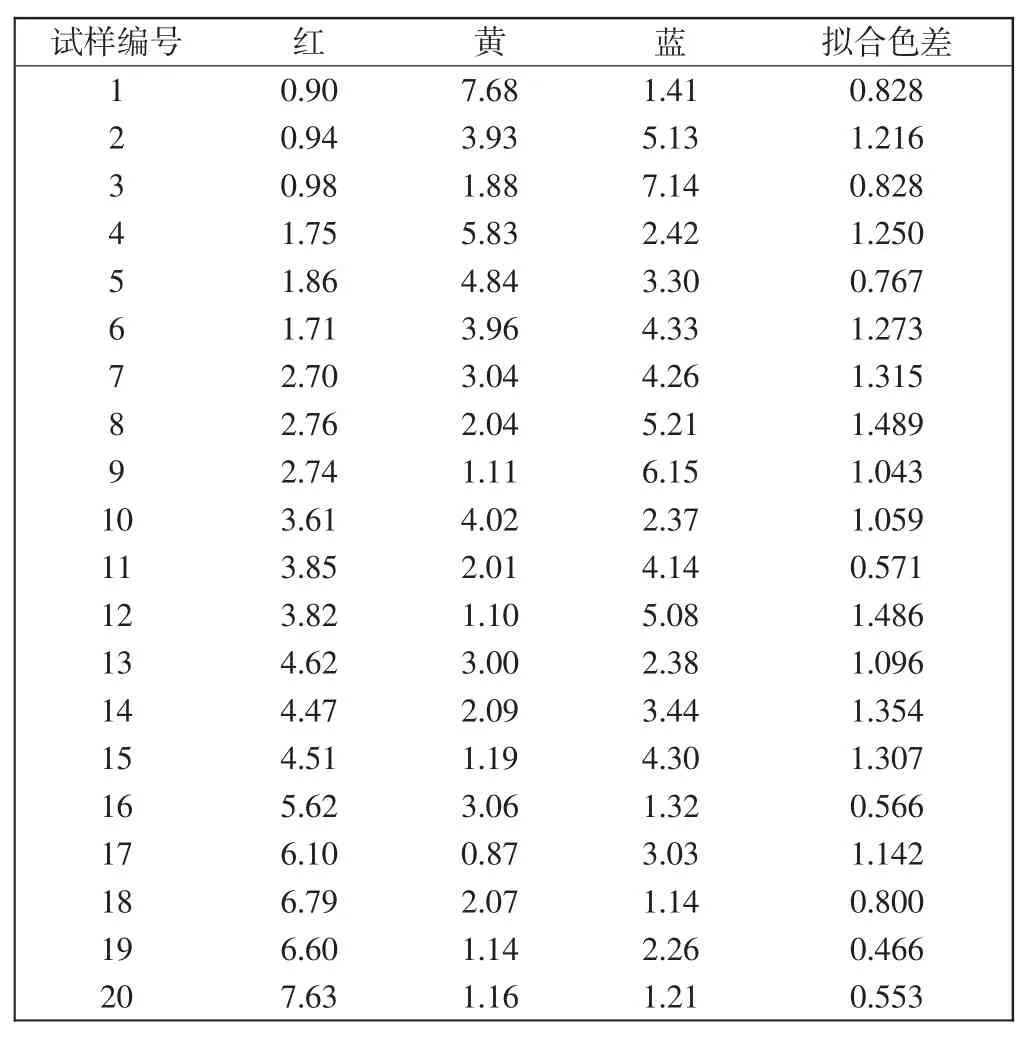
表3 参数固定时的拟合配方与拟合色差Tab.3 Fitting formula and fitting color difference when parameters are fixed

由表3可知，参数M固定时预测配方，所得到的平均拟合色差为1.02，配色结果相对较好。但实际上，不同比例的纤维混纺时的最优M值不同，将M值通过实验确定为0.184 2进行配色，其结果是存在误差的。对某混色样配色时，当固定的M值比较接近该试样的最优M值时，所得拟合配方较好，色差较小，反之若与该试样的最优M值相差较大，则拟合配方就会较差，色差相对较大。而且，采取固定最优参数进行配色，对色纺企业来说工作量较大，因为色纺并不是只用一种原料混纺，更多时候是不同的纤维进行混纺。考虑到这些因素，可通过改变参数M的确定方法去实现配色算法的改进。

3 配色算法的改进

3.1 参数M循环赋值预测配方

由上述可知，参数固定预测配方，工作量较大，其平均拟合色差大于1且存在一定的不准确性。所以本文通过对未知参数M进行循环赋值来预测配方。具体思路为：测色得到混色试样和组成混色样的单色纤维的反射率，在0.001～1的范围内每隔0.001对参数M进行循环赋值，并结合反射光谱匹配求出每个M值对应的拟合反射率，计算标准样与拟合样的色差，选择色差最小时的M值为最优参数，并输出最优参数对应的拟合配方与拟合色差。配色流程如图1所示。

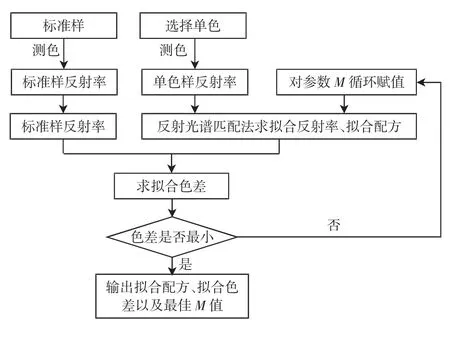
图1 参数循环赋值时的配色流程图Fig.1 Color matching flow chart when parameter loop assignment

根据图1的配色流程，本文就之前20组混色试样进行配色，计算出拟合配方、拟合色差。改进后的配色算法，最优参数可以直接得到，单色纤维质量比不同，得出的最优M值也不同，具体结果见表4。

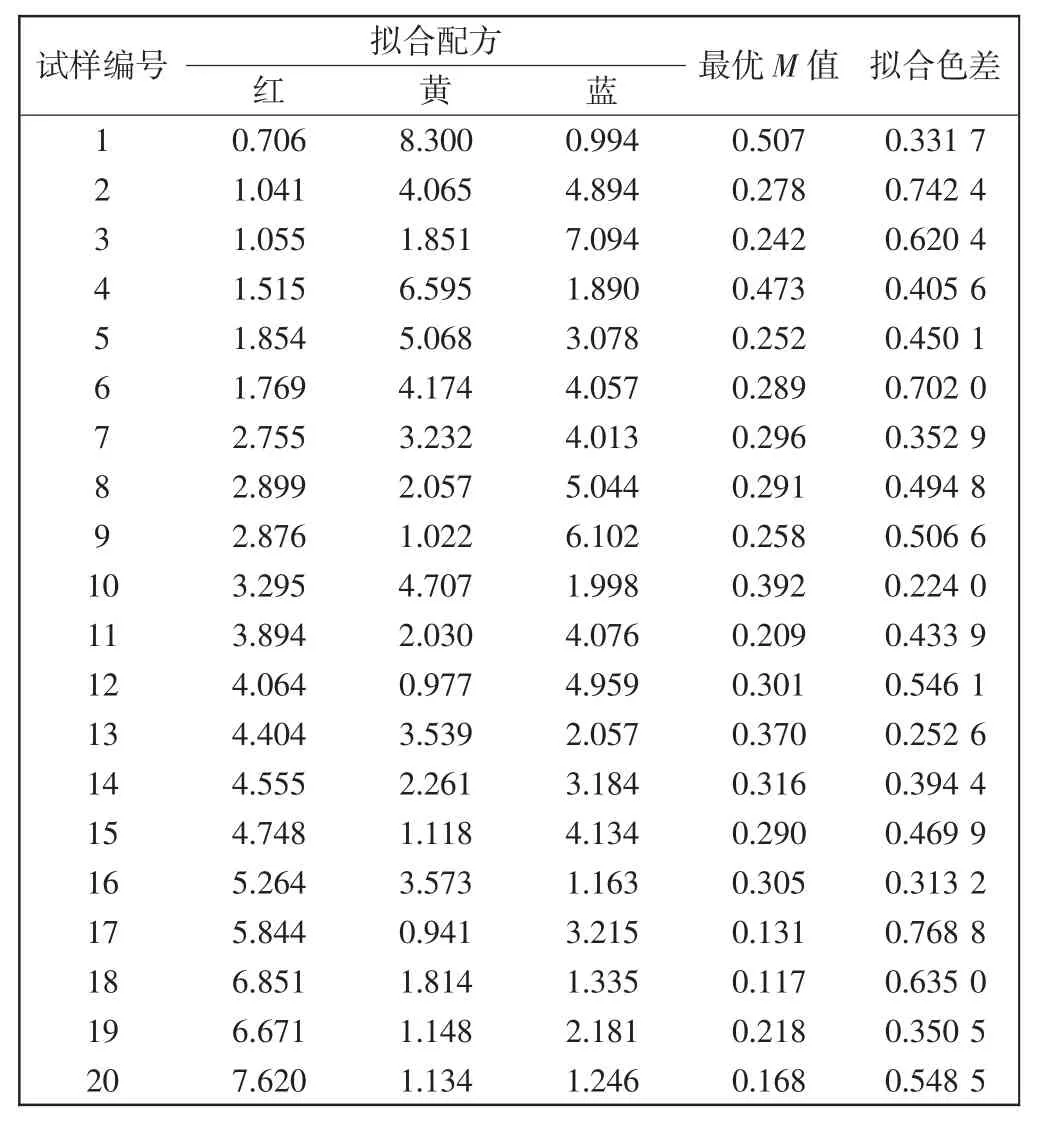
表4 参数循环赋值时的拟合配方与拟合色差Tab.4 Fitting formula and fitting color difference when parameter loop assignment

根据表4可知，参数M循环赋值时预测配方，拟合样与标准样之间的色差均小于1，计算得其平均拟合色差为0.477，比参数M固定时得到的拟合色差小，配色结果非常好。参数M循环赋值预测配方，不用进行大量实验去确定最优参数，而且对纤维类别没有限制，在减轻工作量的同时提高了配色的准确度。该配色算法的改进，提高了色纺纱配色时的生产效率，为后面的计算机配色研究奠定基础。

3.2 基于人眼视觉特性预测配方

由3.1可知，对参数循环赋值可以使标准样与拟合样的色差减小，本节在此基础上，对配色算法做进一步的改进。物体颜色的呈现离不开人的眼睛，在对物体颜色进行研究时，需要考虑到人眼视觉特性，即人眼的视觉神经对不同波长的光的感光灵敏度不一样[21]。为了使配色结果更准确，在对色纺纱配色时，也应将人眼的视觉特性考虑在内。所以假设人眼对于不同波长的反射率的敏感程度符合正态分布，将该假设在Matlab里用代码进行表示并用于配色，通过比较拟合色差大小看该假设是否适用于色纺纱的计算机配色，具体配色流程如图2所示。

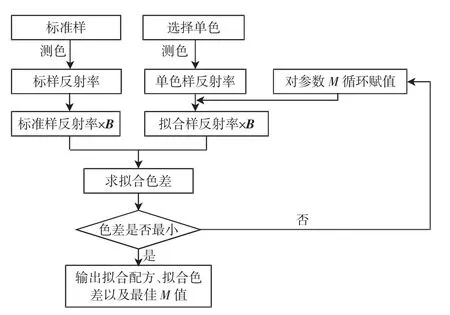
图2 基于人眼视觉特性时的配色流程图Fig.2 Color matching flow chart based on human visual characteristics

设定权值为50，number_QZ=50

建立一个50行31列的空矩阵，A=zeros（number_QZ，31）

建立一个求总和的数组，total=zeros（1，number_QZ）

For y=1：number_QZ

For x=1：31

A（y，x）=gaussmf（x，[y 16]）

End

End

For y=1：number_QZ

For x=1：31

total（1，y）=total（1，y）+A（y，x）

End

End

For y=1：number_QZ

For x=1：31

A（y，x）=A（y，x）/total（1，y）

End

End

B=A′

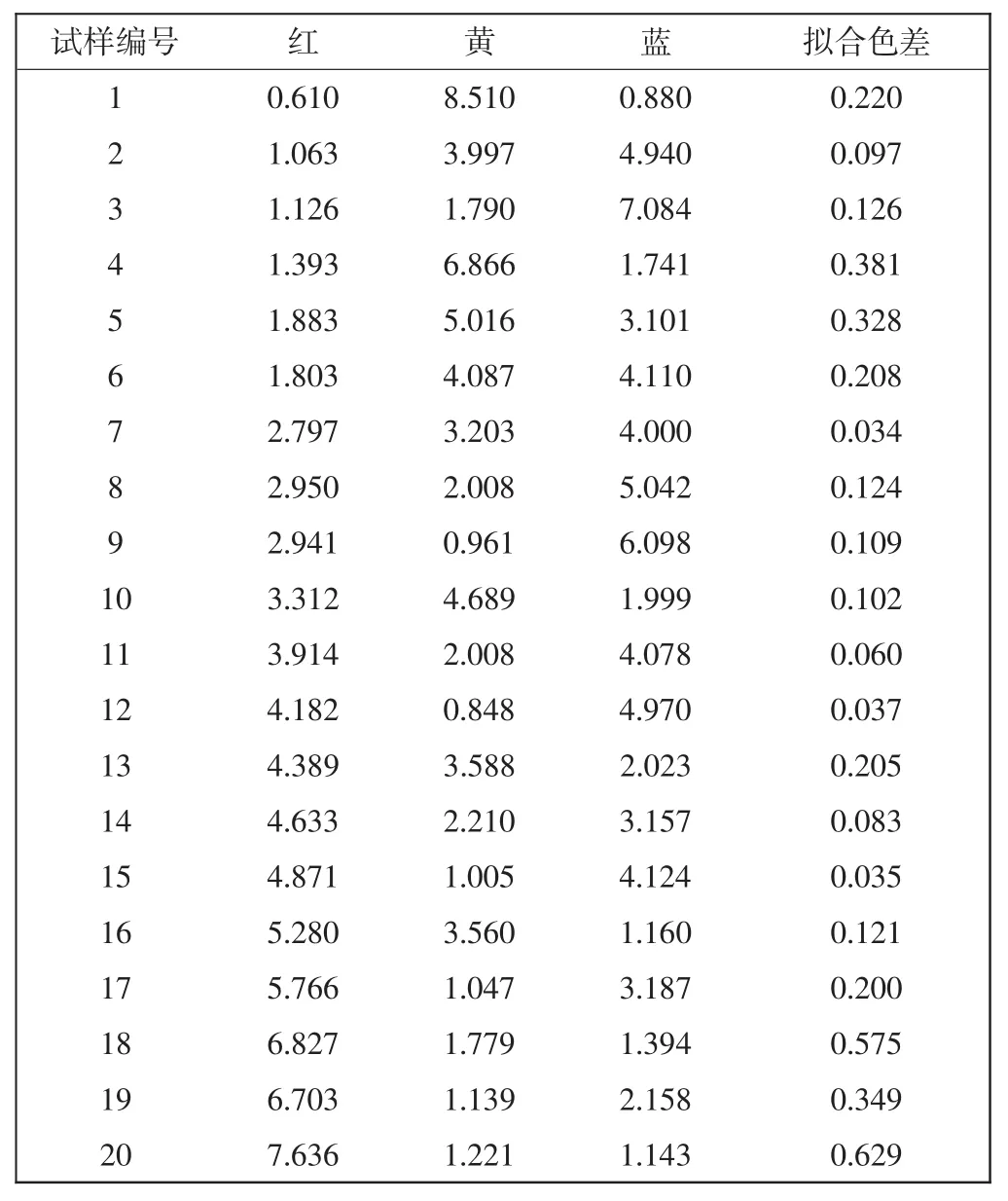
表5 考虑人眼视觉特性时的拟合配方与拟合色差Tab.5 Fitting formula and fitting color difference when considering human visual characteristics

根据表5可知，假设人眼对于不同波长的反射率的敏感程度呈正态分布，并在此基础上预测配方，得到的拟合样与标准样之间的色差均小于1，计算得其平均拟合色差为0.201，配色效果极好。本节的算法改进，在对参数M进行循环赋值的同时，对标准样和拟合样的反射率按照假设附加权值系数后进行配色，使配色准确度得到提高。所以，之前对于人眼视觉特性的假设可以成立，此配色算法的改进适用于色纺纱的计算机配色。

4 配色结果对比

上述预测配方的算法中，所用混色试样相同，所以可以对这3种配色算法得到的拟合色差做箱体图进行对比分析，这样可以更清楚地看出配色算法的改进效果。图3所示为配色算法改进前后拟合色差的对比。

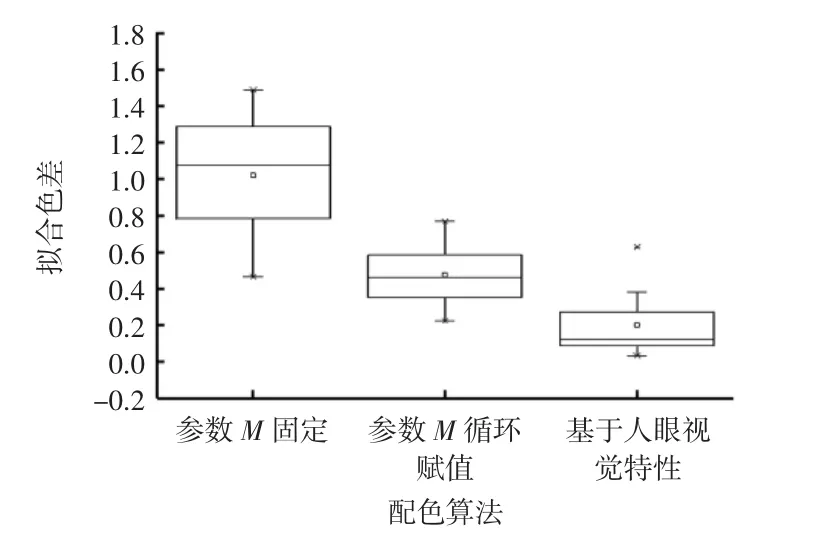
图3 配色算法改进前后对比Fig.3 Com parison of color matching algorithm s before and after im provement

由图3可以看出，对于相同的混色试样进行配色，随着配色算法的改进，配色准确度也得到提高。通过进行大量实验确定出最优参数进行配色，得到的平均拟合色差为1.02，中位数为1.08。对配色算法进行改进，使参数M在0.001到1的范围内循环赋值，选择色差最小时对应的M值进行配色，得到的平均拟合色差为0.48，中位数为0.46，配色准确率得到提高。在第一次改进的基础上，将人眼视觉特性考虑进来进行算法改进，配色效果得到进一步提高，其平均拟合色差为0.201，中位数为0.125。同时，由图5的箱体图也可以直观地看出配色算法改进后的配色效果，参数M值固定时的箱体较大，而参数M循环赋值时和基于人眼视觉特性时的箱体都较小，且整体的拟合色差都在1以内。

5 结论

本文以Stearns-Noechel模型为基础，经过实际打样计算出一个固定的参数M作为最优参数进行配色，平均拟合色差大于1且工作量大，文章就此问题对配色算法进行改进。第1次改进是对参数M进行循环赋值，选择色差最小时对应的M值为最优参数预测配方，平均拟合色差为0.477，中位数为0.46，小于0.5，配色效果得到提高。在此基础上，结合人眼视觉特性对配色算法进行第2次改进，平均拟合色差为0.201，中位数为0.125，小于0.3，配色效果得到进一步提高。所以，基于Stearns-Noechel模型改进后配色算法，可以应用于色纺纱的计算机配色。