电站锅炉SCR脱硝系统联合运行优化模型
李 伟,徐 强,孔德安,赵 翔,郜 宁,吕 游
电站锅炉SCR脱硝系统联合运行优化模型
李 伟1,徐 强1,孔德安1,赵 翔1,郜 宁2,吕 游3
(1.国网新疆电力有限公司电力科学研究院,新疆 乌鲁木齐 830011; 2.新疆电力建设调试所有限责任公司,新疆 乌鲁木齐 830011; 3.华北电力大学新能源电力系统国家重点实验室,北京 102206)
燃煤锅炉采用选择性催化还原(SCR)脱硝系统会带来厂用电增加及还原剂消耗,增加了运行成本。为使联合运行成本最优,本文在考虑SCR脱硝系统运行成本和锅炉燃煤成本的基础上,结合机组负荷、总给煤量、总风量、一次风压、二次风量、燃尽风量和喷氨量等参数之间的关系,建立了电站锅炉SCR脱硝系统联合运行成本模型,利用粒子群(PSO)算法对一次风压、二次风量、燃尽风量和喷氨量等可调运行参数进行优化,得到不同工况下各参数的最优值。并且采用某1 000 MW发电机组实际运行数据进行模型仿真,结果表明:所建模型具有较好的预测精度和较强的泛化能力,通过优化后机组的联合运行成本可降低3%~5%。
电站锅炉;SCR脱硝;运行成本;运行优化;人工神经网络;PSO算法
燃煤发电过程中排放的NO是雾霾形成的主要原因之一,近年来国家对燃煤电站的NO排放要求日益严格。2015年国家发改委、环保部、国家能源局联合下发《全面实施燃煤电厂超低排放和节能改造工作方案》,规定燃煤电厂NO的排放质量浓度限值为50 mg/m3[1-3]。
为了降低NO排放,目前国内在役和新建大型燃煤机组大部分已安装尾部烟气脱硝装置。在烟气脱硝技术中,选择性催化还原(SCR)脱硝技术因其脱硝效率高、技术成熟,成为燃煤电站的主要脱硝方式[4]。SCR脱硝系统通常采用氨(NH3)做还原剂,稀释空气与NH3混合后经喷氨阀门喷出,并与烟气在催化剂的作用下发生还原反应,生成无害的氮气和水,从而达到烟气脱硝的目的。SCR脱硝系统运行时需不断消耗还原剂NH3,同时稀释风机和制氨设备的运转会带来额外的厂用电损耗,从而给机组的运行成本带来一定的影响[5-6]。
一些学者提出利用燃烧优化技术来降低NO排放量。电站锅炉的NO排放受一次风、二次风和燃尽风等运行参数影响,因此,可以通过人工智能方法建立NO排放与锅炉运行参数之间的关系模型,并通过对可调参数寻优来实现烟气中NO的减排。该方法不需要对锅炉设备进行硬件改造,因此得到了广泛的应用。如有学者提出基于机组历史运行数据,利用人工神经网络(ANN)和支持向量机(SVM)等智能方法建立锅炉NO排放模型[7-9],并基于预测模型,利用遗传算法和粒子群优化(PSO)算法等智能算法优化配风方式等实现锅炉NO的减排[10-12]。但是,若只考虑降低锅炉燃烧时产生的NO,可能会使运行工况偏离设计值,使锅炉效率降低以及煤耗增加。鉴于此,顾燕萍等[13]建立烟气NO排放和锅炉效率的模型,并分别对NO排放和锅炉效率进行优化,但由于 2个目标参数具有不同的量纲,因此并没有讨论整体的最优值;Yang等人[14]考虑锅炉效率以及SCR脱硝系统的喷氨成本、排污费等因素,建立了脱硝系统经济运行模型,但在实际发电过程中,脱硝运行成本不能简单采用排污费来衡量,若烟气NO的含量超过国家排放标准,机组将不允许继续运行。本文在上述研究的基础上,同时考虑烟气NO的脱硝运行成本与锅炉的燃煤成本,基于ANN技术建立锅炉和SCR脱硝联合运行成本模型,并利用PSO算法对参数寻优,实现机组运行成本的最小化。
1 电站锅炉SCR脱硝系统联合运行成本模型
1.1 基本结构
电站锅炉SCR脱硝联合运行成本模型结构如图1所示。整个模型由锅炉燃烧模型、SCR脱硝系统模型和运行成本模型3个子模型组成。
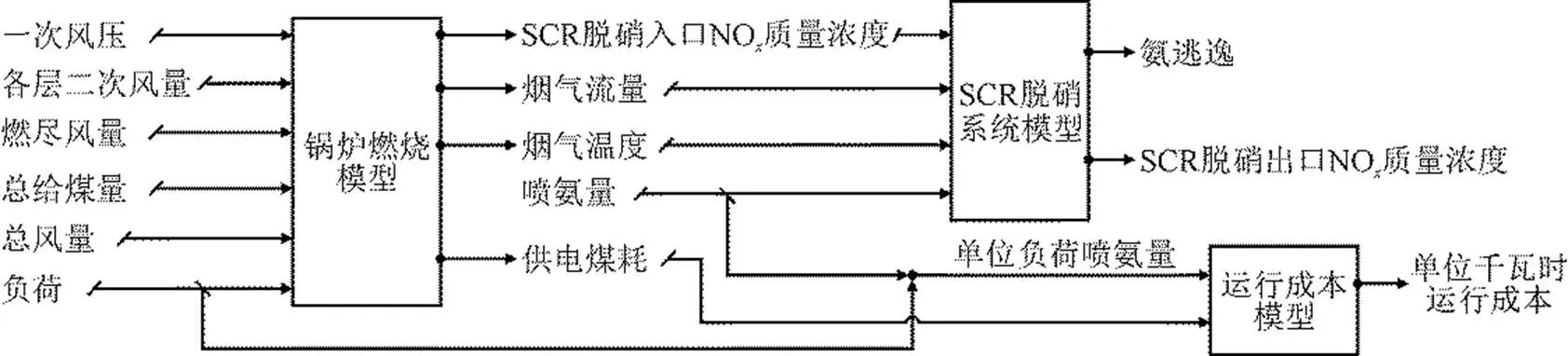
图1 电站锅炉SCR脱硝系统联合运行成本模型结构
为了进行模型训练,从电站厂级监控信息系统(SIS)数据库中,采集机组负荷、总给煤量、总风量、一次风压、各层二次风量、燃尽风量、SCR脱硝入口NO质量浓度、烟气流量、烟气温度、供电煤耗、喷氨量、氨逃逸和SCR脱硝出口NO质量浓度等参数数据作为训练样本,其中供电煤耗数据从SIS性能计算模块中采集。选择影响锅炉燃烧特性的变量作为锅炉燃烧模型的输入,其中包括机组负荷、总给煤量、总风量、一次风压、二次风量、燃尽风量。选择SCR脱硝入口烟气流量、烟气温度、烟气NO质量浓度和供电煤耗作为模型输出。从电站历史运行数据库中采集数据样本,利用BP神经网络进行训练,建立锅炉燃烧模型。
选择影响SCR脱硝反应特性的变量作为SCR脱硝系统模型的输入,包括SCR脱硝入口烟气NO质量浓度、烟气流量、烟气温度和喷氨量,选择氨逃逸、出口NO质量浓度作为模型输出。基于电站运行数据,利用BP神经网络建立SCR脱硝系统模型。在建立以上2个模型后,将与运行经济性相关的供电煤耗(SCR脱硝系统耗电量也体现在供电煤耗中)和单位负荷下喷氨量乘以对应价格,得到单位发电量的运行成本,建立联合运行成本模型。
由图1可见,整个模型同时考虑了锅炉燃烧的经济性和SCR脱硝系统运行的经济性。将模型输入变量中的一次风压、二次风量、燃尽风量以及喷氨量作为可调运行参数,利用PSO算法对其寻优,可实现联合运行成本的最小化。
1.2 BP神经网络建模理论
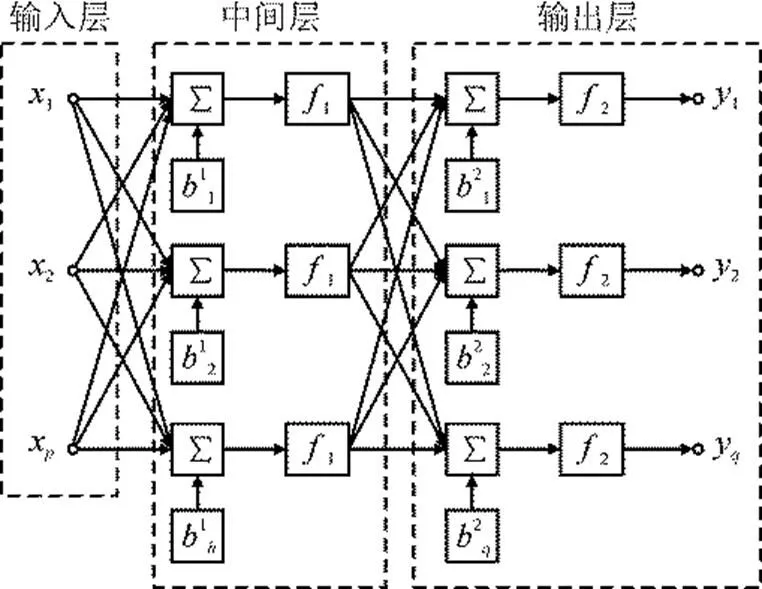
图2 3层神经网络模型结构
根据神经网络理论,每层输入经过加权累加,与一个偏移量相加后,经过激励函数得到输出,即


式(1)—式(2)写成矩阵形式,可得到
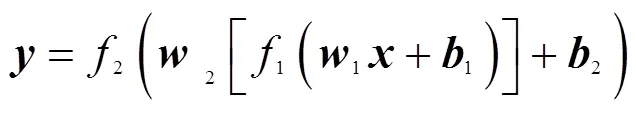
BP神经网络通过反向传播算法实现权值1和2的确定。样本输入值从输入层经过权值和阈值的运算到达隐含层,隐含层经过权值和阈值的运算到达输出层,若输出值与实际值存在偏差,则利用梯度下降法将误差从输出层传递给隐含层再由隐含层到达输入层,逐一对每层的连接权值进行修改,通过不断迭代此过程,将误差降低到允许范围内[15]。在实际计算中,可以利用现有的工具箱,如MATLAB中的ANN工具箱等。
1.3 联合运行成本模型的构建
1.3.1 锅炉燃烧模型
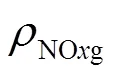

式中,1(·)为8输入4输出的3层BP神经网络函数,用来拟合锅炉燃烧模型的非线性特性。
1.3.2 SCR脱硝系统模型


式中,2(·)为4输入2输出的3层BP神经网络函数,用来拟合SCR脱硝系统模型的非线性特性。
1.3.3 联合运行成本模型




式(6)—式(8)表征所建立的联合运行成本模型包含了锅炉供电煤耗成本和SCR脱硝系统还原剂NH3的成本,即同时考虑了锅炉燃烧的经济性和SCR脱硝运行的经济性。
2 基于PSO算法的联合运行成本模型优化
锅炉SCR脱硝联合运行是为了使联合运行成本最小,因此该问题可以看作以成本模型函数最小为目标的优化问题。PSO算法是一种基于种群的智能优化算法,同其他的进化算法相比,该算法易于实施,全局优化能力更强[16-18]。因此,采用PSO算法对可调运行参数进行优化,使锅炉SCR脱硝系统具有最低的运行成本。
PSO算法中群体的每个粒子代表一个可行解。待优化运行参数为维,群体中第𝑖个粒子的位置记为=[u1,u2, …,u],粒子速度记作=[v1,v2, …,v],所经历的最佳位置为=[p1,p2, …,p],整个群体所经历的最佳位置为g=[g1,g2, …,gd]。粒子在更新过程中,通过动态跟踪个体最优值和群体最优值g来不断调整其位置和速度,具体表示为:
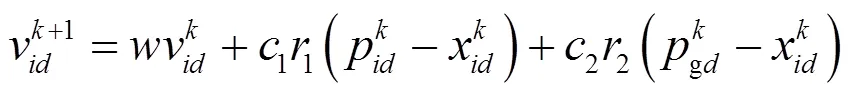


粒子在解空间内不断跟踪个体最优值和全局最优值,直到满足误差标准或达到最大迭代次数为止。粒子在搜索过程中位置限定在[min,max]之内,速度限定在[min,max]之内,以保证群体的全局搜索能力。
为使运行成本最小化,基于PSO算法,优化问题可以表示为:
由此可见,在国家相关政策的支持下,武术国际推广已经成为实现中华民族文化自信的重要内容,与此同时,武术“走出去”的战略实施也为武术对外教材“走出去”创造了空前的机遇。

3 实验结果及分析
3.1 实验设备及数据采集
以某燃煤电站机组直流超超临界1 000 MW锅炉及SCR脱硝系统为研究对象,该锅炉为一次再热、平衡通风、露天布置锅炉,采用四角切圆燃烧系统,共3层二次风门和1层燃尽风门,每层风门开度可实现联调,其中每层二次风门和燃尽风门都有风量测点。同时,为满足环保要求,采用低氮燃烧技术并配备2台SCR脱硝装置(A侧和B侧),布置在锅炉两侧的空气预热器支架上方,在反应器前设置灰斗,不设脱硝旁路烟道,催化剂层数采用2+1布置方式。2台机组共用1套贮氨及输送系统,还原剂采用液氨。为了简化计算,建立A侧SCR系统模型,并认为B侧和A侧SCR系统具有相同特性。
从电站SIS运行数据库采集与上述模型有关参数的数据样本,包括机组负荷、总给煤量、总风量、一次风压、AB、CD、EF 3层二次风量、燃尽风量、喷氨量、SCR脱硝入口烟气流量、烟气温度、烟气NO质量浓度、供电煤耗、氨逃逸、SCR脱硝出口NO质量浓度。采集时间为2014年5月1日到2014年5月14日,采样频率为5 min,共得到约4 000个数据样本。对这些数据进行预处理,包括删除离群点样本和筛选稳态工况,并使得到的样本覆盖较大的负荷范围。稳态工况可以利用滑动窗口法并基于式(12)进行判定[19],

经数据处理后,得到1 420组样本,覆盖工况范围为490~760 MW,其他参数的变化范围见表1。
表1 电站锅炉各参数运行范围

Tab.1 The operating range of parameters of the utility boielr
将所选取的数据分为2组:1 220组样本为训练样本,用来构建锅炉燃烧和SCR脱硝系统的神经网络模型,并得到联合运行成本模型;选择另外200组样本作为测试样本,用来测试模型的预测精度。
3.2 模型预测结果分析


图3 烟气流量预测结果

图4 烟气温度预测结果

图5 SCR脱硝入口NOx质量浓度预测结果
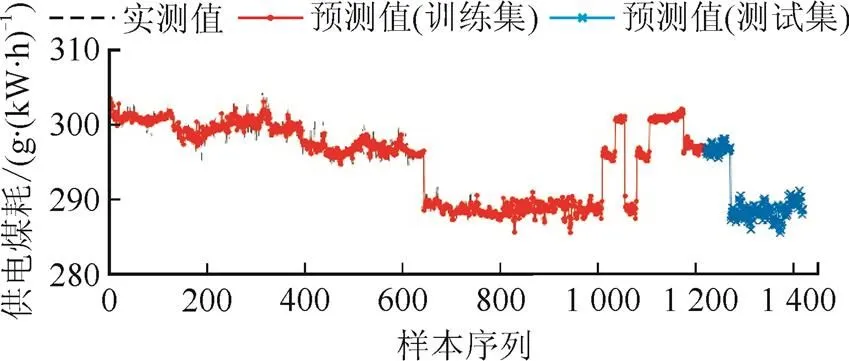
图6 机组供电煤耗预测结果
由图3—图6可以看出:锅炉燃烧模型对训练样本的预测误差非常小,烟气流量、烟气温度、SCR脱硝入口NO质量浓度以及供电煤耗的预测值几乎与实际值重合,表明模型具有较好的逼近能力;同时,锅炉燃烧模型对测试样本的误差也较小,对烟气温度预测时,95.5%的测试样本的预测误差在2 ℃以内;对SCR脱硝入口NO质量浓度预测时,90.5%的测试样本的预测误差低于10 mg/m3。由此可见,建立的模型对新工况也具有较好的预测精度,表明锅炉燃烧模型具有较好的泛化能力。

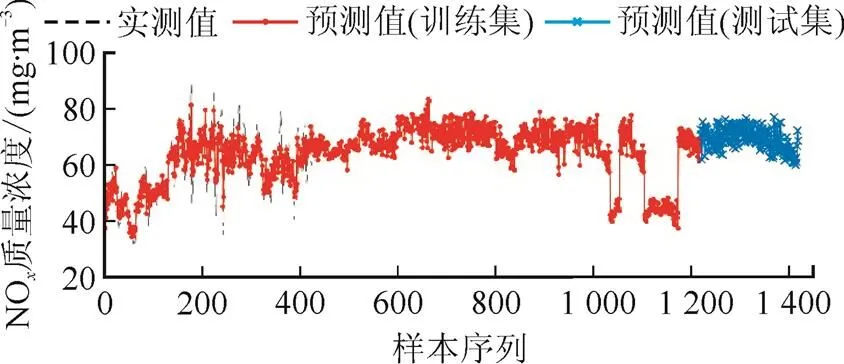
图7 SCR脱硝出口NOx质量浓度预测结果
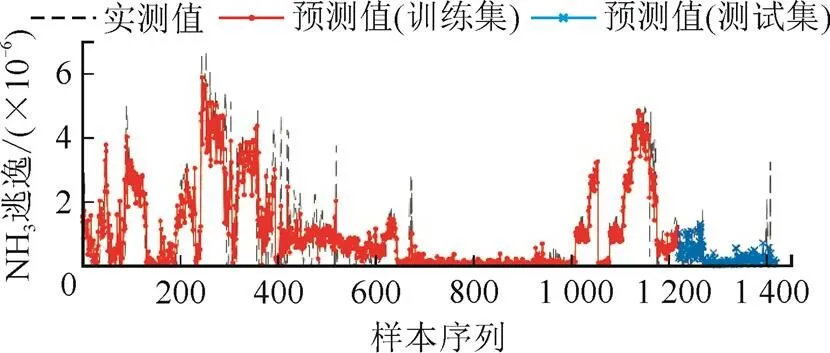
图8 SCR脱硝出口NH3逃逸量预测结果
由图7和图8可以看出,SCR脱硝系统模型对训练样本和测试样本的NO质量浓度和NH3逃逸量的预测值与实际测量值的偏差很小,模型表现出较好的逼近能力和泛化能力。因此,所建立的SCR脱硝系统模型能够实现对NO质量浓度以及NH3逃逸量的精确预测。
为了定量评价建立的锅炉燃烧模型和SCR脱硝系统模型的预测效果,采用平均相对误差ARE和标准化均方根误差NRMSE来衡量模型的预测精度,定义如下:

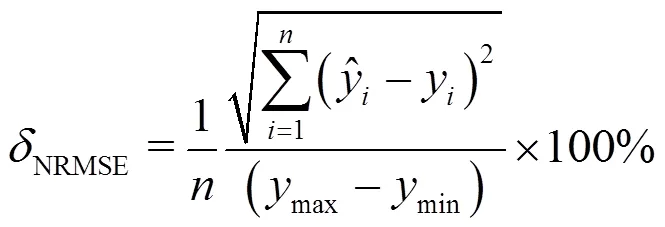
模型中各参数预测误差见表2。表2中锅炉燃烧模型和SCR脱硝系统模型的预测结果与图3—图8一致,所构建模型的预测误差均较低。
表2 模型中各参数预测误差
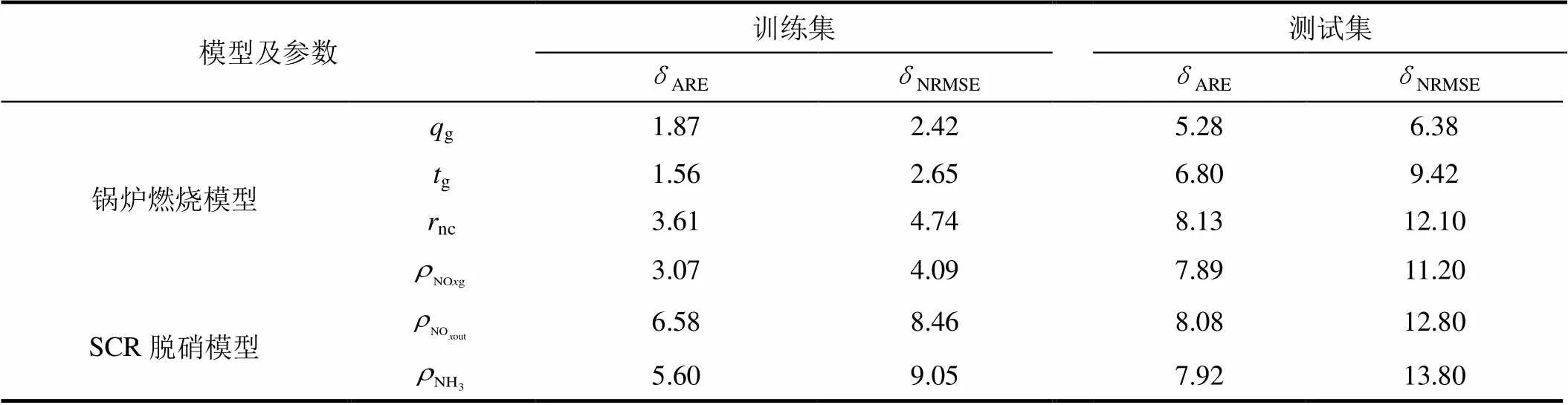
Tab.2 Prediction errors of the parameters %
3.3 模型优化分析


图9 PSO算法迭代过程
对训练样本和测试样本中所有样本工况进行优化,优化结果如图10和图11所示。图10是优化后联合运行成本与未优化的运行成本对比,图11是运行成本降低的比例。由图10和图11可以看出,对于大部分工况样本,经过PSO算法优化后,联合运行成本可以降低3%~5%。
表3 优化前后运行参数变化
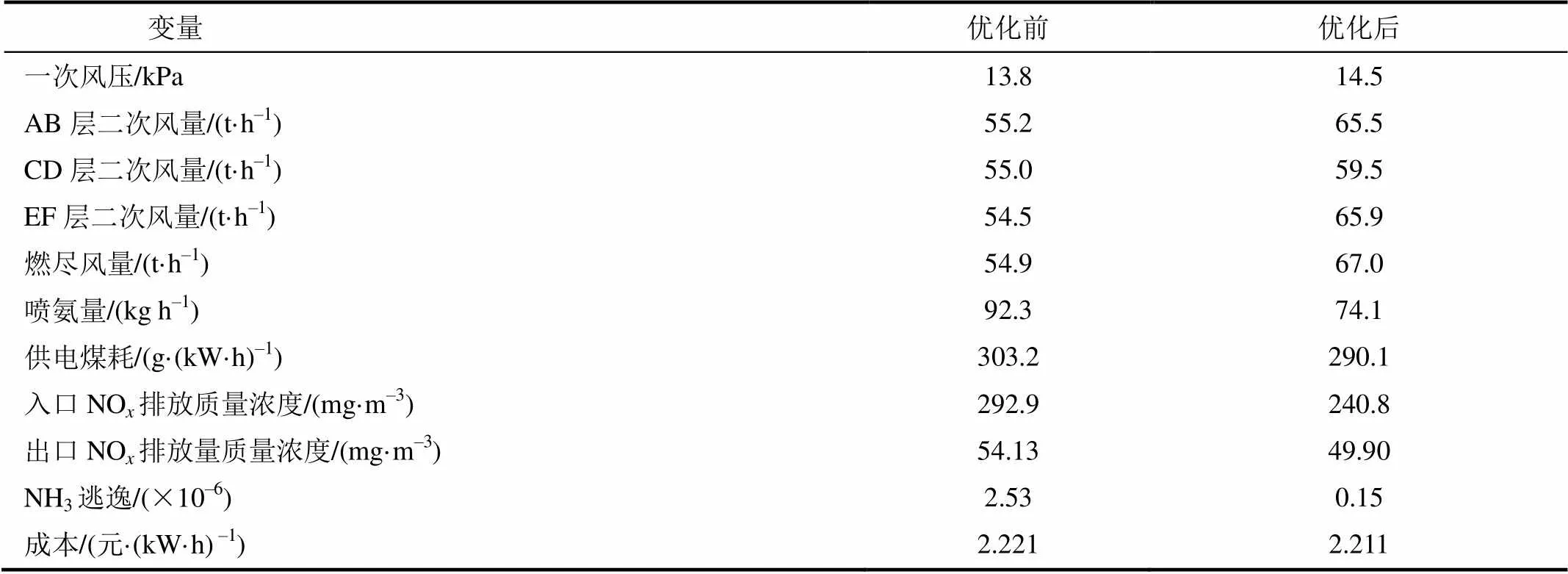
Tab.3 Changes of the operation parameters before and after the optimization
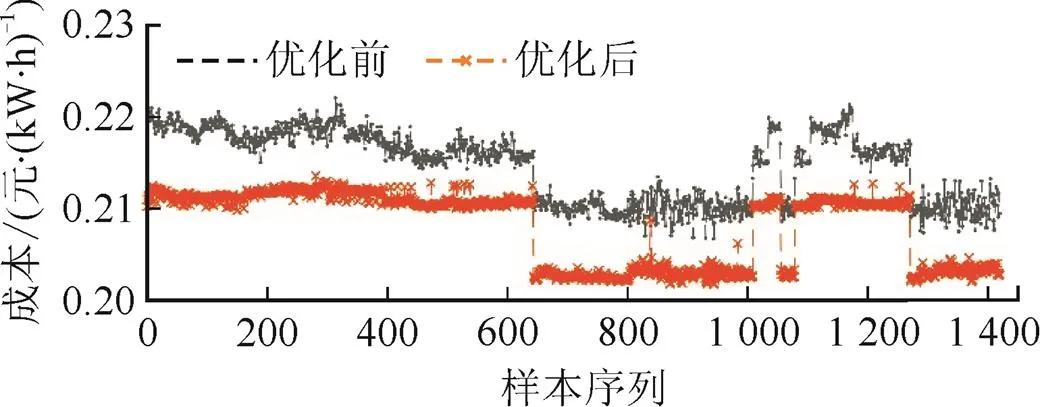
图10 PSO优化前后成本对比
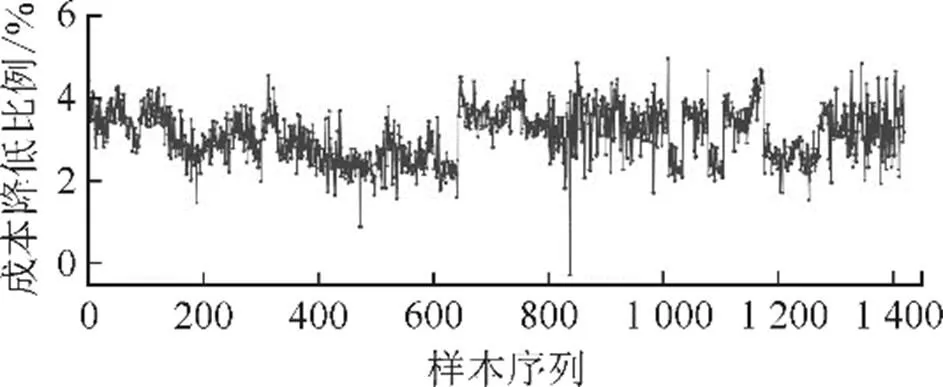
图11 优化后成本降低比例
4 结 语
考虑电站SCR脱硝系统的脱硝成本和锅炉的燃煤成本,将机组负荷、总给煤量、总风量、一次风压、二次风量、燃尽风量和喷氨量等参数作为输入,基于BP神经网络和实际运行数据,建立了锅炉和SCR脱硝系统联合运行成本模型,并利用PSO算法对可调运行参数进行优化,包括一次风压、各层二次风量、燃尽风量和喷氨量,得到不同工况下的最优操作参数。基于某1 000 MW火电机组实际运行数据进行仿真,结果表明通过优化后机组的联合运行成本可降低3%~5%,同时能满足NO和NH3的排放要求。
[1] 姚明宇, 聂建平, 张立欣, 等. 燃煤电站锅炉烟气污染物一体化协同治理技术[J]. 热力发电, 2016, 45(3): 8-12. YAO Mingyu, NIE Jianping, ZHANG Lixin, et al. Integrative flue-gas pollutants removal technology for coal-fired utility boilers[J]. Thermal Power Generation, 2016, 45(3): 8-12.
[2] 姚楚, 龙东腾, 吕游, 等. 火电厂SCR脱硝系统机理建模与控制研究[J]. 热能动力工程, 2018, 33(5): 78-84. YAO Chu, LONG Dongteng, LV You, et al. Study on mechanism modelling and control of SCR denitration system in thermal power plant[J]. Journal of Engineering for Thermal Energy and Power, 2018, 33(5): 78-84.
[3] 武宝会, 李帅英, 牛国平, 等. 燃煤机组烟气污染物协同脱除技术及应用[J]. 热力发电, 2017, 46(11): 103-107. WU Baohui, LI Shuaiying, NIU Guoping, et al. Synergistic removal technologies for flue gas pollutants and their engineering applications in coal-fired units[J]. Thermal Power Generation, 2017, 46(11): 103-107.
[4] 梁俊杰, 张战锋, 周健, 等. SCR烟气脱硝系统运行全过程数据分析[J]. 热力发电, 2018, 47(12): 93-99. LIANG Junjie, ZHANG Zhanfeng, ZHOU Jian, et al. Analysis on whole process operation data of SCR flue gas denitration system[J]. Thermal Power Generation, 2018, 47(12): 93-99.
[5] 卞韶帅, 余海燕, 杨士华, 等. 锅炉低氮燃烧与SCR脱硝联合运行优化系统[J]. 热力发电, 2016, 45(8): 81-86. BIAN Shaoshuai, YU Haiyan, YANG Shihua, et al. Optimization on combined operation of low-NOcombustion and SCR denitration system in utility boilers[J]. Thermal Power Generation, 2016, 45(8): 81-86.
[6] 成新兴, 武宝会, 周彦军, 等. 燃煤电厂超低排放改造方案及其经济性分析[J]. 热力发电, 2017, 46(11): 97-102. CHENG Xinxing, WU Baohui, ZHOU Yanjun, et al. Ultra-low emission reform scheme for coal-fired power plants and its economic analysis[J]. Thermal Power Generation, 2017, 46(11): 97-102.
[7] 赵文杰, 张楷. 基于互信息变量选择的SCR烟气脱硝系统非线性自回归神经网络建模[J]. 热力发电, 2018, 47(9): 22-26. ZHAO Wenjie, ZHANG Kai. NARX neural network modeling of SCR denitration system based on mutual information variables selection[J]. Thermal Power Generation, 2018, 47(9): 22-26.
[8] 钟用禄, 李海山, 刘发圣, 等. 基于PCA-SVR的燃煤锅炉NO排放预测[J]. 热力发电, 2015, 44(1): 87-90. ZHONG Yonglu, LI Haishan, LIU Fasheng, et al. PCA-SVR model based NOemissions prediction for coal-fired boilers[J]. Thermal Power Generation, 2015, 44(1): 87-90.
[9] 陆军, 张广才, 徐党旗, 等. 改进BP神经网络在低氮燃烧优化中的应用[J]. 热力发电, 2015, 44(4): 106-111.LU Jun, ZHANG Guangcai, XU Dangqi, et al. Application of modified BP neural network in optimization of low NOcombustion for a pulverized coal boiler[J]. Thermal Power Generation, 2015, 44(4): 106-111.
[10] 凡荣荣, 姚翠兰, 杨巨生, 等. 基于PSO优化锅炉氮氧化物的排放[J]. 热力发电, 2012, 41(8): 28-31. FAN Rongrong, YAO Cuilan, YANG Jusheng, et al. Application of PSO in NOemission from boiler[J]. Thermal Power Generation, 2012, 41(8): 28-31.
[11] 董建勋, 张海福, 马志杰, 等. 燃烧优化系统在 600 MW机组锅炉控制中的应用[J]. 热力发电, 2012, 41(4): 81-82. DONG Jianxun, ZHANG Haifu, MA Zhijie, et al. Loop combustion optimizing control technology on 600 MW thermal power unit[J]. Thermal Power Generation, 2012, 41(4): 81-82.
[12] 刘吉臻, 吕游, 杨婷婷. 基于变量选择的锅炉NO排放的最小二乘支持向量机建模[J]. 中国电机工程学报, 2012, 32(20): 102-107. LIU Jizhen, LV You, YANG Tingting. Least squares support vector machine modeling on NOemission of boiler based on variable selection[J]. Proceedings of the CSEE, 2012, 32(20): 102-107.
[13] 顾燕萍, 赵文杰, 吴占松. 基于最小二乘支持向量机的电站锅炉燃烧优化[J]. 中国电机工程学报, 2010, 30(17): 91-97. GU Yanping, ZHAO Wenjie, WU Zhansong. Combustion optimization for utility boiler based on least square-support vector machine[J]. Proceedings of the CSEE, 2010, 30(17): 91-97.
[14] YANG T, CUI C, SHEN Y, et al. A novel denitration cost optimization system for power unit boilers[J]. Applied Thermal Engineering, 2016, 96: 400-410.
[15] 陈鸿伟, 吴晶, 何骏鹏, 等. 基于GA-BP对锥形布风板双流化床颗粒循环流率的预测研究[J]. 热力发电, 2015, 44(2): 90-92. CHEN Hongwei, WU Jing, HE Junpeng, et al. GA-BP algorithm based prediction of solids circulation rate in a dual fluidized bed with conical gas distributor[J]. Thermal Power Generation, 2015, 44(2): 90-92.
[16] KENNEDY J, EBERHART R. Particle swarm optimiza- tion[C]//Proceedings of IEEE International Conference on Neural Networks. Perth: IEEE Press, 1995: 1942- 1948.
[17] 方贤, 铁治欣, 崔仕文, 等. 基于粒子群优化双支持向量机的SCR烟气脱硝效率预测模型[J]. 热力发电, 2018, 47(1): 53-58. FANG Xian, TIE Zhixin, CUI Shiwen, et al. Model for predicting SCR flue gas denitration efficiency based on particle swarm optimization and twin support vector machine[J]. Thermal Power Generation, 2018, 47(1): 53-58.
[18] 赵越, 蒙毅, 李仁义. 基于粒子群优化算法分析约束条件对配煤最优价格的影响[J]. 热力发电, 2017, 46(12): 99-104.ZHAO Yue, MENG Yi, LI Renyi. Influence of constraints on optimal price of blending coal: by particle swarm optimization algorithm[J]. Thermal Power Generation, 2017, 46(12): 99-104.
[19] LV Y, LIU J, YANG T, et al. A novel least squares support vector machine ensemble model for NOemission prediction of a coal-fired boiler[J]. Energy, 2013, 55: 319-329.
Optimization model for combined operation of SCR denitration system in utility boiler
LI Wei1, XU Qiang1, KONG Dean1, ZHAO Xiang1, GAO Ning2, LYU You3
(1. State Grid Xinjiang Electric Power Research Institute, Urumqi 830011, China; 2. Xinjiang Electric Power Construction Debugging Institute Limited Liability Company, Urumqi 830011, China; 3. State Key Laboratory of Alternate Electric Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China)
Applying selective catalytic reduction (SCR) flue gas denitration system in coal-fired boiler will increase the auxiliary power and reducing agent consumption, and increase the operation cost. To reduce the operation cost, this paper establishes an operation cost model for the boiler and SCR denitration system by using the parameters including the unit load, total coal feed rate, total air volume, primary air pressure, secondary air rate, over fire air rate and ammonia injection rate, on the basis of considering the operation cost of the SCR denitration system and fuel cost of the boiler. The particle swam optimization (PSO) algorithm is proposed to optimize the adjustable parameters such as the primary air pressure, secondary air rate, over fire air rate and the ammonia injection rate, thus the optimal values of each parameter under different conditions are obtained. Moreover, simulation experiments were carried out by using the operation data of a 1 000 MW thermal power plant, and the results show that, the established model has good prediction precision and strong generalization ability, the combined operation cost of the unit after optimization can be reduced by 3%~5%.
utility boiler, SCR denitration, operation cost, operation optimization, artificial neural network, particle swam optimization algorithm
National Natural Science Foundation of China (51606063)
李伟(1972—),男,高级工程师,主要研究方向为热工自动化及供热技术,liwei7117@126.com。
TK223
A
10.19666/j.rlfd.201812221
李伟, 徐强, 孔德安, 等. 电站锅炉SCR脱硝系统联合运行优化模型[J]. 热力发电, 2019, 48(6): 46-52. LI Wei, XU Qiang, KONG Dean, et al. Optimization model for combined operation of SCR denitration system in utility boiler[J]. Thermal Power Generation, 2019, 48(6): 46-52.
2018-12-27
国家自然科学基金青年项目(51606063)
吕游(1987—),男,博士,讲师,主要研究方向为电站数据分析、建模及优化,you.lv@hotmail.com。
(责任编辑 杜亚勤)

