膜盘联轴器燃气轮机发电机组转子系统动力学分析
甄 满,孙 涛,田拥胜,张华良,谭春青
(1. 中国科学院工程热物理研究所,北京 100191;2. 中国科学院大学,北京 100191)
传统的燃气轮机发电机组多采用燃气轮机转子-减速齿轮箱-低速发电机转子的轴系结构,而新一代发电机组则采用共轴直驱式的耦联转子结构,通过弹性联轴器将高速电机和燃气轮机转子直接联接,使系统的体积减小、重量大大减轻,机械损耗也随之减少,成为燃气轮机发电机组提高功率密度、机组效率和改善机组性能的有效途径。对于弹性联轴器联接的直驱式燃气轮机发电机组耦联转子系统而言,耦联转子系统的动力学特性对转子系统的稳定运行具有重要的影响。因此,深入研究直驱式双跨转子系统的动力学特性具有重要的意义。
目前国内外学者对耦联转子系统开展了大量研究,聂志雄等人[1]分析了不同联轴器联接的转子系统的临界转速,发现柔性联轴器联接的转子系统的临界转速最低。闻雪友[2]研究了带膜盘联轴器转系的临界转速,分析了膜盘弹性曲率、中间轴长和膜盘布置位置对临界转速的影响。李小彭等人[3]分析了膜片联轴器联接的多跨转子系统的临界转速,发现转子系统的临界转速主要由弯扭振动的轴段决定。为减小双跨转子系统的共振振幅,王晨阳等人[5]研究了转子吸振器对多跨转子的影响,发现转子吸振器能够有效地避免多跨转子系统的临界共振。丁千等人[6]研究了双跨转子系统油膜稳定的问题,发现了不同于单跨转子系统的双低频现象。赵明等人[7]采用传递矩阵法研究了扭振、畸形结构、油膜刚度、油膜阻尼等因素对临界转速的影响。高金吉等人[8]采用空心轴段代替联轴器,使用有限元方法分析了多跨转子系统的临界转速,发现转子系统的临界转速有不同程度的提高。师树谦等人[9]分析了圆柱滚子轴承耦联的双轴系转子,结果表明由圆柱滚子轴承耦联的双驱动轴系,其固有频率比单轴系固有频率来说较小并通过锤击实验验证了结果。文献[9-11]针对双转子临界转速和流场进行了分析,为双转子设计和改善提供了依据。
Rigaud和Sabot[12]分析了弹性轴、轴承和联轴器刚度等因素对齿轮传动系统临界转速的影响。Crastiu等人[13]采用理论和实验相结合分析了单转子和三转子轴系的临界转速。Prabhakar等人[14]将联轴器等效为无摩擦的联轴节分析了转子系统跨越临界转速时的振动响应。Luo[15]分析了基础松动对多转子系统的影响,转子响应呈现出周期性和高次谐波分量。以上建模方法,对于联轴器刚度对其临界转速和不平衡响应的影响很少涉及。
本文针对某舰用1+1/2式高速直驱式燃气轮机发电机组,如图1所示,建立了燃气轮机转子-膜盘联轴器-发电机转子系统计算模型,通过有限元方法分析了单跨转子与双跨转子系统间存在的联系和不同膜盘联轴器刚度下动力学特性,分析结果可以对双跨转子系统的设计提供一定的理论参考。

图1 共轴直驱式燃气轮机发电机组
1 双曲线型面膜盘联轴器
1.1 双曲线型面膜盘联轴器结构模型
膜盘联轴器作为带有金属元件的联轴器具有结构简单、重量轻、无需润滑且柔性好的特点。在工业和海洋领域中,常作为燃气轮机、汽轮机和高速的离心压缩机动力传递部件[16],其型面结构形式如图2所示。

图2 双曲线型面膜盘
型面厚度计算公式可表示为:
t=ta/(r/ra)2
(1)
式中:ra为膜盘的外半径,ta为外半径厚度,r为膜盘半径。
以某型舰用燃气轮机发电机组采用的双曲线型面膜盘联轴器为研究对象,根据膜盘联轴器的基本结构参数,对膜盘联轴器进行建模。结构参数如表1所示,三维模型如图3所示,该联轴器由2个直径比为0.4和2个直径比为0.5的膜盘串联组成。
1.2 联轴器刚度计算
由于膜盘为厚度变化的薄圆盘,变形较大,所以计算时需考虑大变形导致膜盘刚度变化的非线性。

表1 膜盘联轴器结构参数

图3 双曲线型面膜盘联轴器3D模型
为测量联轴器的刚度,通过建立联轴器的三维模型,根据膜盘联轴器在工况下的受力状态,左端施加固定约束,如图4所示。计算得到联轴器的变形量,根据载荷与变形量的关系求解联轴器的轴向刚度、径向刚度和角向刚度,位移云图如图5和图6所示。
假设该型燃气轮机在额定工况工作时,其轴向力约为1.1 kN,径向力约为0.6 kN,弯矩为10 N·m,扭矩为350 N·m。以轴向刚度有限元的分析结果为例,画出整体联轴器轴向位移和轴向反力关系图,如图7所示。然后采用多项式方程拟合数据曲线,发现二次多项式具有较好拟合效果,得到数据线的拟合方程f(x)=2×107x2+1.68×105x+46,则得到联轴器轴向刚度表达式(2),由表达式可知,刚度值随轴向偏移的增大而增大,通过计算,在工况下联轴器的轴向刚度值为3.28×105N/m。如果采用线性刚度模型描述膜盘联轴器轴向刚度为2.73×105N/m,误差为16.77%,因此采用非线性描述联轴器刚度是必要的。

图4 载荷和边界约束

图5 膜盘受轴向力位移云图

图6 膜盘受弯矩位移云图
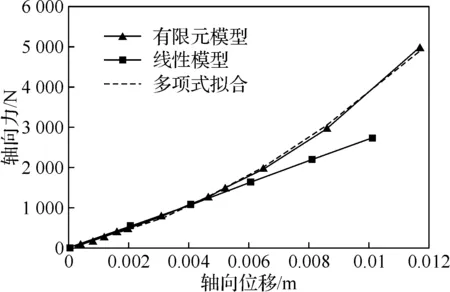
图7 联轴器有限元和多项式拟合结果对比
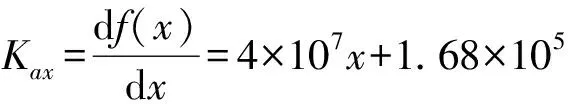
(2)
通过对轴向非线性刚度的分析,采用同样的方法可以得出工况下的径向和扭转刚度。求得膜盘联轴器径向刚度Kri=6.02×104N/m,轴向刚度Kax=3.28×105N/m,角向刚度为Kan=1.17×103N·m/rad,扭转刚度为Kto=5.7×105N·m/rad。本文后续的分析结果均以工况为基准,给出刚度变化的百分比。本文选择了T/OD、ID/OD和L/OD作为三种变化参量,研究外径厚度、内外径比和中间轴长对刚度的影响,其中T/OD表示外径厚度和外径的比,ID/OD表示内径和外径的比,L/OD表示中间轴长和外径的比。无量纲刚度变化定义式为:(某工况刚度值-额定工况刚度值)/额定工况刚度值。
外径厚度对膜盘联轴器来说是一个重要的结构参数。图8给出了不同膜盘的外径厚度下,该联轴器轴向刚度、径向刚度、角向刚度和扭转刚度的变化百分比。

图8 联轴器刚度随外径处厚度变化
结果表明:膜盘联轴器的轴向刚度、径向刚度、角向刚度和扭转刚度随着厚度的增加而增大且变化较为明显。膜盘的外径厚度增大后,膜盘整体厚度增加,承受应力的面积增加,导致膜盘的刚度增加。
图9为轴向刚度、径向刚度、角向刚度和扭转刚度随着内外直径比的变化百分比。轴向刚度、径向刚度和角向刚度随内外直径比的增大而增大,而扭转刚度变化不大。这是由于膜盘内外径比变小,相对变形面积减小,刚度变大,而扭转刚度主要和膜盘最薄厚度处的截面积有关,因此内外径比对扭转刚度影响不明显。

图9 联轴器刚度随内外径变化
图10为膜盘联轴器轴向刚度、径向刚度、角向刚度和扭转刚度随着中间轴长度变化的百分比。膜盘联轴器的径向刚度、角向刚度和扭转刚度随着中间轴长增大而减小,轴向刚度基本不变。其原因在于膜盘联轴器的轴向刚度主要取决于串联的膜盘而与中间轴长度的关系不大。中间轴长度增大,沿轴向的转角、径向位移和弯曲角度增加,导致膜盘联轴器的径向、角向和扭转刚度变小。

图10 膜盘联轴刚度随中间轴长变化
2 耦联转子系统数值计算
2.1 数值计算方法
Newmark-β法是把时间离散化,然后在一系列的时间步长Δt上对方程进行数值积分。假设:
(3)
(4)
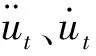
(5)
2.2 数值计算验证
为了验证自编程序的准确性和计算能力,分别采用自编程序和ANSYS软件对电机转子进行临界转速计算,几何模型和有限元模型如图11所示。
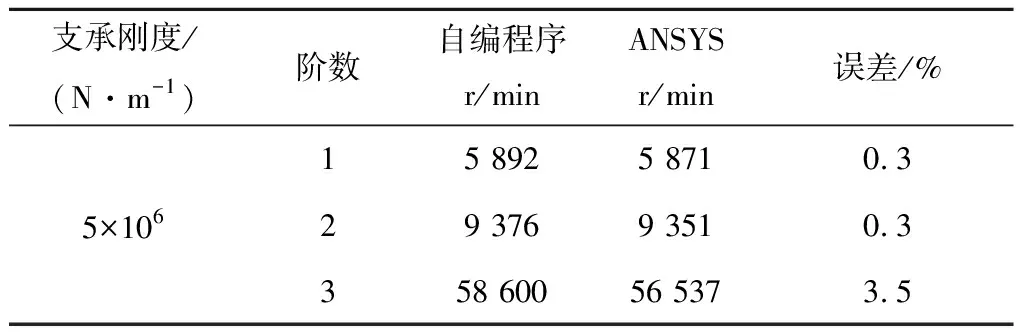
将ANSYS和自编程序的计算结果进行对比,结果对比如表2所示,可以看出,采用MATLAB自编程序和ANSYS计算的临界转速误差在5%范围内,具有较高的可信度,可满足后续分析的要求,误差的来源主要是采用软件计算时,网格的密度远大于自编程采用的单元个数。
采用自编程序得到电机转子模态振型图,如图12所示,从图中可以看出电机转子前四种模态为平动模态、锥动模态、一阶弯曲模态和二阶弯曲模态。

(a) 电机转子3D模型
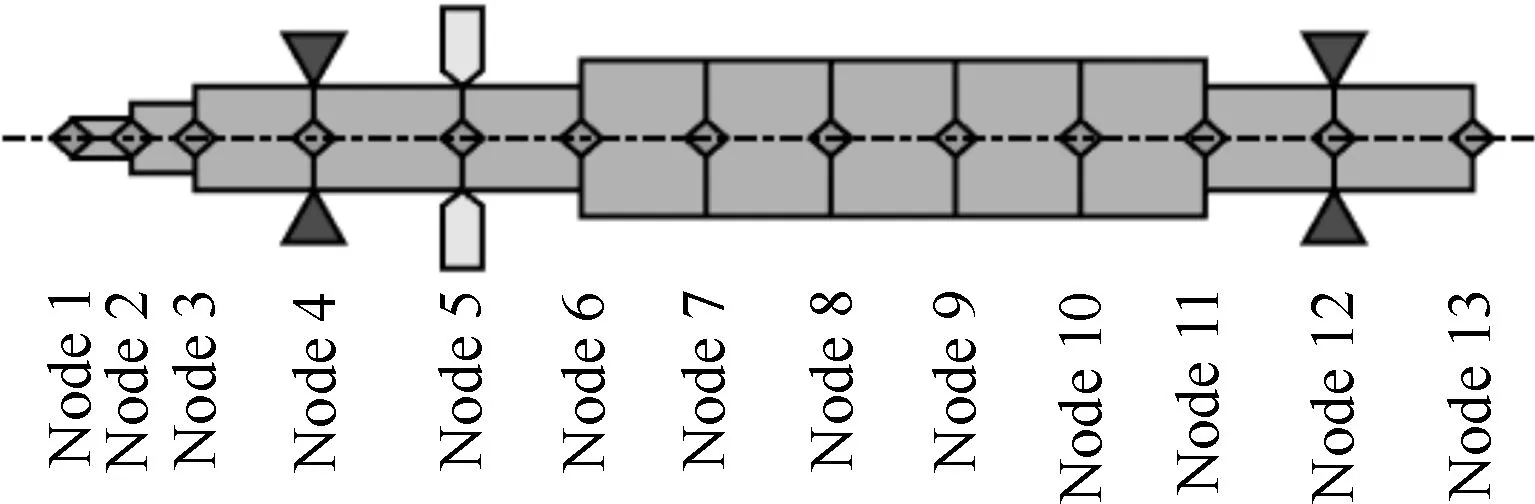
(b) 电机转子有限元模型图11 电机转子模型
支承刚度/(N·m-1)阶数自编程序r/minANSYSr/min误差/%5×10615 8925 8710.329 3769 3510.3358 60056 5373.5

图12 电机转子模态振型
2.3 耦联转子计算模型
耦联转子系统是由电机转子和高压转子通过膜盘联轴器联接,如图13所示,把转子系统划分为23段,24个节点,轴段采用等参梁单元,轮盘采用质点单元,每个节点具有x、y方向平动和转动4个自由度,整个系统共有96个自由度。模型中的柔性膜盘联轴器根据式(6)等效质量的原则简化成一轴段固结在转子上,等效直径为D0。
(6)
式中:m、L和ρ分别为联轴器质量、联轴器的总长和轴段密度。

图13 耦联转子系统有限元模型
通过MATLAB软件自编程建立有限元计算模型,转子动力学方程可表示为:
SMT基本流程是焊膏印刷、贴装、回流焊接、清洗、检测。焊膏印刷作为SMT中的第一道工序,它直接影响着后序工艺,并决定着产品的可靠性。据统计,60%-70%的焊接缺陷都是由不良的焊膏印刷结果造成的[1]。为了解决上述问题,本文设计并实现了对焊膏印刷机关键参数实时分析的软件。

(7)

其中刚度矩阵K为:
联轴器刚度矩阵KC为[17]:

3 耦联转子系统动力学分析
3.1 临界转速和不平衡响应
耦联转子系统的临界转速与单转子系统存在联系和区别。在电机转子系统中,轴承刚度根据经验设为5×106N/m,高压转子系统的轴承刚度设置为6×107N/m。根据2.3节的计算模型,求解运动微分方程的齐次解,得到双跨转子系统的临界转速和模态振型,如表3和图14所示。
以前几阶临界转速为例,计算单转子系统的前临界转速和耦联系统的临界转速,从表中可以看出,耦联系统的临界转速在原有的单转子系统的临界转速上有不同程度的增加。这是因为当单转子系统通过联轴器联接时,联接点的角位移和线位移要连续,这相当于在原有的转子系统上添加额外的约束,导致系统的刚度有所增加,临界转速也会提高。
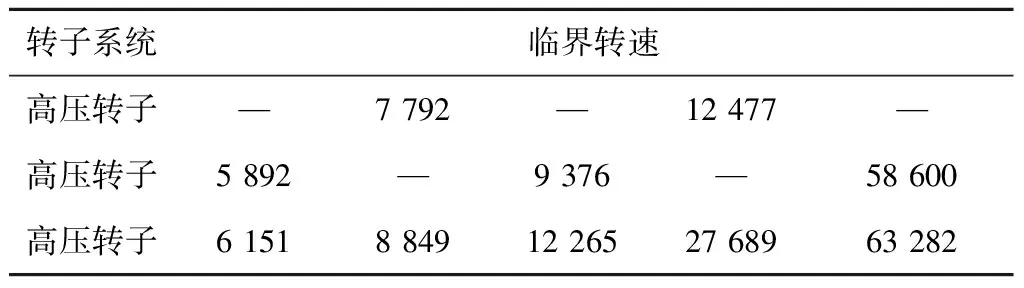
表3 单转子和耦联转子系统临界转速结果对比 r/min
图14是耦联系统的前六阶模态振型,从图中可以看出,耦联系统的模态振型和单转子系统存在联系,耦联系统的第一阶模态振型为电机转子的锥动模态,第二阶模态为高压涡轮转子和电机转子锥动模态的耦合。第三阶模态和第四阶模态是电机转子的锥动、一阶弯曲和高压涡轮转子的一阶、二阶弯曲模态的耦合。第五阶模态是电机转子的二阶弯曲模态,第六阶对应的是高压转子的三阶弯曲模态。
通过对耦联系统的临界转速和模态分析,可以估计单转子系统组合后转子系统的临界转速的分布情况,同时可以估计耦联后的系统在每一阶的主振型中,哪一个单转子系统的振动更加明显。

图14 耦联转子系统的模态振型
为分析耦联转子系统和单转子系统的不平衡响应。假设电机转子圆盘和高压转子圆盘有1 mm的偏心率,用来模拟转子系统的不平衡响应,耦联转子系统联接点处有额外的约束,导致系统的临界转速发生变化。选取节点12和节点17处轴承的振动情况。图15给出了单转子系统和耦联转子系统的不平衡响应的对比。从图中可以看出在低转速时,耦联转子系统不平衡响应在相同不平衡状态下比单转子系统的振幅要小。在高转速时,耦联转子系统不平衡响应在相同不平衡状态下比单转子系统的振幅要大。电机转子系统不平衡引起的同步振动主要反映在平动模态和锥动模态附近。耦联的电机转子系统对耦联系统的第六阶模态反映敏感。高压转子系统对第三阶转子系统模态敏感,耦联的高压转子系统对耦联转子系统的第六阶模态敏感。

(a) 联轴器左端轴承处
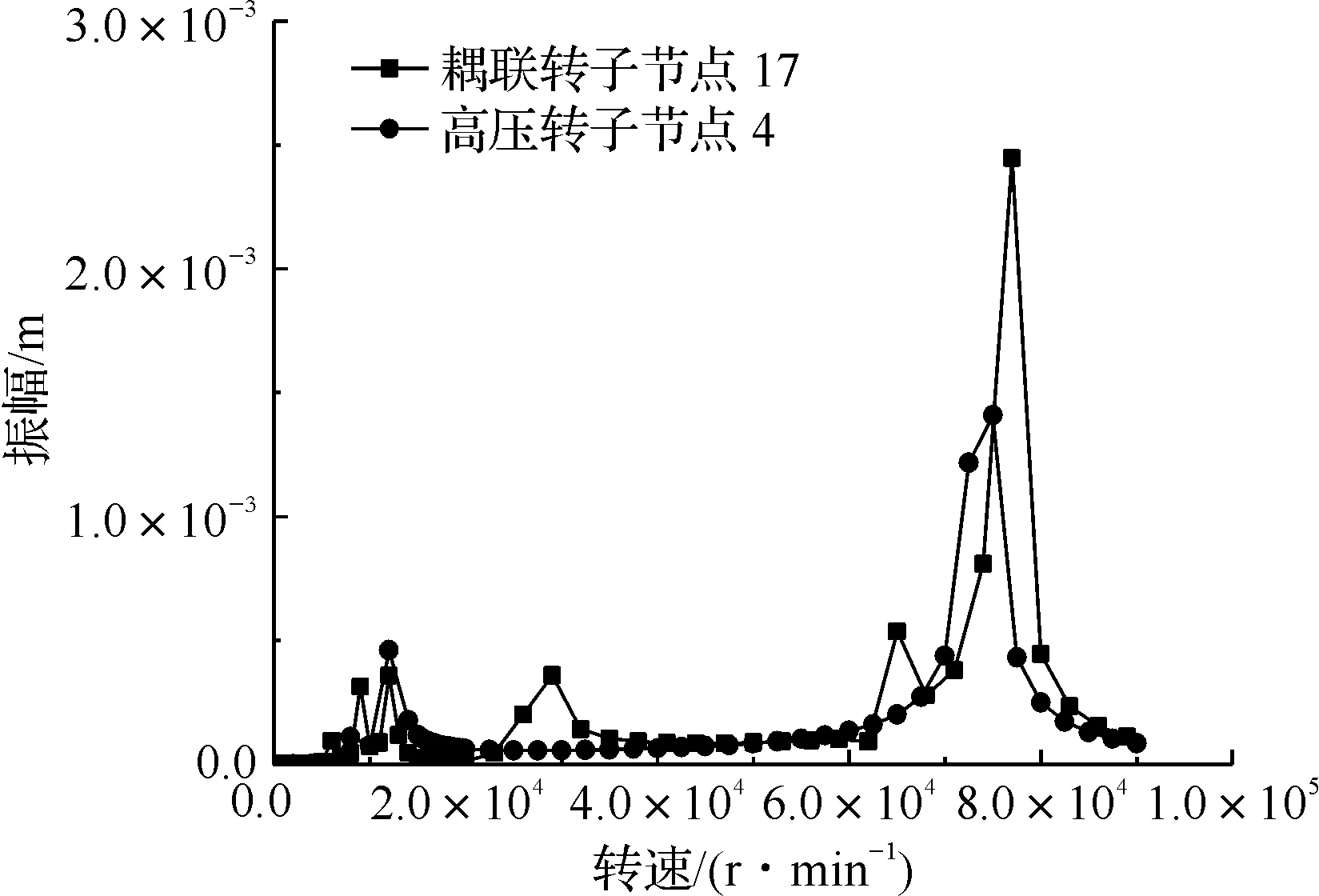
(b) 联轴器右端轴承处图15 单转子系统和耦联转子系统的不平衡响应对比
为了分析不平衡位置和大小对耦联转子系统的影响。通过讨论系统工作在20 000 r/min时,改变耦联转子系统中电机转子上圆盘和高压转子圆盘偏移量,系统振幅随偏移量改变的趋势,如图16所示,联轴器左轴承12节点对盘1的不平衡量较为敏感,而联轴器右轴承17节点对盘2的不平衡量较为敏感。
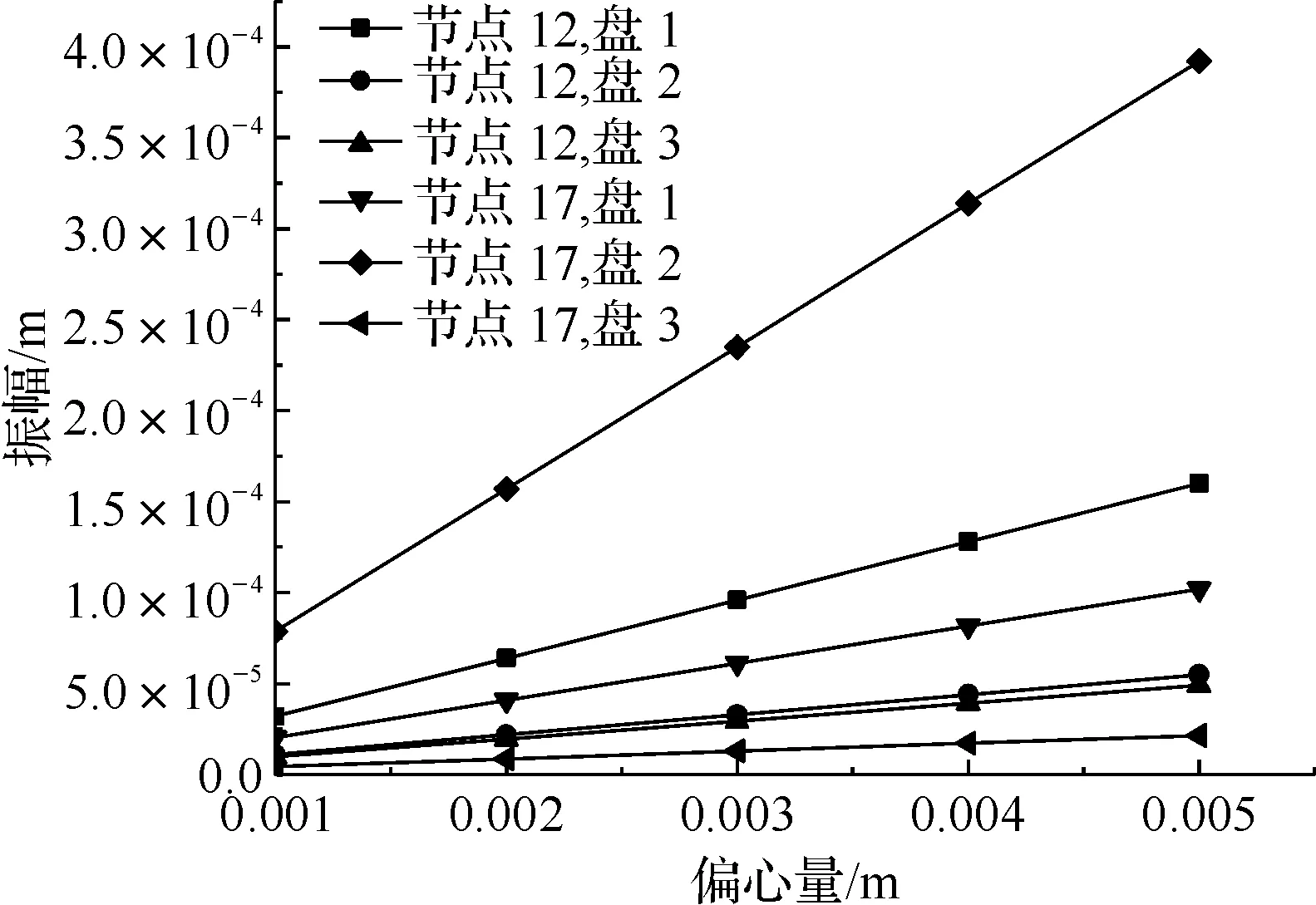
图16 耦联转子系统不平衡位置和大小响应对比
3.2 联轴器刚度对耦联转子系统的影响
由于燃气轮机发电机组会出现变工况的情况,燃气轮机的工作状态和受力情况可能会发生变化,引起联轴器刚度的变化。因此有必要研究刚度变化会对耦联转子系统的动力学特性的影响。为分析联轴器刚度对耦联转子系统的影响,采用不同的刚度组合分析的耦联转子系统的前三阶固有频率。图17为膜盘联轴器刚度对耦联系统前三阶固有频率的影响。从图中我们可以看出,联轴器刚度的增加会提高耦联转子系统的临界转速,第一阶和第三阶临界转速受径向刚度的变化影响明显,径向刚度的增加会提高耦联系统的第一和第三阶临界转速,而角向刚度的增加对其影响较小。径向刚度和角向刚度的变化对耦联转子系统的第二阶临界转速影响都较为明显,刚度的增加会提高耦联转子系统的第二阶临界转速。

(a) 第一阶

(b) 第二阶

(c) 第三阶图17 耦联转子系统的前三阶临界转速随刚度的变化
为了分析联轴器对耦联转子系统的不平衡响应,通过不同组合的联轴器刚度来研究系统的不平衡响应,如表4所示。图18和图19给出了三个不同位置圆盘施加相同不平衡质量后联轴器左端支承处和右端支撑处的振动响应曲线。从图中可以看出,联轴器刚度的增加会提高轴承处的振动响应幅度。径向刚度的增加对耦联转子系统的第四阶和第五阶临界转速的振幅影响较大。角向刚度的增加对耦联转子系统的第二阶和第五阶临界转速的振幅影响较为明显,其中角向刚度的变化对耦联转子系统的第五阶临界转速的振幅影响最为明显。

表4 不同联轴器刚度的组合
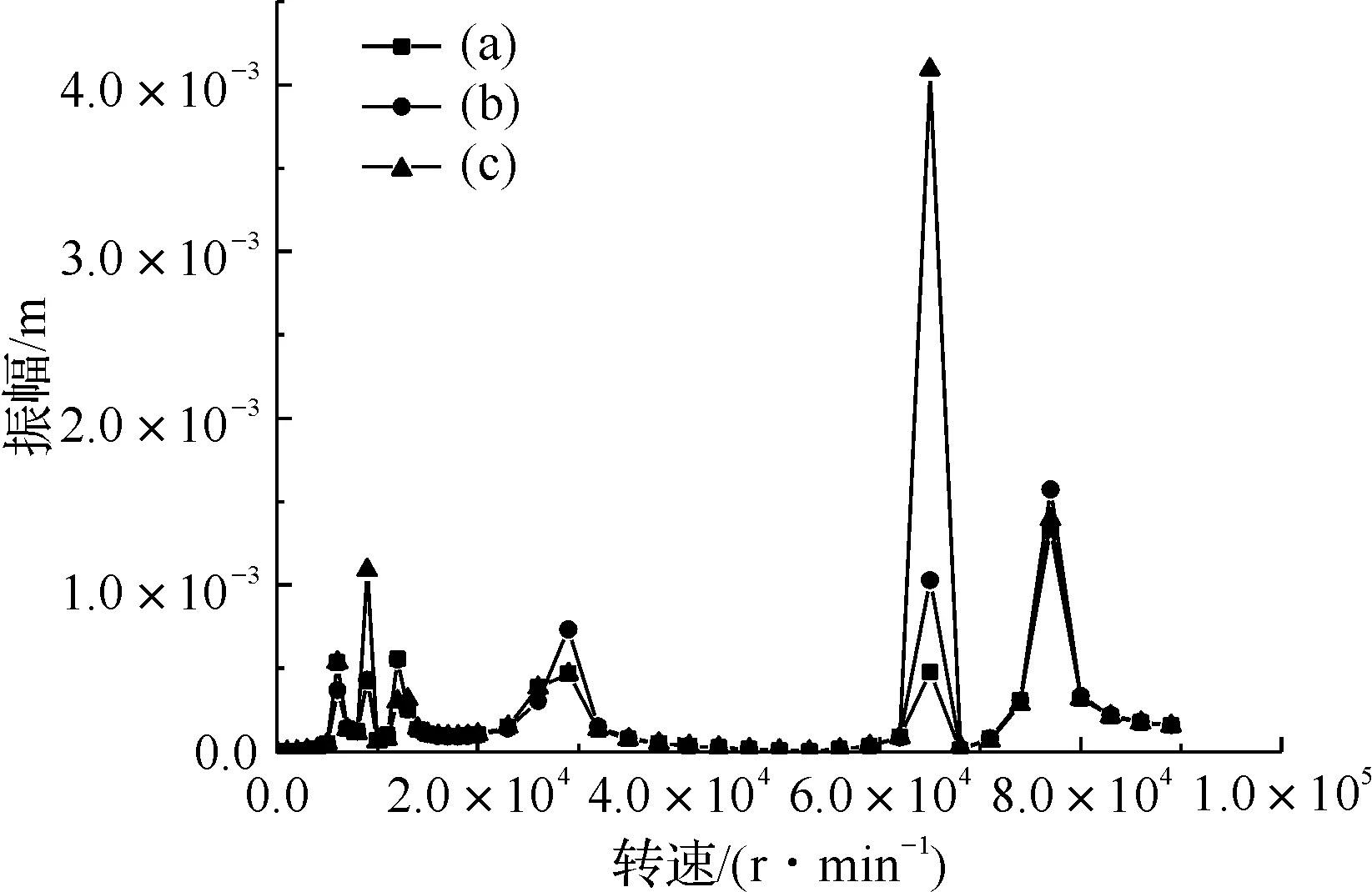
图18 不同组合刚度下节点12的振动响应

图19 不同组合刚度下节点17的振动响应
4 结论
本文构建了电机转子和高压涡轮转子采用膜盘联轴器联接的耦合转子系统模型。分析了耦联转子系统的临界转速、模态振型和不平衡响应,研究表明:
1) 考虑到弹性薄圆盘大变形的影响,分析了弹性膜盘联轴器刚度随位移的非线性表达式,采用线性和非线性模型描述,刚度相差为16.77%。
2) 外径厚度、内外直径比和中间轴长是影响膜盘联轴器刚度重要的结构参数,联轴器刚度随着外径厚度的增加而显著增加;轴向刚度、径向刚度和角向刚度随内外直径比的增大而增大,而扭转刚度变化不大;径向刚度、角向刚度和扭转刚度随着中间轴长增大而减小,轴向刚度基本不变。
3) 转子系统的临界转速提高了各单跨转子系统的临界转速,耦联转子系统的模态振型与各单跨转子系统的模态振型相关。
4) 采用联轴器联接的耦联转子系统,分析了联轴器对耦联转子系统的影响,发现联轴器刚度的增加会提高耦联转子系统的临界转速,同时角向刚度和径向刚度的增加也会使耦联转子系统的不平衡振动响应变得更加明显。

