一种求解TSP问题的改进鸟群算法
贺亦甲 符强 朱俊杰 许炜杰


摘 要: 针对组合优化的旅行商(Travelling salesman problem, TSP)问题,提出了一种基于改进鸟群算法的求解方法。制定了TSP路径编码方案,并利用鸟群的飞行行为、觅食行为和警惕行为实现TSP路径的优化搜索。同时结合模拟退火算子帮助鸟群在求解过程中跳出局部最优区域,并利用2-opt手段处理路径交叉情况,以提高局部搜索精度。最后進行了TSPLIB标准库测试算例的实验仿真,实验结果证明,与同类算法相比,改进鸟群算法具有更好的寻优能力。
关键词: TSP问题; 鸟群算法; 模拟退火算子; 2-opt
中图分类号:TP301.6 文献标志码:A 文章编号:1006-8228(2019)05-56-05
Abstract: Aiming at the problem of travelling salesman problem (TSP), a method based on improved bird swarm algorithm is proposed. The TSP path coding scheme is developed, and the optimal search of the TSP path is realized by using the bird's flight behavior, foraging behavior and vigilance behavior. At the same time, the simulated annealing operator is used to help the bird group jump out of the local optimal region in the solution process, and the 2-opt method is used to process the path intersection to improve the local search accuracy. The experimental simulation on the TSPLIB standard library test example shows that the improved bird swarm algorithm has better optimization ability compared with similar algorithms.
Key words: TSP problem; bird swarm algorithm; simulated annealing operator; 2-opt
0 引言
旅行商问题(TSP问题)又称货郎担问题。该问题描述的是由旅行商人拜访给定的城市,而每个城市必须经过且只能访问一次,最后回到第一次拜访的城市从而完成旅行,问:在此条件下如何得出所有可能路线中的最短路径。TSP问题作为组合优化领域内一个典型NP难题,被广泛应用于当代车辆路径规划,物流配送等方面。随着城市规模的扩大,TSP问题的复杂度会大幅度增加,导致求解时所需计算量与计算时间呈指数型增长。因此,传统方法如枚举法等已经难以应对此类问题。目前,在求解TSP问题的诸多方法中,效果较为突出的是群智能算法,如遗传算法(Genetic Algorithm,GA)[1],粒子群算法(Particle Swarm Optimization,PSO)[2]以及其他同类群智能算法[3~5]。群智能算法在处理大规模问题时,可以快速搜索到TSP问题的近似解,是求解TSP问题的有效途径。
鸟群算法[6](Bird Swam Algorithm,BSA)是Meng Xian-Bing等人近年提出的一种新型群智能算法,该算法利用鸟群的飞行行为,觅食行为以及警惕行为等实现位置更新及信息传递,并迭代靠近目标解。由于其具有收敛精度高,鲁棒性强的特点,因此受到了不少学者的关注,并被广泛应用于各个领域,如微电网优化[7],神经网络[8]等。
当城市规模较大时,BSA算法在求解TSP问题时易出现早熟收敛。本文针对该问题,设计了一种改进鸟群算法(Improved Bird swarm algorithm,IBSA)解决TSP问题的方案。将BSA算法与模拟退火算子[9]相结合,扩大算法的全局搜索能力,加强求解的精确性与稳定性。最后,分别将IBSA算法,BSA算法,GA算法以及PSO算法对TSPLIB标准数据进行测试,并将各算法的实验结果进行对比,以验证本文提出算法的有效性。
1 BSA算法简介
BSA算法通过模拟鸟群的飞行行为、觅食行为,以及警惕行为进行位置变换,分析这些行为的规律得到问题的最优解。假设规模为N的鸟群在D维空间飞行, 记第i只鸟在t时刻的位置为:,则三种行为可具体描述如下:
1.1 觅食行为
当判断鸟群进行觅食行为时,立刻记录和更新鸟群的个体以及种群的最优觅食经验,并将这个经验及时通过传递信息,共享给所有种群。觅食行为位置更新公式如下:
其中,rand(0,1)是0到1之间均匀分布的随机数,C是认知系数,S是社会系数,Pi,j是当前迭代中这只鸟的早前最优位置,gi是群体的早前最优位置。
1.2 警惕行为
当鸟群进入警惕行为时,每一只鸟开始尝试靠近种群中心,其中具有更高警惕性的鸟则更容易靠近种群中心。警惕行为位置更新公式如下:
其中,k(k≠i)是在[1,N]之间的一个随机正整数,rand(0,1)是0到1之间均匀分布的随机数,rand(-1,1)是-1到1之间均匀分布的随机数,,pFiti是种群中第i只鸟的最佳适应值,sumFit是种群最佳适应值总和,ε是计算机生成的最小常数,meanj是所有种群中第j维平均位置。
1.3 飞行行为
鸟群会周期性飞往其他的地域,到达此地域时,鸟群将会根据自身寻找食物的能力在生产者和乞讨者之间分出界限。能力高的鸟为生产者,能力低的鸟的为乞讨者,剩下的鸟随机分为生产者或者乞讨者。生产者积极进行觅食行为,乞讨者随机选择一个生产者跟随进行觅食。飞行行为位置更新公式如下:
其中,公式⑶是生产者的位置更新公式,公式4是乞讨者的位置更新公式。randn(0,1)是服从标准正态分布的随机数,rand(0,1)是0到1之间均匀分布的随机数,k∈[1,2,3,…,N],FL表示跟随系数。
2 求解TSP问题的IBSA算法
2.1 TSP问题中的路径编码
为设计IBSA算法求解TSP问题的方案,本文引入了交换序方法来实现位置更新。令为交换运算符,则式子XY表示交换序X以概率Y保留,故对IBSA算法进行以下编码:
⑴ 种群初始化,生成一个种群数为i,城市数为j的城市集合xi,j,第t代路径定义为。
⑵ 觅食行为重新定义为以下公式:
表示当前路径,表示更新后的路径。表示基本交换序以的概率保留,表示基本交换序以的概率保留。
⑶ 警惕行为重新定义为以下公式:
表示当前路径,表示更新后的路径。表示基本交换序以的概率保留,表示基本交换序以的概率保留。
⑷ 飞行行为重新定义为以下公式:
表示当前路径,表示更新后的路径。表示以的概率保留,表示基本交换序以的概率保留。
2.2 2-opt算子
2-opt是一种局部优化算法,在求解TSP问题的应用如下:对当前最优路径R(假设是A->B->C->D->E->F->G),用穷举法搜索路径R中所有不相连两个节点的情况,每一次将两个节点之间的路径翻转过来获得新路径,如选中了B节点和E节点,则新路径为A->(E->D->C->B)->F->G,()部分为被翻转的路径。设生成的新路径为R1,如果R1路径长度比R路径长度短,则保留R1,接下来对R1进行B节点和F节点的选择,以此类推,不断保留更优的路径,直到处理完所有的情况。
2.3 模拟退火算子
模拟退火算法的原理来源于固体退火的过程。固体在温度高时,粒子不稳定且无序,此时容易接受最差解从而跳出局部最优,然后在降温的过程中粒子逐渐变得有序稳定。在降温过程中重复着“产生一个新解→判断是否接受→多次迭代→降温”的過程。
本文对某一条路径用模拟退火算子优化方法如下:
Step1 初始化参数,设定初始温度T,退火速度系数A,迭代次数M,终止温度Tf。
Step2 通过一定的扰动方式更新路径R,生成新的路径R1。
Step3 比较R和R1的路径长度,如果R1长度更短则保留R1,否则以的概率保留R1。最后,令,达到降温的目的。
Step4 判断T是否达到终止温度Tf,达到则给出优化结束后的路径,否则转回step2。
模拟退火算子具有较好的全局搜索能力,能更好地协助改进鸟群算法通过对最优解进行搜索寻优。如果搜索到更优解,则更新最优解,否则不更新。
2.4 基于IBSA算法的TSP问题求解流程
BSA算法虽然可以有效地求解TSP问题,但是在求解时容易出现过早收敛,影响解的精度。IBSA算法通过引入模拟退火算子,来增强全局搜索能力,避免陷入局部最优,有效的提升了解的精确性。结合以上对BSA算法的改进,基于BSA算法的TSP问题求解步骤可描述如下。
步骤1 初始化城市,使城市数为N,种群数为pop,两两城市距离为Di,j,迭代次数为T,并计算初始种群路径长度。
步骤2 记录鸟群的初始全局最优路径,全局最优路径长度,个体最优路径,个体最优路径长度。
步骤3 根据飞行间隔FQ判断是否飞行,若飞行,则区分生产者与乞讨者。若不飞行,则区分觅食行为与警惕行为。
⑴ 进行觅食行为更新路径,并更新种群路径长度。
⑵ 进行警惕行为更新路径,并更新种群路径长度。
⑶ 进行飞行行为更新路径,其中生产者积极寻找新食物,乞讨者跟随生产者进行觅食,并更新种群路径长度。
步骤4 在通过觅食行为,警惕行为,飞行行为更新出的pop条路径中,引入变异,从而增加种群的多样性,并更新种群路径长度。
步骤5 对当前最优路径用2-opt算子进行局部更新,并更新种群路径长度。
步骤6 对当前最优路径用模拟退火算子更新,并更新种群路径长度。
步骤7 更新全局最优路径,全局最优路径长度,个体最优路径,个体最优路径长度。
步骤8 判断是否完成迭代次数,若未完成,则跳转到步骤3,若完成,则跳到步骤9。
步骤9 终止算法,输出最优路径。
3 实验仿真与分析
实验仿真的环境是在Window 10系统core i5的环境下进行,测试平台为MATLAB R017b。以下是本文各测试算法的参数。GA算法中,种群个数为100,交叉概率为0.8,变异概率为0.2。PSO算法中,微粒数为100,个体经验保留率为0.25,全局经验保留率为0.25。BSA算法及IBSA算法中,鸟群种群个数为100,认知系数为0.25,社会系数为0.25。
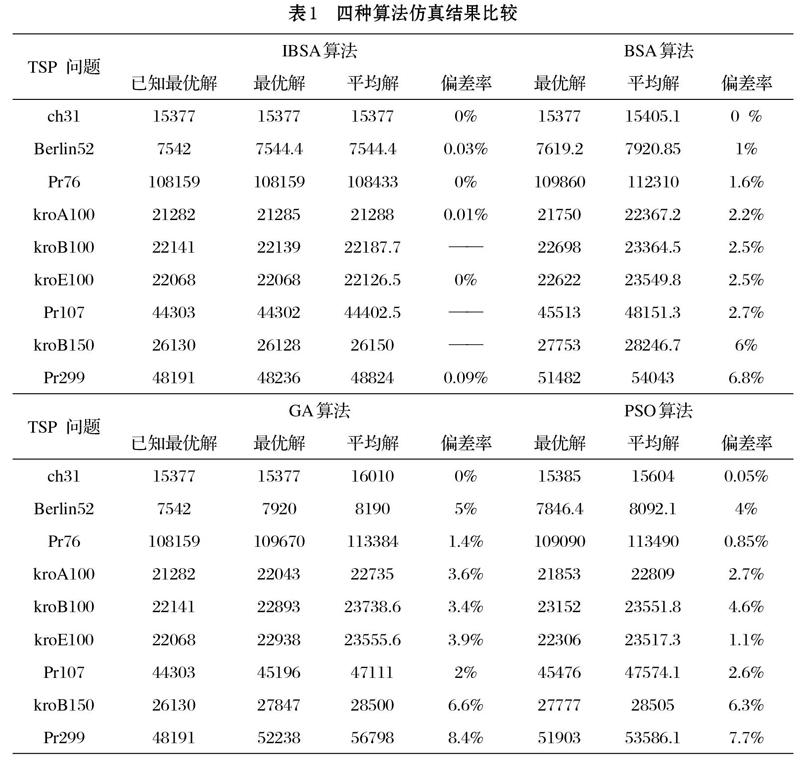
为了验证IBSA算法求解TSP问题上具有优秀的性能,我们随机抽取了TSPLIB标准库中九组不同规模的测试数据,每组数据分别利用IBSA算法,BSA算法[6], GA算法[1]和PSO算法[2]进行求解。为公平起见,每种算法均加入2-opt算子,并迭代1000次。同时,为了验证算法的鲁棒性,将每组数据用不同算法测试10遍,分别记录他们的最优解,最差解与平均值,并计算不同算法得到的最优解偏差率,不同算法之间进行对比分析。结果如表1所示。
表1的实验结果表明,BSA算法的最优解和平均解与PSO算法,GA算法偏差不大,甚至有时候BSA算法可以寻找到更优的解,这证明了BSA算法可以有效求解TSP问题。但是从适应度收敛曲线可以看出,当城市规模增大时,BSA算法容易早熟收敛,无法准确搜索到更精确的解。
本文设计的IBSA算法在求解ch31,eil76这些小规模城市问题时,均可搜索到与已知最优解一致的路径。并且在针对较大规模问题时,IBSA算法搜索到最优解的偏差率均在0.09%以下。对于kroB100,pr107,kroB150问题,IBSA算法甚至得出了比已知的最优解更精确的结果。另外,从多次计算的平均值可以看出,IBSA算法的平均值和最优解的偏差相对其他算法更小,证明了IBSA算法具有较强的鲁棒性与稳定性。
为了更好展现IBSA算法的求解性能,记录并绘制了各TSP测试结果的最佳路径图以及各对比算法适应度收敛曲线。因篇幅限制,图1仅显示berlin52、pr76的测试结果
图1表明,与BSA算法、GA算法和PSO算法相比,IBSA算法不但能够获取更优的路径解,而且具有明显较快的搜索速度,在较少的迭代次数中即能捕获最好的目标解。
4 结论
BSA算法在求解小规模TSP问题时具有良好的收敛精度与稳定性,并为进一步提高在问题规模扩大时算法求解的精确性,然而在问题规模扩大时容易陷入局部最优现象。本文提出了一种基于IBSA算法的TSP问题解决方案。在BSA算法中加入模拟退火算子以提高算法的全局搜索能力,进一步提高最优解的质量,并通过2-opt手段解决路径交叉的问题。实验结论证明,从平均值与最优解看,IBSA算法相对BSA算法、GA算法和PSO算法,无论是路径解的精确性还是每次搜索结果的稳定性都有较大的提高。从偏差率看,IBSA算法也极为接近最优解。因而本文提出的IBSA算法在求解TSP问题上的搜索最优解能力上面具有较强竞争力。
参考文献(References):
[1] 邓慧允,张清泉.蚁群算法与遗传算法在TSP中的对比研究[J].山西师范大学学报(自然科学版),2017(3):34-37
[2] 裴皓晨,娄渊胜,叶枫等.一种求解旅行商问题的改进混合粒子群算法[J].计算机与数字工程,2018.46(2):218-221
[3] 杨进,郑允,马良.改进的猫群算法求解TSP[J].计算机应用研究,2017.34(12):3607-3610
[4] 张子成,韩伟.求解TSP问题的自适应离散型布谷鸟算法[J].计算机工程与应用,2017.10:48-54
[5] 吴虎胜,张凤鸣,李浩等.求解TSP问题的离散狼群算法[J].控制与决策,2015.10:1861-1867
[6] Meng X B, Gao X Z, Lu L, et al. A new bio-inspired optimisation algorithm: Bird Swarm Algorithm[J]. Journal of Experimental & Theoretical Artificial Intelligence,2016.28(4):673-687
[7] 曾嶒,彭春華,王奎等.基于鸟群算法的微电网多目标运行优化[J].电力系统保护与控制,2016.44(13):117-122
[8] 郭彤颖,陈露.基于鸟群算法优化BP神经网络的热舒适度预测[J].计算机系统应用,2018.4.
[9] 徐胜,马小军,钱海等.基于遗传-模拟退火的蚁群算法求解TSP问题[J].计算机测量与控制,2016.24(3):143-144

