一种低时延的极化码设计方法

黄志亮 张施怡 周水红

摘  要： 提出一种基于修改的连续消去（MSC）译码算法的极化码时延降低方法。在MSC译码算法中，可以降低类型-I和类型-II节点的时延。通过重新分配信息位，所提出的方法可以获得一种较好的类型-I和类型-II节点的分布，在MSC译码算法下可以进一步降低译码时延。仿真结果表明，在与原算法的译码性能相比可忽略的损失下，由该方法构造的极化码可以达到8.5%的时延降低。而且，该方法易于调整差错性能与译码时延之间的权衡。

关键词： 极化码; 修改的连续消去译码算法; 时延降低

中图分类号：TN911.2          文献标志码：A     文章编号：1006-8228（2019）05-19-04

Abstract： A latency reduced method is proposed based on Modified Successive Cancellation （MSC） decoder for decoding polar codes. In the MSC decoder， it is shown that latencies for both the rate-zero and the rate-one nodes can be reduced. By redistributing the information bits， the proposed method can obtain a good rate-zero and rate-one nodes distribution， in which decoding latency can be further reduced with MSC decoder. Simulation results show that the new polar code （obtained by the proposed method） achieves 8.5% latency reduction with neglected error performance loss compared with the original polar code. Furthermore， it is easy to adjust the trade-off between the error performance and decoding latency by the proposed method.

Key words： polar code; modified successive cancellation decoder; latency reduction

0 引言

近年來，由于极化码[1]是第一种渐近性能达到香农限，同时有着低编译码复杂度，并且能广泛适用于各种不同信道场景的信道编码方案，从而引起了人们广泛的关注。虽然极化码有着丰富和完善的理论，但其在实际应用中还存在着一些问题需要解决。由于连续译码的特性，传统的连续消去（SC）译码产生一个很高的时延。文献[2]表明了一个类型-II节点（稍后介绍）的时延可以降低为一个类型-I的节点，从而明显地降低了译码时延，并且没有损失译码性能。对于一个具有固定码长的极化码，类型-I和类型-II节点的分布是由信息位集合确定的。我们提出一种对原始信息位集合进行微调的方法，以获得一种具有较好的类型-I和类型-II节点的分布的新的信息位集合，进而降低译码时延，并且与原始的信息位集合相比，具有较小的性能损失。

1 准备工作

1.1 极化码

极化码将N个独立的二进制输入离散无记忆（B-DM）信道W转化为其他N个B-DM位信道。构造一个N维的极化码是等价于寻找K个最好的位信道。在文献[1]中，最好的位信道是有着最小的巴氏参数，而在文献[3]中则是在最大似然（ML）译码下有着最小的误码率。在本文中，使用误码率评估位信道的好坏。然后，一个极化编码方案是由三个参数唯一确定：码长N，码率R=K/N和一个由K个最好的位信道构成的信息位集合A。一个极化编码方案仅仅传输K个最好的位信道和令N-K个位是已知的对于发送方和接收方。属于集合A的位称为信息位，属于集合[N]＼A（[N]={1，…，N}）的位是称为冻结位（在本文中冻结位是全0）。

1.2 修改的连续消去译码算法的简要回顾

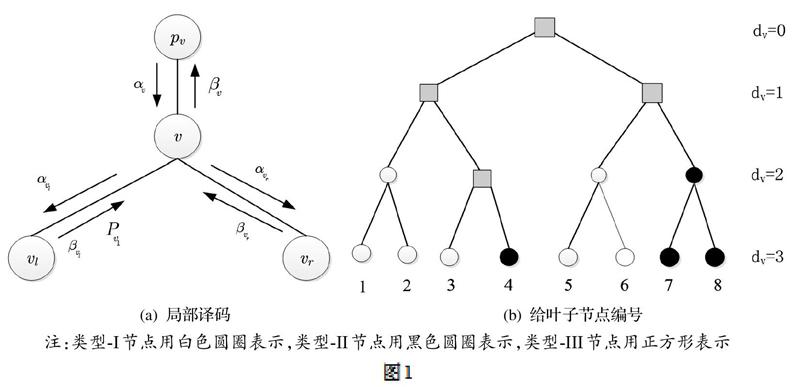
对于m>0，令Tm表示深度为m的完全二叉树。因此，Tm有N=2m个叶子。一般方式下，树的叶子节点的索引集为[N]，正如图1（b）中m=3，使用这棵树可以从顶部到底端执行SC译码[2]。

给定一个节点v∈Tm，令Vv表示根节点为v的子树和Iv表示所有叶子节点是节点v的后代构成的索引集。令A?[N]是一个极化码的信息位集合，如果Iv?A，那么我们称在Tm上的一个节点v是类型-II节点。类似地，如果，则我们称在Tm上的一个，节点v是类型-I节点。

给定一个节点v，分别用dv、pv、vl和vr表示它的深度、父节点和左、右节点;见图1（a）。对于每个节点v，有一个实向量αv和一个长度为的二进制数向量βv。如图1（a）所示，当激活一个非叶子节点v时，它立即由计算αv，然后激活vl并立即由αv计算。在执行完节点的过程后，将传递到v。紧接着，激活节点vr和它立即由αv和计算。在执行完节点的过程后，将传递到v。那么局部译码器根据和计算。在这点上，在节点v的局部译码器的操作终止。对于一个非冻结叶子节点，βv是由αv决定;对于一个冻结节点，βv直接设置为0。

SC译码程序是开始于根节点vroot，其中实向量是由接收信道输出获得。通过局部译码器和对叶子节点的处理，向量αv和βv是被计算对于每个节点v。对Tm上的叶子节点执行判决。由于篇幅所限，本文不作评述，可以参考文献[2]中对于一棵完全二叉树上的SC译码过程。

在文献[2]中，引入了一种对SC译码算法的修改，其中简化了类型-I和类型-II节点的操作。对于一个类型-I节点，它可以立即设置为全零向量而不用激活它的孩子节点，因为一个类型-I节点的后代都是类型-I节点。对于一个类型-II节点，可以同时译码其节点的索引集合Iv里的所有位，而且不需要激活它的孩子节点。他们称这种技术为修改的SC（MSC）译码算法。

1.3 给定的极化码在MSC译码下的时延评估

对于极化码而言，有许多影响时延计算的因素。为了使问题更清晰，我们假定：①一旦激活一个节点v时，它需要一个时钟计算αv同时使用个并行处理器;②忽略所有的二进制操作。

为了计算时延，基于以上的假设，需要考虑三种情况分别对应三种不同类型的节点。①对于一个类型-I节点，不需要假设，因此没有时延对于一个类型-I节点和没有激活这个节点的所有后代。②对于一个类型-II节点v，它需要一个时钟计算αv，并且在索引集合Iv的所有位仅仅需要译码二元操作符而不需要激活它的孩子节点。因此对于一个类型-II节点，它需要1個时延（一个时钟），并且将不会激活所有的后代。③对于类型-III节点，它需要1个时延（一个时钟）计算αv，并且将会连续激活它的左右孩子节点。首先，激活左孩子节点，然后，在处理完左孩子节点的子树后激活右孩子节点。注意根节点不会产生时延。

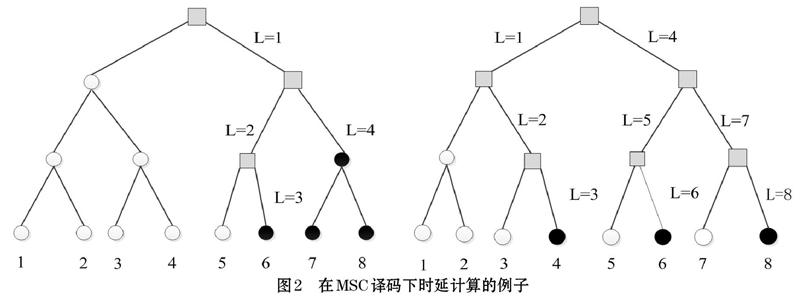
接下来，我们提供了一个例子解释图2中极化码的时延计算。如图2（a）所示，信息位集合是A1={6，7，8}，图2（b）中信息位集合是A2={4，6，8}。通过上述讨论，对应信息位集合A1和A2的极化码的时延（L）分别是4和8。

2 提出的方法

对于固定的码长N和码率R，大小为NR的集合[N]的任意子集（为了简便假定NR是一个整数）可以是一个信息位集合。每个信息位集合对应一种极化码和它们的时延互不相同。由K个最好的位信道构成的信息位集合A在MSC译码算法和所有可能的信息位集合下有最好的纠错性能。我们观察到，相邻位信道之间的差异是非常小的。因此，存在一个信息位集合B与由信息位集合A构成的极化码有类似的纠错性能，而在MSC译码算法下前者比后者有较小的时延是极其可能的。

更准确的说，基于一个阈值δ（δ>0），在第NR个较好的位信道（用误码率评估N个位信道）截止点附近选择一个小集合。然后信息位集合在S中重新分布，并且每一种在集合A＼S中的原始信息位的重新分布对应着一种信息位集合（和A具有相同的元素数目）。最后，在所有可能的信息位集合中挑选一个具有最小的时延的信息位集合。

在数学上，令Pe（i）表示第i层位信道的误码率。令As表示由A＼S中的信息位构成的集合。令表示一个n-元素集的r-组合数。那么可以将提出的方法描述如下。

输入：一个底层的B-DM信道，码长N和码率R。

输出：一个有着NR个元素个数的信息位集合B。

步骤1 用文献[3]的方法计算N个位信道的误码率和将这N个位信道按照升序排序。令n表示升序的映射关系。

步骤2 选择一个小集合S。对于1

步骤3 产生个信息位集合。对于，产生一个S的l-组合数并将它表示为Ei。那么可以将看成码长为N、码率为R的极化码的信息位集合。总共有个S的l-组合数。因此有个信息位集合。

步骤4 利用前一节的方法计算所有个信息集合的时延和选择具有最小时延的集合作为输出信息位集合B。

一般来说，中元素的个数是小的。因此利用我们的方法可以计算所有生成的个信息位集合的时延。

注意原始的信息位集合是由K个最好的位信道构成，而使用提出的方法所产生的信息位集合通常不是由K个最好的位信道构成。随着δ值的变大，挑选的个位信道的质量变得越差。因此，随着δ的变大，挑选的信息位集合（对应一种极化码）的译码性能越差。

3 仿真结果

考虑二进制相移键控（BPSK）调制和一个加性高斯白噪声（AWGN）信道。特别的，二进制码字c=（c1，…，cN）基于xn=1-2cn映射到一个传输序列x=（x1，…，xN）。在接收端，获得接收向量y=（y1，…，yN），其中yn=xn+vn，vn是独立同分布随机变量，它们都满足均值为0和方差为N0/2的高斯分布。

图3给出了不同δ的极化码利用系统编码方法[4]在MSC译码算法下的误码率和误帧率曲线。注意文献[4]中提出的系统编码方法比原始的非系统编码方法有着较优的译码性能。码长N=256，码率是1/2。利用文献[3]中的方法评估N个位信道。

图3展示了δ=0.02的极化码有8.5%（（106-97）/106?8.5%）的时延降低相比于原始的极化码（δ=0.0），并且二者在利用系统编码方法的MSC译码算法下具有几乎相同的译码性能。图 3 也表明了随着δ的增大，极化码的时延逐渐降低，并且译码性能损失随之相应的增加。因此通过调整δ，控制差错性能与译码时延间的权衡是容易的。

4 总结

本文提出了一种极化码在MSC译码算法下的差错性能与译码时延之间达到折衷的方法。引入了δ控制这种折衷。对于码长为256、码率为1/2的码，仿真结果表明当δ=0.02时，所提方法达到了8.5%的时延降低，并且有着可忽略的性能损失。而且，通过调整δ，控制差错性能与译码时延间的权衡是容易的。

参考文献（References）：

[1] Arikan E. Channel polarization： a method for constructing capacity-achieving codes for symmetric binary-input memoryless channels[J]. IEEE Trans. Inform. Theory，2009.55（7）：3051-3073

[2] Alamdar-Yazdi A， Kschischang F R. A simplifiedsuccessive-cancellation decoder for polar codes[J]. IEEE Commun. Lett.，2011.15（12）：1378-1380

[3] Tal I， Vardy A. How to construct polar codes[J]. IEEETrans. Inform. Theory，2013.59（10）：6562-6582

[4] Arikan E. Systematic polar coding[J].IEEE Commun. Lett.，2011.15（8）：860-862