无绝缘轨道电路长度的建模研究

杨骞

摘   要：无绝缘轨道电路数学模型的建立，可以决定补偿式和无补偿式JTC的分路灵敏度。在不同JTC参数值的条件下，由数学模型获得的分路灵敏度的大小和分布被列举出来，并定义了最差分路灵敏度的点。由此文章提出一个允许范围内的轨道电路长度的标准，基于这些标准，可得到JTC的最大长度。

关键词：无绝缘;轨道电路;分路灵敏度

轨道电路机械绝缘节已被证明是高速铁路运输的障碍之一，同时也是很多事故发生的主因。为了克服这些不利因素，无绝缘轨道电路（Jointless Track Circuit，JTC）被提出来。起初较短长度的JTC用于平交道口的控制[1]。后来JTC运用于自动闭塞制式的区间和列车自动运行控制系统。现在几乎所有的信号设备供应商都生产了自己的无绝缘轨道电路。

但JTC存在一个关于长度的主要问题：为了增加长度，采用中央供电，两端接收的方式，通过在两轨间增加电容，实现对钢轨阻抗的周期性校准[2]。

为了证明这些方法的必要性，也为了判断对轨道电路长度的影响，提出了无绝缘轨道电路最大长度的说法。这些问题被由分立元器件组成的实验室电路模型通过实验方式解决。尽管实验室模型仅对轨道线路参数进行仿真，但获得的数据结果已经很接近现场实际应用。多种仿真方式被采用于此项研究中，它们对于以多点传输系统来研究轨道电路参数极为有利，但在将轨道电路作为线性传感器研究时却呈现出糟糕的适应性。在有关JTC的问题研究中，部分使用二端口网络模型的建模研究方式，但完整性较差，且缺少明确可用的结果。本文客观展示了一个改进后的JTC二端口网络模型，用来分析JTC分路灵敏度和最大适用长度。

1    JTC的数学模型

大多数JTC可由图1模型表示，Zinp.t和Zinp.r分别是发送端和接收端设备的输入阻抗。不同种类无绝缘轨道电路的区别在于电气绝缘节（Electric Separation Joint，ESJ）的设置和电气绝缘节处的线路长度。此次建模研究中，设ESJ代替了轨道电路端口置于送电端的左侧。两钢轨在距离发送端左侧l处紧密连接，电容Cj为了补偿线性输入阻抗的电感分量。ESJ2与ESJ1完全相同，对称地位于接收端的右侧。上述模型为UM71型JTC的基础模型，也可稍做改变用于其他的JTC中，线路中小轨道电路呈S连接形式这一特殊情况除外。

给出的模型并没有额外考虑增加轨道电路长度的方式。上面提到过，补偿电容是用来补偿钢轨传输线性衰耗。每公里最佳补偿电容大小，其中，φz是钢轨阻抗的相角，ω是角频率。补偿电容容值和补偿间距ΔL在各种JTC中都不同，由于的前提条件是，钢轨衰耗最小并要求忽略补偿电容对轨道电路分路灵敏度的影响，故加深对补偿电容影响的研究就更有必要[5]。

为了证明补偿电容的影响，建立了复杂轨道电路模型，如图3所示。将钢轨线路等效于n个互相链接的二端口网络模型，每个模型中间位置设置补偿电容C。当车辆出现在第i个链中时，参数Ash，Bsh，Csh，Dsh可以作为二端口网络的参数，通过矩阵计算而得：分别为分路链前i-1个链，本身分路的链，和分路链后n-i个链。

2    JTC最大长度计算

轨道电路既能在主轨道区段检测列车分路，又在绝缘节区段检测的能力是最大JTC长度的基础要求。所有对补偿式和无补偿JTC的报告结果都显示绝缘节区段的灵敏度是最不利的条件：当轨道电路长度增加，灵敏度降低。这些关系即是通过计算决定最大JTC长度的基础。

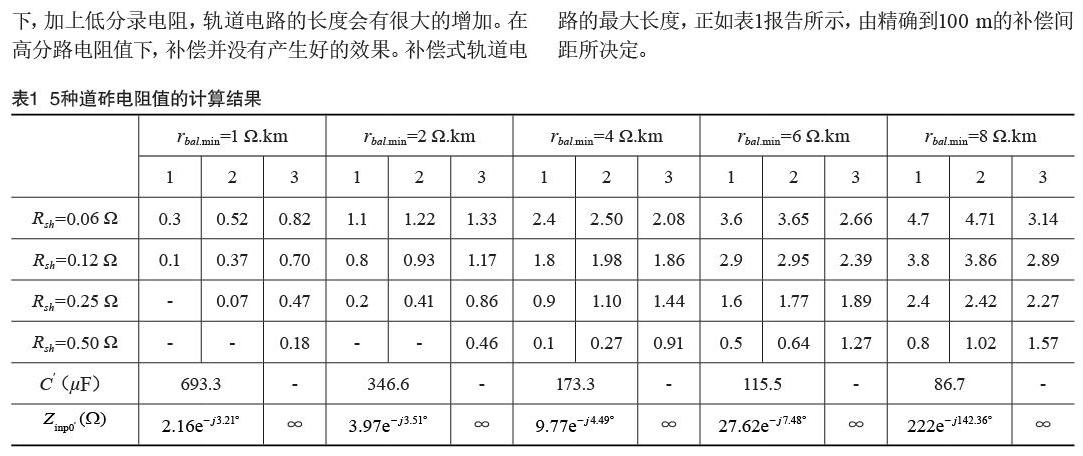
曲线1补偿式JTC，曲线2分散补偿式JTC，曲线3无补偿式JTC在5种道砟电阻值下进行计算，每个值决定了补偿电容C'和轨端输入阻抗Zinp0，结果如表1所示。可以得出以下结论。

（1）最大JTC长度由最小道砟电阻和列车分路电阻决定。

（2）对于rbal.min=2 Ω.km的轨道线路，就像欧洲标准那样，无补偿式轨道电路的最大长度大于补偿式轨道电路，介于此因，补偿电容仅可用于减小衰耗。

（3）关于轨道电路长度，在高rbal.min值下，补偿是有效的。此由高速线路提供，其rbal.min值大于8 Ω.km。在此情况下，加上低分录电阻，轨道电路的长度会有很大的增加。在高分路电阻值下，補偿并没有产生好的效果。补偿式轨道电路的最大长度，正如表1报告所示，由精确到100 m的补偿间距所决定。

3    结语

本研究表明了一个可用的JTC长度的重要增加方法，需要做的是保持最小道砟电阻值尽可能的大。轨道电路的高衰耗率可以运用级联补偿电容的方式来减小。在高道砟电阻情况下，电容会使轨道电路长度增加。当补偿电容值确定下来，最小道砟电阻值需要被确定下来，并要满足海维塞德条件。对于每个rbal.min值，轨道电路存在一个轨端最佳输入阻抗值。补偿电容之间的补偿间距不能小于100 m。

[参考文献]

[1]VILDER D E.Train detection system[J].European Railway Signalling，1995（6）：121-142.

[2]SHARIKOV V A，LIST F D.Level crossing with electronic track circuits[M].Moscow：Transport，1967.

[3]BRILEEV A M，CRAVTZOV U A，SHISHLIAKOV A V.Theory design and operation of track circuits[M].Moscow：Transport，1978.

[4]NENOV I，NEDELCHEV N，HILL R J.Railway track circuit optimization using two-port network analysis[C].Poland：Proceedings of Second International Conference on Modern Supply Systems and Drives for Electric Traction，1995.

[5]HILL R J，CARPENTER D C，TASAR T.Railway track admittance，earth-leakage effects and track circuit operation.[C].Philadelphia：IEEE/ASME Railroad Conference，1989.