基于生本取向小学数学习题教学方法运用的研究

摘 要:有的老师把练习课当成“习题课”,当成是知识点的简单累加。可想而知,这样的课堂教学效率将大打折扣。文章试图从运用教学方法的角度入手,从“教习题”的教学研究真正走向“用习题教”的教学研究。
关键词:生本取向;数学习题;教学方法
一、忽视生本取向是练习有效教学现状的弊端
现状一:雾里看花——练习目标不明确
【课堂观察】《排列与组合》。选用“2件衣服与3条裤子搭配——3种饮料与3种早点搭配——用1、2、3组成不同的两位数——用A、B、C三位同学排成一排,用几种不同的排法——路线图”等情境展开教学。
数学生活化的关键在于构建与学生生活经验相联系的数学问题。教师的关键在于是否善于整合生活中的数学实例,为课堂教学服务。对于过多情境包装的“华丽”课堂,所有学生是否都能理解教师的“用意”?
现状二:就题论题——教学内容无拓展
【课堂观察】四年级《封闭图形中的植树问题》。教师先是呈现:每边放4颗,一个正方形至少可以放几颗?学生尝试计算,在多样化的算法展示中,教师及时总结。之后,教师及时提炼出解决“方阵问题”的一般方法。殊不知,本节课缺乏对于“植树问题”的沟通,没有及时地渗透一一对应思想。
一些数学老师,在教学时急功近利,过早提炼数学模型,让多数学生只记得总结性的规律,却不知其所以然。这就会导致学生与教师不能同步,错位建构概念。
现状三:一家之言——教学方法太单一
【课堂观察】六年级《鸡兔同笼问题》。有位教师是这样设计的:先出示内容,然后引导学生思考解决这个问题的方法。当学生说出列表法、假设法等方法后,教师顺势引出:从刚才的过程中你是怎样用发现假设法解决问题的?能说一说计算方法吗?大部分学生不知该怎么回答,教师便匆匆做了总结。学生缺少了理解的过程,体验与感悟不充分,只能在模仿中学习。
新课程改革实施以来,我们的教学呈现方式体现多样化。但是我们不得不反思,我们是怎么解决这个问题的?主要过程的呈现是否有利于困难生的理解与掌握?等等。
二、习题教学方法运用策略
1.改编素材——演绎新问题
(1)改数据。[对比案例分析](改进前):(四年级下册《植树问题》)同学们在全长100米的小路上一边植树,每隔5米栽一棵,(两端都栽)。一共需要多少棵树苗?
(改进后)全长100米改为1000米。
[分析]本例有意加深难度,把习题的数据改成更大了,将原课本100米换成了1000米。放手让学生尝试练习时,得到三种不同的答案。再把这个规律推广,渗透化繁为简的方法。
(2)补素材。教材提供的材料是这样的:
常规处理:三年级上册《搭配问题》中,我们在教学时这样处理:让学生利用教材当中的材料(3件上衣,2条裤子),通过画一画、连一连等操作,得到6种不同的搭配。
小组交流:通过刚才的练习你能明白什么?
[分析]学会以“一”变“多”:以衣服与裤子搭配为基点,从数量变化中理解搭配方法的不变,再从衣服与裤子的材料中进行适当扩展,运用列举、讨论的方式再一次产生更多的学习素材。开发学习材料前,教师要提前吃透教材提供的学习材料,结合本班学生生活实际,开发有联系、有对比的学习材料,变单一型学习材料为复合型学习材料。
(3)换题材。四上《田忌赛马》一课,对本课的教学题材做如下调整。
材料一:红牌(10、7、4)黑牌(3、2、1),双方实力悬殊,胜负分明。材料二:红牌(10、7、4)黑牌(9、6、3)。材料三:在材料二的基础上把黑牌换小。黑方实力稍遜,以弱胜强。材料四:红牌(10、7、4)黑牌(10、7、4),双方实力对等,以弱胜强。
[分析]了解原素材的弊端,突出主题:本例以玩牌游戏引入,激发学生的学习兴趣,调动学生探究的积极性。同时,有意渲染“选牌大的占优势”,引起学生认知冲突,引出选牌小的一定会输吗?激发学生进一步探究的欲望。
2.合理呈现——凸现问题本质
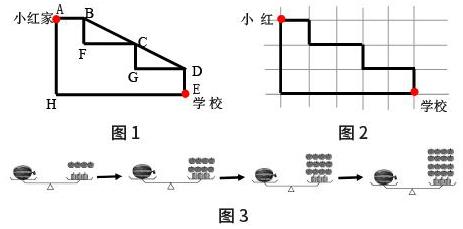
(1)动态呈现。从小红家到学校有下面的几条路可以走(如图1)。你觉得哪条路近?哪条路远吗?
学生一致认为(5条路中)走ABCDE是最近的,但在剩下的线路中,很多的学生认为ABFCGDE(暂且用字母表示)是最远,有少部分学生认为这条路跟AHE是一样长的,相持不下。
[改进策略]
第一步:隐去BCD路线;(还是有很多学生不理解);第二步:附上格子图(如图2);第三步:水到渠成。
[分析]能体现过程性展示:借助动态演示,打破思维定式。随着格子图的出现,更多的孩子想到了“转化”的方法,利用长方形的特点进行判断,学生充分体验了解决问题的全过程。
(2)互动呈现。交流也需要体现教师为主导,学生为主体的思想,在学生真正需要的时候交流。当教学《等量代换》的过程中,呈现:一个西瓜的重量=4个砝码的重量,一个砝码的重量=4个苹果的重量后,学生得出:一个西瓜的重量=16个苹果的重量(如图3)。
[分析]增强互动生成:怎样体现这一过程呢?关键是用砝码的重量为替换物。怎样替换?在师生的交换中,让学生上台操作,边演示边引导学生说理,充分理解替换过程。教师引导学生主体参与、互动、合作共同完成,而不是老师单方面“唱独角戏”,答案由学生自己去创造。这在某种程度上可以减缓学生心理依赖性。
(3)教师示范。一个长方形的周长是10米,它的长是3米,长方形的宽是多少?
学生可能会出现:①10÷2-3=2(厘米)或②(10-3×2)÷2=2(厘米),学生会利用长方形的特征和之前建立的表象,解释算式所要表达的意思,之后出现(如图4)验证学生的解题思路,在修正中不断完善知识。
[分析]帮助学生准确理解内容:在黑板上画了简笔画(如图4),直观地表达了过程,并配以算式,很好地进行了图式之间的沟通。每堂课尽可能地将重点处、难点处、关键处以简笔画、算式、表格等形式在板书上呈现,这能起到事半功倍的效果。
参考文献:
[1]郑毓信.数学思维与数学方法论[M].成都:四川教育出版社,2001.
[2]高宏.谈数学思维与数学方法论的教学意义[J].现代技能开发,2003(3):74.
作者简介:钟春林(1984—),男,浙江杭州人,小学一级教师,在职硕士。

