基于微分博弈的无线传感器网络恶意程序传播模型*
周海平,沈士根,冯 晟,黄龙军,彭 华
(绍兴文理学院计算机科学与工程系,绍兴 312000)
无线传感器网络WSNs(Wireless Sensor Networks)是由大量具有无线通信和感知能力的传感器节点组成的分布式通信系统。由于WSNs集感知、计算、通信等功能于一体,且价格便宜、部署方便,目前已经在农业、军事、工业制造等众多领域中得到了应用[1-4]。然而,由于WSNs中的传感器节点采用无线方式通信,且携带的电池能量有限,很容易受到恶意攻击[5-7],常见的攻击方式有信道干扰[8]、拒绝式服务DoS(Denial of Service)攻击[9]、身份欺骗[10]、恶意程序传播[11]等多种形式。相比其他攻击方式,恶意程序传播是一种影响范围更大、破坏力更强的攻击方式,因为传感器节点一旦被恶意程序感染,又会向其他节点传播恶意程序,导致整个网络迅速瘫痪[12-14]。
至今为止,人们已经对WSNs的入侵检测问题[15-16]和计算机网络中的病毒传播问题[17-18]做了大量研究,并取得了丰硕的成果,然而,对WSNs中恶意程序传播问题的研究目前仍处于初级阶段。与本文相关的研究成果包括:王小明等人利用元胞自动机方法对移动无线传感器网络中的恶意数据包传播行为进行模拟[19],揭示了不确定环境下恶意数据包传播的时空特征。文献[20]将传统的传染病传播理论应用于WSNs中的恶意程序传播过程,作者将恶意程序和入侵检测系统IDS(Intrusion Detection System)当做两种相互对抗的智能体,建立了二者之间的微分博弈模型,通过对博弈模型的分析和求解,得到了二者之间的均衡策略,该策略可以在抑制恶意程序的传播的同时降低检测代价。曹玉林等人将传染病模型应用于WSNs的病毒传播研究[21],他们将易感节点的免疫比例和感染节点的恢复比例做为最优控制变量,实现了最小成本开销下最大程度遏制病毒传播的目标。文献[22]对WSNs中的移动代理被攻击时病毒的传播行为进行了研究,发现在移动代理被攻击的情况下病毒更容易扩散。文献[23]提出了一个WSNs的蠕虫病毒传播模型,作者研究了通信半径和节点分布密度对病毒传播效果的影响。
尽管人们已经分别对WSNs中的攻防博弈模型以及恶意程序传播模型做过大量研究,但是目前这两方面的工作大多是独立开展的,而实际上,这两个领域的研究问题是紧密联系的。一方面,攻防双方所采取的博弈策略会影响恶意程序的传播结果。因为当恶意节点对合法节点发起攻击时,合法节点通常会采取一定的防御措施,这会影响恶意节点的攻击成功率,从而影响恶意程序的传播结果。另一方面,传播结果也会反过来改变攻防双方的博弈策略,这是因为博弈双方会根据网络中感染节点的比例来调整自己的策略。文献[24]用博弈论的方法分析了攻防双方的博弈策略,并依据博弈策略确定恶意程序的传播概率,从而建立了WSNs的恶意程序传播模型。然而,该文建立的博弈模型假定攻防双方都知道对方的节点类型,且攻防双方不会根据传播结果动态更新自己的策略,这显然与真实情况存在差异。实际情况中,恶意节点会伪装成合法节点,因此攻防双方不会知道对方的节点类型,此外,在恶意程序的传播过程中,两种节点的比例会发生变化,这会促使攻防双方及时调整自己的策略,因此,需要用微分博弈的理论来描述动态变化的博弈策略。基于以上分析,本文从攻防过程出发,建立了基于不完全信息的微分博弈模型,并将其与恶意程序传播模型耦合起来,从而探讨博弈策略对恶意程序传播结果的影响,并进一步揭示博弈参数与传播结果之间的关系,使人们有望通过控制博弈参数来抑制恶意程序的传播。
本文的研究框架如下:首先,建立WSNs中恶意节点与合法节点之间的攻防博弈模型,并对博弈策略进行分析与求解。其次,基于攻防双方的博弈策略建立WSNs的恶意程序传播模型,通过求解传播模型得到系统的实时感染比例与博弈参数之间的关系。再次,用数值模拟方法及元胞自动机模型对WSNs中的恶意程序传播过程进行模拟及仿真。最后,对数值模拟结果和元胞自动机仿真结果进行分析、比较及讨论。
1 WSNs中的不完全信息攻防博弈模型
在WSNs中,合法节点为了防御恶意节点的攻击,会启动入侵检测系统IDS(Intrusion Detection System)对收到的信息进行检测,但检测过程需要消耗一定的能量,由于无线传感器节点携带的电池能量十分有限,若每次收到信息时都进行检测,则很快会因能量耗尽而无法工作。考虑到其大多数情况下收到的都是正常信息,合法节点只需以一定的概率随机抽查一部分信息进行检测。同时,对恶意节点来说,若其频繁地发起攻击,则很容易被合法节点发现,为了掩饰自己的身份,恶意节点会经常发送正常信息(不攻击)。由此可见,恶意节点和合法节点在攻防博弈过程中会根据其所处的局势采取对自己最有利的策略。在博弈过程中信息发送方和信息接收方互不知道对方的身份,但是知道对方为合法节点及恶意节点的概率,因为在现实环境中,IDS会将每个时刻的检测情况上报给管理中心,然后管理中心会以广播的形式实时发布毒情报告(报告网络的感染节点比例),基于以上特点,本文采用不完全信息博弈模型对双方的攻防策略进行分析。
定义1WSNs中恶意节点与合法节点之间的不完全信息博弈模型可以表示为一个五元组Ξ=〈N,{Tj},p,{Sj},{uj}〉,其中:
①N为博弈参与者集合,对于本文来说,博弈在两个参与者之间进行,其中参与者1为信息发送者,参与者2为信息接收者,因此,N={信息发送者,信息接收者}。
②Tj为参与者j所属的类型空间,在WSNs中,传感器节点含有恶意节点和合法节点两种类型,因此,Tj={恶意节点,合法节点},j∈N。
③p为博弈参与者在类型空间上的概率分布,本文指恶意节点与合法节点所占的比例,该参数对所有参与者都是公开的。
④Sj为参与者j可采取的行动集合,该行动集合与参与者类型有关。本文中,当参与者为信息发送方且为恶意节点时,有“攻击”和“不攻击”两种行动,记为S发送者,恶意节点={攻击,不攻击};当参与者为信息接收方且为合法节点时,有“检测”和“不检测”两种行动,记为S接收者,合法节点={检测,不检测};当参与者为信息发送方且为合法节点时,只有“不攻击”一种行动,记为S发送者,合法节点={不攻击};当参与者为信息接收方且为恶意节点时,只有“不检测”一种行动,记为S接收者,恶意节点={不检测}。需要特别指出的是,其中的“不攻击”行动不是指节点不发送信息,而是指其发送的是正常信息。
⑤uj为参与者j在博弈过程中获得的收益,uj的值由所有博弈参与者的类型及策略组合决定。
表1给出了本文用到的一些符号的定义,表2给出了博弈双方的收益矩阵。

表1 符号定义

表2 合法节点与恶意节点的博弈收益函数表
在博弈模型中,信息发送方和信息接收方都含有恶意节点和合法节点,不论哪种节点,在发送信息(恶意程序或正常信息)时都需要消耗代价为eM的能量。合法节点对收到的信息进行检测需要消耗代价为eD的能量,当恶意节点向合法节点发起攻击,合法节点又正好进行检测时,合法节点会因成功检测出恶意程序而获得价值为a的收益,恶意节点则会因暴露身份而被修复,从而造成代价为a的损失。当恶意节点发起攻击,而合法节点不进行检测时,恶意节点会因成功传播恶意程序获得价值为b的收益,而合法节点则会因感染恶意程序造成代价为b的损失。另外,为了使博弈有意义,模型须满足a≥eD及b≥eM这两个条件。
另外值得指出的是,信息在WSNs的传递过程中可能需要经过多跳才能到达目的节点,但中间节点并不会参与博弈过程,因为中间节点为了节约能量一般只参与对数据的转发,而不会对转发的数据进行检测,数据转发之后会立即被中间节点删除,因此恶意程序也不会对中间节点造成影响,所以博弈只在信息的发起节点和目的节点之间进行。
由表2可知,作为信息发送方的合法节点和信息接收方的恶意节点都只有一种行动,不需要对它们的策略进行分析,因此本文只需要对信息发送方的恶意节点和信息接收方的合法节点的策略进行分析。合法节点在对收到的信息做出行动时,既要考虑对方的节点类型,也要考虑对方会采取哪种策略,若对方是恶意节点且发起攻击,则合法节点就应该进行检测,反之,就不应该检测;同理,若恶意节点面对的是合法节点,当对方开启检测,就不应该进行攻击,反之,就应该发起攻击。由此可见,恶意节点和合法节点之间的攻防博弈模型不存在纯策略纳什均衡解,下面从混合均衡策略的角度分析博弈双方的攻防行为。
定理1WSNs中恶意节点与合法节点之间的不完全信息博弈模型存在混合纳什均衡策略。
证明假设WSNs中合法节点的比例为s,恶意节点的比例为i,且两种节点发送信息的频率相同。另外,假设恶意节点以概率x进行攻击(传播恶意程序),以概率1-x不进行攻击(传播正常信息),合法节点以概率y进行检测,以概率1-y不进行检测,则根据收益矩阵,作为防御方的合法节点的期望收益Eus为:
EuS=ixy(a-eD)+i(1-x)y(-eD)+ix(1-y)(-b)+i(1-x)(1-y)·0+sy(-eD)+s(1-y)·0
(1)
作为攻击方的恶意节点的期望收益EuI为:
EuI=sxy(-a-eM)+s(1-x)y(-eM)+sx(1-y)(b-eM)+s(1-x)(1-y)(-eM)+ix(-eM)+i(1-x)(-eM)
(2)

ix(a-eD)+i(1-x)(-eD)-ix(-b)+s(-eD)=0
(3)
将s+i=1代入方程(3),整理得:
(4)
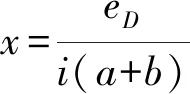
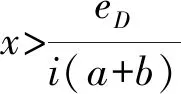


sy(-a-eM)-sy(-eM)+s(1-y)(b-eM)-s(1-y)(-eM)=0
(5)
整理上式得:
(6)


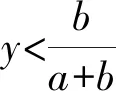


2 微分博弈驱动下的WSNs恶意程序传播模型
在WSNs中,当恶意节点向合法节点传播恶意程序时,若合法节点不进行检测,则会被恶意程序感染,感染后的节点变为恶意节点,并能进一步向其他节点传播恶意程序。反之,如果合法节点在遭受攻击时开启检测,则能阻止恶意程序的入侵并能清除恶意节点中的恶意程序,从而使恶意节点恢复为合法节点。假设WSNs中总共有N个节点,其中恶意节点个数为NI,占总节点数的比例为i,合法节点个数为NS,占总节点数的比例为s。每个恶意节点会在单位时间内随机选择一个其他节点发送信息,其中发送恶意程序的概率为x,发送正常信息的概率为1-x,合法节点会以概率y对收到的信息进行检测。根据上一节的分析,恶意节点与合法节点作为理性的智能体,会采用混合纳什均衡策略作为各自的攻防策略,即x=x*,y=y*,因此,单位时间内一个恶意节点成功感染一个合法节点的概率为x*(1-y*)s,而一个恶意节点被修复为合法节点的概率为x*y*s。于是单位时间内整个网络新增的恶意节点数为x*(1-y*)sNI,新增的合法节点数为x*y*sNI。WSNs中两种节点随时间的演化过程可以用微分方程组(7)表示:
(7)
方程组(7)两边同时除以N得:
(8)
于是有:
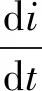
(9)
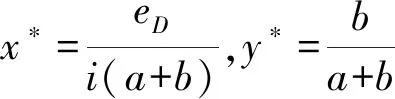
(10)
整理得:
(11)
令t0=0,并假设初始时刻的感染比例为i0,对方程(11)两边进行积分得:
(12)
即
(13)
整理得:
(14)
由式(14)可知,网络中恶意节点的感染比例与博弈模型中的收益参数有关,博弈参数决定了系统随时间的演化结果。
3 数值模拟与仿真
3.1 攻防策略与收益之间的关系数值模拟


图1 博弈双方策略的变化对合法节点期望收益的影响
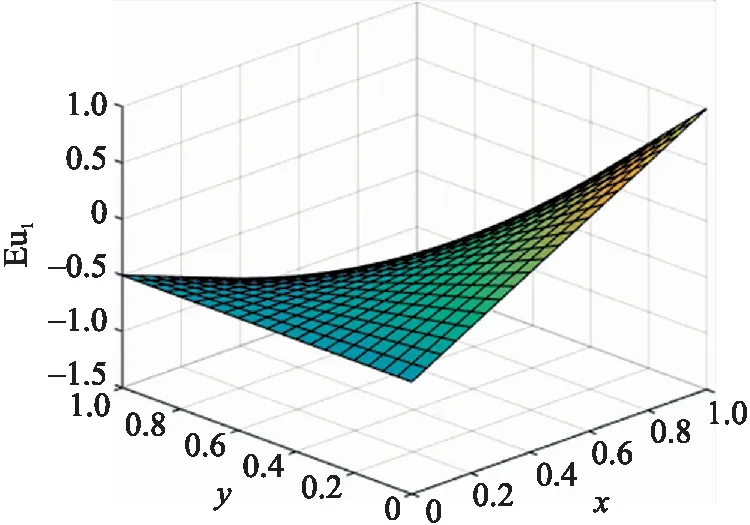
图2 博弈双方策略的变化对恶意节点期望收益的影响
3.2 恶意程序传播数值模拟
微分方程组(8)描述了WSNs恶意程序传播过程中网络节点状态随时间的演化行为,式(14)给出了该系统的解析解,对式(14)进行数值模拟,可得到网络中感染节点比例随时间的变化趋势,模拟结果如图3至图5所示,每张图中的四条曲线分别刻画了eD取不同值时系统的演化过程,从中可以看出博弈参数对传播结果的影响。
图3显示,当a>b时,随着时间的推移,网络中的节点感染比例逐渐达到1,最终所有节点都处于感染状态。此外,当eD增大时能加速恶意程序的传播,即合法节点的检测能耗越大,恶意程序的传播速度越快。解释如下:①当a>b时,x*(1-y*)si>x*y*si,即单位时间内新感染的节点多于恢复正常状态的节点,因此网络中的感染节点比例会不断增加,直至所有节点都被感染。②当检测能耗eD增大时,由混合纳什均衡策略可知,合法节点保持检测概率不变,而恶意节点提高了攻击概率,从而使恶意程序的传播速度变快。

图3 a>b时感染节点比例演化趋势(a=3.0,b=2.0)
图4显示,当a=b时,网络中感染节点的比例保持初始值不变。解释:当a=b时,x*(1-y*)si=x*y*si,即单位时间内新感染的节点数等于恢复正常状态的节点数,因此网络中的感染节点比例会保持不变。
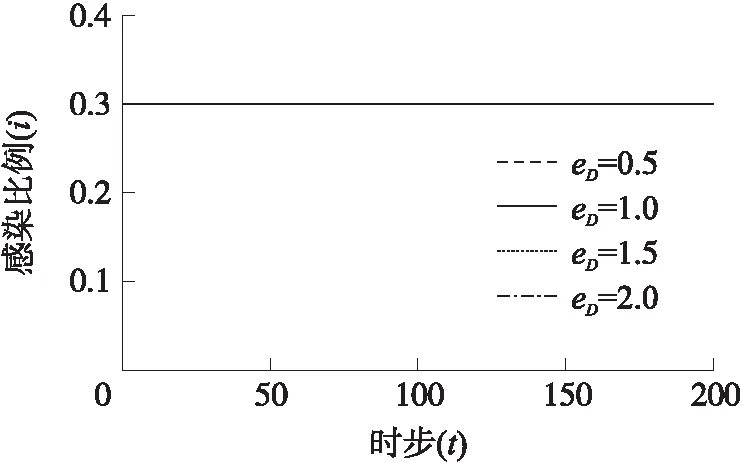
图4 a=b时感染节点比例演化趋势(a=2.0,b=2.0)
图5显示,当a
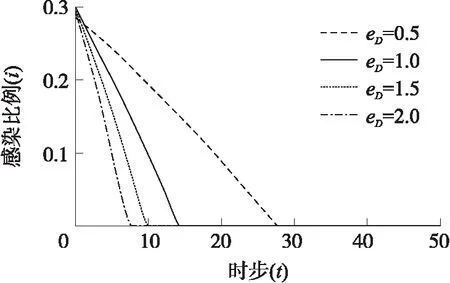
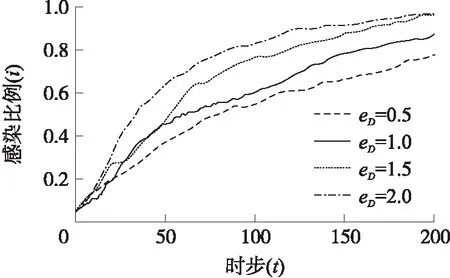
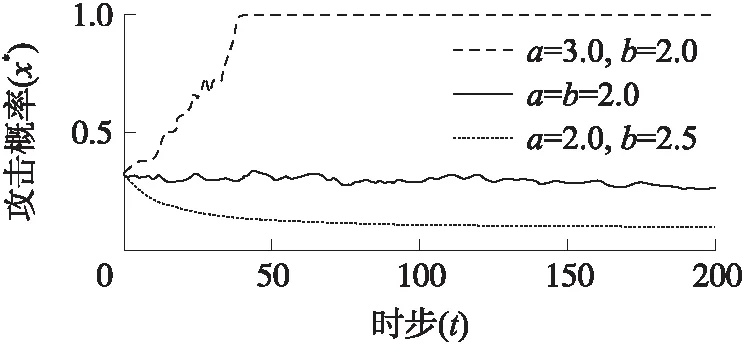
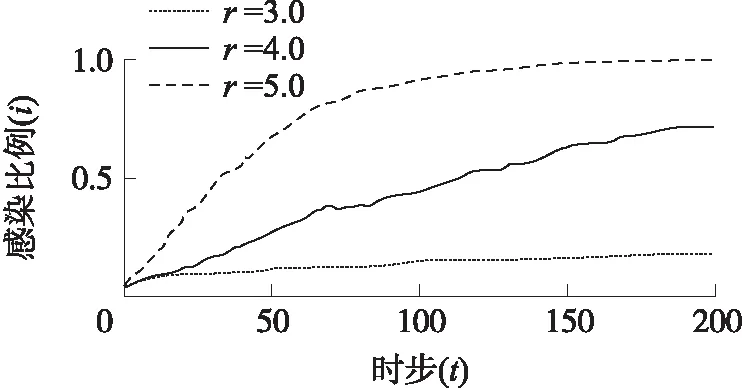
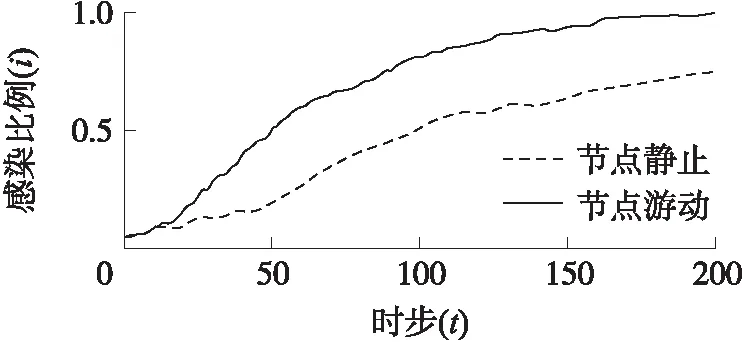
图5 a 图6 恶意节点的攻击策略演化趋势(eD=0.5) 前面的理论传播模型基于一个假设:WSNs中任意两个节点之间可以直接通信。然而,在真实情况中,传感器节点的发射功率一般与通信距离的平方成正比,为了节约能量,每个节点只能与其附近的节点进行通信。由于理论模型无法处理这种情况,本文接下来用元胞自动机方法对WSNs中的恶意程序传播过程进行研究,一方面可以对理论传播模型的结论进行验证,另一方面可以考查通信半径及节点的移动行为对传播速度的影响。 3.3.1 仿真算法 步骤1生成一个如图7所示的规格为100×100的网格,随机选择比例为pw的格子布设传感器节点。 步骤2每个传感器节点与距离自己半径不超过r的节点产生连边(组网),由此生成传感器网络。 步骤3在初始时刻t0=0,随机选取比例为i0的节点设置为恶意节点。 步骤4每个恶意节点在自己的邻居节点(可以与其直接通信的节点)中随机选择一个节点发送信息,其中发送恶意信息的概率为x*,发送正常信息的概率为1-x*。 步骤5若恶意节点选中的节点也是恶意节点,则信息会被直接丢弃。反之,若恶意节点选中的是合法节点,则合法节点会以概率y*对收到的信息进行检测,以概率1-y*不对信息进行检测。当合法节点接收的是恶意程序信息且正好没有启动检测时则会被感染,感染后的节点就变成恶意节点,并能继续向其他节点传播恶意程序;当恶意节点向合法节点发送恶意程序,而合法节点又正好对其进行检测时,恶意节点就会被识别,被识别的恶意节点会被修复,从而又转化为合法节点。 步骤6若t小于预设的模拟步数,则t的值增加1,并转入步骤4继续执行,否则,结束运行。 图7 无线传感器节点分布图(灰色为正常节点, 黑色为恶意节点,pw=0.1,i0=0.05) 3.3.2 仿真结果 设定参数pw=0.1,执行上述模拟步骤,考查不同博弈参数下WSNs恶意程序的传播过程,模拟结果如图8~图13所示。 图8~图10分别对应的是a>b、a=b及a 图8 a>b时感染节点比例演化趋势 (a=3.0,b=2.0,r=5.0) 图9 a=b时感染节点比例演化趋势 (a=2.0,b=2.0,r=5.0) 图10 a 图11 恶意节点的攻击策略演化趋势 (eD=0.5,r=5.0) 由于WSNs中恶意程序的传播过程与通信半径有关,因此,我们进一步研究了传感器节点的通信半径对恶意程序传播速度的影响,在模拟过程中通过修改通信半径的值,得到了不同通信半径下恶意程序的传播曲线,从图12可以看出,在其他参数固定的情况下,恶意程序的传播速度随着通信半径的增加而增大。 在某些实际情况中,有些WSNs中的节点能够不断移动,这会导致网络结构不断变化,基于此,我们进一步对节点移动场景下的恶意传播过程进行仿真,仿真时只需在步骤5结束之后让每个节点随机选择一个方向移动一格,仿真结果如图13所示。从图中可以看出,节点移动时恶意程序的传播速度要高于静态网络。 图12 通信半径对恶意程序传播速度的影响 (eD=2.0,a=3.0,b=2.0) 图13 节点游动对恶意程序传播速度的影响 (a=3.0,b=2.0,r=4.0,eD=0.5) 尽管本文的理论模型和元胞自动机仿真所得的研究结论整体上是一致的,但两者之间仍然存在一些差异,例如:在a>b时,理论模型中恶意程序的传播速度要大于元胞自动机仿真的传播速度,这一点可以分别从图3与图8的比较中反映出来。导致这种差异的主要原因如下:①理论模型假设网络中任意两个节点都可以直接通信,而在元胞自动机模型中,每个节点只能与距离它不超过r的节点通信,传播范围的限制降低了恶意程序的传播速度。②在元胞自动机模型中,由于恶意节点只能攻击其附近的节点,随着时间的推移,就会导致大量恶意节点聚集成簇,这种聚集效应使得大量恶意节点无法有效选择合法节点进行攻击,从而降低了恶意程序的传播效率。值得一提的是,当网络中的节点能够随机移动时能降低成簇效应,从而可以提高恶意程序的传播速度,图13对节点移动和静止时的传播速度进行了比较,比较结果证实这一点。 基于本文的研究结果,可以制定相关的措施来减缓和抑制WSNs中恶意程序的传播,具体措施可以如下:①加大对合法节点感染恶意程序的惩罚(增大b的值),使得b>a,促使其积极应对恶意节点的攻击,提高检测命中率。②当无法改变a>b的关系时,可以通过优化入侵检测算法来降低合法节点的检测能耗(减小eD的值),从而降低恶意程序的传播速度。③适当减小传感器节点的通信半径,这一方面可以降低恶意程序的传播速度,另一方面也可以节约传感器节点的能耗,延长其使用寿命。 本文从博弈论的角度对WSNs中的恶意程序传播问题进行了研究,得到了以下结论:①恶意节点的攻击策略是一个动态策略,其值与网络中节点的感染比例有关,会随时间动态变化。②网络中恶意程序的最终传播结果由博弈参数决定,通过设计合适的博弈机制可以抑制WSNs中恶意程序的传播。③恶意程序的传播速度与通信半径及节点的移动行为有关,通信半径的增大及节点的移动都能加快恶意程序的传播速度。 本文建立的恶意程序传播模型暂时只考虑了节点的两种状态,在实际场景中,节点可能还会存在潜伏状态、免疫状态、死亡状态等状态,甚至不同节点的攻击或防御能力会存在差异,这种含多种状态的复杂异质网络中的恶意程序传播问题是我们未来研究的方向。

3.3 恶意程序传播元胞自动机仿真



4 讨论
4.1 博弈均衡策略的分析
4.2 理论结果与仿真结果的差异分析
4.3 研究结果的应用
5 结束语

