铟钇金属间化合物力学性能的第一性原理计算

何亚丽， 王君龙， 刘秀茹， 刘其军， 张林基， 何 竹， 唐 斌

(1. 西南交通大学物理科学与技术学院，材料先进技术教育部重点实验室，成都 610031;2. 西北工业大学材料学院，凝固技术国家重点实验室，西安 710072)

1 引 言

金属间化合物指由两种或多种金属组分构成的具有特定组织结构的化合物. 金属间化合物中存在金属键和共价键，共价键使得原子间的结合力增强，化学键趋于稳定，从而使其具有高熔点、高硬度的特性；同时由于原子间的结合力增强，扩散减慢，导致蠕变激活能提高，而使得它还具有高的抗蠕变性能. 此外，金属间化合物在氧化性气氛中，表面能生成致密的氧化膜，因而还具有良好的抗氧化性. 金属间化合物诸多的优异特性不仅使之成为科学家们广泛研究的对象，而且作为功能材料表现出了广阔的应用前景[1-5]. 金属铟(In)具有延展性好、熔点低、抗腐蚀、抗磨等优良特性，铟基合金化合物在电子通信、半导体开发、电子工业等多个邻域得到了广泛应用[6, 7]. 例如磷化铟纳米材料因其具有特殊的纳米场效应在光电子邻域有重要应用[6]，铟镓氧化锌作为一种非晶态半导体也广泛地应用在电子工业等邻域[8]. 钇(Y)是典型的稀土元素，对改善和提高材料的光电性质和综合力学性能有很重要的作用[9-15]，其与铟形成稳定的金属间化合物. 近年来，随着计算机的发展，人们利用第一性原理计算对In-Y系统进行了一些研究，研究发现InY、InY2及In3Y这三种In-Y合金分别具有CsCl、Ni2In、Cu3Au结构类型[16-18]. Harris[19]、Havinga[17]等人对In3Y合金的晶格间距、热膨胀性、超导转变温度、室温热电势以及磁化率等性质进行了研究. Yatsenko等人[1]用实验的方法测量出铟基稀土元素的相图，给出相应合金的熔化温度和结构信息，并测出In3Y、InY和InY2三种合金的熔点分别为1110℃、1220℃、1330℃. 然而到目前为止，人们对In-Y金属间化合物的弹性性质等研究相对较少，本文基于第一性原理计算研究了三种In-Y金属间化合物InY2、InY、In3Y的结构稳定性、弹性性能和热力学性质. 通过在密度泛函理论(DFT)框架中使用第一性原理计算，对InY2、InY、In3Y三种In-Y金属间化合物的晶体结构、弹性、热力学性质进行了计算. 根据弹性常数的计算，使用Voigt-Reuss-Hill (VRH) 平均方案确定了InY2、InY、In3Y三种化合物的体积模量B、杨氏模量E、剪切模量G、泊松比ν和德拜温度HD等各种物理量.

2 计算理论及方法

本文的第一性原理密度泛函理论计算软件采用的是Materials studio中的CASTEP模块[20, 21]. 计算过程采用周期性边界条件, 将多电子体系用平面波函数展开表示, 采用超软赝势(ultrasoft)作为平面波基组[22]. 电子间相互作用采用局域密度近似(LDA)中的CA-PZ[23]和广义梯度近似(GGA)中的Perdew-Burke-Ernzerhof[24]交换关联能函数. 选择两种方法中结果较优的来进行其它性质的计算. 本文中利用Broyden-Fletcher-Goldfarb-Shanno[25]优化方法来找到每种物质的局域最稳定结构，平面截断能取为360 eV，关于布里渊区k点铟选取的是7×7×5，其它物质都选取为8×8×9.

3 结果及讨论

3.1 结构性质

铟(In)的晶体结构为体心四方，属于I4/mmm空间群，其晶格常数为a=b=3.249 Å，c=4.941 Å，如图1(a)所示；三种In-Y合金化合物的结构由Materials Studio软件构建，分别为In3Y (Pm3m)、InY (Pm3m)、InY2(P63/mmc)，如图1(b)、图1(c)和图1(d)所示. 钇(Y)晶体为面心立方结构，属于Fm3m空间群，其晶格常数为a=b=c=4.970 Å，如图1(e)所示. 结构优化的结果(表1)表明电子间相互作用采用GGA中的PBE交换关联能函数能使得计算结果与实验值更加的吻合.

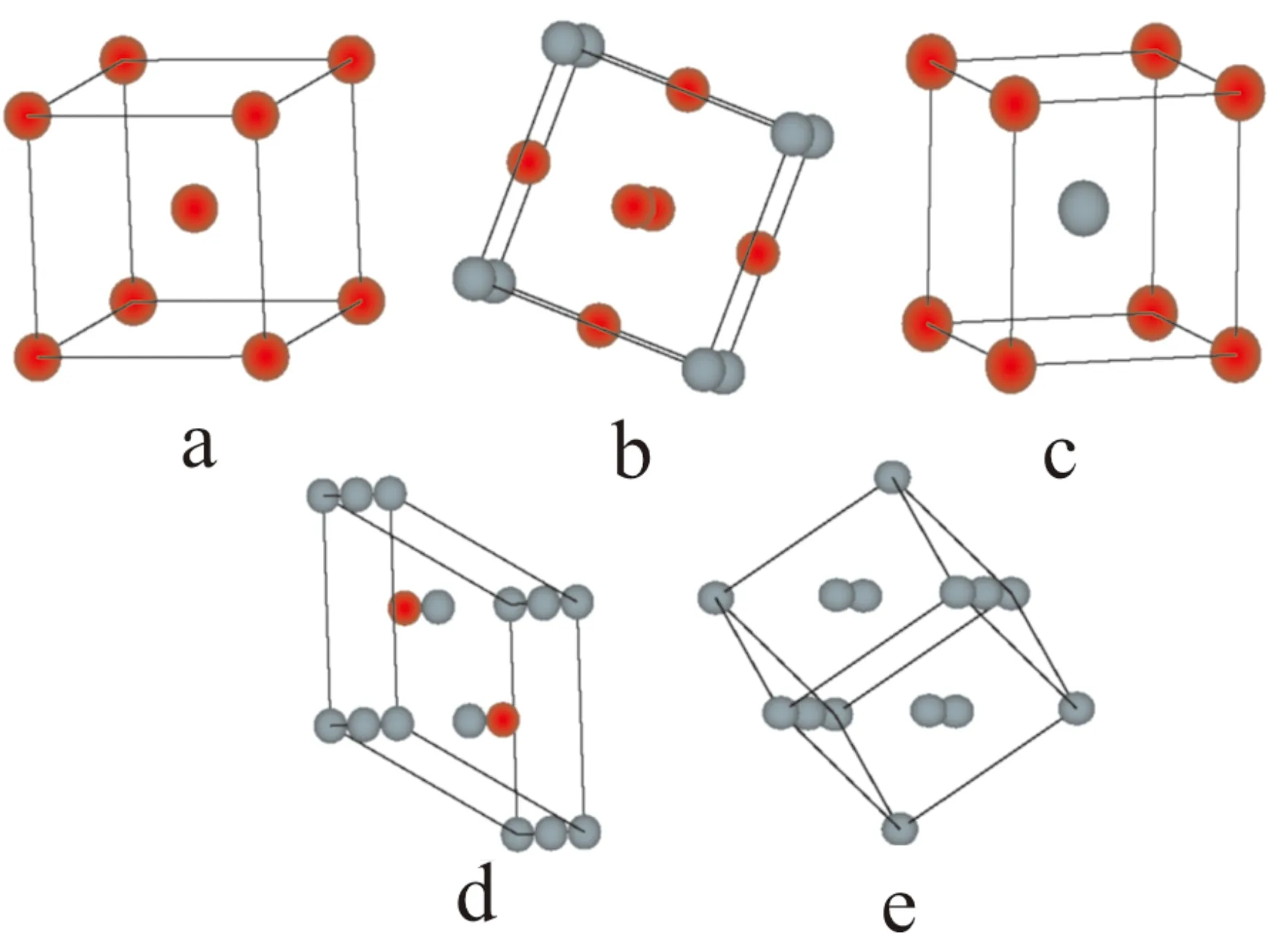
图1 In-Y合金晶体结构:(a) In, (b) In3Y, (c) InY, (d) InY2, (e) Y.Fig. 1 Crystal structures of In-Y alloys:(a) In, (b) In3Y, (c) InY, (d) InY2, (e) Y.

Table 1 Calculated lattice constants together with experimental data

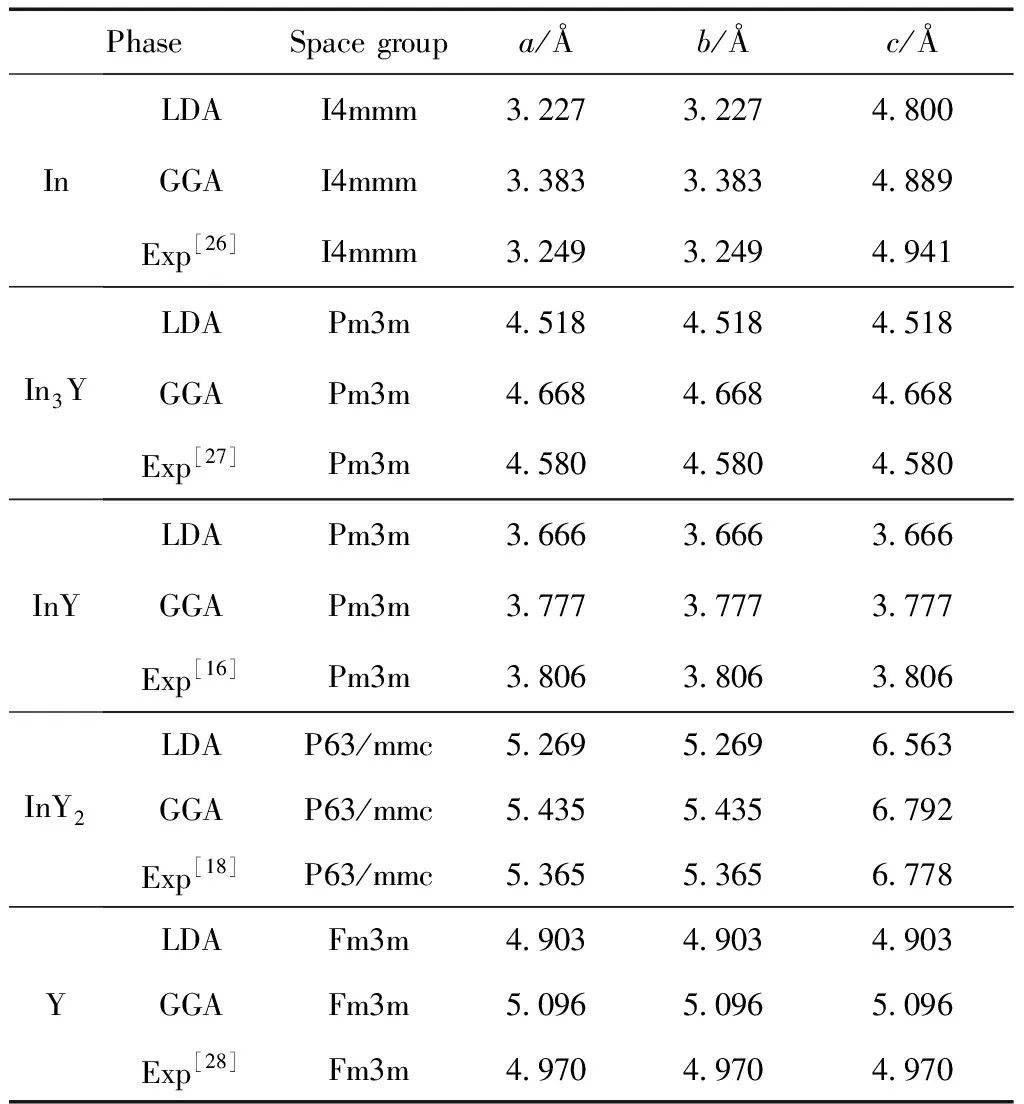
PhaseSpace groupa/Åb/Åc/ÅInLDAI4mmm3.2273.2274.800GGAI4mmm3.3833.3834.889Exp[26]I4mmm3.2493.2494.941In3YLDAPm3m4.5184.5184.518GGAPm3m4.6684.6684.668Exp[27]Pm3m4.5804.5804.580InYLDAPm3m3.6663.6663.666GGAPm3m3.7773.7773.777Exp[16]Pm3m3.8063.8063.806InY2LDAP63/mmc5.2695.2696.563GGAP63/mmc5.4355.4356.792Exp[18]P63/mmc5.3655.3656.778YLDAFm3m4.9034.9034.903GGAFm3m5.0965.0965.096Exp[28]Fm3m4.9704.9704.970

3.2 弹性常数

弹性常数反映了晶体中应力与应变之间的关系，用来描述晶体的力学性质. 对于立方晶系、六方晶系以及四方晶系，独立的弹性常数分别有3个、5个以及6个，力学稳定性条件分别满足:[29]

立方相：C11>0,C44>0,C11>|C12|, (C11+2C12)>0.

(1)

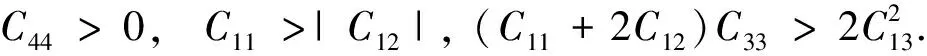
(2)

四方相：C11>0,C33>0,C44>0,C66>0, (C11-C12)>0, (C11+C33-2C13)>0, [2(C11+C12)+C33+4C13]>0.

(3)

由公式(1)～(3)及表2的计算结果可知，两种金属单质In和Y及三种合金化合物In3Y、InY和InY2是符合弹性稳定性条件的. 晶体的弹性常数C11、C22和C33分别体现沿a-轴、b-轴和c-轴抵抗外力的变形能力，由表2可知InY2合金C11的值要明显比其他两种合金的值大，说明InY2相比较其他两种合金在沿a-轴方向上不易被压缩.

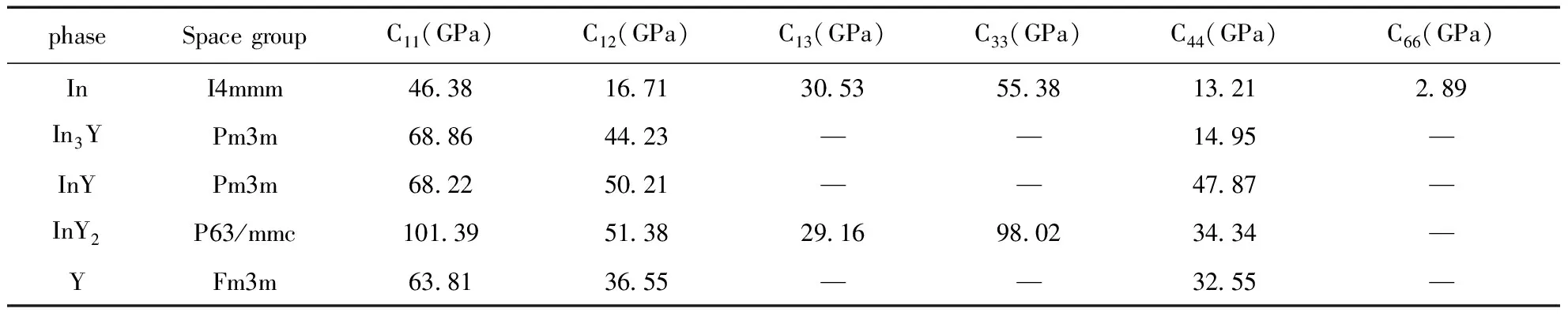
表2 In-Y合金弹性常数计算结果

除了InY2, 其它两种合金是立方结构，因此沿三个方向上的抗形变能力是一样的.

3.3 弹性性质

根据弹性常数及公式(4)～(16)可以计算出三种In-Y合金材料的体积模量B、剪切模量G、杨氏模量E以及泊松比ν，计算结果见表3. 利用Voigt近似[30]和Reuss近似[31]，分别得到体积模量BV、BR，剪切模量GV、GR，通过对两者的数学平均(Hill近似)可以得到理论上最佳的多晶弹性模量，即体积模量BH、剪切模量GH；同时，依据Hill平均值可以求得杨氏模量E以及泊松比ν[32]. 计算公式如下：

立方相：BV=BR=(C11+2C12)/3,

(4)

GV=(C11-C12+3C44)/5,

(5)

GR=5(C11-C12)C44/[4C44+3(C11-C12)].

(6)

六方相：BV=(1/9)[2(C11+C12)+4C13+C33],

(7)

BR=C2/M,

(8)

GV=(1/30)(M+12C44+12C66),

(9)

GR=(5/2)[C2C44C66]/[3BVC44C66+C2(C44+C66)],

(10)

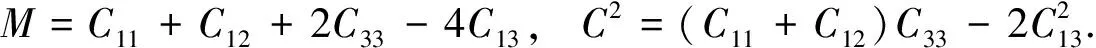
四方相：BV=(1/9)[2(C11+C12)+C33+4C13],

(11)

GV=(1/30)(M+3C11-3C12+12C44+6C66),

(12)

BR=C2/M,

(13)

GR=15{(18BV/C2)+[6/(C11-C12)]+(6/C44)+(3/C66)}-1,

(14)

E=9BG(3B+G)

(15)

ν=(3B-2G)/[2(3B+G)]

(16)

体积弹性模量B表示材料体积抵抗弹性变形的能力, 剪切模量G可以表征材料剪切变形能力的大小, 杨氏模量E描述材料抵抗变形的能力[33]. 由图2易知In-Y三种金属间化合物的B、G和E由大到小的顺序都为InY2>InY>In3Y，表明三种合金中InY2的抵抗体积改变、抗剪切应力的能力以及抗形变能力相比较其它两种合金要强. 这说明稀土金属钇对提高合金材料的抗形变能力是有利的. 同样可以看到，钇单质的B、E及G要比InY和InY2两种合金的值要小，稀土金属中添加铟提高了材料的抗变形能力，但是两种金属的配比对抗形变性能是很关键的，例如当在In3Y合金中其弹性常数就比钇单质的要小，其抗形变能力就比单质时还弱. 从体积模量B可以看出，InY和InY2的值相差不多，说明当In-Y合金中钇的摩尔百分比大于43.63%时体积模量B随稀土金属钇含量的增加变化不大. 从杨氏模量E可知，稀土元素钇含量的增加使得三种合金材料的杨氏模量E依次变大，原则上来说钇含量越多，材料的抗形变性能越强.

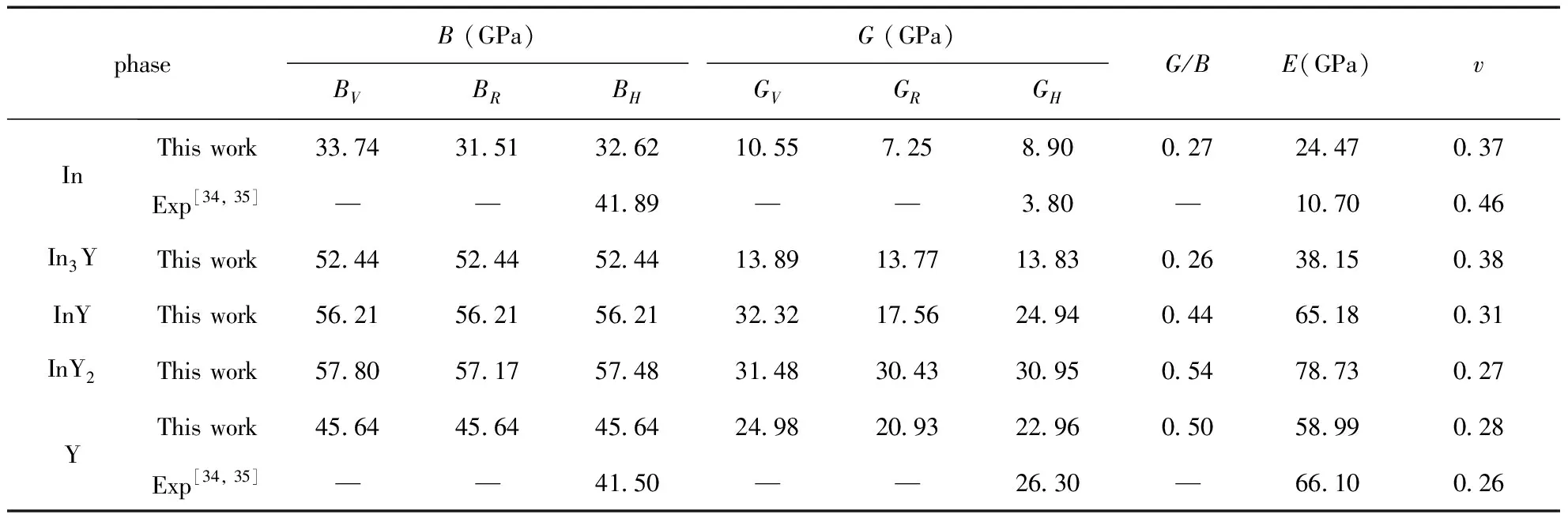
表3 In-Y金属间化合物的弹性模量计算结果

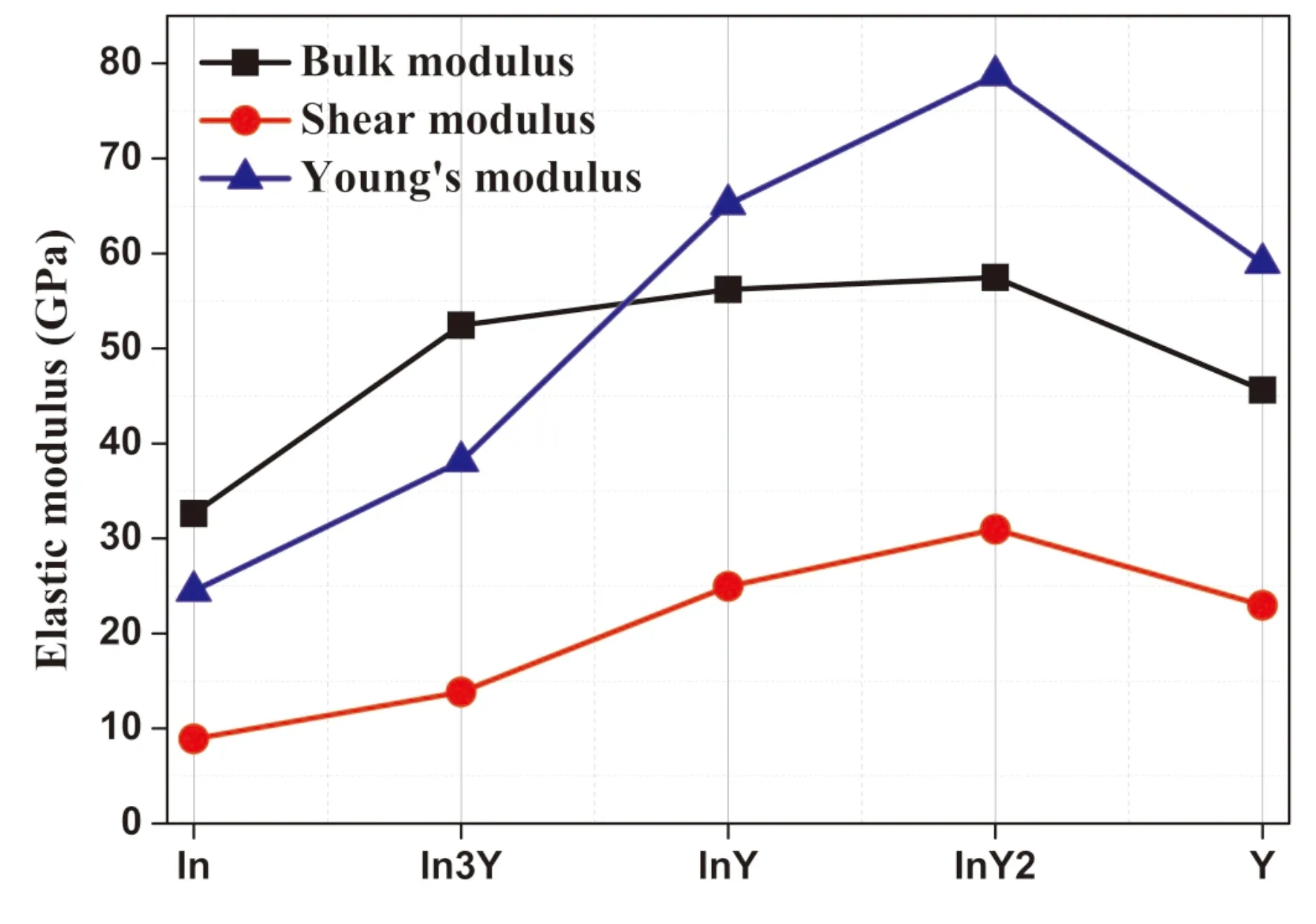
图2 In-Y金属间化合物的体积模量、剪切模量和杨氏模量Fig. 2 Bulk moduli, shear moduli, Young’s moduli of In-Y intermetallic compounds

剪切模量G和体积模量B决定着材料的抗塑性变形和抗断裂能力，它们的比值G/B可以表征物质的延性和脆性，G/B越小，物质的延性越好，通常把0.57作为一个临界点，若G/B>0.57说明材料呈脆性，而G/B<0.57则意味着材料呈延性. 由表3可以得知三种金属化合物全部呈现延性，并且随着钇含量的增加其延展性变弱. 泊松比ν常用来评估材料晶体结构的抗剪切稳定性，ν值越大对应材料结构的塑性越好. 从表3可以看出In3Y化合物的塑性最好，而InY2塑性最差.

弹性各向异性分析对于理解晶体的力学性质具有重要意义，为了评估三种合金的弹性各向异性，本文使用Chung和Buessen等[36]提出的剪切模量(AG)和体积模量(AB)各项异性指数描述，若AB=AG= 0 表示弹性各向同性，AB=AG= 1 则意味着最大程度的弹性各向异性. 公式如下：

AG=(GV-GR)/(GV+GR),

(17)

AB=(BV-BR)/(BV+BR),

(18)

利用Ostioja-Starzewski[37]总结的弹性各向异性因子AU的公式也可以计算化合物的弹性各向异性，若AU=0表示弹性各向同性，AU≠0表示弹性各向异性，并且值越大表示各向异性的程度越大. 公式如下：

AU=5(GV/GR)+(BV/BR)-6.

(19)

根据公式(17)～(19)计算出了各向异性因子，结果见表4. 数据显示InY合金表现较强的各向异性，In3Y合金表现为较强的各向同性，从AB、AG、AU三组值都可以看到相同的规律.

表4 In-Y金属间化合物AB、AG、AU的计算结果

Table 4 Calculation results ofAB,AG,AUof In-Y intermetallic compounds

phaseSpace groupABAGAUInI4mmm0.030.192.35In3YPm3m0.000.010.05InYPm3m0.000.304.20InY2P63mmc0.010.020.18YFm3m0.000.090.97

3.4 热力学性质

德拜温度作为一个基本的物理参量，涉及了物质的很多物理性能，包括比热、弹性劲度常量以及熔化温度等. 德拜温度越高，原子间作用力越大，膨胀系数越小，杨氏模量越大. 德拜温度计算公式如下:[38]

vl=[(B+4/3G)/ρ]1/2,

(20)

vt=(G/ρ)1/2,

(21)

vm=((1/3)((1/vl3)+(1/vt3)))-1/3,

(22)

(23)

其中νl表示纵波声速，νt表示横波声速，νm表示平均声速.ρ为密度，h为普朗克常数，KB为玻尔兹曼常数，n为原胞中的原子数目，NA为阿伏伽德罗常数，M为每个原胞中分子的质量.

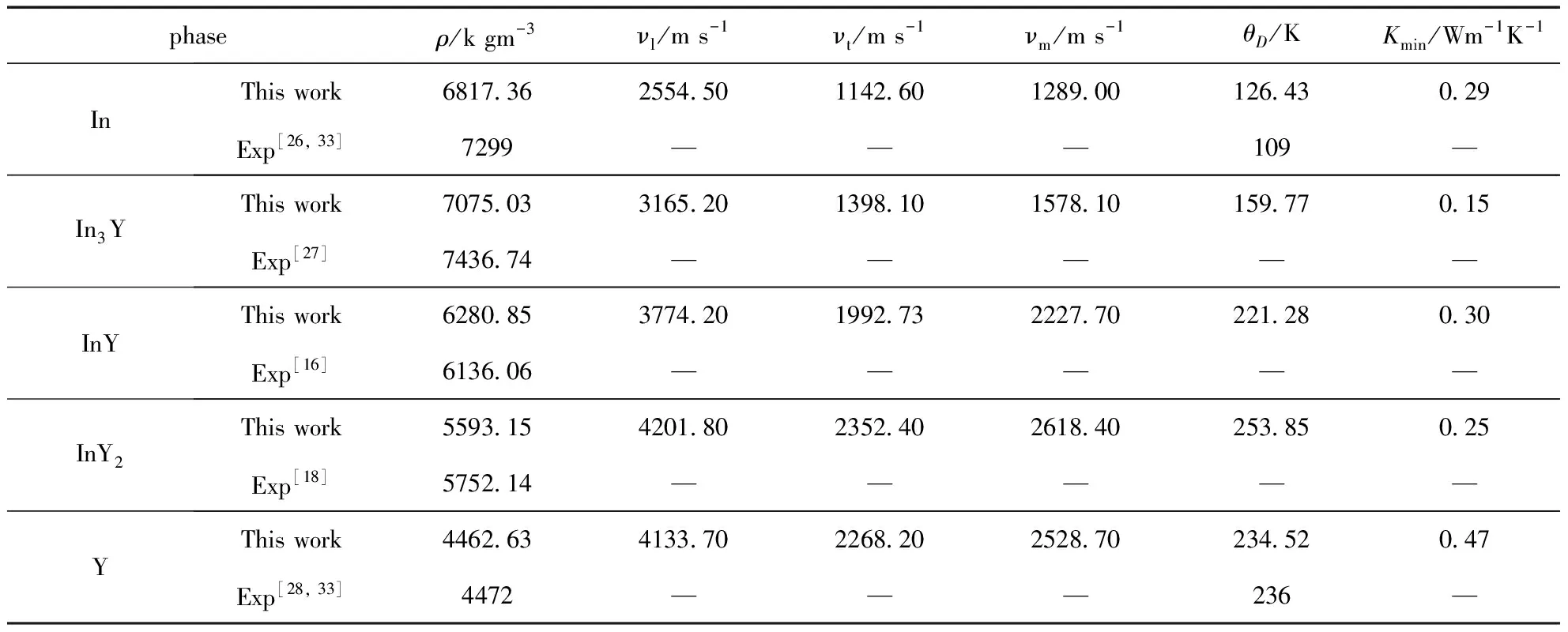
表5 In-Y金属间化合物的νl、νt、νm、θD、Kmin的计算结果

热传导率是材料的本质属性，体现了材料传导热量的能力，在研究材料潜在应用的时候对热传导率进行进一步的分析是非常有意义的. Cahill和Pohl认为最小导热系数可以很容易通过以下公式获得[39]，

(24)

其中n为单位体积原子个数，νt表示横波声速，νl表示纵波声速.

根据公式(20)～(24)计算出德拜温度及热导率，结果见表5. 从德拜温度可以看出，两种单质金属的德拜温度与实验值是比较吻合的. InY2金属化合物的德拜温度相比较其他两种合金要大一些. 这说明InY2合金中的原子间作用力最强. 从热传导率可以看出，InY合金的传导率相比其他两种合金要稍大些. 这些理论预测对以后实验研究提供了一个理论参考.

4 结 论

本文基于密度泛函理论的平面波超软赝势方法，对In-Y金属间化合物的力学结构稳定性、弹性性质和热力学性能进行了较为系统地研究. 通过Materials Studio软件构建了三种In-Y金属间化合物的结构，分别为In3Y (Pm3m)、InY (Pm3m)、InY2(P63/mmc)，结构优化的结果表明电子间相互作用采用GGA中的PBE交换关联能函数能使得计算结果与实验值更加的吻合. 根据计算出的弹性常数及力学稳定性判断准则，得出In3Y、InY、InY2金属间化合物结构在零压零开条件下是稳定存在的，三种合金材料的体积模量B、剪切模量G、杨氏模量E由大到小的顺序为InY2>InY>In3Y，Y单质的B、E及G要比InY和InY2两种合金的值要小，这说明稀土金属钇和铟对提高材料的抗变形能力是有利的，但是两种金属的配比对抗形变性能是很关键的. 通过比较G/B和泊松比ν的计算结果发现三种金属化合物全部呈现延性并且随着Y含量的增加其延展性变弱，In3Y化合物的塑性最好，InY2塑性最差.AB、AG、AU三组数据显示了InY合金表现较强的各向异性，In3Y合金表现为较强的各向同性. 最后还预测了In-Y合金材料的热力学性质，如德拜温度和热导率，InY2金属化合物的德拜温度相比较其它两种合金要大一些，InY合金的热传导率相比其它两种合金要稍大些，说明InY2合金中的原子间作用力最强而InY合金传导热量的能力最强. 这些计算和预测为In-Y合金材料的实际应用和材料设计提供了参考.