交叉型纳米结构下气体位置对阿秒脉冲的影响

刘 航, 冯立强, 2, 3

(1. 辽宁工业大学 化学与环境工程学院， 锦州 121001； 2. 辽宁工业大学 理学院， 锦州 121001；3. 中国科学院大连化学物理研究所分子反应动力学国家重点实验室， 大连 116023)

1 引 言

强激光驱动原子、分子辐射高次谐波(high-order harmonic generation, HHG)作为强场物理以及非线性光学的重要现象被广泛研究近30年. 尤其在获得超短远紫外和软X射线阿秒脉冲的应用上更是获得了极大的关注[1-4].

目前，利用Corkum提出的半经典三步模型[5]，即，‘电离-加速-回碰’，可以有效的解释高次谐波的辐射过程. 基于三步模型可知，谐波辐射过程通常在半个光学周期发生一次，并且其最大截止能量为Ecutoff=Ip+3.17Up，其中Ip为电离能，Up为电子的有质动力势. 因此，对于某一特定的谐波辐射能量有长短两条量子路径共同作用产生[6]，这样在输出阿秒脉冲时会在一个周期出现两个阿秒脉冲序列. 但在实际中，孤立阿秒脉冲更具有应用价值. 因此，如何选取单一的谐波辐射路径来获得孤立阿秒脉冲得到了人们广泛的关注. 目前，对于谐波路径的调控主要分为2大部分，即，(1)少周期激光场或多色组合场方案. 例如：Goulielmakis等[7]利用3.3 fs的单周期激光场驱动惰性气体获得一个80 as脉冲. Feng等[8, 9]利用双色以及三色组合场驱动惰性气体分别获得40 as和sub-10 as的脉冲. (2) 多周期极化门方案(polarization gating, PG). 例如：Sansone等[10]获得了一个130 as的脉冲. Zhao等[11]利用双色极化门方案获得了目前为止实验上最短的67 as的脉冲.

最近10年，一门新兴的技术阿秒-纳米(atto-nanophysics)科学在超快动力学领域得到了广泛关注. 例如：Kim等[12]把惰性气体和激光场输入到金属纳米结构下，实验上获得了一个波长在47 nm的脉冲. 该方案的提出使研究人员可以利用较弱激光场来获得阿秒脉冲，这对阿秒科学的发展非常有利. 随后，Yavuz等[13]研究了金属纳米结构下原子空间位置对谐波辐射的影响. Cao等[14]利用双色场非均匀场方案获得了脉宽在10 as以下的超短脉冲.

虽然，阿秒-纳米科学在超快动力学领域已经被广泛研究，但是纳米结构的排列多是线性排列并且平行于激光偏振方向. 最近，我们提出了一种在线性蝴蝶型纳米结构下，运用多周期极化门技术辐射高次谐波的方案并获得了一个脉宽在30 as的超短孤立阿秒脉冲[15]. 但是在上述方案中，极化门激光场在x，y方向都有贡献，而纳米结构只排列在驱动场方向(x方向). 因此，为了保证x，y方向激光场分量具有类似的增强规律，只能选取对激光增强较小的纳米结构. 为了克服这一缺陷，本文提出了一种在交叉型纳米结构下运用非均匀极化门方案获得孤立阿秒脉冲的方法. 在改方案下用于产生阿秒脉冲的高阶谐波只发生在纳米结构的一侧. 并且，通过叠加平台区的谐波，可获得一个持续时间在33 as的孤立阿秒脉冲. 若无特殊说明，本文采用原子单位[atomic units (a.u.)].

2 计算方法

He原子与激光场相互作用的二维含时薛定谔方程为[16, 17],

xEx(x,t)+yEy(y,t)]φ(x,y,t)，

(1)

(2)

Edriven(x,t)=(1+g(z))[E1f(t+

tdelay/2.0)cos(ω1t)+E2f(t-tdelay/2.0)cos(ω2t)]，

(3)

Egating(y,t)=(1+g(z))[E1f(t+

tdelay/2.0)sin(ω1t)-E1f(t-tdelay/2.0)sin(ω1t)]，

(4)

f(t)=exp[-4ln(2)t2/τi2],i=1,2，

(5)

其中，Ei，ωi，τi(i= 1, 2)为激光场振幅，频率和半高全宽.tdelay为2束激光场延迟时间.g(z=x,y) =βz表示空间非均匀场形式. 这里我们采用一阶近似并取β= 0.005[18].x0，y0为He原子空间位置. 其中，x0，y0< 0或x0，y0> 0分别表示He原子位置偏离纳米结构中心负向或正向.

高次谐波表示为：

(6)

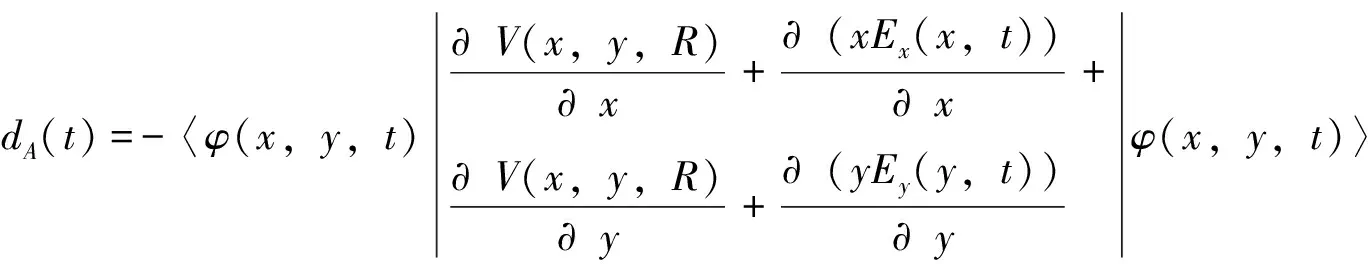
阿秒脉冲的瞬时强度可表示为：

(7)

3 结果与分析

图1(a)给出了本文采用的交叉型纳米结构的空间排列示意图以及He原子的注入位置. 图1(b)给出了交叉纳米结构下He原子在单色场(tdelay= 0 fs)和PG场(tdelay= 8 fs)分别驱动下谐波辐射特点. 本文采用的左右旋转圆偏振激光场为20 fs-1600 nm，I= 7.0×1013W/cm2. 由图可知，在单色场情况(x0=y0= 0 a.u.)，谐波截止在310ω1附近. 随着极化门效应的引入(PG，x0=y0= 0 a.u.)，谐波截止能量有所减小，但是谐波光谱干涉结构也明显减小，这有利于获得孤立阿秒脉冲. 当He原子远离纳米结构中心点时(例如：x0=y0= ± 70 a.u.)，谐波截止能量可以进一步延伸到380ω1附近. 具体来说，当x0=y0= -70 a.u.时，不仅谐波截止能量得到延伸，而且谐波辐射强度较x0=y0= 0 a.u.的情况有1个数量级的提高，进而可以获得一个116 eV的连续平台区，这显然非常有利于获得高强度阿秒脉冲. 当x0=y0= 70 a.u.时，虽然谐波截止能量也有延伸，但是谐波辐射强度没有明显特高，并且其谐波辐射干涉结构较大，这并不利于获得高强度的孤立阿秒脉冲.

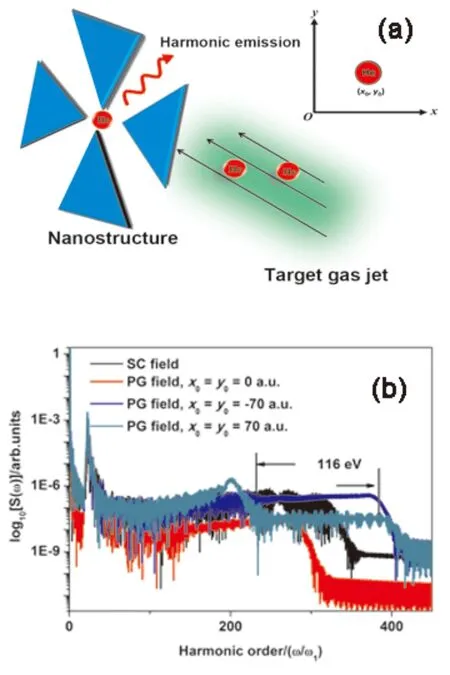
图1 (a) 交叉型纳米结构的空间排列示意图. (b) 交叉纳米结构下He原子在单色场和PG场分别驱动下谐波辐射特点. Fig. 1 (a) The schematic of the crossed nanostructure. (b) Harmonic spectra from He atom driven by the single-color and the PG inhomogeneous fields in the crossed nanostructure.

为了理解纳米结构下空间非均匀场驱动气体辐射谐波的过程，图2和图3给出了上述激光场的时空分布以及He原子在上述条件下谐波辐射的时频分析图[19]. 首先对于单色场情况，由三步模型理论分析图2(a)可知，电子电离发生在激光瞬时振幅附近(标记为i1～5)，随后自由电子在激光场作用下加速，当激光反向时加速电子有几率返回母核并发生回碰辐射高次谐波(标记为r1～5). 因此在谐波辐射过程中会呈现5个主要的辐射能量峰，即，图3(a)所示 的P1～5. 这是导致谐波辐射干涉结构明显的原因. 对于PG场，x0=y0= 0 a.u.情况，由于驱动场场强减弱[见图2(a)]，导致电子电离几率减小，因此谐波辐射能量峰的截止能量也被减小，如图3(b)所示. 并且，由于极化效应，辐射峰P1和P5的强度都被明显减弱，因此导致谐波强度下降以及谐波干涉结构的减小. 但是，当谐波能量高于180ω1时，谐波光谱贡献依然来自于P2～4能量峰，因此依然不利于孤立阿秒脉冲的产生. 对于PG场，x0=y0= ±70 a.u.的情况，由于气体空间位置的变化激光驱动气体时呈反对称增强特点. 例如：当x0=y0= -70 a.u.时，驱动场沿负方向增强幅度要大于正方向；当x0=y0= 70 a.u.时，驱动场沿正方向增强幅度要大于负方向，如图2(b)所示. 因此，对于x0=y0= -70 a.u.的情况，电离电子在负x方向加速获得的能量要远大于在正x方向加速获得的能量，因此导致谐波辐射能量峰P3得到明显延伸，如图3(c)所示. 并且，当谐波能量大于230ω1时，谐波光谱只由P3贡献，而且其长量子路径对谐波辐射能量峰的贡献被明显压制. 这是导致谐波光谱呈现平滑连续平台区的原因. 对于x0=y0= 70 a.u.的情况，电离电子在正x方向加速获得的能量要远大于在负x方向加速获得的能量，因此导致谐波辐射能量峰P2和P4得到明显延伸，如图3(d)所示. 但是，当谐波能量大于230ω1时，谐波光谱由2个谐波辐射能量峰贡献产生(P2和P4)，并且其强度要小于P3. 这是导致其谐波光谱强度较低并且呈现较大的干涉结构的原因.

图2 (a)单色场以及极化门场的激光包络图. (b) 极化门驱动场的时空分布. Fig. 2 (a) Laser profiles of the single-color (SC) field andthe PG field. (b) The laser profile of the driven field in time and space.

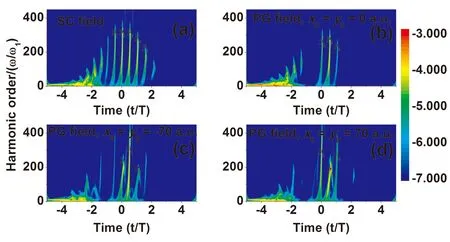
图3 谐波辐射时频分析图(a)单色场；(b) PG场，x0 = y0 = 0 a.u.；(c) PG场，x0 = y0 = -70 a.u.；(d) PG场，x0 = y0 = 70 a.u.. Fig. 3 The time-frequency analyses of the harmonics for the cases of (a) single-color field; (b) PG field with x0 = y0 = 0 a.u.; (c) PG field with x0 = y0 = -70 a.u.; (d) PG field with x0 = y0 = 70 a.u..

通过上述分析可知，当气体沿纳米结构负方向注入时，用于产生阿秒脉冲的高阶谐波只发生在纳米结构的一侧，这显然非常有利于孤立阿秒脉冲的输出. 因此，最后通过直接叠加该情况下(PG场，x0=y0= -70 a.u.)谐波光谱的230ω1到380ω1次谐波，可以获得一个脉宽在33 as的超短孤立阿秒脉冲，如图4所示.

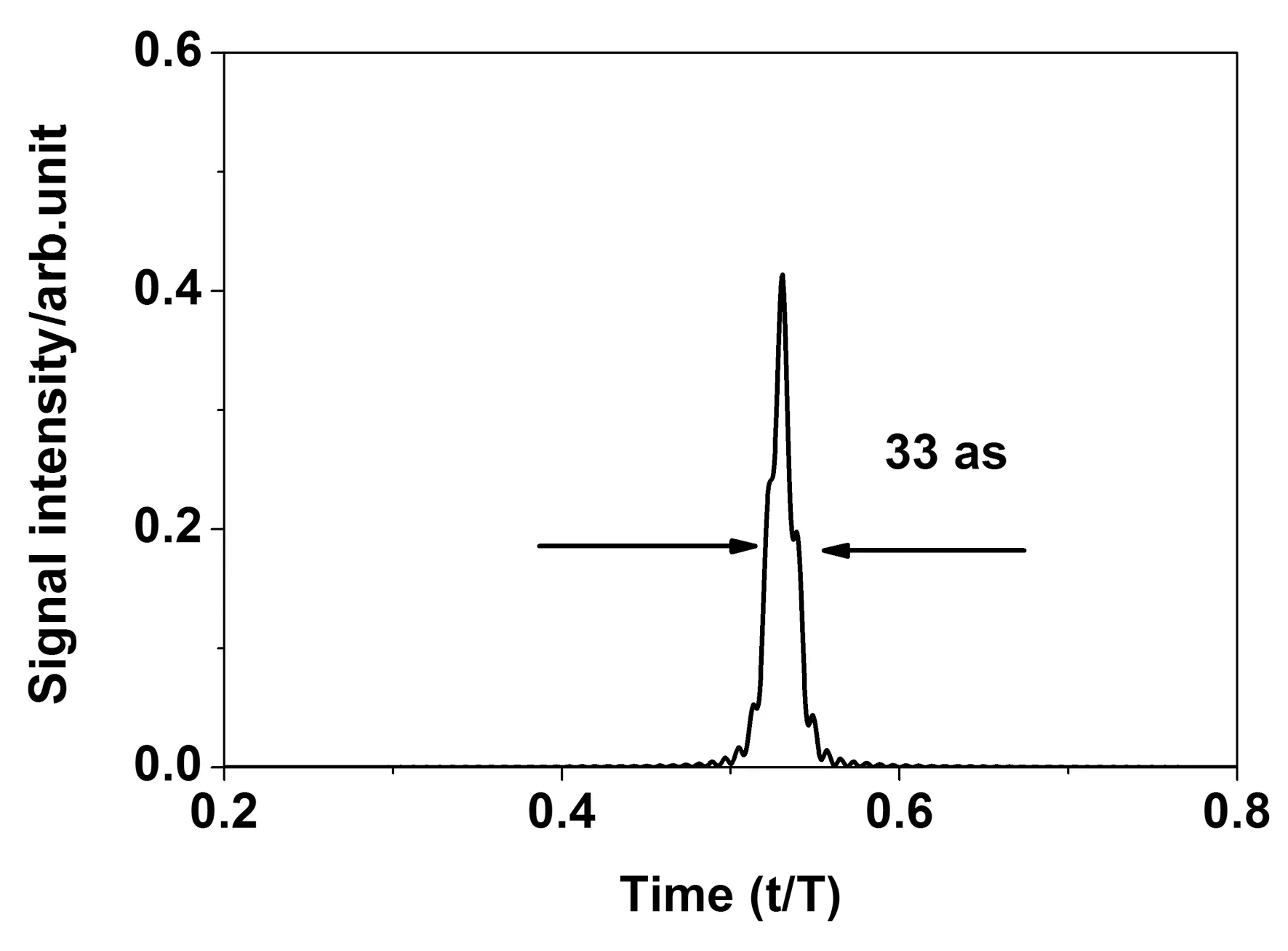
图4 阿秒脉冲波形图. Fig. 4 The temporal profiles of the attosecond pulse.

4 结 论

综上所述, 本文提出了一种在交叉型纳米结构下运用非均匀极化门方案获得孤立阿秒脉冲的方法. 在改方案下用于产生阿秒脉冲的高阶谐波只发生在纳米结构的一侧. 并且，通过叠加平台区的谐波，可获得一个持续时间在33 as的孤立阿秒脉冲. 由于在本方案中采用了交叉型纳米结构的设计，因此保证x，y方向激光场分量具有相同的增强规律，这样就克服了之前选用线性纳米结构方案是只能选取对激光增强较小的纳米结构的束缚.