基于功率预测误差修正的日前风电出力分布估计
吴晓刚,鲁宗相,乔颖
(1.云南电力调度控制中心,昆明 650011;2.清华大学,北京 海淀 100084)
0 前言
目前风电场装备的功率预测系统大多提供的是点功率预测信息。然而,由于数值天气预报等技术的限制,风电功率预测结果的准确性并不是很高,如果只有风电场的点功率预测值,那么风电出力的预测结果就会呈现出很大的不确定性,影响风力发电的运行与控制[1]。相比于点功率预测而言,区间预测能够提供更加丰富和有用的信息,更能适应风电并网运行分析和调度控制的需要[2-3]。
关于风电出力分布的估计方法,国内外已经取得了许多研究成果。文献[4]基于t locationscale分布,提出了一种风电功率的区间预测方法,该方法使用t location-scale函数拟合风电预测误差的概率分布曲线。该方法适用于精确获取风电场预测误差的概率分布函数。文献[5]在有限的历史运行数据基础之上,基于蒙特卡罗方法建立了风电场的风速-风电功率模型,并利用随机优化方法对含有风电并网的电力系统运行方式做了优化。文献[6]采用风电功率预测误差的方均根值std作为修正因子,在原始点功率预测结果的基础之上,通过加减std来得到风电场预测出力的上下限,该方法在风电预测误差较大的情况下容易使包络曲线变宽。文献[7,8]证明了柯西分布和双曲线分布对风电预测误差的拟合效果要明显优于正态分布,但是柯西分布和双曲线分布的参数拟合较为复杂,而且对风电预测误差“尖峰厚尾”的分布特点拟合得不够准确。
另一方面,由于影响风机实际出力的因素有很多,使用不同模型描述风电场预测误差分布的效果会有所不同。所以,研究影响风电功率预测误差的因素对提高风电功率预测精度具有十分重要的意义,国内外在这方面也取得了许多研究成果。
文献[9]通过寻找与待测日前一天预测结果相似的历史数据,分析相似日的预测误差特点来拟合待测日功率预测的误差分布,这种方法需要大量的数据统计,计算过程比较繁琐。文献[10]认为风电预测的误差与功率的变化速率和预测风速的误差水平有关,需要对预测的风速误差进行统计分析,并计算对应时段内功率曲线的斜率。文献[11-13]提出风电功率预测误差与风电场预测系统采用的预测方法、提前预测的时间和近期风电出力的波动水平等因素有关。文献[2]认为风电功率的预测误差主要受到出力大小、预测功率的波动性等因素的影响,并利用相应的统计量将其量化,然后对这些因素与风电功率预测误差的相关性进行统计分析,得到风功率预测误差的上下限。文献[14]认为风功率预测误差主要与风速等气象因素有关,并在历史实际运行数据的基础之上建立了风电功率超短期预测的条件概率模型,用以分析预测结果的不确定性。
但是,受限于数值天气预报(NWP)技术提升难度大的障碍,风电功率预测结果短时间内在精度上很难有较大的提高,所以有必要结合工程实际情况,综合考虑影响风电预测误差的重要因素,对风电功率的区间预测方法进行研究。本文基于实际运行数据,对影响风电场日前功率预测误差的因素展开了深入的研究,并在前人研究成果的基础之上对风电场日前风电出力分布的估计方法做了优化。
1 研究的整体思路
风电预测误差描述的是一段时间内风电预测功率与实测功率之间的偏差。假设误差统计是稳定的,那么我们就可以使用历史数据的预测误差来分析并估计未来时刻预测误差的分布情况[3-4]。
为此,首先要对风电历史运行数据中的预测风速、预测功率和实测功率进行预处理,然后对其进行统计分析,研究影响风电功率预测误差的作用因子,找出他们之间的对应关系,并修正风电预测功率,最后在修正功率的基础之上估计出风电出力的上下限。具体过程如图1所示。
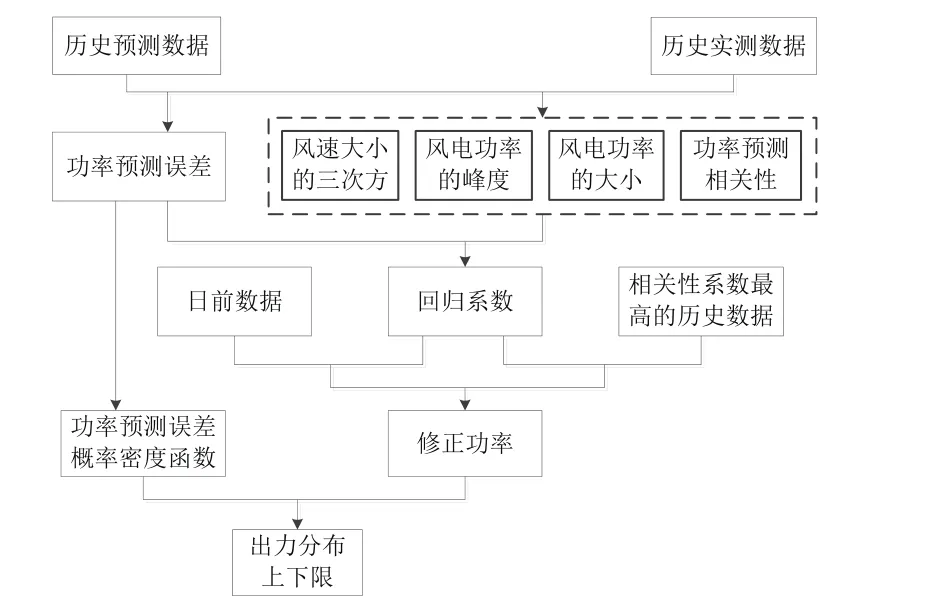
图1 功率修正和预测分布估计流程图
2 影响风电预测误差的因素分析
本节采用具体风电场的实际运行数据,对风速大小的三次方、风电功率的峰度、风电功率的大小,以及预测功率相关性这四个量与风电功率预测误差之间的相关性进行了统计分析。采用的是中国北方某风电场2016年的运行数据,并以风电功率的实测值和预测值之差E作为风电功率的预测误差,如式所示。
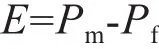
式中:Pm是风电功率的实测值,Pf是风电功率的预测值。
为了描述各个影响因子与预测误差之间的相关性,采用皮尔逊相关系数来描述这种相似关系,用r表示,计算公式为:

式中:n为样本量,Pf,i,Pm,i和分别为两个变量的观测值和均值。
2.1 异常数据识别与处理
在进行预测误差分析之前,首先要对风电场历史运行数据中的预测风速、预测功率和实测功率进行预处理。
异常数据的识别与处理是分析影响风电功率预测误差因素,以及开展后续研究工作的重要环节,本文根据工程实际情况将异常数据划分为以下三种类型:
1)通讯故障产生的异常数据:这类异常数据的特征是,当实际风速大于切入风速的时候,风电功率数据的变化幅度较小,且维持在零附近。
2)弃风限电产生的异常数据:这类异常数据的特征是,当风速变化时,风电功率数据的变化幅度较小,且维持在风电机组(风电场)功率特性曲线上限之外的一定范围内。
3)机组脱网产生的异常数据:这类异常数据的特征是,当风速变化时,风电功率数据的变化幅度较小,且维持在风电机组(风电场)功率特性曲线下限之外的一定范围内。
以上所提的三种异常数据的示意图如图2所示。

图2 典型异常数据点
为了更加高效地分析风电预测误差特性,本文采用文献[15-16]中提出的基于四分位算法的数学模型对这些异常数据进行识别,并根据其特点进行校正和重构。
2.2 风速大小的三次方对预测误差的影响分析
风电机组的出力水平主要由风速大小决定。基于数值天气预报方法进行功率预测的风电场,通常是在风电场的功率特性曲线基础之上进行的,输入量为风速大小,输出量为风电功率预测值。经典的风电场功率特性曲线描述的是风电功率与风速之间的关系,是一个三次多项式,如式所示。

为了充分利用风电场的出力特性与风速之间的关系,本文选择风速大小的三次方作为影响风电功率预测误差水平的一个因子,如式所示。

图3给出了风电预测误差与风速大小三次方之间的关系曲线,二者之间的相关系数r=0.4587,说明风速大小的三次方与风电预测误差之间具有比较强的相关性。

图3 风速大小三次方与预测误差的相关性统计图
2.3 风电功率的峰度对预测误差的影响分析
峰度,即峰态系数,被用来衡量概率密度曲线在平均值处峰值的高低程度,能够形象地反映曲线尾部的厚度,用k表示,其计算公式如式所示。
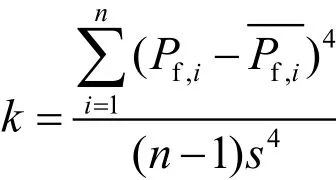
式中:Pf,i是样本测定值,是样本n次测定值的平均值,s为样本的标准差。
峰度反映了数据在中心点处的聚集程度,这可以用来衡量风电功率预测出力的波动程度。在短时间内(如1小时),如果峰度较大的话说明风功率波动比较大,这会给预测增加难度。
图4给出了风电预测功率的峰度与预测误差之间的关系曲线,二者之间的相关系数r=0.3961,说明两者之间具有一定的正相关关系。

图4 风电功率峰度与预测误差的相关性统计图
2.4 风电功率的大小对预测误差的影响分析
风电预测误差与风电功率的大小有关。如果风电功率很大的话任何影响因子的微小变化都会引起预测结果的较大波动[10],这给功率预测的准确性带来了很大的挑战。所以本文选择风电功率的大小作为影响预测误差的一个因子,并采用预测功率的算术平均值来表示这一个量,计算公式如式所示。

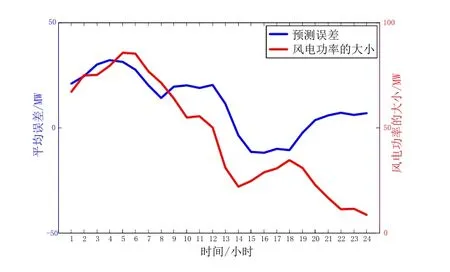
图5 风电功率大小与预测误差的相关性统计图
图5给出了预测功率的平均值和预测误差的关系曲线,从图中可以看出二者在很大范围内的变化趋势很接近,其相关性系数r=0.5361,说明二者之间具有很强的相关性。
2.5 功率预测相关性对预测误差的影响分析

图6 功率预测相关性与预测误差的相关性统计图
为了衡量功率预测方法的有效性,本文引入了功率预测相关性β,用来描述一段时间内的预测功率与实测功率之间的相似程度,计算公式如式所示。

式中:σf是一段时间内功率预测值的标准差,σm是相同时间内功率实测值的标准差,rf_m是这段时间内预测值和实测值的相关系数,PN是对应时段风电场的开机总容量。图6给出了预测误差和功率预测相关性之间的关系曲线,二者之间的相关系数r=0.4125,说明他们之间具有一定的正相关性。另外从图6可以看出在某些时段里功率预测相关性和预测误差之间的变化趋势基本一致,说明在这些时间段里二者之间强相关。
3 修正风电功率预测误差
本文采用多元线性回归方法建立预测误差的估计模型。
多元线性回归是根据历史的样本数据建立某个因变量与多个自变量之间的对应关系,从而在已知某段时间内多个自变量的情况下,预测未来时刻该因变量的值[17]。在多元线性回归分析中,记因变量为Y,自变量的集合为X={x1,x2, … ,xp},样本容量为n,第i个样本在第j个变量处的取值为xi,j(i=1, 2, … ,n;j=1, 2, … ,p),根据自变量和因变量的样本数据,定义矩阵:
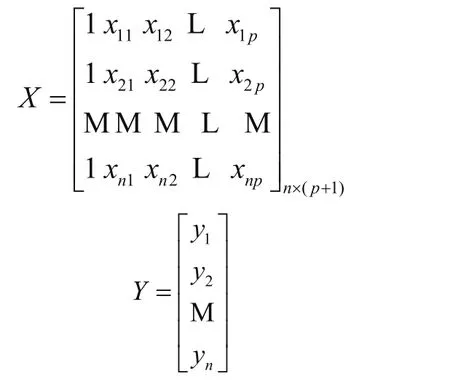
进而定义增广矩阵:

增广矩阵的叉积阵为:

多元线性回归的最小二乘估计量B可以由式计算得到。

由此便可以建立回归方程:

由于相近的时间段里风电出力变化不会太剧烈,所以可以对这些数据按时间段进行划分,按式及式至式分别计算出每个时间段内的预测误差E、风速大小的三次方V、风电功率的峰度k、风电功率的大小和功率预测相关性β,然后令按式计算出B,再根据待测日日前的数据和与待测日预测数据相关性系数最高的历史数据,按式、式至式以及式分别计算出预测功率的误差估计值Ec1和Ec2,最终的风电功率预测误差修正量Ec由式计算得到。

然后按照式便可以求出预测功率的修正值P1f。

4 估计风电预测出力的上下限
为了得到风电场功率预测出力的上下限,本文采用文献[18]中提出的广义误差分布模型来提取风电预测误差的概率密度特征,计算公式如式所示。

式中的每一个参数都可以用极大似然估计法得到。
然后以风电场功率预测误差的平均值为中心计算出各个置信水平下对应的置信区间。按照所要求的预测精度选择适当的置信度,对应的置信区间为(μ-ξ, μ+ξ),根据补偿后的功率预测值,便可以估计得到风电功率的上限值Pf,max和下限值Pf,min:

5 算例分析
本文以中国北方某风电场2016年全年的风电运行数据作为研究对象进行了大量的算例分析,该风电场的装机容量为165 MW,时间间隔为15分钟一个点。
首先对该风电场前11个月的实际运行数据进行异常数据识别与处理,然后分别拟合出式至式中的各个参数,如表1所示,从而得到风电场功率预测误差的概率密度函数。

表1 广义误差分布模型中各参数的估计量
再根据该函数计算出不同置信水平下的置信区间,如表2所示。

表2 不同置信水平下的置信区间
然后选择待测日前一天,以及与待测日预测数据相关性最高的历史日的数据,以1小时为统计时间段,每15分钟更新一次,分别计算出各个时刻风电预测误差的修正量Ec,由此计算出修正后的待测日预测功率P1f,图7给出的是2016年12月1日的风电功率修正情况。

图7 预测功率修正前后的对比图
表3给出了风电预测功率修正前后的统计结果,其中平均绝对值误差MAE和相对误差ε的计算公式如式所示。


表3 功率预测修正前后的统计结果
由图7和表3可以直观地看出修正过后的风电功率在精度上有了明显的提高,尤其是在出力较低的时段,所提的方法能够很好地修正预测功率的误差。另外从图7还可以看到,在功率波动性不大的后半段时间里,修正后的曲线和实测功率曲线基本吻合,说明在这段时间里所提方法的精度很高,通过计算可知在这段时间里的平均绝对值误差MAE=6.7812MW,相对误差ε<0.15的比例为65.43%。
选择85%的置信度,在修正过后的预测功率的基础之上计算出待测日的风电出力上下限。图8是2016年12月1日的风电预测分布估计结果图,统计结果表明,有91.21%的实际出力值都分布在了估计区间内。
从图8可以看出,风电功率的预测误差随着时间的变化而变化,在风电功率幅值和波动性大的时间段里误差估计值偏大,导致区间分布的估计范围也相应地偏大。

图8 风电功率预测分布的估计结果图
6 结束语
本文在经典的风电功率特性曲线基础之上,研究了基于功率预测误差修正的日前风电出力分布的估计方法,得到的主要结论如下:
1)通过对大量的实际运行数据进行统计分析,验证了风电功率的预测误差水平受到风速大小的三次方、风电功率的峰度、风电功率的大小和功率预测相关性等多个因素的影响,然后利用多元线性回归方法建立了功率预测误差与这些影响因子之间的对应关系,并修正原始的点功率预测值。
2)通过引入广义误差分布模型估计风电功率预测的上下限。从整个分布估计过程来看,所提的方法计算成本很低,需要的计算数据容易获取;从分布估计的效果来看,所提方法的计算结果精度很高,既延续了风电功率的历史变化规律,又考虑了日前风电出力的具体情况,这对预测部门和调度部门校核风电功率预测、安排日前发电计划具有一定的参考价值。
总体而言,风电功率的区间预测相比于点功率预测而言更能适应风电并网运行分析和调度控制的需要,在今后有关大规模风电并网的研究当中应该给予更多的关注。

