无限长双曲柱面带电导体的场分布

张拴柱

(长治学院电子信息与物理系，山西 长治 046011)

在一般的电磁学教科书中，讨论无限大的带电导体平板的例题、习题很多，但对带电导体不是平板而是其他“曲面”板的问题很少涉及到。本文采用椭圆柱面坐标系，直接求解拉普拉斯方程，推导出了无限长带电体为理想导体薄片制成的双曲柱面场分布的解析式，画出了等势(面)线和电力线分布、计算出了双曲柱面上电荷密度分布以及由双曲柱面组成电容器的电容，在此基础上还讨论了一些其他特殊情形下的场的分布和电荷的分布。

1 无限长双曲柱面带电导体的场分布

设有用理想导体薄片制成的无限长带电双曲柱面导体，垂直于z轴平面与双曲柱面相截，得的是一条双曲线，它有A、B两条曲线，如图1所示。A导体上电势V1，B导体电势V2，且V1>V2。在xOy平面截得的A、B曲线方程为

(1)

两支分别为：x>0为A支双曲线；x<0为B支双曲线。

图 1

引进椭圆柱面坐标系，它与直角坐标系的关系为

(2)

拉梅系数

(3)

在椭z圆柱面坐标系中，坐标曲面是ξ=常数：为椭圆柱面

(4)

η=常数：为双曲柱面

(5)

z=常数：为平行于xOy面的一族平面

z=C(常数)

(6)

在椭圆柱坐标系中，两“曲面”板之间的电势φ满足拉普拉斯方程

(7)

带电导体为双曲柱面且无限长，由对称性可知这是一个平行平面场问题。又因为带电导体双曲柱面在xOy面上与椭圆柱坐标系中的双曲线重合，在带电导体双曲柱面上，电势φ是与ξ和z无关的常量，因此φ若只是η的函数，就可以满足该问题的边界条件，故取电势φ分布函数只与η有关，与参量ξ、z无关，即

φ=φ(η)

(8)

因此，电势φ的拉普拉斯方程变成了

(9)

解方程得

φ=Aη+B

(10)

其中：A和B是两个积分常数，由边界条件确定。

由边界条件确定A和B两个常数：

V1=Aη1+B

(11)

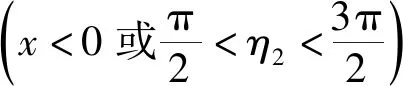
V2=Aη2+B

(12)

联解

(13)

而

(14)

所以

φ=Aη+φ0

(15)

将带电导体A双曲线方程(1)(x>0)，与一族双曲线方程(5)比较可得

同理，将带电导体B双曲线方程(1)(x<0)，与一族双曲线方程(5)比较可得

由此可求得

(20)

所以

(21)

电场强度E的分布。由E=-φ两“曲面”板之间的电场分布

(22)

而

(23)

代入式(22)，得

(24)

当讨论的点是在带电A双曲柱面上，即取η=η1，把式(16)、(17)代入式(24)得

(25)

当讨论的点是在带电B双曲柱面上，即取η=η2，把式(18)、(19)代入式(24)得

(26)

下面求等势面和电力线分布函数。

电势等势面：

当φ=Aη+B=常数时，则一定有η=常数，而η=常数，则为一族双曲柱面组成

(27)

因此等势面是一族双曲柱面，与带电双曲柱面有共同的焦点，在与垂直于z轴的平面相截得到的是一族等势双曲线。

电力线：

由正交曲线坐标系知识可知，电力线应该满足微分方程

(28)

由于Eξ=0，所以dξ=0，则ξ=常数，而ξ=常数，对应是一族椭圆柱面，其方程

(29)

同理，由于Ez=0，所以dz=0，则z=常数，而z=常数，对应的是一族平面

z=C

(30)

式(29)和式(30)联立即是电力线方程，是一族椭圆曲线(一部分)，如图2所示。

图 2

结论：两“曲面”板之间的双曲柱面、椭圆柱面与z=常数相截所得的两族交线：一族双曲线(等势线)，另一族椭圆线(电力线)，它们有共同的焦点。

2 双曲柱面导体上的电荷分布

下面求双曲柱面上的电荷分布，由电磁场边值关系

(31)

而

(32)

所以在带电A双曲柱面上

(33)

由此看出，双曲柱面上的电荷分布不均匀。下面看两个特殊的点：

(1) 双曲线的弧顶点处(a,0)

(34)

(2) 当y2→∞，即开口无限大时，此处看作平面

σmin→0

(35)

3 若有A、B两个双曲柱面导体薄片组成电容器，计算电容

如图1所示，A、B两个双曲柱面组成电容器。首先求出带电A双曲柱面所带电荷QA。

(36)

在椭圆柱面坐标系中，若带电导体双曲柱面A正好是当坐标系中η=η1为常数时的一个坐标曲面，由此可知，存在常数η1使得

(37)

所以沿轴线方向L长双曲柱面的电荷

(38)

由x=cchξcosη得

(39)

所以

(40)

故沿轴方向长为l的双曲柱面电容器的电容

(41)

讨论

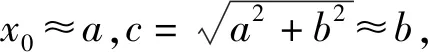
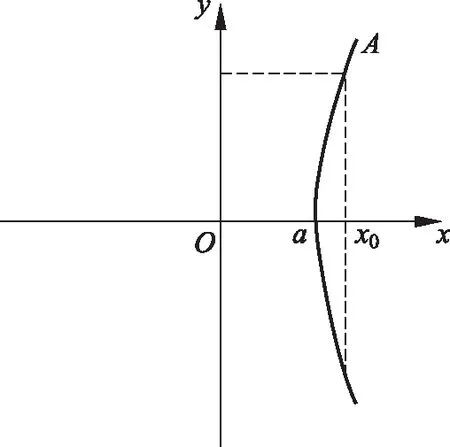
图 3

所以

由式(38)得

(44)

而S=ly0等效于平行板电容器的极板面积，d=2a两板之距，结果与平行板电容器的结果一致。

4 带电双曲面导体退化成两半无限大平面

如图4所示，当带电双曲面导体退化成相隔2a距离的两个半无限大导体平面，求该导体平面的电场分布和电荷分布。

图 4

半无限大平面可以看作是双曲面是在b→0时形成的，因此，当b→0则c→a则

(45)

由式(33)得

(46)

上式是双曲面导体上的电荷面密度。如果将上面和下面电荷量的面密度算在一起，则有

(47)

由式(25)得

(48)

方向垂直于导体平面。若用电荷密度来表示电场，则有

(49)

与预期结果一致。

5 带电双曲面导体退化成互相垂直的两无限大平面

如图5所示，当带电双曲面退化成相隔2a距离且互相垂直的一个无限大、另一个半无限大的导体平面，求该导体平面的电场分布和电荷分布。

A面，可以看作是双曲面是在b→0时形成的的半无限大平面，因此在该面上的电荷密度、电场强度还是式(47)、式(48)。

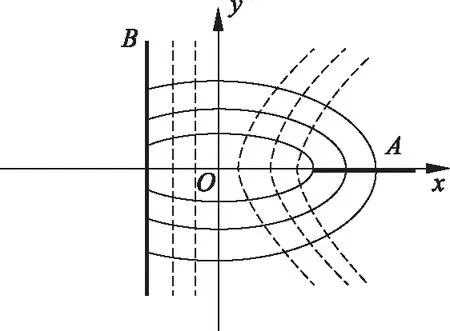
图 5

(50)

所以B面的电荷密度为

(51)

电场强度为

(52)

若用电荷密度来表示电场，则有

(53)

与预期结果一致。