基于改进体积法的高含水水平井CO2吞吐注入量计算模型
金勇,王智林,金忠康
(1.中国石化江苏油田分公司勘探开发部,江苏扬州225009;2.中国石化江苏油田分公司勘探开发研究院,江苏扬州225009;3.中国石化江苏油田分公司采油二厂,江苏金湖211600)
水平井是复杂断块油藏的主要开采方式,随着开发的进行,构造因素、井身轨迹、生产制度和外来入井会引起水平井含水率非正常上升。大量开发实践表明,注CO2吞吐是进一步挖潜高含水水平井剩余油的有效手段[1-2]。CO2注入量是水平井吞吐方案设计中最为关键的参数,决定着水平井吞吐的开发效果[3]。前人对于水平井CO2注入量的设计已经形成了多种方法,但对于物质基础相对薄弱的油藏类型,比如薄互层油藏,破碎小断块油藏,高含水油藏等(这几个特点有时还交叉存在),采用数值模拟方法需要经过地质建模、室内PVT实验、组分劈分拟合以及数值模拟拟合等步骤,研究周期长,计算繁琐,满足不了快速计算这类油藏CO2吞吐注入量的要求。因此,简单易用的工程计算公式是CO2吞吐注入量设计必不可少的工具[4-5]。目前吞吐注入量设计的工程计算方法主要采用椭圆柱体模型方法[6],该方法存在计算结果主观取值影响大,计算精度较差的问题。建立了改进柱体模型并基于多个真实区块优化结果回归了相关性系数,提升了吞吐注入量设计的计算精度,为该类型水平井CO2吞吐方案的设计提供快捷可用的工具,经现场应用获得良好的水平井挖潜效果及经济效益。
1 改进柱体模型CO2吞吐注入量公式建立
1.1 常规椭圆柱体模型方法
前人基于假设条件已经建立了水平井CO2吞吐注入量计算的椭圆柱体模型,如式(1)所示。该方法是将井周围的储层等效为一个以水平井为中心的规则椭圆形的柱体模型(图1)。则椭圆柱体模型的体积由体积公式可以计算得到,进而根据容积法确定柱体空间内赋存的剩余油的体积,对应确定所需的CO2注入量。
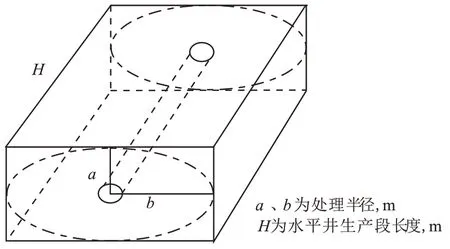
图1 水平井椭圆柱体模型Fig.1 Elliptical cylinder model of horizontal wells
该模型有其理论上的合理性,依据水平井渗流方程,均质理想水平井模型注CO2的波及范围(垂直于水平井方向的切面)应该是一个圆柱体空间。回归到实际油藏环境中,尤其是薄层油藏,在垂直方向上CO2前缘在焖井期间往往已波及至顶底边界,而水平方向尺度则大得多,使得气相波及前缘在该方向上有更远的运移空间。因此,在均质的理想中薄层油藏中,CO2驱波及的腔体可近似为一个椭圆柱体模型。这也是椭圆柱体模型计算注气量的理论基础。
椭圆柱体模型法水平井吞吐注气量设计经验公式为:

式中:Vg为地层条件下的注入CO2气体体积,m3;Pv为经验系数(0.2~0.4),无因次;φ为孔隙度,%;a、b为处理半径,m;H为水平井生产段长度,m;
由上可见,水平井CO2吞吐注入量的设计与油层孔隙度、厚度、水平段长度、处理半径和经验系数等参数有关[7]。
1.2 常规椭圆柱体模型的局限性
应用椭圆柱体模型设计水平井CO2吞吐量可一定程度上满足工程应用的需求。若要通过改进模型进一步提升公式计算的精度,扩大公式有效性的应用范围,首先要分析常规椭圆柱体模型的局限性。分析认为,常规椭圆柱体模型存在三个局限性:一是未考虑水平井跟端和趾端的“端面效应”[8]。图2为基于均质油藏中水平井的机理模型开展数模运算,焖井时间结束后的水平井周围CO2前缘的波及范围。由图2 可见,在垂直于水平方向的纵向切面上,CO2气驱前缘近似为一个椭圆形。图2b则是CO2气沿水平井方向垂向切面的波及范围,可以看出,纵向上的驱替前缘几乎在同一水平线上。但同时水平井注CO2的波及范围的跟端和趾端并不是理想的垂直于井轨迹方向的椭圆形切面,其波及范围有一定程度的“外扩”,模型计算中需要将跟端及趾端的波及范围也计算在内,改进模型中将两端的波及范围近似处理为两个等体积的椎体;二是未引入对含油饱和度的考虑。高含水水平井往往由于点状水线突进导致,不同的储层非均质性,不同的水线突进速度等因素使得其剩余油饱和度相差很大[9]。而剩余油饱和度又是CO2吞吐的“物质基础”,决定着吞吐的开发效果。椭圆柱体模型方法计算注入量其实是应用的“容积法”,借鉴容积法计算油藏储量的思路,引入含油饱和度是进一步提升公式精度的有效方法,也更具物理意义上的合理性[10];三是未针对高含水水平井的特点进行考虑。高含水率是制约该类水平井有效开发的关键因素,建立针对该类水平井的吞吐注入量计算公式应引入含水率相关的校正系数[11]。

图2 水平井CO2 吞吐气相前缘波及范围Fig.2 impact scope of the leading edge of gas phase in CO2 huff and puff of horizontal wells
1.3 改进CO2吞吐注入量计算模型推导过程
针对常规椭圆柱体模型的三个局限性,对椭圆柱体模型做出如下改进:
1)在椭圆柱体模型的两端,即水平井的跟端和趾端加入两个等效圆锥体的体积(图2b),则波及体积改进后的注入CO2体积表征为:
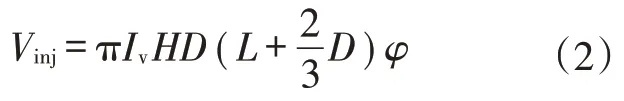
式中:Vinj为CO2注入量,m3(地层条件下体积);Iv为经验系数,无因次;H为储层厚度,m;D为垂直水平井的横向波及半径,m;L为水平井生产段长度,m;φ为储层孔隙度,%。
2)式(2)中加入水平井吞吐效果的敏感因素含油饱和度;
3)式(2)中引入对于高含水水平井的特征性质参数含水率的考虑。则注入CO2地下体积为:

式中:So为井控范围内当前平均含油饱和度,%;fw为含水率,%;n为相关性系数,无因次。
需要说明的是,石油行业对于“高含水”的定义为含水率大于60 %。因此,式(3)中基准含水率取60%和100%的中值,即80%。
筛选J油田10口已经完成三维地质建模的典型高含水水平井,分别开展CO2注入量的数值模拟优化。将储层厚度、注气横向波及半径、水平井生产长度、储层孔隙度、井控区当前含油饱和度及含水率作为自变量,CO2注入量作为因变量,经编程多元回归获得式(3)中相关性参数的取值。Iv为0.04,n为0.5。
因为现场实际注入的CO2为液态,其计量单位往往采用t,减少了地面液态CO2体积与地层条件下体积的换算过程。因此,公式中CO2注入量同样改为质量表示,改进后的水平井CO2注入量计算模型为:
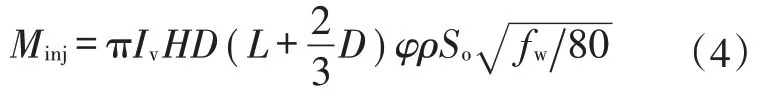
式中:Minj为CO2注入量,t(地面液态);Iv为经验系数(0.04),无因次;H为储层厚度,m;D为垂直水平井的横向波及半径(取值120 m),m;L为水平井生产段长度,m;So为井控范围内当前平均含油饱和度,%;fw为含水率,%;ρ为地层CO2密度(由密度表查得或取经验值506),103kg/m3。
其中,D经过数值模拟研究取值为120 m以进一步简化计算公式。基于相同的机理模型,开展了吞吐注入量与水平井吞吐水平方向扩散半径相关性研究。其中波及范围判定标准为:当前缘网格的含油饱和度变化大于1%,则认为该网格被气相波及。分别设计注入量为200 t、500 t、800 t、1 200 t、2 000 t五个水平。在模型属性及注采技术政策完全相同的条件下,数模运算CO2注入量对横向扩散半径的单因素影响,运算结果如表1所示。
由表1可见,总体上CO2吞吐的横向扩散半径对于CO2注入量敏感性不强。其中,当CO2注入量大于500 t 后,其扩散半径受注入量的影响程度进一步降低。当注入量从500 t 上升到2 000 t 时,其扩散半径仅增大了20 m。考虑到工程计算公式简单易用的原则,就不再将扩散半径作为注入量的因变量,而是将其取为经验值120 m。此外,注入量为200 t 方案的纵向扩散半径已经到达储层顶底边界(模型纵向厚度30 m)。因此,除非是发育巨厚油层,将气体的纵向扩散半径等同于储层厚度是可以满足大部分油藏的应用需求的。

表1 CO2吞吐注入量与气体横向扩散半径(垂直于水平井方向)关系Table 1 Relation between injection volume and transverse diffusion radius of gas(perpendicular to the direction of horizontal wells)in CO2 huff and puff
1.4 改进模型的适应性
针对水平井CO2吞吐效果的三个潜在敏感性因素,数模研究了储层厚度及渗透率对吞吐效果的影响,从机理层面讨论了含水饱和度的影响。
首先基于1.2中的机理模型,数值模拟对比了储层厚度及渗透率对吞吐效果的影响。研究表明:油层厚度小于3 m 时采油效果不好。分析认为因油层纵向厚度较小,注入气要波及相同的储层空间,沿水平井方向所需的气体波及长度要明显大于厚油层,而该距离超过了相同注气焖井时间内CO2的扩散能力。而当油层厚度大于12 m 后,累计增油量曲线增幅逐渐趋于平缓。因此,油层厚度为3~12 m的油藏是高含水水平井注CO2吞吐的最佳厚度范围。
对储层渗透率来说,随储层渗透率从100×10-3μm2增至2 500×10-3μm2,累计增油量略有增加,当渗透率增至2 500×10-3μm2时,累计增油仅增加了6.5%。可以理解为,高含水水平井储层往往为中高渗储层,这个物性级别的储层对于注气来说有很强的吸入能力,使得注入气相有足够的渗流能力达到其波及边界。即高含水(中高渗)储层中,渗透率并非注气吞吐效果的敏感因素,因此模型中并未引入对于渗透率的考虑是合理的。
从含水饱和度来看,高含水储层中CO2接触原油与在低含水储层中最大的不同在于,CO2需要穿透孔隙介质中的各种水相的赋存形态(与水膜为主)再与原油接触。室内实验表明,这个过程在实验室尺度下需要经过几到几十个小时,回到油藏环境下这个时间会更长。因此,高含水水平井的见效时间相对于普通油藏要相对晚一些。文献调研表明:虽然含水率越高,CO2接触动用原油的效果越差,但对于各个含水率水平,注CO2均能够显著提高最终采收率。即含水率越高,达到目标增油效果所需注入CO2气量越高,这个结论与模型也是相符的。
2 改进柱体模型法可靠性计算
选取J 油田典型的高含水水平井S49P1 为试验目标井,首先采用数模优化方法确定CO2吞吐注入量的最优值,通过与新改进模型的预测公式的计算结果进行对比以验证新模型的可靠性。
2.1 吞吐注入量数值模拟优化
目标区S49 断块位于SN 油田东部,探明地质储量为97×104t。S49P1井位于E2d12砂体。储层平均孔隙度23.8%,平均渗透率100.7×10-3μm2,属中孔中渗储层。地层原油密度为0.782 9 g/cm3,地层原油黏度为3.44 mPa·s,体积系数为1.125,原始气油比38 m3/t,饱和压力为5.02 MPa,是轻质常规油。
基于目标井区参数,建立如图3所示三维精细地质模型,采用角点网格系统,I方向、J方向、K方向网格数依次为110 个、47 个、38 个,对应的网格步长则为25 m×25 m×1 m。

图3 S49P1井区三维地质模型Fig.3 3D geological model of well block S49P1
在目标井真实地质模型上开展注CO2吞吐技术政策优化研究。首先比较了七种不同CO2注入量(400 t、500 t、600 t、700 t、800 t、900 t、1 000 t)下目标井在预测吞吐后三年后的采收率增加量、换油率以及综合评价指标值。其中综合评价指标为采收率增值与换油率的乘积,以综合评价吞吐的增油效果及其经济效益。CO2的注入速度为50 t/d,焖井时间为20 d,吞吐周期定为1 个周期,模拟结果如图4所示。可见采收率增量随CO2注入量的增大而逐渐上升,换油率却在不断降低。从综合评价指标可以看出,在CO2注入量达为700 t时曲线取得拐点,因此认为700 t为该油藏及开发政策条件下的最优CO2注入量。
2.2 改进柱体模型的计算结果对比
应用常规椭圆柱体模型方法及改进椭圆柱体模型新方法分别设计S49P1井吞吐注入量,将计算结果与真实模型的数模优化结果对比,结果如表2所示。
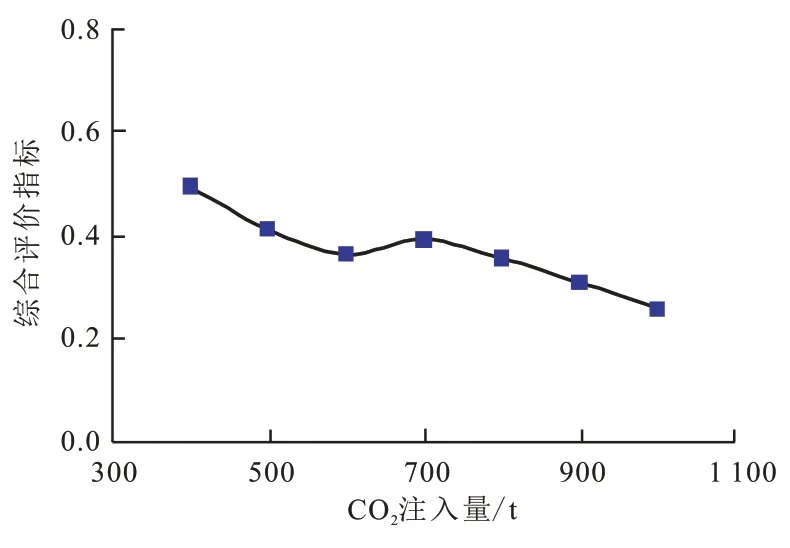
图4 S49P1井不同CO2注入量对应综合评价效果Fig.4 Corresponding comprehensive evaluation effects of different CO2 injection volume of well S49P1
由表中数据可见,改进椭圆柱体模型方法将常规柱体模型法的计算误差从92.14%降至9.29%,即预测精度大幅提升了82.85%。同时,新方法的误差在10%以内,可以满足工程快速计算的需求[12]。
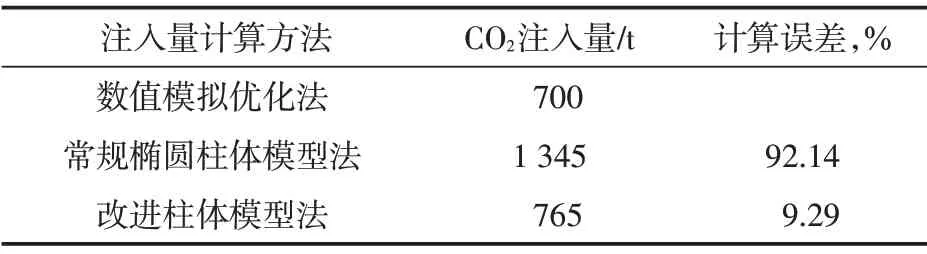
表2 三种CO2吞吐注入量设计方法计算结果对比Table 2 Comparison of calculation results of 3 design for CO2 injection volume
3 新模型计算结果应用效果
目标井S49P1 井2007年12月投产E2d12-4砂体,采用天然能量开发,初期日产油25.5 t,不含水。2012年10月下电潜泵提液,初期日产液84.4 t,日产油2.6 t,含水97%。2013年10月日产液46.4 t,日产油0.9 t,含水98.1%,11月因低产高含水而关井,累计采油33 506.8 t。该井生产情况表明,油藏天然能量充足,油井产液量较高且保持稳定,见水后含水迅速上升,随后进入低效开发阶段。
针对目标井区,依据S49P1 井区的储层物性参数,采用改进模型公式计算的吞吐注入量为700 t,按照计算结果开展现场应用。S49P1井于2017年11月3日开始实施CO2吞吐。设计注气量700 t,注气速度50 t/d,焖井时间20 d,返排速度20 m3/d。实际注入液态CO2共705 t,平均注入速度47 t/d。2017年12月9日,S49P1井结束焖井,放喷后最大日产油量5.2 t,初始含水率仅为2%。截至2018年12月26日,累积增油473 t,日产油0.5 t,日产液18.5 t,含水率97.4 %,阶段换油率0.67,增油效果显著(图5)。
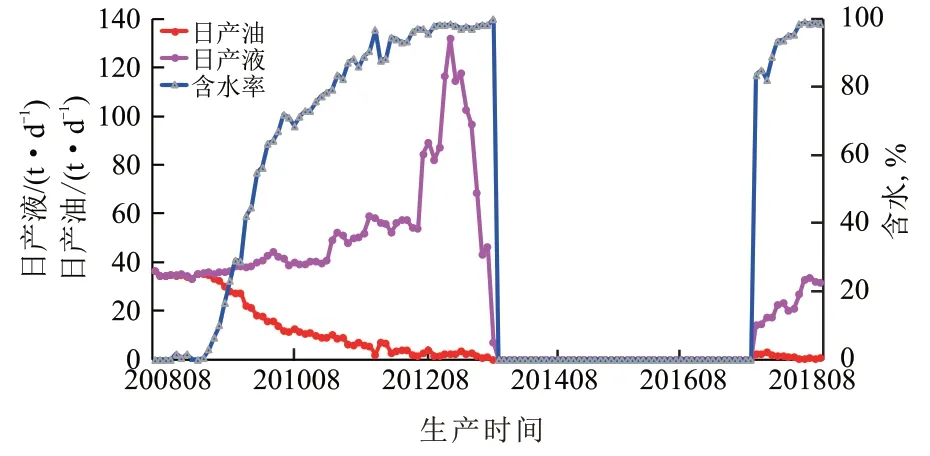
图5 S49P1井CO2吞吐前后月度生产动态曲线Fig.5 Monthly production performance curves before and after CO2 huff and puff of well S49P1
从经济评价角度来看,S49P1 井CO2吞吐作业费10 万元,注气费用22 万元,投入成本32 万元。目前已增油473 t,按油价50 美元/桶计算,实际净收益71.6万元,获得良好的经济效益。
4 结论
1)应用改进体积方法,建立了高含水水平井的CO2吞吐注入量计算模型。模型的改进主要包括:在模型预测波及体积中加入对水平井跟端及趾端“椎体”体积的计算;引入了井控范围内当前含油饱和度的影响;引入了与含水率相关的校正系数。
2)以基于真实地质模型的数值模拟优化结果为基准值,经对比表明,改进体积法的计算模型的计算结果将计算误差率由92.14%降低到9.29%,大幅提升了模型预测的吻合度,且计算精度可以满足工程设计需要。
3)应用新模型设计典型高含水水平井CO2吞吐的注入量,经现场应用取得良好开发效果及经济效益,验证了模型计算的可靠性及适应性。可为同类型水平井CO2吞吐方案的制定提供快捷且精度更高的工程计算工具。

