CO2驱油与封存中时移地震监测AVO模型研究
——以鄂尔多斯盆地低孔低渗储层为例
李丹鹭,李琳,马劲风,王浩璠
(1.二氧化碳捕集与封存技术国家地方联合工程研究中心,陕西西安710069;2.西北大学地质学系,陕西西安710069)
时移地震监测是CO2驱油和地质封存中监测CO2分布范围、确定CO2驱油波及效率,进而确定地质封存安全性的关键技术。在国际上影响力大的CO2驱油和封存项目中,加拿大Weyburn-Midale 项目(IEA GHG Weyburn-Midale CO2Monitoring and Storage Project)在Phase 1A区域开展了5次四维三分量地震监测,3 次四维VSP 在Phase1B 区域开展了四维九分量地震监测[1-3]。CO2-EOR中的四维地震监测在国际上已经有数十年历史[4],是近十年提高采收率较为有效的方法,近期监测项目包括美国Denbury 公司Bell Creek 油田的CO2-EOR[5],沙特阿拉伯的Uthmaniyah CO2-EOR[6]。而对于咸水层CO2地质封存项目,如BP石油公司在阿尔及利亚的In Salah、挪威国家石油公司的Sleipner 项目、Snovit 项目、加拿大萨省电厂与PTRC 的Aquistore 项目、欧盟在德国的Ketzin 项目、澳大利亚CO2CRC 的Owtay 项目、日本CCS 公司的苫小牧项目等,全部开展了地面四维地震监测。这其中,部分项目还辅助开展了四维VSP监测[7]。
虽然时移地震监测在国内外的很多CO2地质封存项目中获得了成功[1,8-10],但是在低孔低渗油藏的鄂尔多斯盆地,特别是陕西延长石油集团靖边、吴起区块与长庆油田黄3区块正在开展CO2驱油与封存,能否获得较好的时移地震监测效果以及时移地震监测差异的物理意义,一直未能深入的进行研究和理解。包括陕西延长石油集团在吴起油田注入CO2过程中[11]开展的三维地震监测也未能进行很好的解释[12],造成对这一区域内时移地震监测部署的质疑,和其他地质资料无法对CO2注入后的波及范围、封存效果的证实。
建立低孔低渗油藏科学的时移地震正演模型,是时移地震解释和反演的基础。而建立地震正演模型的关键,是准确确定注入CO2前后的弹性参数,特别是纵、横波速度是建立时移地震正演模型不可缺少的参数。而在CO2注入过程中,储层的温度、压力以及流体饱和度都发生了变化,对横、纵波速度造成影响,特别是CO2注入过程中和注入后难以实施二次测井而无法获得储层参数信息。因此需要科学地预测不同温度、压力和饱和度下低孔低渗储层的纵、横波速度,才能建立随注入时间变化的纵、横波速度岩石物理模型[13]。
一般来说,在注入CO2前后如果没有进行过压裂等储层改造,两次地震监测中的振幅和旅行时差异主要来自流体饱和度和压力的双重影响[14]。这种影响是储层弹性参数受流体饱和度与压力变化所致,如何预测弹性参数随CO2饱和度与地层压力变化,是时移正演模拟的关键。
CO2注入过程中流体替换的计算,采用Gassmann方程是有效的方法[4]。但是对于纵、横波速度随压力的变化关系预测,首先需要预测储层的横波速度曲线。这是因为在油田的大多数区域横波速度测井资料缺乏,需要首先预测出CO2注入前,或者测井时没有测的横波速度测井曲线。然后再考虑如何预测出注入CO2后,储层孔隙压力变化情况下的横波速度曲线。
而弹性参数随压力变化关系,可以采用岩心测试的统计结果,但是这种统计结果受到岩心测试数量和取心位置的限制,往往不反应储层的非均质性及不同孔隙度岩心随压力的变化关系,缺乏岩石物理理论的支持,不具有普遍性[14]。因此,需要建立更合理的以岩石物理理论为基础,弹性参数随压力变化的预测方法。
本研究利用考虑压力变化的Digby 模型结合Gassmann 流体替换方程进行CO2注入前后的纵、横波速度预测,然后以此为基础建立注入CO2前后的两层介质模型,制作时移AVO 梯度截距图。进而分析注入CO2过程中地层压力和流体饱和度变化对时移AVO解释的影响,为时移地震解释与监测提供依据。
1 研究区地质概况
为模拟CO2注入致密砂岩油藏中地震响应的变化,我们选择位于鄂尔多斯盆地的苏里格地区包含有黄234、黄47、黄220、盐208 四口油井的工区开展研究。其中,仅有黄47、黄234两口井有偶极横波测井资料,且黄234 井资料较为完整,其主要含油层段为三叠系上统延长组的长8-1、长8-2 段。砂体厚度约为25 m,地层压力为29.77 MPa,上覆压力为53.77 MPa。延长组厚度约110 m,主要为深灰色泥岩、砂质泥岩、碳质泥岩与灰色细砂岩、泥质砂岩不等厚互层,局部夹煤线[15]。
苏里格地区前期的储层预测研究中,对于常规横波速度预测,已有用Xu-White 方法建立的横波速度拟合模型,是用V-R-H法计算矿物的有效体积模量,Wood 模型结合Gassmann 方程进行流体替换,计算出新的横波速度[16,17]。但是这些横波速度预测方法,并不考虑储层开发过程中压力变化对速度的影响,即不是针对油田开发过程中储层压力等弹性参数变化条件下预测。因此这些方法不能用于注入CO2后,储层横波速度随压力变化的预测,也不能用于进行时移地震正演模型的建立。
2 随压力变化速度曲线预测
为预测注入CO2前初始横波速度并检验速度预测的精度,我们采用黄234 井的含油层段进行预测,并与实测纵波速度和实测横波速度进行对比。
Li 等[14]给出了以Digby[18]方法为基础的,考虑压力变化的干岩石的体变模量、切变模量以及饱和岩石的切变模量计算方法,用于砂岩储层纵、横波速度随压力变化的预测。这其中将Digby 公式中配位数Cp为常数的方法,改进为利用改进的纵波约束方法求取配位数Cp,以便适应不同地区和不同类型的储层。
Digby 公式表示干岩石的体变模量Kdry和切变模量μdry以及饱和岩石的切变模量Ksat的表达式如下:

其中:

且d满足公式(4):
其中,令:fR:U→F(V),u1→fR(Ui)=(ri1,ri2,…rim)∈F(V),rij=R(Ui,Uj),i=1,2,…,n,j=1,2,…m,则fR就是U到V的模糊影射。
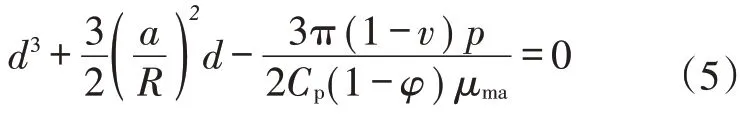
其中:Kdry与μdry分别为干岩石的体变模量和切变模量;μma为岩石骨架的切变模量;φ为孔隙度;Cp为配位数;p为差异压力,即上覆压力与孔隙压力之差;α为变形之前接触区域的半径,mm;b为变形之后接触区域的半径,mm;R为颗粒的半径,mm;v为某种介质的泊松比,比如骨架的泊松比,干岩石的泊松比等;K和μ为介质的体变模量和切变模量。
在使预测的纵波速度Vppredicted和实际纵波速度Vpmeasured误差最小条件下,获得最佳配位数Cp。

然后,将从上试计算获得的最佳配位数CP代入公式(1)(2)和(3),求得对应的干岩石的切变模量Kdry、体变模量μdry和饱和岩石的切变模量Ksat。再将这些弹性参数代入速度公式[19],则可以得到预测的横波速度和纵波速度:
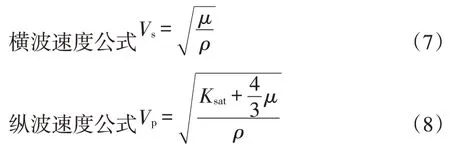
在保持原始压力和饱和度不变的状态下,利用Digby 模型结合Gassmann 方程计算出的黄234 井横波速度与实测值对比,平均误差为2.43%;预测的纵波速度与实测相比误差为0.6%(图1)。说明用Digby公式计算的体变模量Kdry和切变模量μdry较为准确,以此计算出的速度误差较小。同时由于上述方法考虑了压力和流体饱和度共同的影响,我们将之用于模拟CO2注入过程中压力变化情况下的时移地震模型建立。

图1 黄234井实际速度、预测的速度及其误差Fig.1 Actual velocity,predicted velocity and the error of well Huang-234
3 压力和饱和度变化对岩石速度参数的影响
在模拟CO2注入致密油藏提高石油采收率与地质封存的过程中,随着CO2的高压注入,地层压力也会发生变化,影响干岩石的剪切模量、体积模量和密度发生变化,因此不仅需要预测注入CO2后横波速度随压力的变化,同时还需要预测纵波速度随压力的变化。
在上一节纵波速度约束下的配位数CP计算的基础上,结合测井资料获得的矿物体变模量Kma、矿物切变模量μma、骨架泊松比v,可以分别计算出在不同地层压力和CO2饱和度下对应的混合流体密度和混合流体体变模量Kfl,再代入公式(1)—(3)得到干岩石的体变模量和切变模量。结合Gassmann方程(7)、(8),得到对应流体饱和度和压力状态下的纵波速度和横波速度。
根据研究区已有的测井数据资料,以黄234井油层段2 469.0~2 470.9 m,2 510.5~2 519.4 m,2 521.8~2 530.4 m,2 536.0~2 541.3 m 为储层。我们对储层原始的纵波速度、横波速度、密度、孔隙度、含气饱和度、泥质含量等测井岩石物理数据进行方波化处理,得到表1模型数据。
引用表1中的储层模型数据,利用上述速度模型建立方法,对油层进行压力相同、CO2饱和度变化的流体替换和速度预测。为简单起见,假定为储层仅为CO2和油两相流体,不考虑含水。那么研究区油井黄234 的原始CO2饱和度为0,故取0%,5%,10%,15%,20%,25%,30%7种饱和度,研究不同饱和度下弹性参数的变化趋势,如图2。从图中可以看到,随着CO2饱和度的增加,纵波速度减少约0.05 km/s,横波速度增加约0.000 1 km/s,基本保持不变。
考虑到研究区有效压力(上覆压力—地层压力)为24 MPa,注入压力一般应该小于盖层破裂压力。所以我们针对不同情况模拟原始地层压力增加(注入时)或减小(抽采时)5 MPa范围内进行变化。每变化1 MPa分别进行流体替换,计算对应的横波速度和纵波速度。从图3可以看出随地层压力增加,纵波速度减少约0.23 km/s,横波速度减少约0.15 km/s,速度随地层压力的改变变化显著。随着CO2的注入,必然伴随压力的改变,进而影响横、纵波速度明显变化,因此对压力影响的研究在时移地震监测中尤为重要。
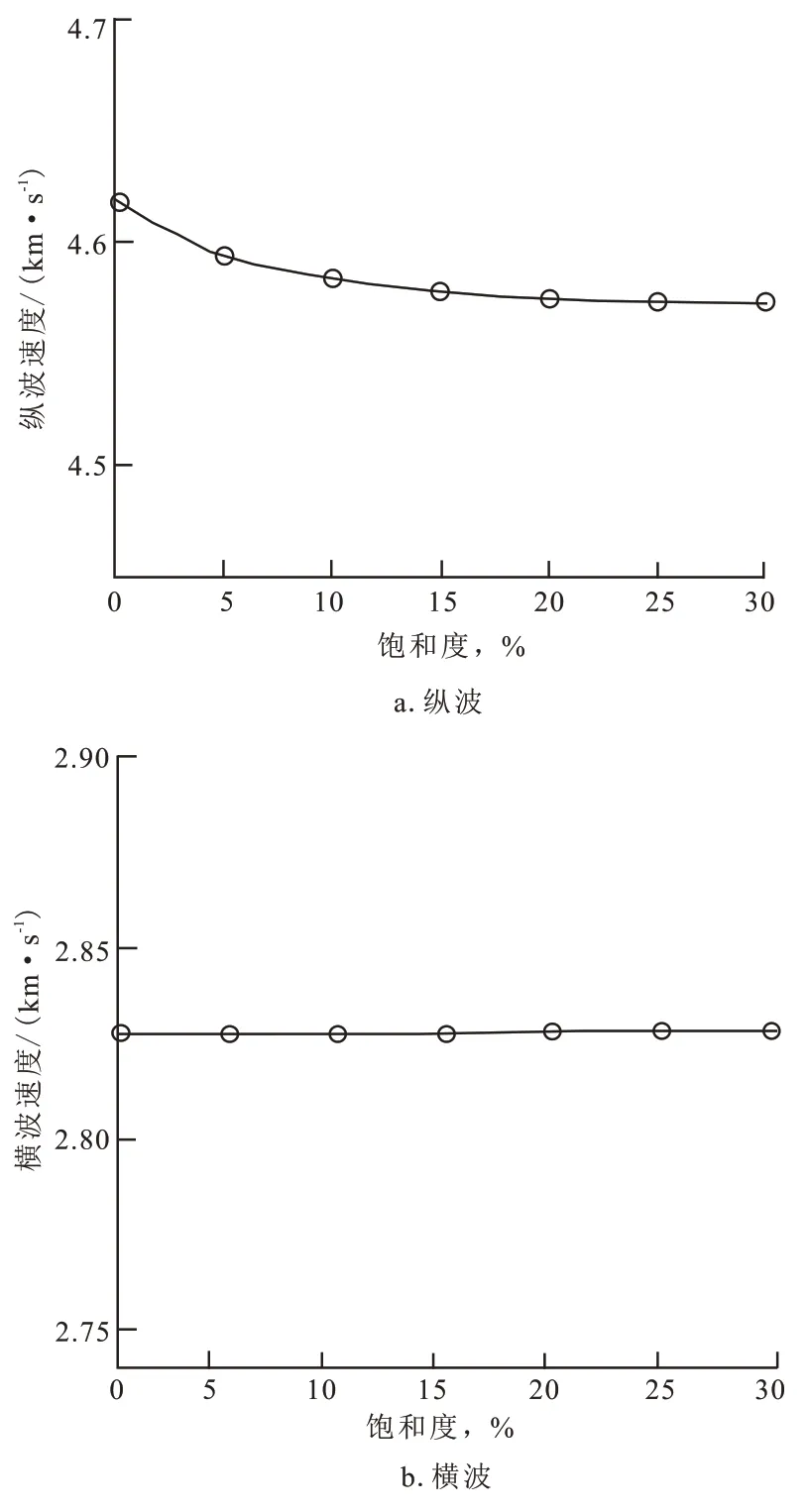
图2 同一压力状态下随着饱和度变化纵波速度和横波速度的变化趋势Fig.2 Variation trend of p-wave velocity and s-wave velocity varied with saturation under the same pressure
在实际时移地震监测过程中,不同的压力可以对应抽采和注CO2过程中地下不同的状态。如果储层孔隙压力低于原始压力,岩石速度模型可以反映抽采阶段地下压力降低。当进行CO2地质封存的过程,即地下地层压力一般是由于抽采造成低于原始压力。随着CO2注入量增加,地层压力升高至原始地层压力,再至高于原始地层压力(图3)。也可根据速度模型,模拟不同地层压力和CO2饱和度时的地下状态。
对比CO2饱和度和压力变化对致密砂岩储层速度的影响可得(图2、图3),压力是注入阶段引起横波速度变化的主要原因,其主要是通过干岩石的切变模量影响速度变化。因此,在本地区致密储层CO2驱替过程中的时移地震监测中,时移地震属性差异的变化应该主要来自压力变化的影响。

表1 黄234井模型参数Table 1 Parameters of velocity model of well Huang-234
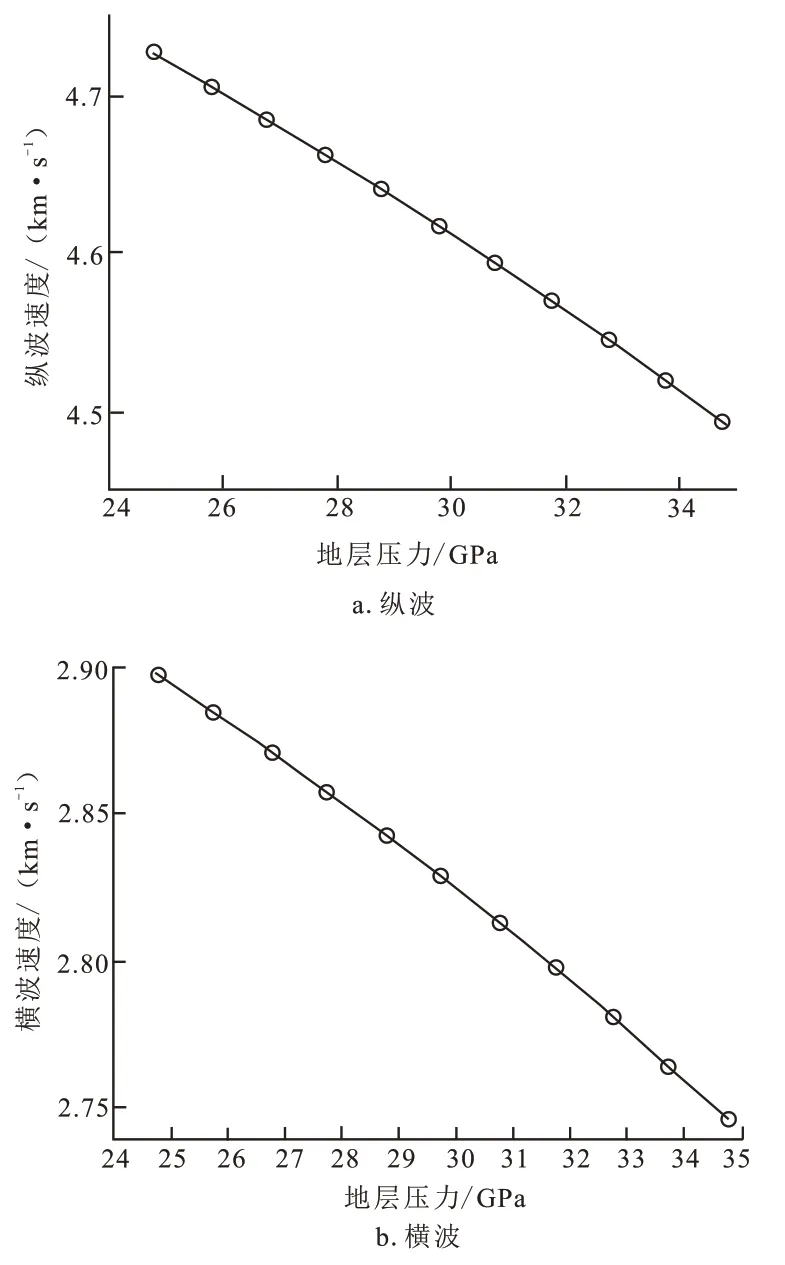
图3 同一饱和度下随着地层压力变化纵波速度和横波速度的变化趋势Fig.3 Variation trend of p-wave velocity and s-wave velocity varied with formation pressure under the same pressure
4 两层介质模型时移AVO分析
由于研究区储层较薄,横向变化大,且为砂泥岩薄层,多层模型AVO受岩层结构影响比较大,不能较好反映单纯储层注入CO2后的岩石物理性质变化。因此我们在这里开展两层介质模型,储层注入CO2过程中时移AVO[20]变化曲线。我们以黄234井含油储层和盖层为基础建立两层介质模型。对黄234 井油层上5 m 厚度盖层数据进行方波化处理,并假定注入CO2压力条件下盖层弹性参数不变,得到表2。储层数据为根据表1为基础的储层速度模型计算出的不同地层压力、CO2饱和度状态下的纵波、横波速度和密度。
首先,在原始地层压力下,取CO2饱和度分别为0%,10%,20%,30%时,含油与含CO2两相流体,进行AVO 分析(图4)。整体上反射系数随着入射角的增大,反射系数呈降低的趋势。其中黑色实线为未注入CO2原始状态,其他线为流体替换后不同饱和度下的AVO曲线。可以看到,随着CO2饱和度的增加,反射系数逐渐减小,并且饱和度越大变化越不明显。即反射系数对微小的CO2饱和度很敏感,但是随CO2饱和度增加,不同饱和度之间反射系数差异不明显。这与致密含气储层AVO特征极为相似。

表2 黄234井两层介质模型盖层参数Table 2 Cover layer parameters of two-layer model of well Huang-234
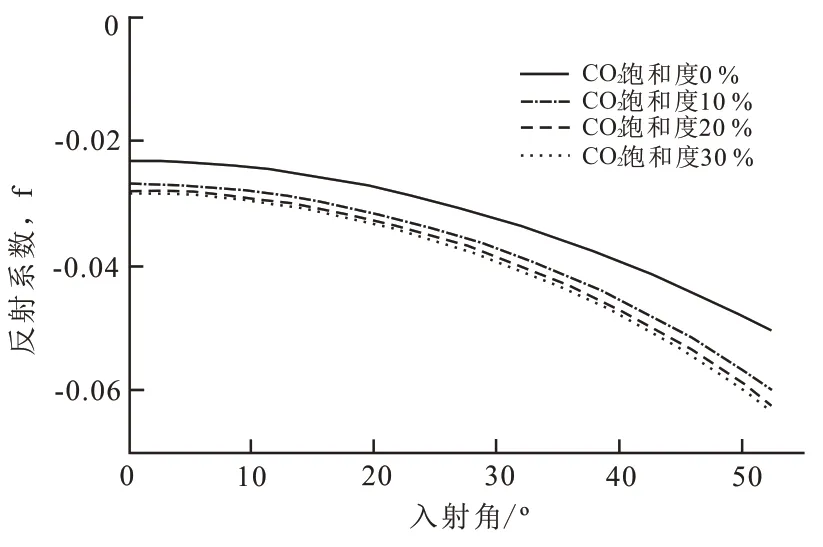
图4 随CO2饱和度变化的AVO曲线(地层压力为29.77 MPa)Fig.4 AVO curve varied with CO2 saturation(when the formation pressure is 29.77 MPa)
其次,控制CO2饱和度为0不变,每隔2 MPa改变地层压力±6 MPa,绘制AVO 曲线(图5)。对比饱和度变化和地层压力变化的AVO 曲线,可以看到反射系数对地层压力变化更为敏感。
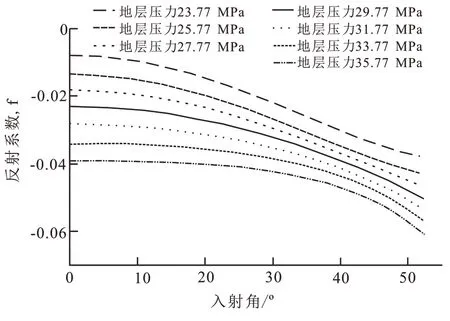
图5 随压力变化的AVO曲线(CO2饱和度为0)Fig.5 AVO curve varied with pressure(when the CO2 saturation is 0)
同时,利用Shuey[20]公式计算AVO 梯度和截距,建立梯度和截距交绘图。我们分别取上述4 个饱和度和地层压力±6 MPa 的纵波速度、横波速度和密度进行计算,得到的梯度和截距均为负值,符合第Ⅲ类含气砂岩的类别[21,22]。这同时也说明了注入地下储层的超临界CO2,其地震响应与天然气特征类似,而第二类含气砂岩是鄂尔多斯盆地最容易被常规地震技术检测到的含气储层。
图6和图7是CO2饱和度和压力分别变化的梯度截距图,星形是原始储层状态时的梯度和截距。可以看出,随压力变化时的AVO 梯度和截距变化非常明显。这说明了致密含油层注入CO2后,与注入前的地震振幅差异随注入压力增加而显著增加,采用时移地震技术可以很好地监测到注入后地震振幅的差异。而振幅的差异变化对于CO2饱和度的依赖不高,主要是地层压力变化的反映。
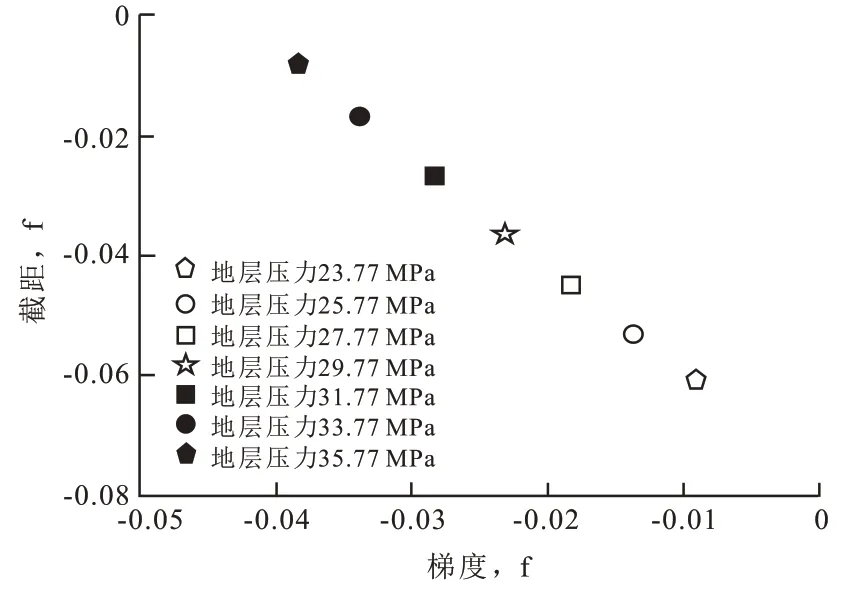
图6 随压力变化的梯度—截距(CO2饱和度为0)Fig.6 Gradient and intercept varied with pressure(when the CO2 saturation is 0)
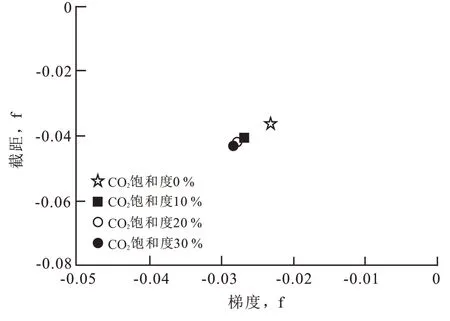
图7 随CO2饱和度变化的梯度—截距(地层压力为29.77 MPa)Fig.7 Gradient and intercept varied with CO2 saturation(when the formation pressure is 29.77 MPa)
5 结论
1)建立致密砂岩储层岩石物理模型是时移地震监测的基础。时移地震岩石物理模型的建立,关键在用横波速度的预测,以及CO2注入后储层纵、横波速度随压力变化的预测。
2)利用Digby 模型结合Gassmann 方程进行横波速度和纵波速度曲线预测,在以苏里格地区黄234油井进行检验,验证了计算体变模量和切变模量方法的高精度。同时,本文方法可以模拟纵、横波速度曲线随注入压力变化的关系。
3)以黄234井含油储层及盖层为基础建立的两层介质模型,模拟不同地层压力以及流体饱和度下的纵波和横波速度变化。揭示了随CO2注入过程中地层压力增大或CO2饱和度增大,纵波速度和横波速度均降低,压力对地震特征的影响远大于CO2饱和度的影响。两层介质模型的方法也可以应用于多层介质模型及井模型的时移AVO模拟。
4)模拟不同注入压力与饱和度变化的AVO 梯度截距图,清晰地反映了随CO2饱和度增加,纵波速度略减小,横波速度略微增加;随注入压力增加,横、纵波速度均明显减小,注入CO2后储层的AVO 特性呈现第二类含气砂岩特征。证明了CO2注入致密储层后的不同阶段,都可以采用时移地震进行有效监测。

