动物基因组选配方法与应用
何俊,Fernando B. Lopes,吴晓林,,3
动物基因组选配方法与应用
何俊1,Fernando B. Lopes2,吴晓林1,2,3
1. 湖南农业大学动物科技学院,长沙 410128 2. 美国威斯康星大学动物科学系,威斯康星州麦迪逊市 53706 3. 美国纽勤公司生物信息与生物统计部,内布拉斯加州林肯市 68504
基因组选择(genomic selection, GS)是利用覆盖基因组的分子标记预测动物个体的估计育种值,可以提高选择的准确度和选择强度,缩短世代间隔,做到早选、准选,使动物育种发生了巨大变革。过去的10多年间,基因组选择技术应用于奶牛等动物的育种中,使种用动物的选择更为准确,遗传进展得到大幅提高。但基因组选择通常重视目标性状的遗传进展,而忽略了配种亲本个体间的遗传关系,因此也没有考虑到后代群体中近交程度的增加、遗传多样性的降低以及有害基因的纯合等问题,因此难以维持长期的遗传进展。2016年,一种具有可持续性的遗传选择方法被正式提出,称为基因组选配(genomic mating, GM)。该方法利用待选种用个体的基因组信息实施优化的选种和选配,可以控制群体近交的增长速率,实现长期且可持续的遗传进展。因此基因组选配方法比基因组选择的方法更适合于现代动物育种,尤其适用于地方品种的保护和遗传改良。本文综述了基因组选配的基本概念、方法和应用,并通过模拟的方法比较了6种选配方案的选择效果,旨在为动物育种方法的应用提供参考。
基因组选择;基因组选配;优化贡献选择
动物育种方法在过去的100年间经历了巨大变化[1],其中一个革命性的转变是利用表型和系谱资料,通过最佳线性无偏预估(best linear unbiased prediction, BLUP)的方法估计育种值(estimated breeding value, EBV)[2],在此基础上进行选种和选配,提高动物的生产水平[3~6]。21世纪初,基因组选择(genomic selection, GS)技术的应用再次革新了动物育种方法[7~11]。美国农业部于2009年1月首次正式发布了荷斯坦牛(Holstein)和娟珊牛(Jersey)的基因组评估结果,同年8月又发布了棕色瑞士牛(Brown Swiss)的基因组评估结果;2013年和2016年又分别发布了爱尔夏牛(Ayrshire)和根赛牛(Guernsey)的基因组评估结果,并将基因组评估结果正式纳入种公牛的选择指标。美国农业部的研究表明,将基因组遗传评估整合到传统的评估系统中,美国Holstein重要经济性状的遗传进展速度提高了1倍,并显著降低了世代间隔和后裔测定成本,提高了选择的准确性,并可在选种时识别和淘汰携带隐性致死基因的个体[12]。中国于2008年启动了奶牛的GS研究,2012年正式将GS技术应用于荷斯坦奶牛的遗传评估:共评估了14个性状,其中产奶性状基因组预测准确性为0.59~0.76,比传统BLUP方法提高了0.13~ 0.30[11]。
但是,GS与表型选择或依据EBV的选择一样,仍然是一种截断式选择(或淘汰选择)。GS是依据基因组估计育种值(genomic-estimated breeding values, GEBV)或利用GEBV构建的选择指数,淘汰低于选择阈值的个体,选留GEBV或选择指数高于选择阈值的个体来繁育下一代[13~15]。虽然GS可以显著提高选择反应,但高产动物往往具有很高的亲属相关性,导致近交系数的快速增加和群体遗传变异度的大幅度降低。所以,如果长期采用GS,遗传进展在后续世代中反而会急剧下降[16]。
基于长期的遗传选择考虑,选择的目标应在一个多性状的系统里保持可持续的遗传进展,同时在一定范围内维持群体的遗传变异和近交水平[17]。此外,避免有害基因的纯合以及稀有基因的丢失,也需要统筹考虑[18],但这些是优化选配的问题。20世纪后期,一些研究者利用系谱关系提出了实施优化选配的方法。这些方法在寻求遗传进展最大化的同时,也限制亲本间的亲缘关系[19,20],如优化遗传贡献选择(optimal contribution selection, OCS)的方法[20]。OCS方法利用待选种用动物的系谱资料,通过使亲本加权遗传价值的最大化,同时限制彼此之间的亲缘关系,从而可以为遗传选择提供可持续、长期的遗传进展[19~22]。Woolliams等[23]提出的遗传贡献理论是OCS方法的理论基础,该理论认为,当亲本个体实际的孟德尔抽样(Mendelian-sampling)与其对后代群体的遗传贡献之间存在一定阈值线性关系(threshold-linear relationship)时,可以在约束亲本间关系的前提下实现遗传进展的最大化,但基于系谱资料估计的阈值线性关系只是近似的[21,24],因为系谱资料不能提供亲本实际的孟德尔抽样,而是其期望值或概率平均值[21,25,26]。随着基因组分子标记(如SNP)的广泛应用,基因组选配(genomic mating, GM)方法应运而生[27,28]。GM可以利用基因组信息来追踪染色体片段的遗传,从而提高对亲本孟德尔抽样估计的准确性及其与亲本遗传贡献的关系。
本文综述了利用基因组信息优化选配的基本理论、方法和应用,并通过模拟研究,比较了6种不同选配方案的效果,以期为GM技术的推广和应用提供参考。
1 优化选配的方法
1.1 基于系谱的优化选配方法
以系谱为基础,可以使用一些简单方法进行选配,如顺序选择最不相关的个体选配[29]。线性规划是较早被用来进行优化选配的方法之一[30]。线性规划使用同时求解,而不是顺序求解来避免存在相关,并找到不太相关的对子进行选配。OCS方法在统计上属于非线性规划的方法,该方法预估待选种用动物个体的最优后代数量,并确认其是否选留下来繁殖下一代。优化的方法是在维持群体遗传多样性和近交的同时,尽可能实现遗传进展的最大化,群体多样性和近交则通过基于系谱的加性遗传关系矩阵来衡量[20,21]。OCS可以用于具有重叠和非重叠世代的群体,对于具有重叠世代的OCS,需要定义各年龄段在群体中的百分比,且数据中要包含来自具有非零贡献的所有年龄段的个体。
设为基于系谱的加性遗传关系矩阵,为随机交配方案中个体对下一代的遗传贡献比例向量。如果给定向量的值,平均的加性遗传相关可以计算为:=(1/2)¢。设为后备候选个体的EBV向量(即BLUP估计的EBV),则下一代预期的遗传进展(即后代的平均EBV)为=。若育种目标是获得预期遗传进展的同时保持遗传关系增量的最小化,该选配问题可表示为:

(1)
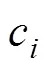
1.2 基于基因组信息的选配方法
Sonesson等[27]在OCS方法中用基因组遗传关系矩阵()替换了基于系谱的加性遗传关系矩阵()。从理论上讲,基于系谱的矩阵是假设有限位点的平均关系,代表了真实遗传关系的期望值。由于繁殖过程中的孟德尔遗传抽样,基于系谱计算的加性遗传关系与实际的亲缘关系存在差异[32]。而矩阵中的基因组遗传关系是实现了的遗传关系,反映了繁殖过程中实际的孟德尔遗传抽样,因此更为准确。此外,使用矩阵可以避免系谱错误或缺失,以及计算矩阵时忽略久远世代所造成的偏差等问题[29]。
将式(1)中的亲缘关系矩阵替换成基因组关系矩阵,将EBV估计向量替换成GEBV向量,就可以实施基因组选配:
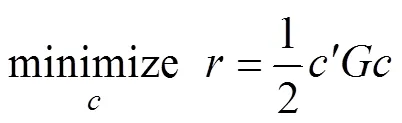
(2)
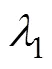
Akdemir等[28]提出的方法中,将近交控制和风险指标结合起来实施GM。其计算公式如下:
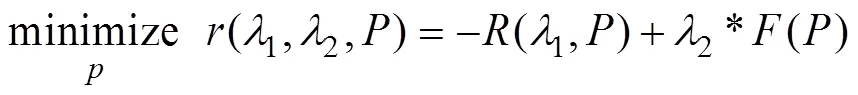
式中2≥0,是控制后代近交程度的参数,最小化配种矩阵是N×的矩阵,其中为亲代数目,N为子代动物个体的数目。1是控制等位基因杂合度的参数,该杂合度是按照标记效应加权的杂合度。2控制等位基因多样性。当1=0时,风险估计与总预期进展相同。公式(3)中的近交项()为:
其中为孟德尔抽样方差。公式(3)也可用二次优化的方法表示如下:
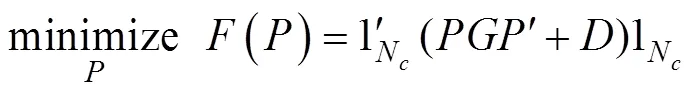
由此可知,育种方案的优化决定于家系内EBV的变异中包含了多少孟德尔抽样效应。GEBV解释的孟德尔抽样方差大致相当于小规模的后裔测定,父系和母系效应(家系间)解释了GEBV中的大部分变异,所以近亲的信息对GEBV有贡献[33]。
2 优化选配方法的应用
2.1 基于系谱优化选配的研究应用
Weigel等[34]在荷斯坦牛(Holstein)和娟珊牛(Jersey)中发现实际配种和随机交配的近交程度类似,表明当前畜群中避免近交的选配可能是无效的。采用线性规划选择种公牛并进行选配,当选配计划考虑公牛并固定近交在群体现有实际水平时,荷斯坦牛和娟珊牛的近交系数分别降低了1.6%和1.9%。当配种计划同时考虑公畜的选择和选配时,可提高养殖效益。与不考虑近交的方案相比,限制近交系数在固定水平(Holstein为5%,Jersey为8%),关注平均净利润最大化的方案,使群体近交程度下降了0.9%和1.4%,而终生利润分别增加16.66美元和26.86美元。调整近交系数的水平后,考虑平均终生利润的最大化,群体近交程度降低了1.8%和2.8%,并使Holstein和Jersey的终生利润分别增加了37.37美元和59.77美元。该研究还发现,追溯到1985年的系谱估计的近交系数,不能充分预测溯源到1960年的系谱估计的近交系数。除非获得广泛的历史系谱数据,否则选配程序不能发挥应有的作用,特别是选择种公牛[34]。
在众多的优化选配方案中,OCS方法被广泛采纳,也是目前动物育种中比较受欢迎的优化方法[20]。该方法的目标是使长期选择的遗传进展最大化,同时维持群体的种群多样性和近交程度。OCS可以有不同的计算求解方案,可利用拉格朗日乘子计算所有候选个体对下一代的最佳贡献,在预设的基于系谱的近交系数下最大化遗传进展。该方法自提出以来得到了很多改进,以考虑繁殖的限制条件为例,如限制种用繁殖个体的数量,以及对个体繁殖的遗传贡献率设置上限或下限。Meuwissen[35]提出了一个迭代启发式算法,可以处理额外的约束条件,解决原始方案中贡献太低个体的淘汰和设置遗传贡献率的上限,同时可以重复优化选留个体繁殖的遗传贡献率[36]。或使用半定规划的方法来处理这些约束条件,使遗传进展更高,但计算模型也更复杂[37,38]。另一种优化选配的方案是最大化遗传进展和近交的加权指数[33,39]。采用通用性的启发式算法,如差分进化算法来优化加权指数[40],以满足替代或额外的目标,解决选择方案的优化性和灵活性。例如,Kinghorn[41]利用此算法将计算种用个体的贡献率问题转化为选择优化配对的问题。Mullin等[42]提出了一个复杂的分支-定界算法(branch-and-bound algorithm),计算量更大,但结果稍优于Meuwissen的算法[35]。
2.2 基因组优化选配方法的研究应用
许多研究表明,维持中长期选择的遗传进展就必须控制群体近交程度的快速提升和遗传变异的丧失[16,27,43,44]。因为不管是表型选择还是GS,都会因为近交程度的提升和遗传变异的降低,长期的选择反应都会快速降低。特别是GS导致快速遗传进展和高近交增量的相关,使近交控制在长期选择中变得越来越重要。Pryce等[29]通过分析选配后代的预期遗传进展和近交以及隐性有害等位基因纯合子的变化情况,比较了配种方案,利用系谱、基因组和ROH信息的3种控制近交程度的配种策略的效果。结果表明配种方案中使用基因组信息是一种有效的方法,比系谱信息更能降低后代期望近交系数而对遗传进展影响最小。在获得相同遗传进展的情况下,相比于利用系谱信息,利用基因组信息可使后代的期望近交程度降低几乎2倍。Liu等[45]利用系谱和基因组信息,使用随机模拟来比较最小共祖选配(minimum-coancestry mating, MC)和最小化祖先间遗传贡献的协方差(minimizing the covariance between ancestral genetic contributions, MCAC)两种配种策略在5种育种方案中实现的近交增量和遗传进展,同时模拟了离散世代的随机交配作为参照。模拟了2000个QTL控制的单性状,对动物进行截断选择,选择之前,对所有后备个体进行表型测定。选择依据是岭回归模型预测的GEBV。研究结果表明,利用基因组信息时,MC和MCAC选配策略估计的近交增量比利用系谱信息的低6%~22%,而不影响遗传进展,且两种策略的近交增量和遗传进展差别不大。然而,与随机交配方案相比,在利用基因组信息的MC和MCAC选配策略下,估计的近交增量比随机交配方案低28%~44%,遗传进展提高14%。因此,利用基因组信息进行选配,可以有效控制近交增量,同时保持较高的遗传进展。
从优化选配的角度,用基因组分子标记估计个体间的遗传关系,比基于系谱估计的遗传关系更为准确和可靠。因此在OCS方法中,同样可以用基因组关系矩阵替代基于系谱的加性关系矩阵来优化选配,这就是基因组OCS方法(genomic optimal contribution selection, GOCS)[27,36]。GM比GS更完整地利用基因组信息,并强化了选配个体的互补性。GM目标函数中可包含群体遗传方差,遗传进展和近交等计算项,以考虑包含具有更高估计遗传方差的配偶的潜在优势,对于复杂性状的遗传选择也是可行的[28]。Akdemir等[28]将经济学中的风险(有用性)概念应用于GM,将GEBV、风险和亲本间的亲缘关系综合考虑并加权,以选配最佳的亲本组合。可行的选配策略必须满足特定约束条件,并且以有效前沿面(efficient frontier surface, EFS)来优化。EFS方法可以让育种者了解配种计划的预期风险如何随近交系数而变化。优化的配种方案可增加群体内的方差,减缓近交系数和亲缘系数的提高,同时保证获得一定的遗传进展。
长期的遗传选择,还需要考虑避免有利稀有基因的丢失。Jannink[16]提出了一个加权的基因组选择(weighted genomic selection, WGS)方案,其原理是根据Goddard等[43]的方法,将稀有有利基因的效应给予更多的加权,以增加这些基因在GS中的作用。对于WGS方法的进一步扩展,包括引入一些额外的参数来平衡短期和长期的遗传进展[44]以及在固定的时间范围内动态减少对稀有有利等位基因的压力[45]。此外,还有一些其他的加权方案也可以纳入考虑[46]。在GS中,除了放大有利稀有基因的效应外,还可以尝试有效的直接控制选择个体中的稀有等位基因频率以累计一些已知的QTL[47]。这可以通过构建综合QTL基因效应和遗传变异(多样性)指标的加权系数来实现。以上研究表明,通过避免稀有有利等位基因的丢失,可以最有效地使长期的遗传进展最大化。WGS增加了稀有基因效应在GS中的作用。GOCS则限制了选择的候选个体之间实现的基因组遗传关系。与GS相比,WGS和GOCS这两个方法都可以有效降低近交增量,并获得更高的长期选择的遗传进展。然而,这两个方法各有利弊。GOCS不能直接控制与选择性状相关的近交增量组分,因此无法达到遗传进展和近交控制之间的最佳平衡,特别是在选择的早期世代,遗传进展和遗传多样性的降低还没有发生很大冲突时,其效果可能比较差。而WGS虽然在一定程度上控制稀有等位基因频率,但仍然是一个截断选择,不符合优化选配的原则。Beukelaer等[18]构建了一个综合遗传进展和预期杂合度(IND-HE)或维持稀有等位基因(IND-RA)的选择指数,并使其最大化。结果表明,考虑稀有基因的方案要优于GOCS和WGS。但他们的研究结果来源于模拟数据,仍需要在实际育种中加以验证。从理论上讲,对于稀有基因的维持,也可作为一个条件加入到Akdemir等[28]提出的GM的目标函数中加以考虑。
3 不同选配方案的效果比较
使用QMSim软件[48]按照世代向前更替的方式,通过计算机模拟产生一个LD水平与真实肉牛群体非常接近的群体[49]。各世代的有效种群大小保持恒定(=1000个体,其中公母各500头)。配种1000代以后,将从1000逐渐减少到200 (公母数量相等),直至超过1020代,产生瓶颈世代。通过以上模拟策略,建立初始的突变-漂移平衡,并在基因座之间产生LD。
从瓶颈世代的最后一代,模拟一个公母牛各100的群体,采用随机交配和随机选择的方式生产10代,每头母牛每年产一个后代,公牛后代的比例为0.5。然后从群体中抽取10头公牛与100头母牛的测定世代的群体,采用BLUP估计测定群体中个体的EBV,根据EBV的高低选择后备个体。公牛的群体年更新率为60%,母牛为20%。同时模拟了一个多基因和QTL,总遗传力为0.5,表型方差为1,QTL遗传力为0.2。模拟的基因组信息参数见表1。
个体真实育种值(true breeding values, TBV)等于QTL加性效应和多基因效应之和,表型值等于TBV加随机误差。从第10代开始使用optiSel软件包[50]进行OCS,用GenomicMating软件包[28]实施GM。前者通过优化使遗传进展和遗传多样性得以维持;后者使用GS的信息,包括考虑配种亲本的互补性和最小化近交风险的加权函数。模拟试验重复10次,结果取平均值,以降低蒙特卡罗误差。
比较了6种选配方案中的亲代和子代的平均GEBV及亲缘系数,结果见图1。这6种选配方案分别是:
(1)随机交配;
(2)亲本对于后代的贡献均等;
(3)父本GEBV最大化,同时使亲缘系数最小化;
(4)亲本(父、母) GEBV最大化;亲缘系数最小化;
(5)亲本(父、母) GEBV最大化,不限制亲缘系数;
(6)最小化亲缘系数,不考虑GEBV。
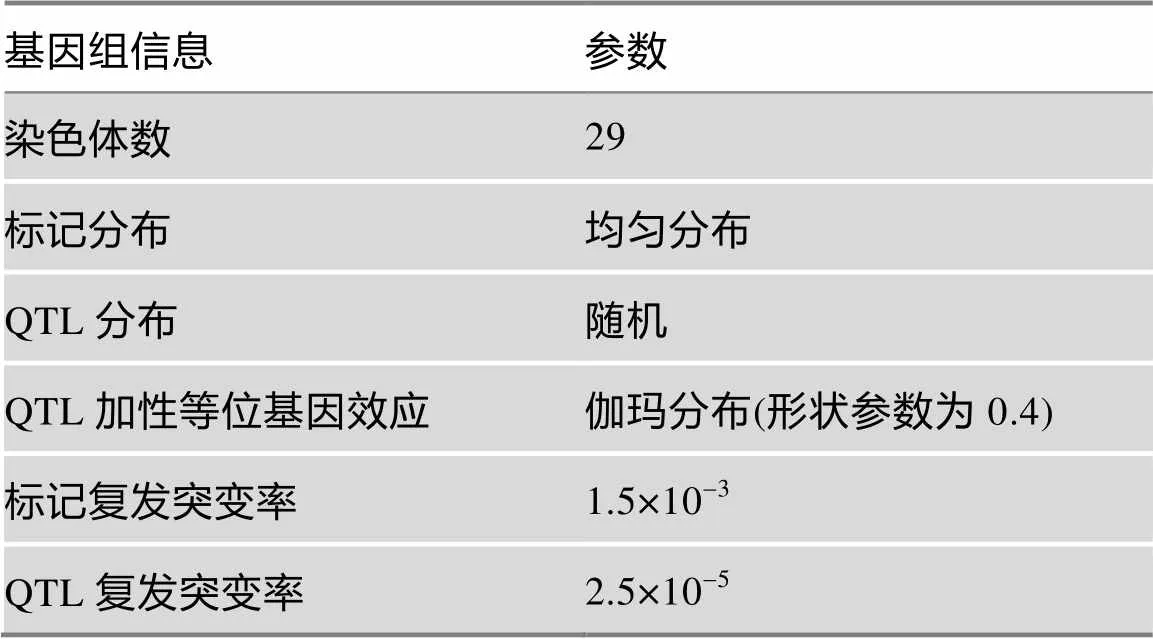
表1 模拟群体基因组信息的参数
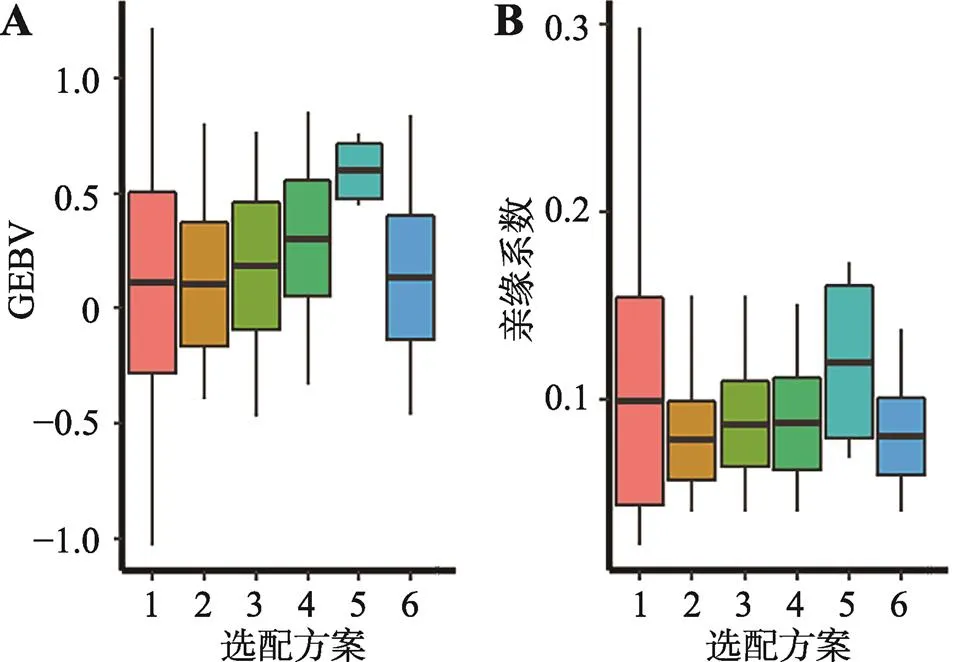
图1 不同选配方案下亲代和子代的基因组育种值与亲缘系数的比较
A:基因组育种值;B:亲缘系数。1~6代表6种不同的选配方案。
结果表明,选择亲本的GEBV最大化而不限制近交系数,其遗传进展(后代平均GEBV)最高,但该方案也显著增加了近交,因此可能带来生产和繁殖方面的问题。只选择公牛时,假设所有母牛具有相等的贡献,即每头公牛与任意一头母牛配种的概率均等。在此情形下,选择优秀公牛的同时,也可以限制近交的增加。如果选择最好的公牛和母牛配种,限制近交的增量,其遗传进展高于在限制近交的同时只选留优秀公牛的策略。亲本贡献均等的选配,近交系数最低,但是也几乎没有遗传进展,后代的平均GEBV与亲本的GEBV相当。该模拟研究结果表明,利用基因组信息的选配,可以在遗传改良经济性状的同时,有效地控制群体近交的增加。
4 结语与展望
基因组选配是一个考虑更多因素,实现种用动物的优化选择与选配的问题,既需要考虑种用动物自身的遗传,也需要考虑配偶间的遗传关系和互补性,以及一些品种特有的特征和特性,从而使群体遗传杂合度的降低、近交系数的增加以及选择世代间遗传背景基因频率的改变都最小化。因此,GM是一个非常复杂的问题。目前的研究大多考虑单一性状的加性遗传效应,对于多性状系统以及非加性遗传效应,将是未来的研究方向。此外,除了优化选配方案外,GM方法还可以应用于以下5个方面:(1)发现未知的祖先或纠正不准确的家系;(2)估计杂交动物或确认品种纯度的品种构成;(3)在基因组水平避免近交和估计非加性遗传效应;(4)发现和监测新的缺陷或经济性状的个体;(5)预测高产或低产个体出现的概率等多种情形或应用领域。
目前大多数的GM研究仍为计算机模拟研究,采用实际数据的研究和应用不多。因此,如何有效地将GM方法应用于动物的遗传改良,依然是一个需要继续探讨的问题。总之,基因组选配目前还处于初步研究阶段[28,29,44],仍然存在许多问题需要进一步的探索,如GM的优化算法,有待于继续研究和发展。此外,GM的高通量计算(high-throughput computing, HTC)也是一个需要考虑的问题,特别是对于多性状以及包括非加性遗传效应的系统。
[1] Gianola D, Rosa GJ. One hundred years of statistical developments in animal breeding., 2014, 3: 19–56.
[2] Henderson C R. Best linear unbiased estimation and prediction under a selection model., 1975, 31(2): 423–447.
[3] Vergara OD, Elzo MA, Cerón-Muñoz MF. Genetic parameters and genetic trends for age at first calving and calving interval in an angus- blanco orejinegro-zebu multibreed cattle population in colombia., 2009, 126(1): 318–322.
[4] Aguilar I, Misztal I, Johnson DL, Legarra A, Tsuruta S, Lawlor TJ. Hot topic: a unified approach to utilize phenotypic, full pedigree, and genomic information for genetic evaluation of Holstein final score., 2010, 93(2): 743–752
[5] Caetano SL, Savegnago RP, Boligon AA, Ramos SB, Chud TCS, Lôbo RB, Munari DP. Estimates of genetic parameters for carcass, growth and reproductive traits in nellore cattle., 2013, 155(1): 1–7.
[6] Lopes FB, da Silva MC, Magnabosco CU, Goncalves Narciso MG, Sainz RD. Selection indices and multivariate analysis show similar results in the evaluation of growth and carcass traits in beef cattle., 2016, 11(1): e0147180.
[7] Meuwissen TH, Hayes BJ, Goddard ME. Prediction of total genetic value using genome-wide dense marker maps., 2001, 157(4): 1819–1829.
[8] Meuwissen T. Genomic selection: the future of marker assisted selection and animal breeding. In: Proceedings of Electronic forum on biotechnology in food and agriculture. MAS: a fast track to increase genetic gain in plant and animal breeding, Session II: MAS in animals. FAO, Conference 10. University of Turin via L. da Vinci 44, Grugliasco (TO), Italy. 2003, 54–59.
[9] Goddard ME, Hayes BJ. Genomic selection., 2007, 124(6): 323–330.
[10] VanRaden PM. Practical implications for genetic modeling in the genomics era., 2016, 99(3): 2405–2412.
[11] Tan C, Bian C, Yang D, Li N, Wu ZF, Hu XX. Application of genomic selection in farm animal breeding., 2017, 39(11): 1033–1045.谈成, 边成, 杨达, 李宁, 吴珍芳, 胡晓湘, 李明洲. 基因组选择技术在农业动物育种中的应用. 遗传, 2017, 39(11): 1033–1045.
[12] Wiggans GR, Cole JB, Hubbard SM, Sonstegard TS. Genomic selection in dairy cattle: The USDA experience., 2017, 5: 309–327.
[13] Meuwissen T, Hayes B, Goddard M. Accelerating improvement of livestock with genomic selection., 2013, 1: 221–237.
[14] de los Campos G, Hickey JM, Pong-Wong R, Daetwyler HD, Calus MP. Whole-genome regression and prediction methods applied to plant and animal breeding., 2013, 193(2): 327–345.
[15] Lourenco DA, Tsuruta S, Fragomeni BO, Masuda Y, Aguilar I, Legarra A, Bertrand JK, Amen TS, Wang L, Moser DW, Misztal I. Genetic evaluation using single-step genomic best linear unbiased predictor in american angus,, 2015, 93(6): 2653–2662.
[16] Jannink JL. Dynamics of long-term genomic selection., 2010, 42: 35.
[17] Akdemir D, Beavis W, Fritsche-Neto R, Singh AK, Isidro- Sánchez J. Multi-objective optimized genomic breeding strategies for sustainable food improvement., 2019, 122(5):672–683.
[18] De Beukelaer H, Badke Y, Fack V, De Meyer G. Moving beyond managing realized genomic relationship in long- term genomic selection., 2017, 206(2): 1127– 1138.
[19] Wray NR, Goddard ME. Increasing long-term response to selection., 1994, 26(5): 431–451.
[20] Meuwissen TH. Maximizing the response of selection with a predetermined rate of inbreeding., 1997, 75(4): 934–940.
[21] Grundy B, Villanueva B, Woolliams JA. Dynamic selection procedures for constrained inbreeding and their consequences for pedigree development., 1998, 72(2): 159–168.
[22] Grundy B, Villanueva B, Woolliams JA. Dynamic selection for maximizing response with constrained inbreeding in schemes with overlapping generations., 2000, 70(3), 373–382.
[23] Woolliams JA, Thompson R. A theory of genetic contributions. In: Proceedings of 5th World Congress of Genetics Applied to Livestock Production, University of Guelph, Guelph, Ontario, Canada. 1994, 25: 127–134.
[24] Avendaño S, Woolliams JA, Villanueva B. Mendelian sampling terms as a selective advantage in optimum breeding schemes with restrictions on the rate of inbreeding., 2004, 83(1), 55–64.
[25] Daetwyler HD, Villanueva B, Bijma P, Woolliams JA. Inbreeding in genome‐wide selection., 2007, 124(6): 369–376.
[26] Henryon M, Berg P, Sørensen AC. Animal-breeding schemes using genomic information need breeding plans designed to maximise long-term genetic gains., 2014, 166: 38–47.
[27] Sonesson AK, Woolliams JA, Meuwissen THE. Genomic selection requires genomic control of inbreeding., 2012, 44: 27.
[28] Akdemir D, Sánchez JI. Efficient breeding by genomic mating., 2016, 7: 210
[29] Pryce JE, Hayes BJ, Goddard ME. Novel strategies to minimize progeny inbreeding while maximizing genetic gain using genomic information., 2012, 95(1): 377–388.
[30] Jansen GB, Wilton JW. Selecting mating pairs with linear programming techniques., 1985, 68(5): 1302– 1305.
[31] Schierenbeck S, Pimentel ECG, Tietze M, Körte J, Reents R, Reinhardt F, Simianer H, König S. Controlling inbreeding and maximizing genetic gain using semi- definite programming with pedigree-based and genomic relationships., 2011, 94(12): 6143–6152.
[32] Hill WG, Weir BS. Variation in actual relationship as a consequence of mendelian sampling and linkage., 2011, 93(1): 47–64.
[33] Clark SA, Kinghorn BP, Hickey JM, van der Werf JH. The effect of genomic information on optimal contribution selection in livestock breeding programs., 2013, 45: 44. doi:10.1186/1297-9686-45-44.
[34] Weigel KA, Lin SW. Use of computerized mate selection programs to control inbreeding of holstein and jersey cattle in the next generation., 2000, 83(4): 822–828.
[35] Meuwissen THE. GENCONT: An operational tool for controlling inbreeding in selection and conservation schemes. In: Proceedings of 7th World Congress on Genetics Applied to Livestock Production. Montpellier, France. 2002, CD-ROM communication no 28–20.
[36] Woolliams JA, Berg P, Dagnachew BS, Meuwissen TH. Genetic contributions and their optimization., 2015, 132(2): 89–99.
[37] Pong-Wong R, Woolliams JA. Optimisation of contribution of candidate parents to maximise genetic gain and restricting inbreeding using semidefinite programming., 2007, 39(1): 3–25.
[38] Ahlinder J, Mullin TJ, Yamashita M. Using semidefinite programming to optimize unequal deployment of genotypes to a clonal seed orchard., 2014, 10(1): 27–34.
[39] Carvalheiro R, Queiroz SAD, Kinghorn B. Optimum contribution selection using differential evolution., 2010, 39(7): 1429–1436.
[40] Storn R, Price K. Differential evolution a simple and efficient heuristic for global optimization over continuous spaces., 1997, 11(4): 341–359.
[41] Kinghorn BP. An algorithm for efficient constrained mate selection., 2011, 43(1): 4.
[42] Mullin TJ, Belotti P. Using branch-and-bound algorithms to optimize selection of a fixed-size breeding population under a relatedness constraint., 2016, 12(1): 4.
[43] Goddard M. Genomic selection: prediction of accuracy and maximisation of long term response., 2009, 136(2): 245–257.
[44] Sun C, VanRaden PM, O’Connell JR, Weigel KA, Gianola D. Mating programs including genomic relationships and dominance effects., 2013, 96(12): 8014–8023.
[45] Liu H, Henryon M, Sørensen AC. Mating strategies with genomic information reduce rates of inbreeding in animal breeding schemes without compromising genetic gain., 2017, 11(4): 547–555.
[46] Liu AYH, Woolliams JA. Continuous approximations for optimizing allele trajectories., 2010, 92: 157–166.
[47] Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data., 2008, 83(3): 311–321.
[48] Sargolzaei M, Schenkel FS. QMSim: a large-scale genome simulator for livestock., 2009, 25(5): 680– 681.
[49] Brito FV, Neto JB, Sargolzaei M, Cobuci JA, Schenkel FS. Accuracy of genomic selection in simulated populations mimicking the extent of linkage disequilibrium in beef cattle., 2011, 12(1): 80.
[50] Wellmann R. Optimum contribution selection for animal breeding and conservation: the R package optiSel., 2019, 20 (1): 25.
Methods and applications of animal genomic mating
Jun He1, Fernando B. Lopes2, Xiao-Lin Wu1,2,3
Genomic selection (GS) is a powerful tool which can be used to estimate the breeding value of individual animals by using the molecular markers of the animal’s entire genome. GS improves the accuracy and intensity of selection, reduces the interval of generation, and realizes the effects of early accuracy selection contributing to a significant evolution in animal breeding. In the past decade, GS was successfully applied in the genetic improvement of dairy animals with improved selection accuracy and genetic gain of breeding animals. However, GS focuses on the genetic gain of target traits while it ignores the genetic relationship between mating pairs such that it ignores long term genetic merits such as an increase in inbreeding coefficient of offspring population, a decrease of genetic diversity and the homozygous presentation of harmful genes. In 2016, genomic mating (GM) was proposed as a sustainable genetic selection method using genomic information of the breeding candidate individuals to optimize selection and mating with resultant control of the growth rate of population inbreeding coefficient and achieving long-term and sustainable genetic progress. Therefore, GM is more suitable for modern animal breeding than GS, especially for the genetic improvement of indigenous species. In this review, we summarize the basic concepts, methods, and applications of GM, and then present examples comparing the effects of six simulated mating schemes. This review serves as a valuable reference for the applications of animal breeding methods.
genomic selection; genomic mating; optimal contribution selection
2019-02-28;
2019-05-10
湖南省科技计划重点项目(编号:2018NK2081),长沙市科技计划重点项目(编号:kq1801014)和湖南省百人计划项目和湖南省畜禽安全协同创新中心项目资助[Supported by Key Project of Scientific Research Plan of Hunan Province (No.2018NK2081), Key Project of Scientific Research Plan of Changsha city (No. kq1801014) and Hundred-Talent Project of Hunan Province and Hunan Innovation Center of Animal Safety Production]
何俊,博士,副教授,研究方向:动物遗传育种。E-mail: hejun@hunau.edu.cn
吴晓林,教授,博士生导师,研究方向:动物遗传育种。E-mail: nwu@neogen.com
10.16288/j.yczz.19-053
2019/5/30 13:11:44
URI: http://kns.cnki.net/kcms/detail/11.1913.R.20190530.1311.001.html
(责任编委: 任军)

