基于多元模型融合和时延变量选择的动态软测量方法

杨仁建

(中国石化石油化工科学研究院，北京100083)

现代工业技术的不断发展对产品质量和安全生产的要求越来越严格，这就需要通过各种各样的检测仪表实现对生产过程参数的实时监控[1]。然而，由于技术或经济的原因，导致很多指标无法在线检测或者检测耗时长、滞后严重，造成产品质量不合格，带来巨大的经济损失和安全隐患[2]。因此，在线实时检测过程参数，具有重要的应用意义。

为了更好地利用时延变量优化选取和多模型预测的优势，本文提出了一种基于多元模型融合和时延变量选择的动态软测量方法。该方法一方面根据信息熵定义联合互信息指标，通过螺旋优化算法搜索得到最优的时延变量参数，另一方面将高斯模型和正则极限学习机RELM (regular extreme learning machine)相结合，综合两者的长处，引入融合更新机制，实现软测量，最终将提出的方法用于脱丁烷塔塔底的丁烷(C4H10)体积分数预测中。

1 软测量建模

针对工业过程参数检测，常用的解决方法有两种： 一是从仪器设备角度不断地研发新型仪表，提高设备的应用场景和检测精度，但是存在设备成本高、维护困难、分析周期长且滞后时间长的问题；二是通过测量与待检测参数相关联的变量，间接得到目标检测变量[3]。软测量技术通过检测易测变量，发掘其与目标变量之间的关系，构造预测模型，间接地完成对目标变量的实时估计。由于其成本低、易于实现，因此在工业过程中得到广泛采用。

图1 动态软测量建模示意

然而，工业过程参数往往具有时延和非线性等特性，常规的软测量方法难以满足预测精度。由于操作条件的变化、催化剂活性降低、机械磨损、进料成分变化以及季节变化等因素，导致原有的软测量模型将不再适应新的工况而出现模型老化现象，因此无法准确预测当前状态信息[4]。常用的动态建模方法通过将辅助变量的历史测量值(时延变量)有选择性地加入到输入中，将原始时变动态建模问题转化为静态问题，从而建立动态软测量模型[5]，常用的方法包括反馈网络建模方法、多点输入建模方法、多模型结构建模方法、动态加权输入建模方法等[6-7]。Galicia等通过选取固定长度的时延变量，引入输入建立模型，对软测量方法进行改进，但是该方法难以保证不同工况下的建模精度[8]。Osorio等采用神经网络改进软测量方法，通过将输出反馈回输入增广输入矩阵，具有较好的预测效果[9]。文献[10]提出了一种基于互信息和最小二乘支持向量机的软测量建模方法，采用互信息描述变量之间的相关性，实现了对水泥生料细度的预测。文献[11]提出了一种动态校正的多模型软测量建模方法，通过将高斯模型和高斯过程回归结合，采用自适应进行反馈校正，较好地实现了硫回收装置的体积分数估计。关于时延变量的选取，目前主要采用以下两种方法：

1)相关性分析法。文献[11—12]基于互信息对变量的相关性进行分析，同归最大互信息指标，确定时延变量的长度。

2)启发式搜索。根据时延变量建立优化模型，通过启发式搜索算法，如遗传算法[13]、粒子群算法[14]、差分进化算法[15]等，获取误差最小的时延变量维度，文献[16]通过构造合适的适应度函数，将时延变量参数估计问题转化为一个多维非线性优化问题，进而采用混合差分进化算法得到最优的时延变量个数，进行软测量建模，在常压塔航空煤油闪点预测中取得了较好的应用效果。

2 问题描述

对于一个工业过程，假设系统的数据集{x(k)，y(k)}，k∈[1，n]，其中x(k)=[x1(k)，x2(k)， …，xm(k)]∈Rm与y(k)∈R分别表示k时刻的输入和输出。考虑系统延时，对k时刻的输入进行修正：

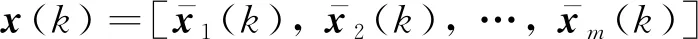
(1)

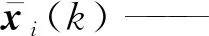
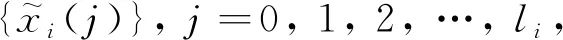
综上所述，对于给定的数据集，只需针对每个变量从候选时延变量中选取从k-di时刻开始的连续的li个主导变量，得到用于建模的输入输出数据；然后基于数据进行建模，即可得到软测量模型。针对以上情况，本文一方面提出时延变量选择策略，基于联合互信息最大化，采用螺旋优化算法寻优，得到最佳时延参数di和数据长度li，确定建模数据集；另一方面引入多元模型融合策略，将高斯模型和RELM相结合，建立软测量模型。

3 时延变量选择策略

3.1 基于联合互信息的时延变量优化

互信息能够充分地描述变量之间的相互关系，被广泛地应用于系统分析、变量选择、图像处理等方面。然而，常规的互信息估计方法计算量大，算法过程复杂、精度低，不能有效地求解高维问题。k-近邻互信息估计方法是由Kraskov等针对高维变量求解提出的互信息估计方法，具有计算简单、精度高等优点[17-18]。本文针对k-近邻互信息估计方法对时延变量进行分析。

由文献[17]可知，对于变量x，y构成的空间z=(x，y)，按照zi=(xi，yi)与其他点的距离进行排序，则定义εi/2为该点到其本身的k-近邻距离，其中εx(i)/2和εy(i)/2分别为到x轴和y轴相应点的距离。假设变量xi和yi的k-近邻距离内分别有nx(i)和ny(i)个样本点，则变量x和y的互信息可通过式(2)进行计算：

MI(x，y)=φ(k)-〈φ(nx+1)+φ(ny+1)〉+φ(N)

(2)

式中：φ(k)——双Γ函数，φ(k)=Γ(k)-1dΓ(k)/dk，其中dΓ(k)/dk表示微分，满足迭代关系φ(k+1)=φ(k)+1/k，且φ(1)≈-0.577 215 6，符号〈g〉表示对所有变量i∈[1，n]取平均，即：

(3)

针对一般问题，将式(2)拓广到m维变量，则变量(x1，x2， …，xm)的互信息可表示为

MI(x1，x2， …，xm)=φ(k)-
〈φ(nx1)+…+φ(nxm)〉+(m-1)φ(N)

(4)

k-近邻互信息估计的计算结果受参数k的影响非常大，k越大，计算结果越精确，但是计算量会大幅增加；k越小，计算量越小，但是精度相应会变差，目前尚未有合理的方法对k进行选择。本文基于k-近邻互信息估计的基本思想，基于互信息定义联合互信息计算公式：

MI(x1，x2， …，xm；y)=MI(x1，x2， …，xm，y)-MI(x1，x2， …，xm)

(5)

式中：MI(x1，x2， …，xm，y)——输入和输出变量的高维互信息；MI(x1，x2， …，xm)——各输入变量的高维互信息，两者均可由式(4)得到。

由式(5)可知，MI(x1，x2， …，xm，y)越大，参数反映的输入和输出信息越多，输入和输出之间的相关性越大；MI(x1，x2， …，xm)越小，各输入变量的相关性越小，得到的联合互信息参数MI(x1，x2， …，xm；y)越大。因此，只要求得满足MI(x1，x2， …，xm；y)最大时各输入变量的相关参数，即可确定时延变量。结合图1中给出的模型延时变量，得到如下最优化问题：

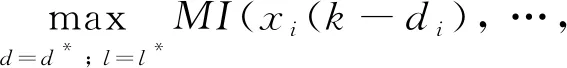
(6)

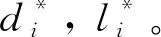
3.2 螺旋优化求解

螺旋优化算法是在模仿自然界中螺旋现象的基础上提出的，通过个体围绕中心点旋转搜索，逐步逼近最优解。文献[19]给出了一种改进的螺旋优化算法，通过引入自适应柯西变异和拉丁超立方采样，增强了标准螺旋优化的全局搜索能力，能有效得到全局最优解。

对于n维空间的优化问题，假设中心点为x*，则围绕x*的旋转可以描述为

x(k+1)=γTn(θ)x(k)

(7)

(8)

式中：T(n)(θ)——旋转矩阵；θ——围绕x*的旋转角度，且0<θ<2π；γ——收缩系数，能反应旋转前后与x*的距离变化，且0<γ<1。

假设种群大小为pop，定义每一步迭代过程中存储的个体最佳历史解Pbestij(k)和全局最优解Gbestj(k)，则自适应柯西变异定义如下：

xij(k+1)=xij(k)+αχjC(0， 1)

(9)

(10)

式中：α——校正因子；C(0， 1)——由柯西分布生成的随机数。

改进螺旋优化算法的执行过程如图2所示。

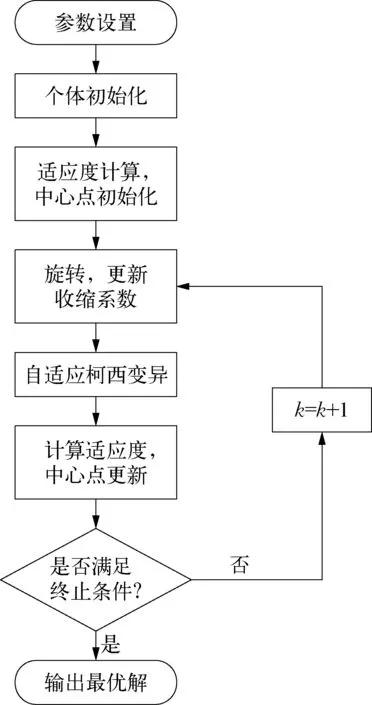
图2 改进螺旋优化算法流程示意

4 基于高斯模型和极限学习机的多元模型融合策略

对于给定的输入输出软测量建模数据，采用第2节和第3节的相关理论确定了时延参数后，得到新的建模数据集{xi(k-di)，xi(k-di-1)， …，xi(k-di-li)，y(k)}，k∈[1，n]，为了简化描述，下文中统一用{xk，yk)表示。为了提高软测量建模的精度和泛化能力，本文提出一种多元模型融合策略基于数据集进行建模预测。

4.1 高斯模型

文献[20]给出了高斯模型的基本理论，对于数据集{xk，yk}，k=1， …，n，若给定1个新的输入xn+1，则预测输出yn+1可写作：

(11)

δ2(xn+1)=c(xn+1)-c(xn+1)TC-1c(xn+1)

(12)

(13)

(14)

超参数θ可以通过贝叶斯推理进行估计，将高斯分布转化为p(y|θ，x)=G(0，C)，最大化的对数似然函数如下：

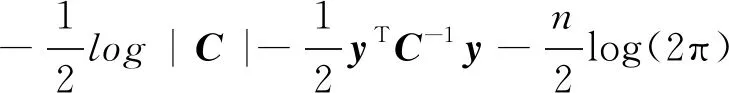
(15)

针对式(15)采用共轭梯度法求偏导数，依次求解得到各个超参数，即可确定具体的高斯模型，根据式(11)对下一时刻的输出给出预测值。

4.2 正则极限学习机

极限学习机的本质是一种单层前馈神经网络，可以通过选取输入权重和隐层偏置对网络进行逼近，能够在保证较高精度的前提下较大地加快学习速度。文献[21]给出了基于果岭回归的RELM，对于数据集{xk，yk)，k=1， …，n，可通过求解如下最小二乘解得到：

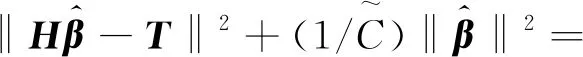
(16)

(17)

式中：H——隐层输出矩阵，它的第i列是第i个隐层节点相对于x1，x2， …，xn的输出；G(·)——激励函数；wi=[wi1， …，win]T——隐层节点和输入节点的权向量；βi=[βi1， …，βin]T——隐层节点和输出节点的权向量；bi——偏置。

求解式(16)所述的优化问题，即可得到RELM的预测输出模型：

(18)

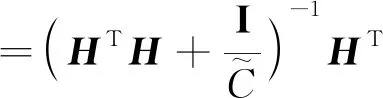
(19)

4.3 模型更新机制

对于实际的工业过程，往往受各种工况条件、人为因素、机械磨损等因素影响，导致基于一次模型预测的结果不够准确，需要不断更新模型参数，甚至更新模型。本节中，引入了模型更新机制，选取对模型有利的参数进行更新，分别针对高斯模型和RELM介绍了数据选取准则，采用递归求解的方法提高更新效率。

4.3.1高斯模型更新

高斯模型通过预测方差评价预测输出的置信水平，当方差δ(x)较小时，可认为预测输出是准确的；当方差较大时，则认为输出不准确。本节中，通过定义方差阈值δlimit(x)，选取对预测有理的样本数据，若预测方差超过阈值，则认为样本是有利的，否则，将样本剔除。

对于已知数据集，在加入新样本xn+1后，相应的输出修正为

(20)

(21)

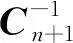
(22)

(23)

(24)

4.3.2RELM更新

由于RELM不引入预测方差，无法对预测结果进行直接评价，这里定义误差函数：

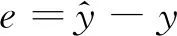
(25)

通过设置误差阈值elimit对模型进行评价，从而确定是否对模型进行更新。若误差大于阈值，则认为新样本对模型改进有利，保留；否则，删掉样本数据。

(26)

式中：Hn——初始隐层输出矩阵。

当有利样本加入训练集后，隐层输出矩阵更新为

(27)

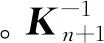
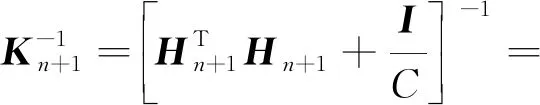
(28)

根据Woodbury矩阵恒等式[22]，式(28)可写作：

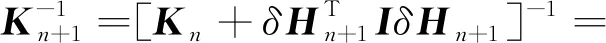
(29)

输出权重βn+1更新为

(30)

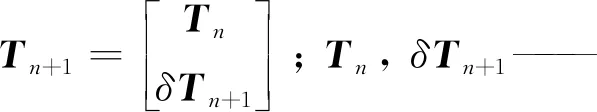
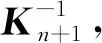
4.4 多元模型融合策略

为了提高模型的预测精度和泛化能力，本文在多模型估计的基础上，提出了一种多元模型融合策略，通过权值将高斯模型和RELM进行融合。假设模型集M={mj，j=1， 2， …，r}包含有限个模型，其中模型mj是对不同模型的描述。对于任意如下形式离散非线性系统：

(31)

式中：xk——系统状态；uk——控制变量；yk——系统输出；σk，μk——过程噪声和测量噪声，且满足σk∶N(0， Qk)， μk∶N(0，Rk)。

针对上述系统，采用多元模型融合策略进行预测的基本步骤如下：

1)条件初始化。假设k-1时刻的匹配模型是mi，k时刻的匹配模型是mj，则在yk-1条件下的融合概率为

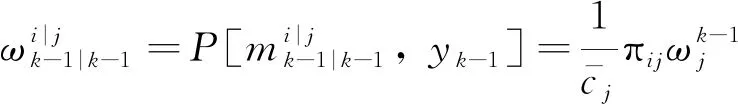
(32)

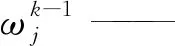
当j=1， 2， …，r时，初始化状态和协方差的融合估计为

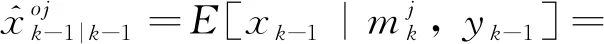
(33)

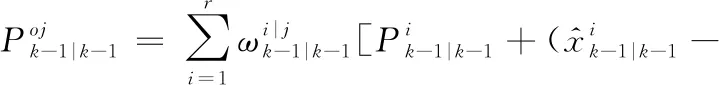
(34)

2)模型条件无迹卡尔曼滤波。采用无迹卡尔曼滤波[23]，根据步骤1)中初始化的状态和协方差，以及输出的yk更新状态估计。基于无迹卡尔曼滤波的基本公式如式(35)所示：

a)状态采样

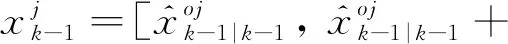
(35)

式中：n——状态的维度；λ——系数。

b)时间更新

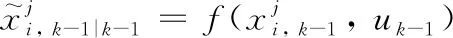
(36)

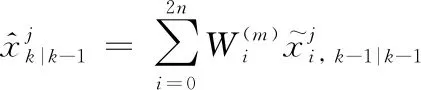
(37)

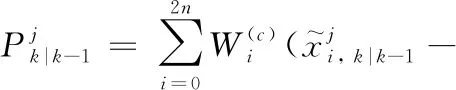
(38)

其中，各系数定义如下：

(39)

(40)

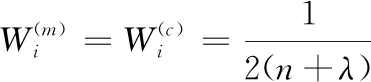
(41)

c)量测更新

(42)

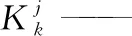
3)概率更新。模型概率计算公式如下：

(43)

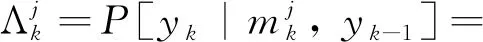
(44)

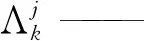
4)多元模型融合软测量建模

(45)

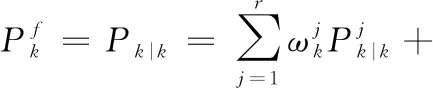
(46)

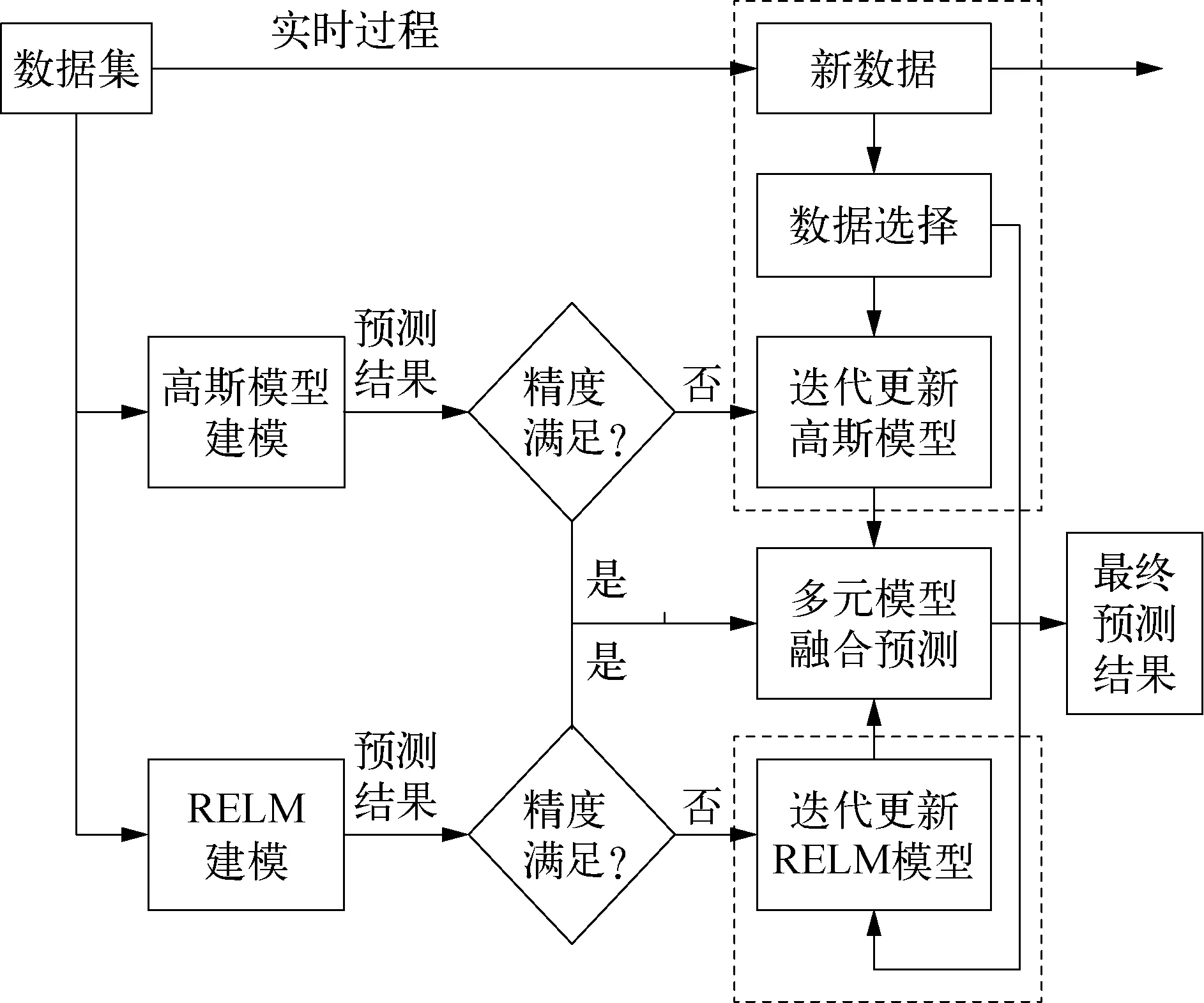
图3 多元模型融合预测过程示意

5 基于多元模型融合和时延变量选择的脱丁烷塔动态软测量

5.1 脱丁烷塔介绍

脱丁烷塔是石油炼制生产过程中脱硫和石脑油分离装置的重要组成部分，其主要指标是减小脱丁烷塔塔底的C4H10体积分数，具体工艺流程如图4所示，主要包括7个输入变量和1个输出变量，具体参数见表1所列。

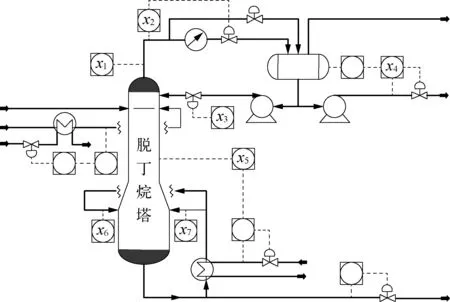
图4 脱丁烷塔工艺流程示意

x1x2x3x4x5x6x7y塔顶温度塔顶压力塔顶回流量塔顶产品流出量第六层塔板温度塔底温度1塔底温度2C4H10体积分数

对于该工业过程，C4H10体积分数无法在塔底物料流出处检测，通常通过检测塔顶的异戊烷产物间接获得。该过程产物复杂，呈现明显的非线性特性，另外化工过程的反应时间、物料传递等都加大了过程参数的滞后，无法有效地监测C4H10体积分数。因此，为了提高脱丁烷塔的控制品质，需要基于历史生产数据对C4H10体积分数进行动态软测量建模。

为了方便处理，由于输入变量x6，x7均为塔底温度，将2个变量通过计算均值简化为1个变量。对实际工业过程进行采样，得到具有2 394个样本的数据集，将所有样本平均分成2份，前1份作为训练集，后1份作为测试集，所有样本采样时间均为12 min。根据专家知识，脱丁烷塔C4H10体积分数检测仪表均存在15 min的测量周期，获得C4H10体积分数值存在30～75 min的滞后。因此，输入变量与系统输出C4H10体积分数存在45～90 min的时间滞后[25]。

5.2 结果分析

采用本文提出的基于多元模型融合和时延变量选择的动态软测量建模方法对脱丁烷塔工业数据进行软测量建模，首先针对训练集采用第3节给出的时延变量选择策略，基于联合互信息和螺旋优化对时延变量进行优化，得到时延变量的最佳个数。然后采用第4节给出的多元模型融合策略，进行建模预测。为了突出本文方法的优越性，分别引入偏最小二乘法(PLS)和最小二乘支持向量回归机(LSSVM)对原始数据进行软测量建模。为了评价预测结果，分别计算三种方法预测的均方根误差和最大绝对误差，软测量建模得到的塔底C4H10预测体积分数与真实体积分数的预测误差曲线如图5～图10所示，软测量具体优化结果见表2所列。

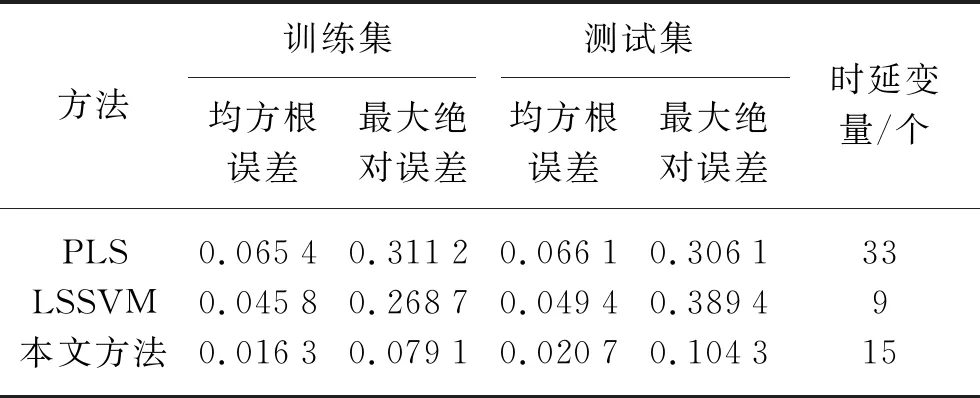
表2 软测量误差统计

通过对比表2和图5～图10可以发现，本文方法得到的软测量预测结果，无论是误差均方根值还是误差最大绝对值，均比其他两种方法要小，说明本文提出的方法具有较高的预测精度和泛化能力。由于本文通过最大联合互信息采用螺旋优化选取最佳的时延变量个数，能够充分发掘对预测有利的变量数据，剔除不利因素，且能在保证反映系统信息的情况下最大限度地减少变量个数。另外，多元模型融合策略的引入，充分利用高斯模型统计评价的特性和RELM更新速度快的优点，通过无迹卡尔曼滤波进行融合预测，动态的更新输出权重，能够充分地描述系统信息，增强预测精度和模型泛化能力，充分保证了软测量建模的性能。

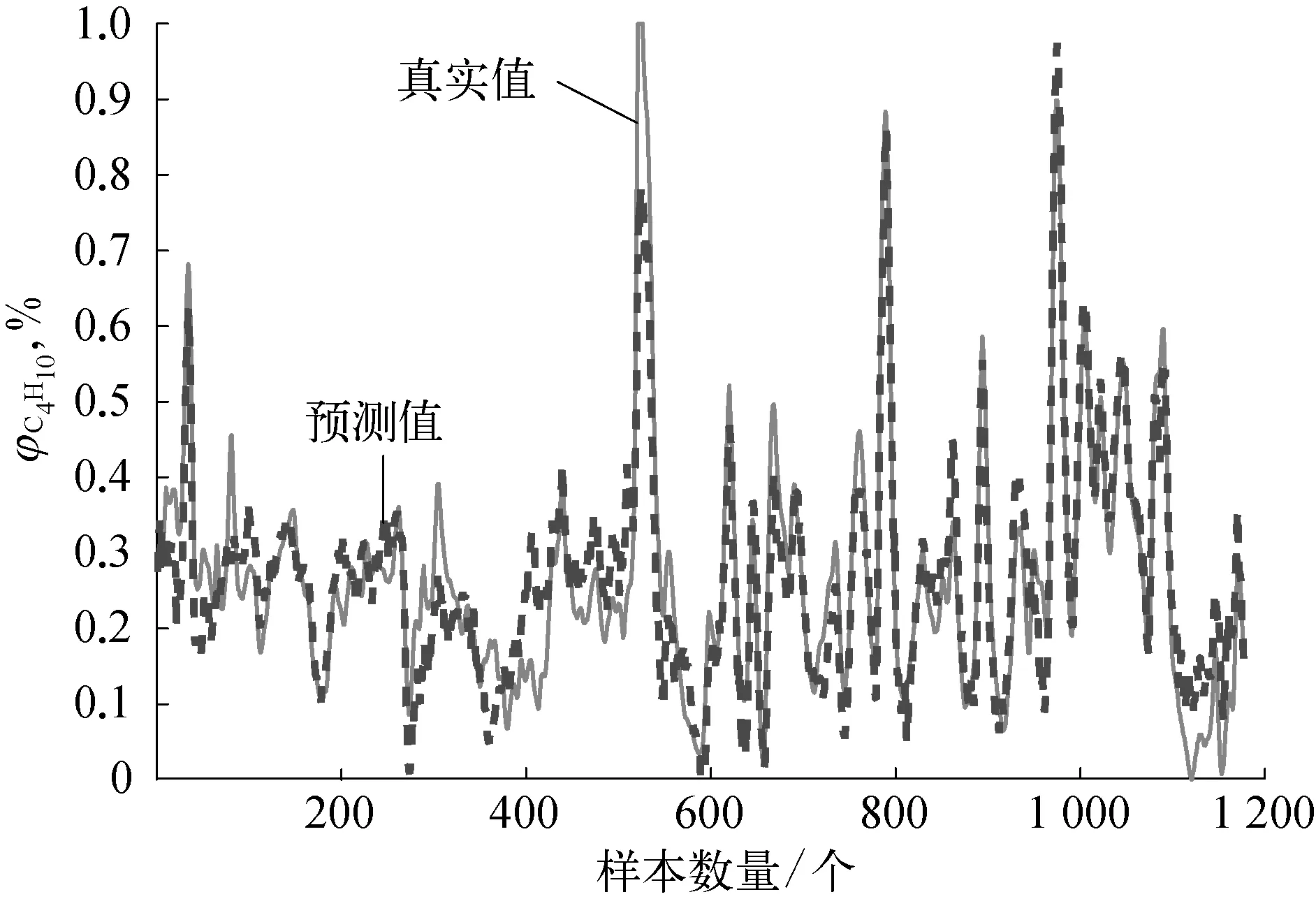
图5 PLS软测量输出对比

图6 PLS软测量误差

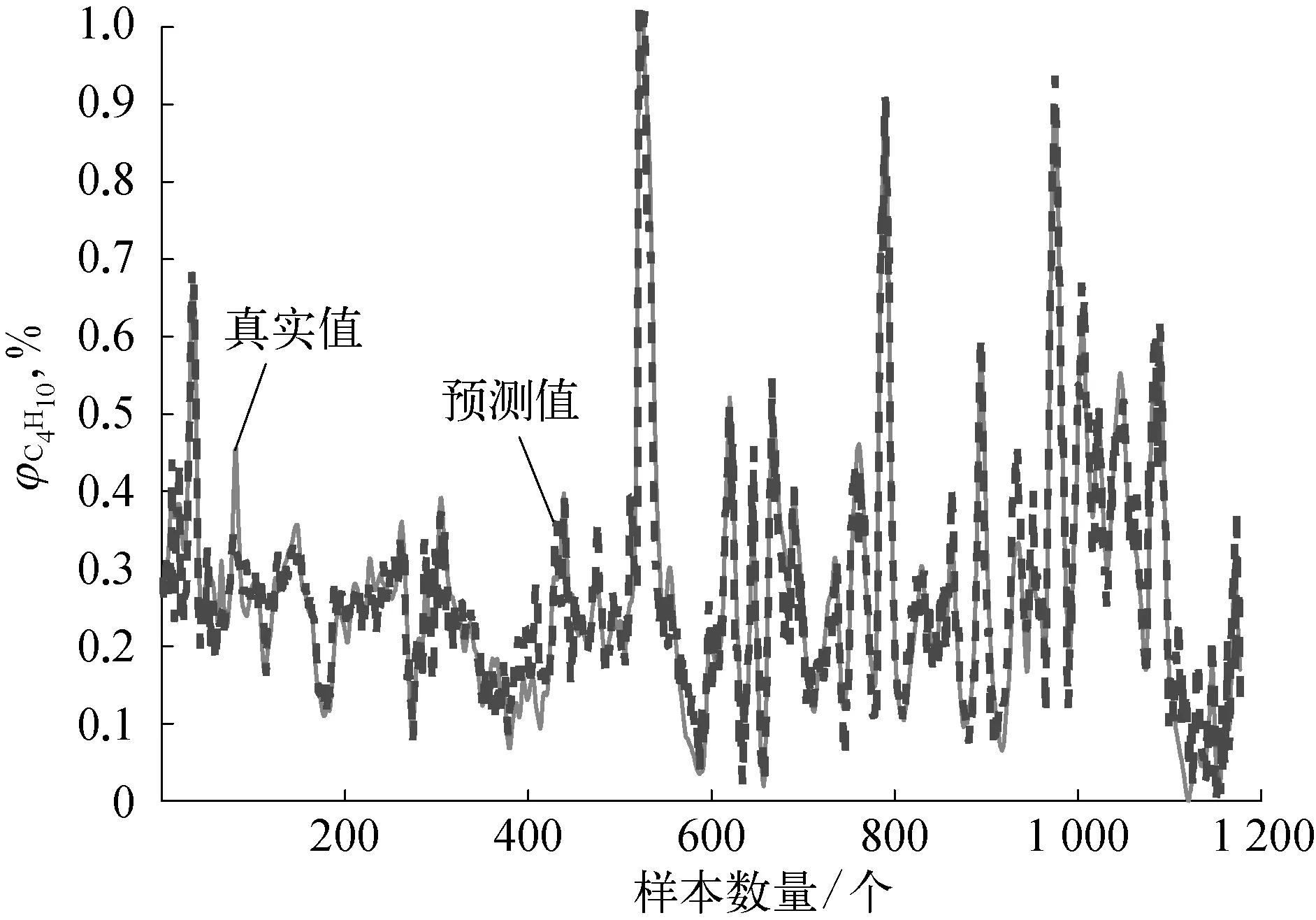
图7 LSSVM软测量输出对比

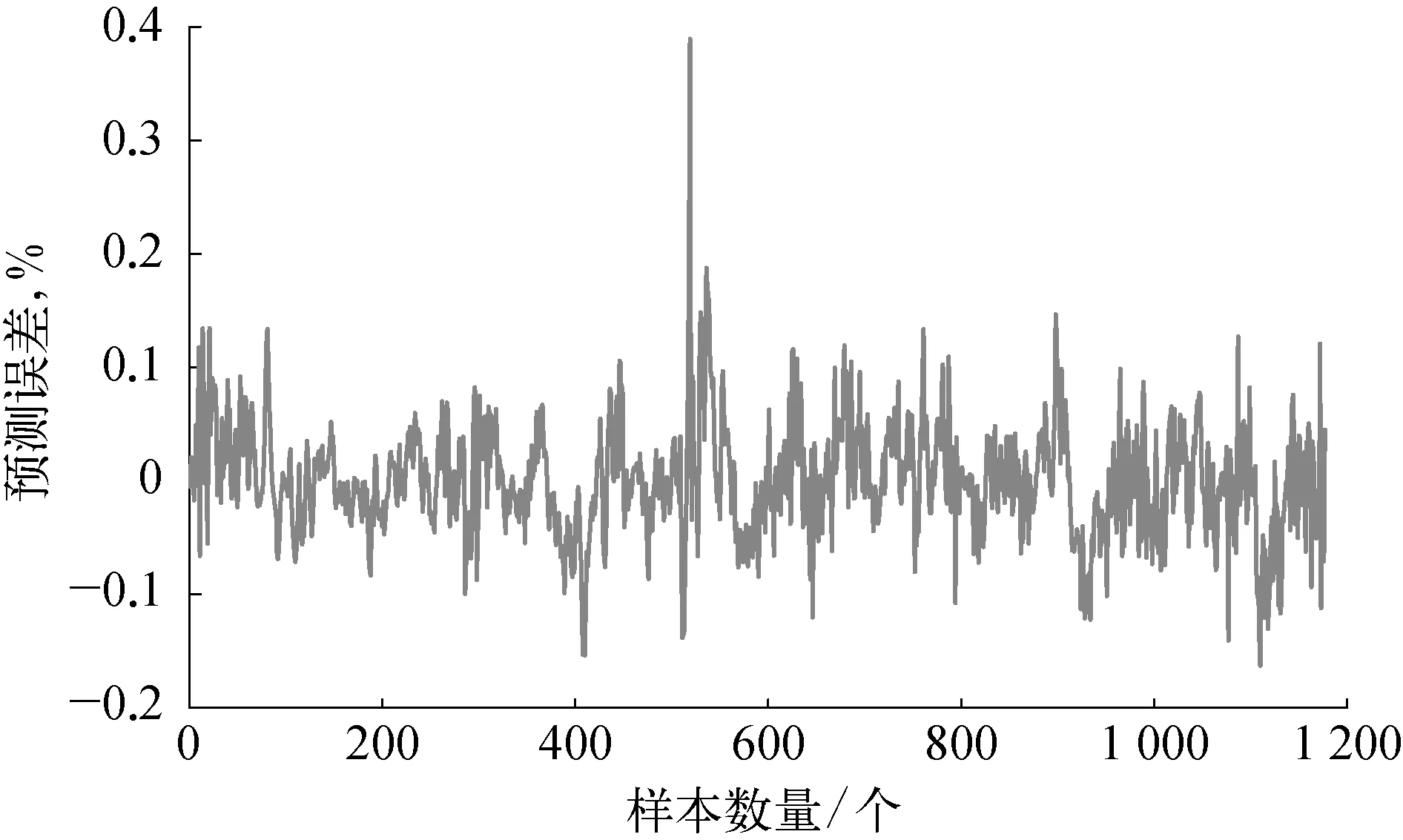
图8 LSSVM软测量误差

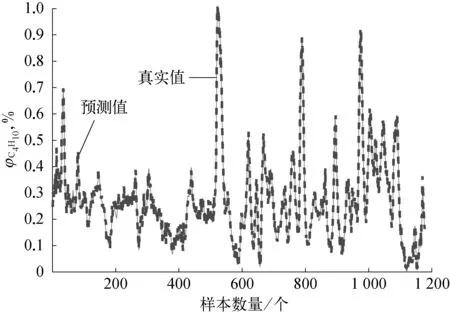
图9 本文方法软测量输出对比

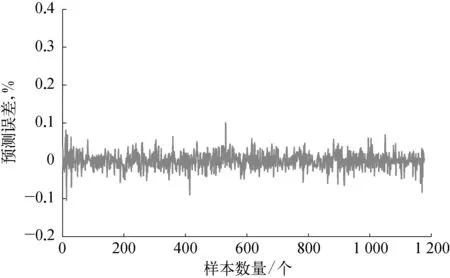
图10 本文方法软测量误差

综上可知，本文提出的基于多元模型融合和时延变量选择的动态软测量建模方法，具有很好的建模精度和泛化能力，能够有效地解决复杂非线性、带时延的工业过程动态软测量建模问题。

6 结束语

本文提出了一种基于多元模型融合和时延变量选择的动态软测量方法，能有效地解决工业过程中难以测量参数的软测量问题，方法的主要结论如下：

1)引入联合互信息评价指标，通过螺旋优化对时延变量参数进行寻优，最大程度上反映了系统信息，减小了变量个数。

2)引入多元模型融合策略，充分发挥了高斯模型和RELM在建模方面的优势，将统计评价和最小范数求解相融合，通过无迹卡尔曼滤波进行参数更新，动态更新软测量模型，提高了模型精度和泛化能力。

3)本文的软测量建模方法对脱丁烷塔底C4H10体积分数的软测量取得了很好效果，但是所提方法不仅适用于带时延的工业过程，对于科研和生活中常见的建模问题，也具有较好的建模精度。

4)本文仅考虑了多入单出系统的软测量建模，对于多入多出系统，本文方法同样适用，不过计算复杂度会增加，后续研究可以从多入多出系统建模效率展开。