环向缠绕气瓶金属内胆表面裂纹的应力强度因子计算
王汉奎 徐 彤 翟建明 桂乐乐
(中国特种设备检测研究院 北京 100029)
气瓶是一种用于存放气体,可反复充装的压力容器,广泛用于气体运输。传统气瓶为I型气瓶,多由高强钢制成,I型气瓶自身重量大,气体运输效率低,为提高气体运输效率,以复合材料取代部分钢材研制出II型气瓶[1]。II型气瓶是在金属内胆上环向缠绕纤维而成,复合材料为金属分担一部分压力载荷,从而减少金属壳的厚度,达到减重的目的。
应力强度因子是气瓶安全评估及寿命计算中的一个重要参量。疲劳破坏是复合材料气瓶的一种重要的破坏形式,其金属内胆在反复充装的作用下,所承受的应力周期性的变化,疲劳裂纹会在金属内胆表面萌生、扩展,裂纹扩展行为可用Paris公式进行描述;外层复合材料整体抗疲劳性能优异,整个疲劳周期内刚度衰减小[2]。金属内胆的疲劳寿命决定整支气瓶的疲劳寿命,若疲劳裂纹扩展贯穿金属内胆后,气瓶由于密封性的丧失而失效。因此II气瓶寿命可用Paris公式估算,需要计算应力强度因子。
II型气瓶生产过程需要经历自紧。自紧工艺是高内压使金属内胆产生永久塑性变形,以改善金属内胆和复合材料的应力分布。自紧压力是II型气瓶生产的一个极为重要的工艺参数[3],直接影响金属内胆与复合材料的应力分配进而影响内胆的应力强度因子。
目前研究主要集中复合材料气瓶整体的应力分析、寿命计算等方面,已有自紧压力与整体应力分布和寿命关系研究文献[4],主要研究方法是采用有限元模拟。如柴森研究了气瓶纤维应力比[5],王小燕研究缠绕气瓶承载能力[6],王静娴研究整体疲劳寿命[7],对气瓶损伤的研究主要集中在复合材料[8],由宏新研究复合材料层表面缺陷的安全性评价方法[9]。但对复合材料气瓶内胆应力强度因子研究较少,Chen利用Abaqus计算了不考虑自紧作用,内胆应力强度因子并进行讨论[10]。本文利用弹塑性力学理论,推导得出气瓶在不同工况下的应力表达式,结合平板表面裂纹的应力强度因子的计算公式,给出考虑自紧作用,金属内胆表面裂纹的应力因子理论解。
1 理论分析
1.1 平衡关系
复合材料气瓶如图 1所示,是由内、外两层构成的旋转壳结构,内层为金属,外层为复合材料。气瓶半径R,金属内胆厚ts,外层复合材料厚tc,气瓶受内压p。因为气瓶壁厚远小于半径R,气瓶可简化为薄壁结构进行力学分析,仅考虑膜应力作用,受力如图2所示。复合材料轴向应力为σZC,周向应力为σθC;内胆轴向应力为σZS,周向应力为σθS。气瓶承受内压P时,两种材料的应力满足轴向与周向的平衡关系,见式(1):
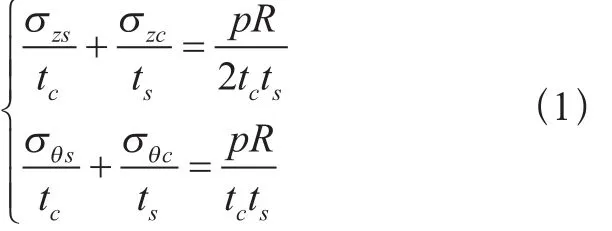
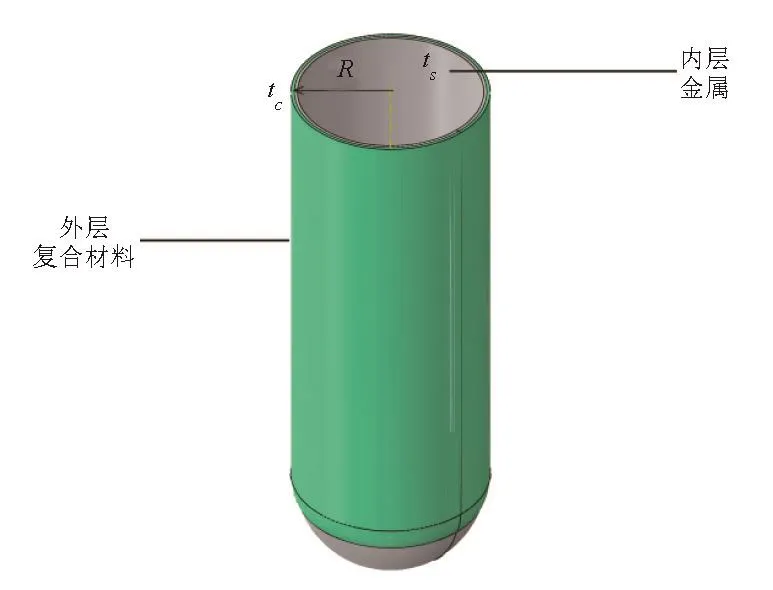
图 1 II型气瓶示意图
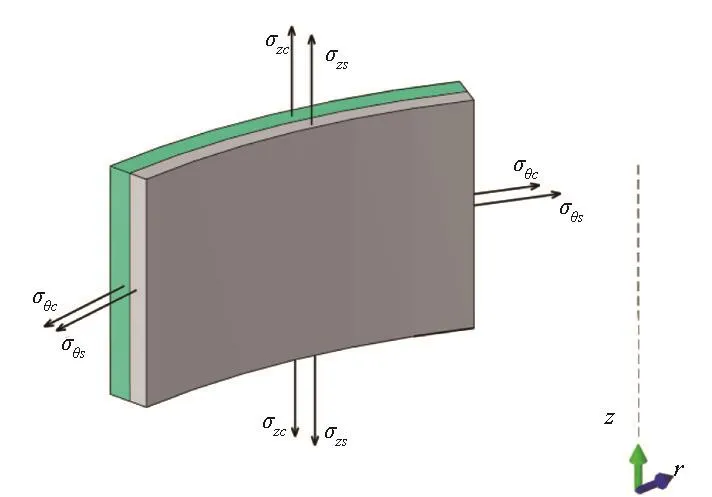
图 2 气瓶壳元示意图
1.2 本构关系
为了解两种材料的力学行为,选取II型气瓶常用材料进行测试,内胆材料为4130X钢,外层材料为E玻璃纤维复合材料。金属内胆依照GB/T 228.1《金属材料拉伸试验第1部分室温试验方法》标准[11],制成标准棒状拉伸试样并进行试验;外层复合材料依据GB/T 1447—2005《纤维增强塑料拉伸性能试验方法》标准[12],制成板状拉伸试样并进行测试,两种材料的拉伸试样图 3所示,拉伸试验所得两种材料的应力关系如图 4所示。

图 3 4130X钢和复合材料拉抻试样
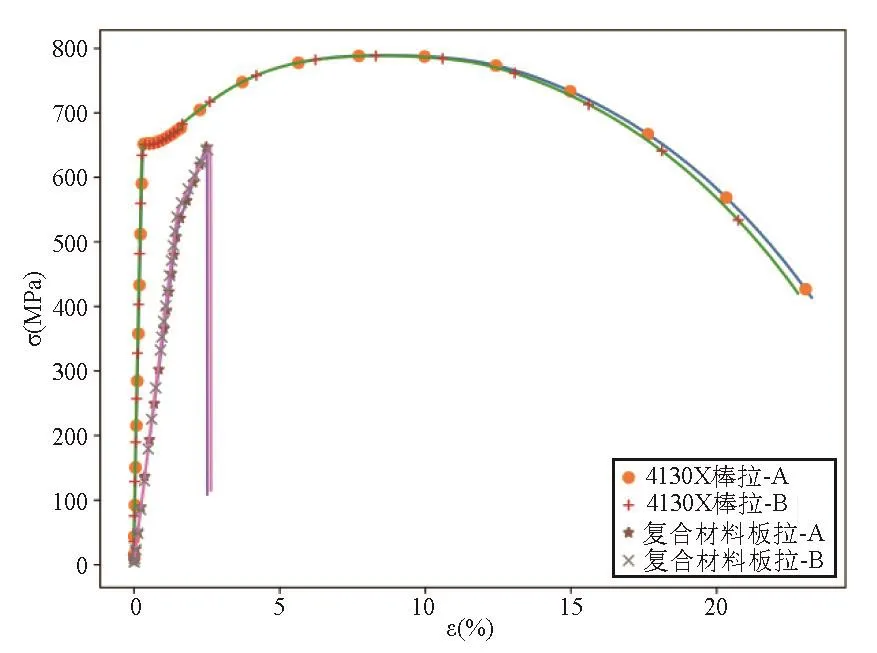
图 4 4130X钢和复合材料试验所得应力应变关系
考虑到气瓶自紧过程及之后服役过程的最大应变约为0.01,截取应变小于0.015部分的应力应变关系并放大如图5所示。在应变小于0.015的范围内,4130X为弹塑性变形,复合材料为弹性变形。为便于理论推导,内胆材料用理想弹塑性模型,如图6所示,杨氏模量为Es,屈服强度为Y,外层复合材料用理想弹性模,沿气瓶周向杨氏模量为E11。
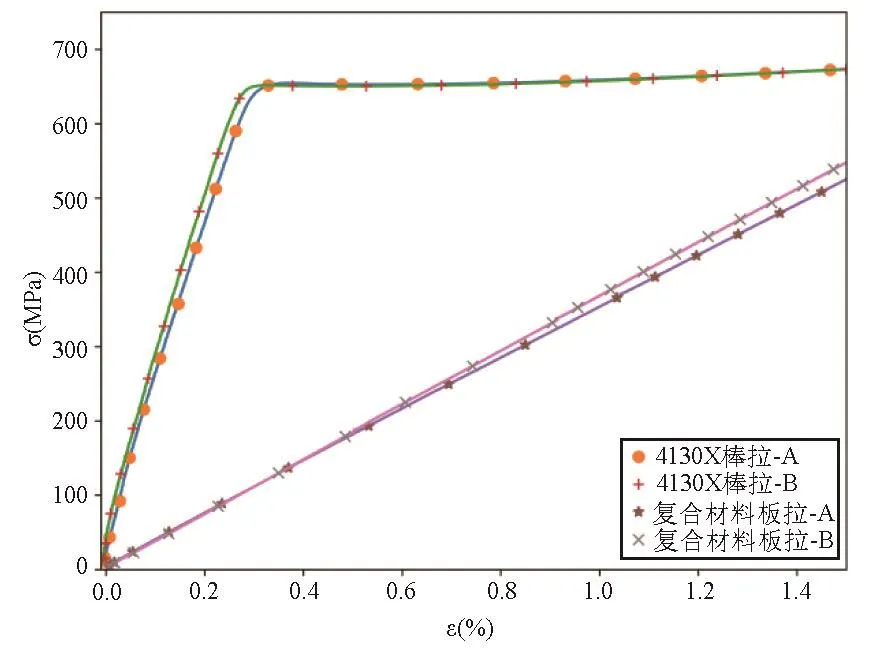
图 5 4130X钢和复合材料应力应变关系(局部ε<0.015 )
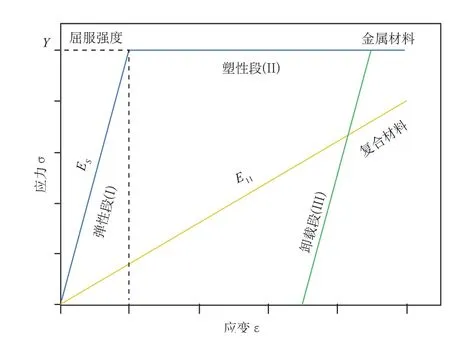
图 6 4130X钢和复合材料的力学模型
1.3 变形过程理论解
气瓶在缠绕完成后,自紧之后投入使用,整个过程的压力曲线如图7所示。当自紧开始时,金属初始变形为理想弹性材料,处于弹性段(I),当内压增至p=pY,内胆开始屈服;内压进一步增大p>pY,内胆进入塑性段(II),变形迅速增加,直至达到自紧压力pa;自紧完成后泄压,内胆沿卸载段(III)变形。气瓶服役时,受压力为pw的循环载荷,因pw<pa,股役过程中,内胆应力应变沿卸载段(III)变形。外层复合材料在整个自紧、服役过程中,均保持弹性变形。
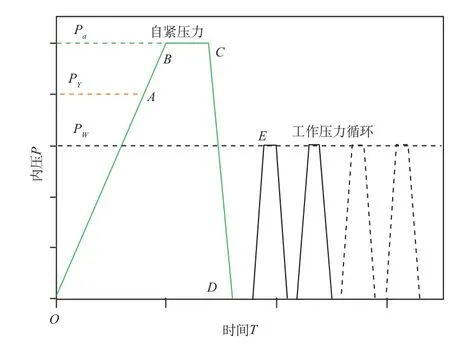
图 7 气瓶经历的压力曲线
复合材料为正交各向异性材料,其应力应变关系可由式(2)进行描述[13]。
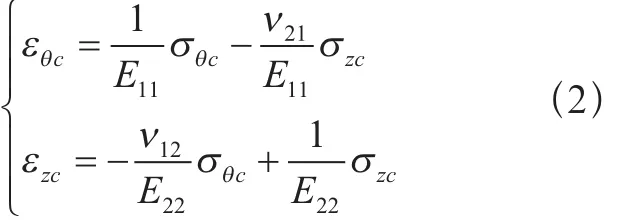
式中:
E11——气瓶周向弹性模量;
E22——轴向弹性模量;
ν12和ν21——泊松比,满足ν12/E22=ν21/E11;
εθC——周向应变;
σθC——周向应力;
εZC——轴向应变;
σZC——轴向应力。
内胆为理想弹塑性模型,当处于弹性段(I)时,此时金属的应力应变关系见式(3)。
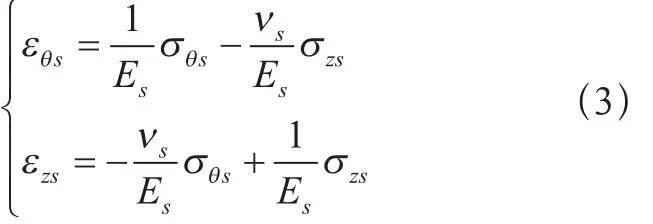
式中:
Es——杨氏模量;
νs——泊松比;
εθS——周向应变;
σθS——周向应力;
εZS——轴向应变;
σZS——轴向应力。
当内压增至p=pY,内胆材料屈服,屈服强度Y,金属的Tresca屈服判定条件见式(4)。当压力进一步增加,内胆材料应力处于屈服面上,内胆材料的塑性流动性可利用Prandtl-Reuss方程描述[14],见式(5):
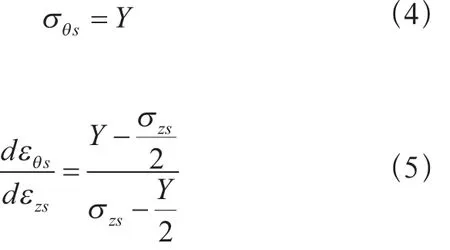
假设在自紧及之后的服役整个过程中,外层复合材料与内层金属完美结合,两者应变相等,见式(6),记为 (εθ,εZ):

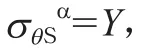
当内压到达自紧压力pa时,金属内胆的周向应力联立方程(1)-(5),求解可得pa时,内胆轴向应力满足:
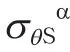
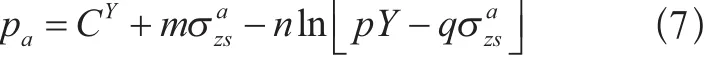
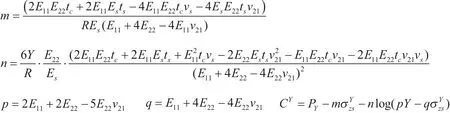
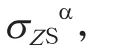
式(7)为超越方程,需要利用数值方法解得由式(1)、式(2)和式(7)可得复合材料层内应力应变
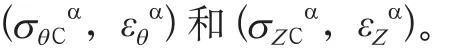
当卸载时,塑性变形保留,金属沿卸载段III变形时,应力应本关系见式(8):
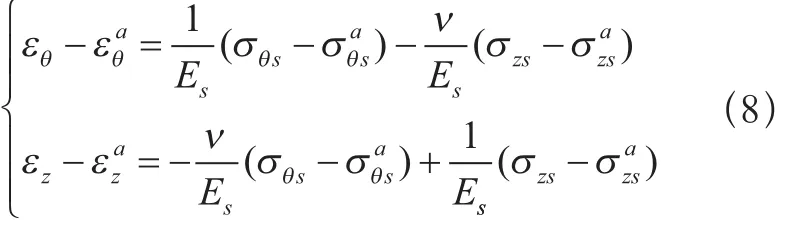
联立式(1)、式(2) 、式(6) 和式(8)求解可得经过自紧后,在压力为p时,内胆与缠绕层周向应力依次为:
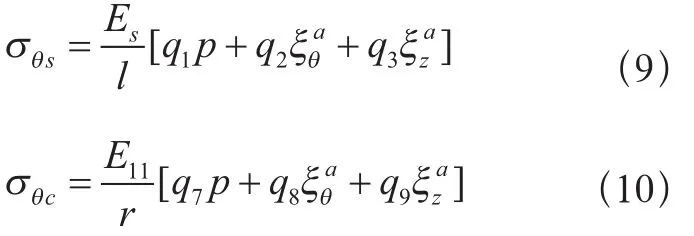
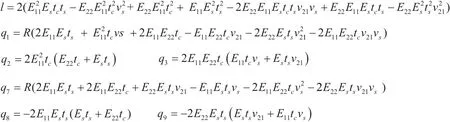
由式(9)、式(10)可见,经过自紧的气瓶在循环载荷作用下,载荷变化幅内胆应力变化幅复 合 材料层应力变化 幅气瓶周向应力变化范围仅与气瓶材料、壁厚及载荷相关,与自紧无关,气瓶轴向应力变化也满足同样规律。
为保证气瓶安全,标准要求气瓶承受工作压力pw时,内胆应力复合材料纤维应力式中α为内胆材料安全系数,取α=0.6,β为复合材料安全系数,取β=1/2.8,X为复合材料周向抗拉强度。为防止内胆屈曲失稳,气瓶在零内压下p=0,要求通常取γ=0.5,利用这些关系,可以求出满足要求的最小自紧压力和最大自紧压力利用式 (9)、式 (10)求得,当内胆与复合材料层分担气瓶压力比例为1:1时,所需要的自紧压力工程实际中常用体积变化量∆V/V衡量自紧程度,忽略封头部分体积变化,气瓶体积变化近似为
在疲劳作用下,裂纹会在内胆表面萌生、扩展,假设内表面已产生一椭圆形裂纹,裂纹长2c,深为a,利用平板表面椭圆形裂纹应力强度因子计算公式[15],内胆疲劳裂纹的应力强度因子可写为式(11):
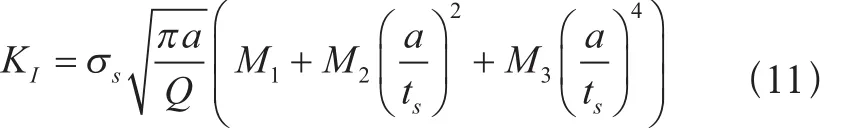
式中:

2 算例计算
以某II型气瓶设计为例,该气瓶工作压力pw=25MPa,内胆选用4130X钢,外层采用E玻璃纤维环向缠绕,内胆半径R=279.5mm,内胆壁厚ts=10.0mm,复合材料层厚度tc=12.5 mm,内胆材料参数见表1,复合材料参数见表2。利用式(11)可计算求得不同裂纹所对应的裂纹强度因子,见表3,在气瓶自紧及服役阶段,气瓶应力、应变计算结果见表4。气瓶的轴向应力与周向应力随内压的变化关系如图 8、图9所示,气瓶体积变化随压力变化曲线如图10所示,气瓶周向与轴向应变与应力间的关系如图 11、图 12所示。(图8~图12中细线段表示自紧过程,粗线段表示工作压力循环)。

表 1 4130X钢材料参数

表 2 E玻璃纤维缠绕复合材料参数
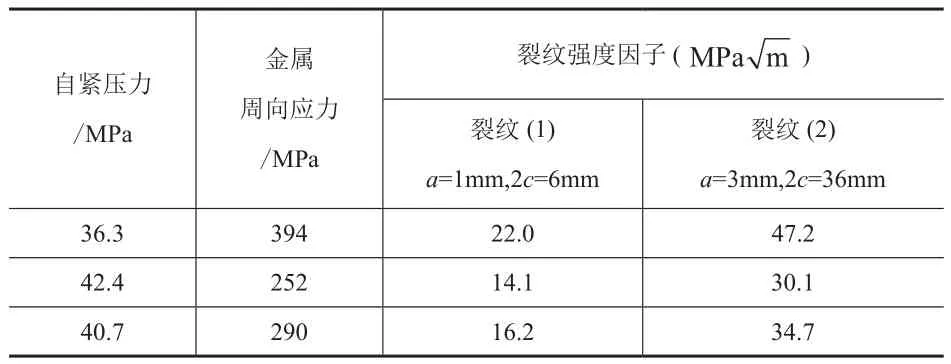
表 3 工作压力下裂纹的应力强度因子
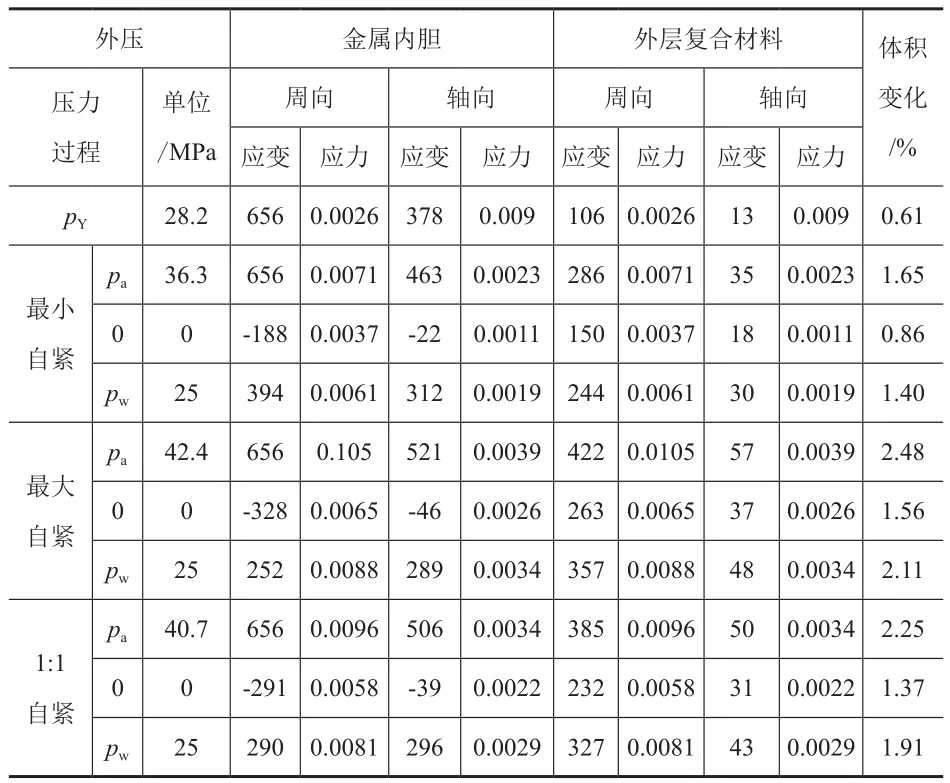
表 4 利用公式,气瓶应力应变计算结果
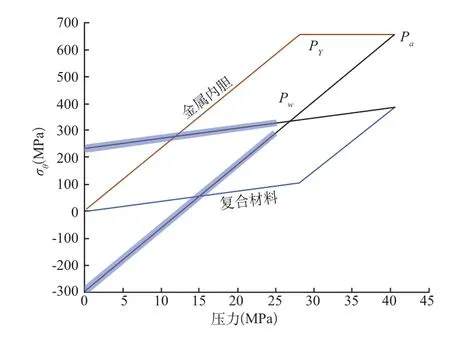
图 8 气瓶周向应力随压力变化
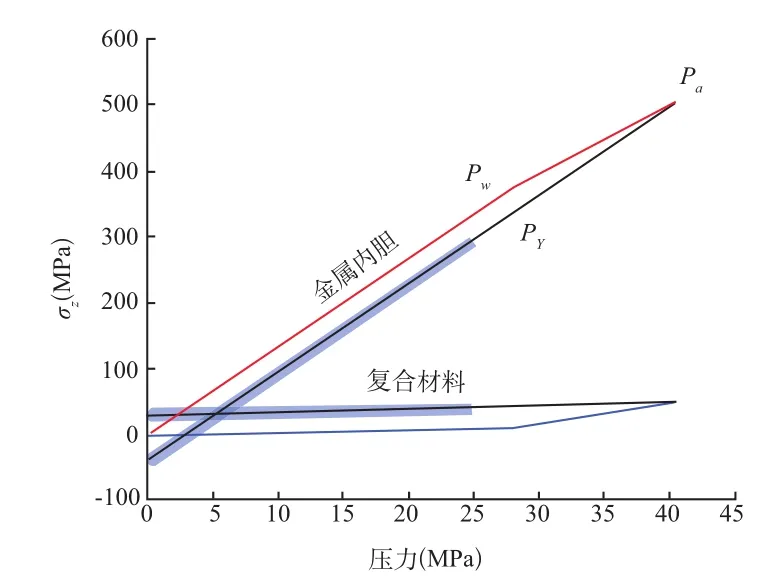
图 9 气瓶轴向应力随压力变化
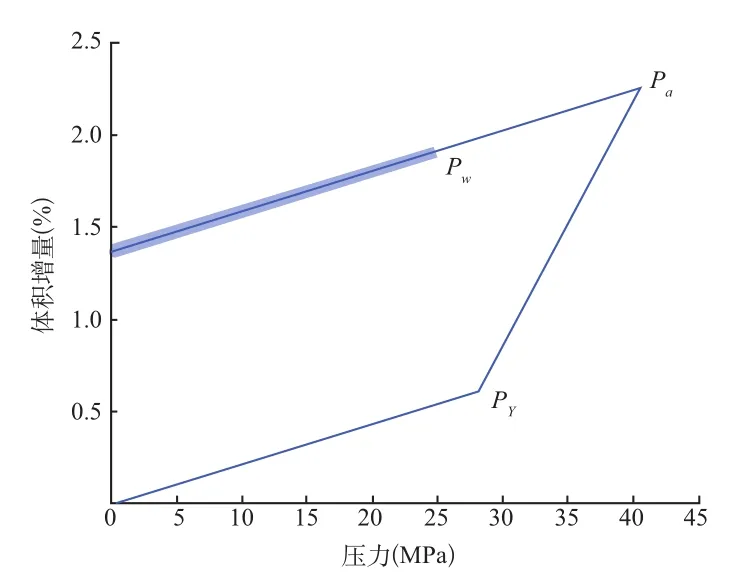
图 10 气瓶体积随压力变化
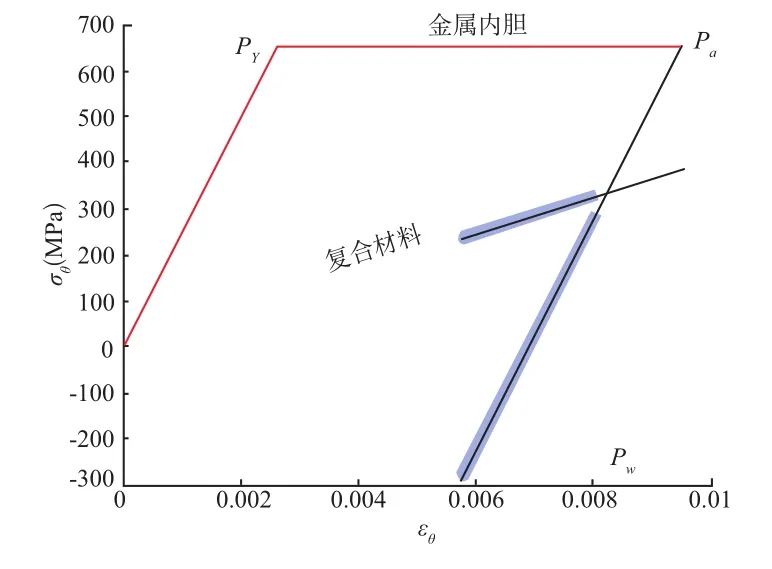
图 11 气瓶周向应力应变
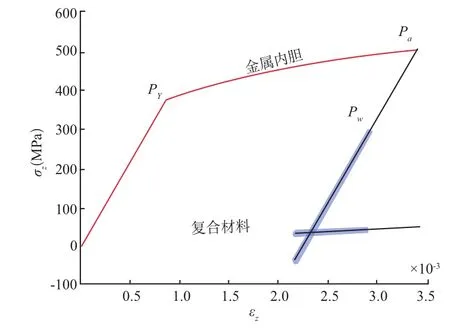
图 12 气瓶轴向应力应变
3 结论
本文对II型气瓶的受力情况进行理论分析,推导得出气瓶自紧及随后的服役过程中应力与应变的解析解,结合平板裂纹应力强度因子公式解,给出气瓶内胆表面椭圆形裂纹应力强度因子的计算公式。并针对一种常用II型气瓶设计进行计算,计算表明:
1)内胆与复合材料的应力变化幅仅与材料属性、设计壁厚和服役时压力相关,与自紧压力无关。
2)自紧压力直接影响内胆应力,气瓶制造时自紧压力越大,服役时内胆应力越小。周向应力受自紧压力影响更大,在所选算例中,自紧压力由最小36.3MPa上升至最大42.4MPa,自紧压力上升18%,气瓶周向应力下降36%,轴向应力下降7%。
3)25MPa工作压力,内胆厚10.0mm,缠绕层厚12.5mm的玻璃纤维缠绕气瓶,内胆有深1mm,长6mm的裂纹所对应的应力强度因子为深3mm,长36mm的裂纹所对应的应力强度因子为

