DEM支持下的单倾斜影像三维量测方法

熊长喜，宋碧波

(河南省基础地理信息中心，河南 郑州 450003)

倾斜航空摄影测量系统能够获取地物立面纹理信息和几何信息，为用户提供更加直观的视觉体验，已被广泛应用于数字城市与智慧城市建设中。基于人眼视觉适合观察倾斜透视像片的特点，倾斜影像测量技术更适合于网络环境应用[1]，而借助单张影像的三维量测技术能够进一步满足非专业用户定量分析的需求，对于拓展倾斜影像应用范围具有重要意义[2]。

从影像中提取真实地理信息，需要采用立体摄影测量方式将影像变换至物方坐标系，并借助专业硬件设备实现[3-5]。为克服专业设备限制，对于一些规则地面物体，可以借助其构成元素间的几何关系，在单张航片上进行三维量测。对此，许多学者根据已有空间数据(如DEM、DSM、矢量图形数据等)，基于中心投影共线方程、灭点理论、RFM、阴影长度等开展了单片量测及精度研究[6-10]。如文献[5]利用近景影像和DEM的空间位置关系迭代解算地面坐标，并证明了单像投影变换的收敛性，但该算法仅适用于地表点，无法实现高出地表的地物量测。文献[6—7]在已知影像成像高度角、太阳高度角及建筑物的顶点和对应阴影顶点在影像上的精确像素坐标的情况下，根据空间关系构建数学模型，进而计算建筑物高度，该方法受限于影像中阴影呈现效果，无法应用于建筑物密集区。文献[8]提出利用合点原理求解单张影像外方位元素，并借助已有的二维GIS信息获取建筑物平面信息，在此基础上解算比例因子，获取高度信息，但该方法需要从二维GIS信息中计算两点的距离信息，不利于广泛应用。综上所述，目前单影像三维量测方法多侧重于理论研究，缺乏实际应用，而且大多需要在专业环境下进行。因此，本文提出基于DEM数据的单倾斜影像三维量测方法，该方法利用相机检校结果及垂直影像外方位元素获取倾斜影像的内、外方位元素，对倾斜影像几何特征及影像与DEM、地面建筑物间几何关系进行分析，推算出垂直方向空间信息解算模型，并搭建测试系统对本文算法及精度进行实例验证。

1 倾斜影像几何特征分析

倾斜航摄系统能够同时获取垂直和倾斜影像，使得建筑物的侧面、地面高度变化及透视变形效果更明显，具有独特的几何特点[11]。倾斜影像的地面分辨率(行向和列向水平分辨率)、垂直面分辨率(列向垂直分辨率)具有渐变且不同的特点[12]，每个像元对应的地面范围、形状各异。在理想倾斜摄影情况下，一张矩形成像面与地面上的等腰梯形区域相对应，如图1所示。

(1)

2 本文方法

本文方法是在对倾斜影像特征进行分析的基础上，通过相机平台检校、影像畸变差修正以求解外方位元素，并对地物成像姿态进行多角度分析，推算出单张倾斜影像中水平、垂直方向上三维量测模型。

2.1 地表量测

已知影像内外方位元素即可确定像点投影光线的空间方位，其与DEM的交点即为相应物点，由此可得真实地面坐标。由共线方程模型可知，仅根据像点坐标(x，y)及内外方位元素，无法求解(X，Y，Z)3个未知数，需要通过设置初始高程与适宜步长进行迭代计算，在DEM中内插才能得到地面点位坐标。具体技术流程如图3和图4所示。

2.2 垂直方向量测方法

倾斜影像中涵盖了大量地物的侧面信息，从单张倾斜影像中提取的垂直地物立面信息可分解为垂直方向上的高度与某高度上的点位坐标。根据成像位置、姿态与地物之间的空间关系构建严密的几何模型，并推导量测算法。

位于基本方向线(主垂面与地平面交线)上的垂直地物，其像落在影像主纵线上，根据影像倾斜程度、地物位置与高度，以及量测方向的不同呈现出不同的几何关系，主要有以下7种情况(如图5、图6所示)。图中，S为摄影中心，c为焦距，t为影像倾角，N为星下点，P为像主点对应的地面点，T为垂直地物对应的地面点，dh表示实际地物的高度，dr为地物在影像中成像长度，β为摄影中心与地物点的连线与竖直方向间的夹角。以图5(a)为例，通过分析像长dr与实际高度dh间的几何关系，用已知参数表示出dh，其推导过程如下。

假设地面水平，即N、P、T这3点处于同一高度，图中S△STB=S△STA+S△ATB，借助摄影测量中特殊点、线、面间的几何关系，并利用正弦面积公式进行表示为

|ST|·|TB|·sin ∠STB=|ST|·|AT|·

sin ∠ATS+|AT|·|TB|·sin ∠ATB

(2)

式中,|ST|=h/cosβ；|TB|=dr·mT(mT为T处对应的成像比例尺)；|AT|=dh；∠ATS=β；∠ATB=90°-t；∠STB=β+∠ATB=β+90°-t。将|ST|、|TB|、|AT|、∠ATS、∠ATB、∠STB代入式(2)进行计算得到

经过进一步计算和简化，dh可近似表示为

(3)

同理，图6中S△STA=S△STB+S△TBA，按以上方法推算可得到

(4)

式中，角度β、t位于同侧时取正值，处于异侧时，则β取正值、t取负值，使得以上公式适用于图6的4种情况。

以上推算过程仅适用于基本方向线上地物的垂直量测，不具备通用性。图7为垂直高度计算中的几何关系。了图中，S为摄影中心，P、E分别为像片平面和水平地面，A′B′和AB为高度相同的两个地物，其中，A′B′位于基本方向线VV上，AB位于与基本方向线垂直的直线HH上，a′b′和ab分别为它们的像，可以看出a′b′为ab在主纵线上的投影。由于非基本方向线上的垂直地物，其空间关系无法构成上文的几何模型，因此计算地物高度时，应首先统一归算到主纵线上，再用以上关系式推算地物实际高度[13]。综上所述，利用本文算法能够实现单张倾斜影像的三维量测，对于影像中任意两点，只需首先从地面上引入其高度，即可根据像点坐标解算实地位置。

3 试验与精度分析

根据上述计算模型搭建试验平台，对单张倾斜影像的量测结果进行分析，如图8、图9所示。试验区平均高程约为90 m，最大高差小于60 m，建筑物高度从几米到几十米不等，相对航高约500 m，航向和旁向重叠分别为65%和35%，摄影比例尺约为1∶9000，DEM分辨率为0.5 m。

试验中进行了多次面向地表点和建筑物的量测，并以立体量测结果为参考开展了精度评估。在对地表点进行量测时，X坐标中误差为0.078 m，Y坐标中误差为0.125 m，Z坐标中误差为0.127 m。由于地表点位由DEM内插得到，因而地形起伏程度会对量测结果带来一定影响。在建筑物高度量测中，最大绝对误差为0.69 m，最小绝对误差为0.06 m，绝对中误差为0.45 m，由误差分布看出，不同的量测对象，真误差和中误差均存在较大差别。因此，需借助相对误差这一精度衡量指标对单片量测的精度进行补充分析，得出最大相对误差为5.40%，最小相对误差为0.39%，中误差为3.63%。对于高度为100 m的建筑物，可能量测误差为3.63 m，即每层误差约为3.63/33= 0.11 m(层高3 m)，见表1、表2。

通过对三维量测算法实现过程进行分析可知，误差主要来源于4个方面：相机检校误差、像点选取误差、DEM数据精度、计算模型中间变量近似替换带来的误差。其中，前3类误差可以通过提高相机检校精度、优化选点操作、采用高精度DEM数据等形式进行优化；第4类误差是由于对一些实际情况进行了理想化，如假设地面严格水平等，为了获得更精确的计算结果，可选取地物点T所在高度为起始面，并以此确定h值。在此基础上，模型中的角度也可根据像方或物方坐标进行求取[13-14]。

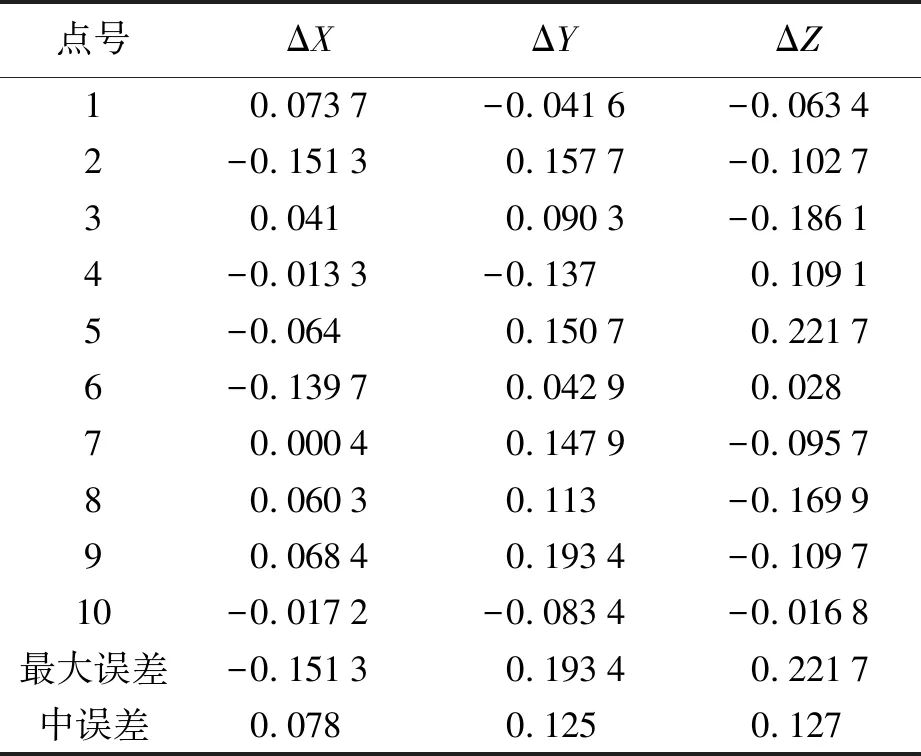
表1 地面点坐标量测误差统计 m

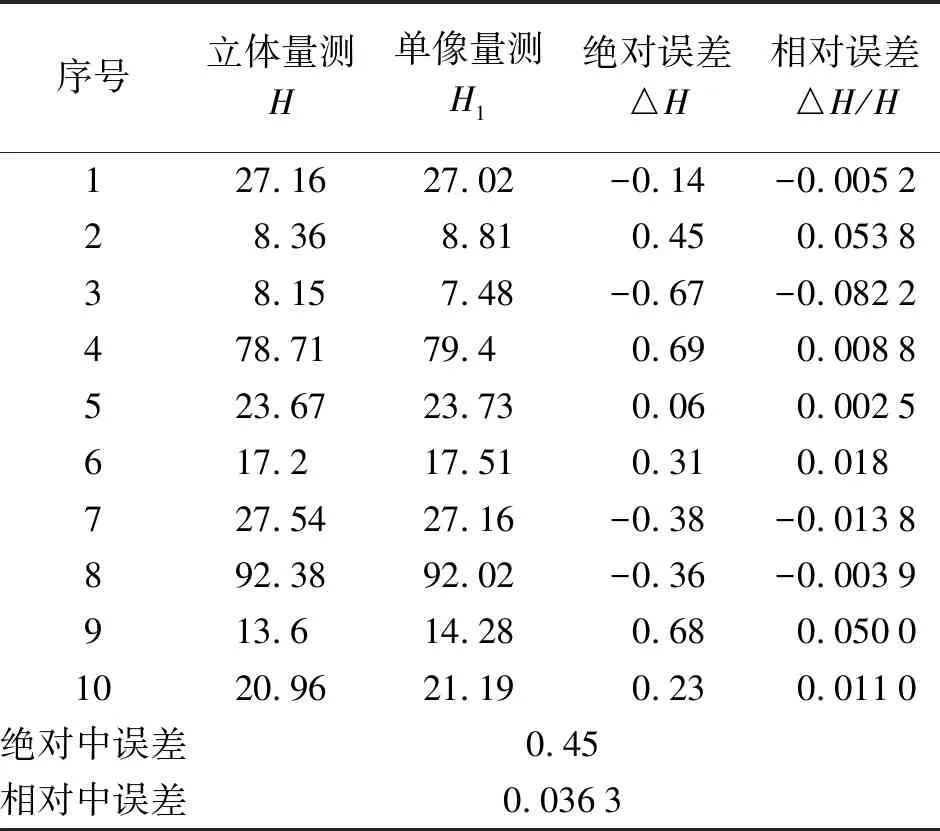
表2 地物高度量测结果 m

根据应用需求的不同，对数据精度的要求也不同，本文所构建的单倾斜影像三维量测模型主要应用于城市景观展示与规划、城市安全、房屋管理、土地利用等领域，数据精度要求较高，但又不局限于高精度的测绘数据，小于0.13 m的地表点位误差和建筑物每层0.11 m的量测误差能够满足城市管理中的量测精度要求，因此，本文提出的量测算法适用于常规测量应用。

4 结 语

基于DEM的单倾斜影像三维量测算法克服了对立体量测专业设备要求，充分利用了目前积累较多的高精度DEM 数据资源，从中提取影像对应的真实地理空间信息，既享用了倾斜影像中丰富的地物侧面信息，又满足了非专业用户的定性、定量分析需求，从而拓宽了倾斜影像的应用范围，研究结果可为城市三维数据获取提供经验和借鉴。