基于One-class SVM的大工业负荷模型研究
程婷婷 ,陈云龙 ,梁雅洁 ,张海静 ,张玉敏
(1.国网山东省电力公司电力科学研究院,山东 济南 250003;2.国网山东省电力公司,山东 济南 250001;3.电网智能化调度与控制教育部重点实验室(山东大学),山东 济南 250001)
0 引言
新能源的崛起和分布式发电技术的不断发展,打破了原有的源网荷属性,源荷界限呈现模糊化,为负荷预测增加了难度。国内外学者对新能源接入后的电网负荷建模进行了广泛的研究,提出采用神经网络、遗传算法等方法研究负荷特性[1-5],然而这些方法需要大量的样本训练模型,而且不能分行业、分用户掌握负荷变化的趋势和特性,以及负荷特性变化的原因。因此,在用户管理方面无法给电厂发电并网、电力营销、有序用电管理等提供更多数据支持。
对此,对电力市场逐级递阶分析,按照典型客户、客户群、行业负荷层级研究多时间维度 (年—季—月—周—日)多层次(全社会—行业—客户群—典型客户)负荷特性,准确反映宏观政策、生产规模对电力市场营销电价制定的影响,实现对客户用电信息的精细化研究,并分析得出导致负荷异常变化的因素。
1 大工业负荷模型建模
从典型日选取模型、相关系数选取模型、频谱分析模型、指标体系建模4个层面对大工业电力负荷模型进行分析,该模型的主要框架结构如图1所示。

图1 大工业负荷模型框架结构
1.1 典型日选取模型
采用单类支持向量机(One-class SVM)进行典型日选取,该方法通过对传统SVM进行扩展,将统计学习理论应用到无监督学习理论。
One-class SVM模型将样本集聚类,并通过改变参数,调整模型的结构风险,得到最优模型解。典型日的选择是一种聚类,假设每日的测量数据为一个样本,那么样本就是24维空间中的一个点,选择一个超球面,使其尽量覆盖所有样本点,那么超球的圆心就是测量数据的中心,即典型日数据。One-class SVM的即是用超球面来替代超平面对数据进行划分,其目标函数为

式中:R为模型半径;ξ为松弛因子,l为样本数量;c为目标变量;v为模型平衡参数0≤v≤1,通过设定参数,使超球面半径及它所包含的训练样本数目进行折中。
上述目标函数拉格朗日函数为

式中:a为拉格朗日乘积因子;β为回归参数。
对式(2)求偏导数得:

最优化方法求得优化解 ai(i=1,2,...,l)。 带入式(4)得到圆心值,即典型日。
1.2 相关系数模型
对各用户的典型日负荷曲线进行分析,可以得到用户的用电规律,以及用户与所在行业用电规律之间的关联特性。采用相关系数法可量化关联程度。相关系数表示两个随机变量的线性关系强度及方向。当两个变量之间的线性关系加强时,其相关系数趋于1或-1。当一个变量随另一变量增加而增加时,其相关系数大于0。当一个变量随另一变量增加而减少时,其相关系数小于0。当两个变量相互独立时,其相关系数是0,但反之不成立。其计算公式为

通过比较相关系数曲线,可以直观地比较各用户典型日负荷曲线之间的相似性。如果某用户A坐标上,相关系数1的附近有多条相关系数曲线聚集,将这些聚集曲线对应的用户记为集合S,则表明用户A与集合S中用户的负荷曲线相似。
1.3 频谱分析模型
用户负荷的时间序列可以看作傅里叶变换的离散采样点,对其24点数据进行离散傅里叶变换,然后分析频谱,掌握其用电波动的频率特性。
快速傅里叶变换(DFT)是一种高效、快速的离散傅里叶变换算法。采用快速傅里叶变换分析负荷频谱,可将信号变换到频域,并将信号的频谱提取出来。时域上不容易看出特征的信号,变换到频域后,能较易看出其周期特性。有限长序列x(n)的一次离散傅里叶变换运算的运算量为
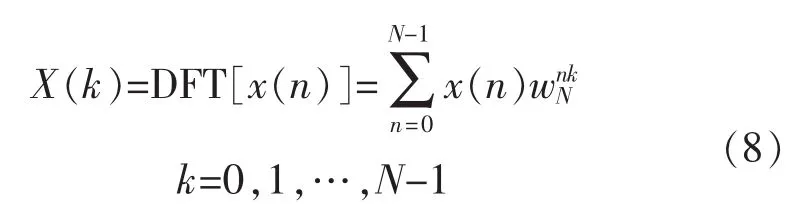
式中:w为旋转因子。
1.4 负荷特性指标体系
负荷特性分析研究中,涉及日、月、年等不同时间段的特性指标,对主要的指标进行分析。
1)月负荷率。
月负荷率是指由于用户设备检修、停工休息、新用户投入生产等引起的负荷变化情况,同时该指标也受到用户生产作业顺序不协调、设备小修等的影响。其表达式为

式中:Pdvm为月平均日用电量;Pdmm为月最大日用电量。
2)峰谷差和峰谷差率。
峰谷差是指电力系统某一周期 (一般以日为单位)最大负荷和最小负荷的差值,反映了用户负荷的波动情况。
峰谷差能够反映负荷波动的绝对值,但不能体现波动的相对值,因此用峰谷差率来反映负荷波动的相对情况。峰谷差率的计算式为:

式中:Ldmax为日最大负荷;Ldmin为日最小负荷。
峰谷差的大小体现了电网需要的调峰能力。对峰谷差的分析主要用于调峰措施、电源规划、调整负荷等研究。
3)日负荷率。
日负荷率是指日平均负荷和最大负荷的比值,即

式中:Ldav为日平均负荷;Lmax为最大负荷。
(4)日最小负荷率。
日最小负荷率是指日最小负荷和最大负荷的比值,即:

日负荷率、日最小负荷率体现了日负荷的不均衡性,负荷率越高,对电力系统的经济运行越有利。
2 大工业负荷模型分析
选取山东地区的28个大工业用户,对其负荷特性进行分析。
2.1 典型日负荷曲线分析
通过典型日选取模型获取典型日,得到各用户的典型日负荷曲线,可以对各用户日负荷曲线的相关特性进行分析。图2~3为2018年1—8月山东地区某地市28个大工业用户的典型日负荷曲线和大工业整体的典型日负荷曲线。

图2 大工业用户典型日负荷曲线

图3 大工业整体典型日负荷曲线
由大工业用户的典型日负荷曲线可以看出,在凌晨3时、11时以及17时有局部峰值出现,负荷的日内波动次数较多,但波动幅度不大。
2.2 相关性分析
求取28个用户典型日负荷曲线之间的相关系数,分析各用户负荷曲线之间的关联特性。图4为各用户与其他用户负荷曲线的相关系数。

图4 大工业各用户相关系数曲线
可以看出,19、21、22、23等用户在其序号坐标上相关系数1附近,与其他部分用户的典型日负荷曲线发生汇聚,正相关性较强。 21、22、23、28等用户与其他部分用户的典型日负荷曲线在-1附近发生汇聚,负相关较强,表明有一部分用户的用电规律与这些用户的用电规律存在较强互补性。
通过分析各用户之间的相关系数,可按其用电规律进行分类。以用户21(潍坊立特汽车零部件有限公司)为例,与其相关系数大于0.95的有用户15、16。这两个用户分别为山东金通管业有限公司、潍坊基泰铸造有限公司。这表明,与潍坊立特汽车零部件有限公司负荷特性相关系数高的用户大多是铸造相关的企业,而潍坊立特汽车零部件有限公司的主要产品也为汽车铸造配件,可以认为用户21的负荷曲线可以作为铸件生产企业的典型日负荷曲线,用户21为铸件生产企业客户群的典型用户。用户21的典型日负荷曲线绘制如图5所示。

图5 用户21典型日负荷曲线
由图5可以看出,铸件生产企业客户群日最大负荷出现在凌晨1时,最小负荷出现在13时。全天的用电规律为日间用电量小,夜间用电量大,这主要是由于该类企业由于自身能耗较高,且生产能力较为富裕。在分时电价政策的作用下,通过合理安排生产计划,利用夜间低谷电生产以达到降低企业的运行成本的目的。
2.3 频谱分析模型应用
用户15为潍坊地区某大工业用户,以此为例进行负荷特性的频谱分析。用户15负荷曲线的频谱图以及相应的功率曲线分别如图6~7所示。

图6 用户15频谱

图7 用户15功率曲线
对日负荷波动的情况进行分析,由图6可以看出,用户 15 振幅较大的频率有 30 Hz、60 Hz、90 Hz,且在频率为120 Hz、150 Hz、180 Hz处振幅也较为显著。该频率对应的为月频率,即在一个月中出现的周期性变化的次数,换算到日特性则为每天周期变化1次、2 次、3次, 相应的变化周期为 24 h,12 h,8 h。该波动规律从功率曲线中也能大致看出。
2.4 负荷特性指标体系分析
1)月负荷率。
图8为大工业各用户的月负荷率曲线。可以看出,用户24和25等多个用户月负荷率在2月份出现了明显的下降,其主要原因为该类用户在春节期间生产活动减少,使其月负荷率降低。用户1的月负荷率相对较为稳定,始终保持在0.8左右,说明该用户用电均衡性较好,月内生产计划安排的较为平均。
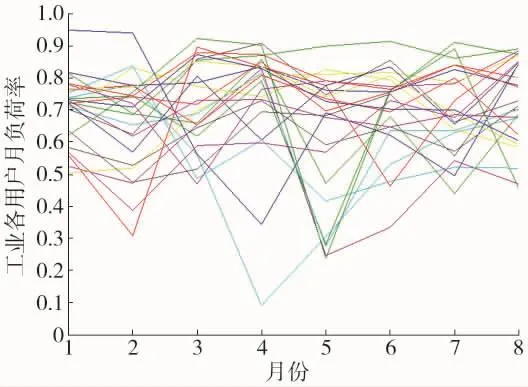
图8 大工业各用户的月负荷率
2)峰谷差。
图9为大工业整体峰谷差曲线。可以看出,该行业在上半年最小峰谷差出现在2月15日,该日为除夕,大部分大工业生产作业几乎停止,因而日内负荷波动情况较小,峰谷差较小。用户13在第146天附近峰谷差突然变大,根据其负荷曲线推断,可能是由于该段时间安排了几批较重的生产任务,而各批生产任务间留有间隙。

图9 大工业整体峰谷差
3)峰谷差率。
图10为大工业整体的峰谷差率曲线。可以看出,该行业整体的峰谷差率跨度较大,1、2月份峰谷差率较低,能够保持在0.4以下。其余各月份峰谷差波动性较强,其中最大峰谷差率可达0.75。

图10 大工业整体峰谷差率
4)日最大、最小负荷。
图11~12分别给出了大工业整体的日最大、最小负荷。

图11 大工业整体日最大负荷
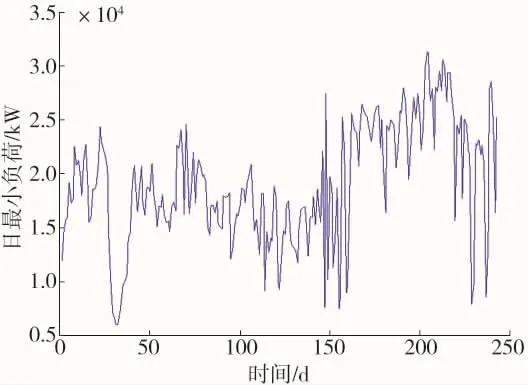
图12 大工业整体日最小负荷
可以看出,大工业的最大负荷曲线与最小负荷曲线形状较为相近,春节期间大工业的日最大最小负荷均出现明显的低谷,5月份后日最大最小负荷均有较为明显的提高,总体上看最小负荷的波动情况要大于最大负荷。
5)日负荷率、日最小负荷率。
图13~14分别给出了大工业整体的日负荷率曲线、日最小负荷率曲线。

图13 大工业整体日负荷率

图14 大工业整体日最小负荷率
可以看出,大工业整体的日负荷率保持在0.75~0.95之间,日最小负荷率保持在0.6~0.85之间。说明大工业日内用电均衡性较好。大工业的日负荷率和日最小负荷率在各月份间差异并不明显。
3 结语
从典型日选取、相关系数、频谱分析、指标体系4个层面上建立大工业负荷模型,通过对山东地区某地市2018年1月份到8月份的96点大工业负荷测量数据进行负荷特性分析,实现对大工业客户电力负荷数据的精细化研究,分析得出引起负荷异常变化的关键因素。
依照本研究模型研究山东地区全行业用户负荷特性,有效得出全行业用户负荷变化规律、特性和趋势,实现对山东地区负荷数据的实时跟踪、动态把握,为电网运行管理和电力营销服务提供了有效的数据支持。

