谐振接地系统单相接地故障暂态特性分析
陈景文, 褚恩亮, 李英春, 李 霞
(陕西科技大学 电气与控制工程学院, 陕西 西安 710021)
0 引言
在我国6~35 kV配电网系统中,为了系统的可靠性,常采用中性点不直接接地的方式,包括中性点不接地、高阻接地和经消弧线圈接地方式.其中中性点经消弧线圈接地又称为谐振接地.该电压等级的配电网系统线路结构具有多样性,使得系统故障状态下的电气量特征较为复杂.据统计,单相接地故障占到系统电气总故障的80%左右[1].该接地方式下,发生单相接地时,故障点处的故障电容电流受到消弧线圈的补偿作用,抑制故障点电弧的产生.故障相电压降至0,非故障相电压提高至3 倍,但是线电压依旧保持三相对称,允许继续运行1~2 h[2-7].因此,采用谐振接地方式可以极大提高系统可靠性,抑制电弧产生,减小故障接地电流,从而产生较小的跨步电压,保证人身安全.
但是,由于谐振接地方式下单相接地故障电流受到消弧线圈的补偿作用,其零序电流稳态量甚至比非故障线路的稳态量都小,这使得系统故障线路的判定以及故障位置的确定比较困难[8-12].目前常采用的故障选线方法均是以暂态量为主,例如首半波法、暂态无功分量法、暂态能量法等方法[13-18].但是其暂态量的提取采用对称分量法中的零序电气量作为分析对象,仅适用于理想换位下的三相对称输电线路,对于三相不对称的不换位输电线路的系统,该方法存在较大的误差[19].因此,暂态量特征的提取成为故障选线的关键.
本文通过谐振接地系统发生单相接地故障的等值电路着手,利用相模变换对三相系统进行解耦处理,提取出独立的零模分量,进而分析了故障点暂态电容电流和电感电流,以及故障全电流,并且通过PSCAD建立谐振接地系统单相接地故障仿真模型,进行定性分析.最终清晰的展示了谐振接地系统单相接地故障的暂态特性.
1 单相接地故障暂态模型建立
在理论分析中,通过简化实际传输线路模型,来进行暂态特征的定量计算.通过集总元件构建的传输线路模型如图1所示.

图1 传输线路模型结构
在图1中,r和Ll表示许多无穷小长度单元的电阻和电感,导线间和对地的电容和电导集中等效为c和g.模型中,三相电气量关系为:
(1)
正常运行时,每一相都有超前相电压90 °的电容电流,由于三相电压对称,其零序电流为0,消弧线圈不工作.发生单相接地故障时,故障相和非故障相以及故障线路和非故障线路存在不同的暂态变化过程.由于线路之间的耦合关系,使得直接分析线路电气量状态较为复杂,因此引入相模变换对三相电流解耦分析.
1.1 卡伦鲍厄相模变换
相模变换关系是由公式(2)定义的:
(2)
(3)
其相模变换矩阵中的元素均是实数,简化了相电流与模电流的转换过程.由此,可以得出模电流为
(4)
式(4)中:iA,iB,iC是相电流;i0,i1,i2是模电流分量又记为零模,1模,2模分量.依据公式(3)和(4),可以得出相电压的模分量.
1.2 单相接地故障模网络建立
根据相模变换的结果,得出谐振接地系统的模网络.以A相接地故障为例,从故障点向内部看去的各模网络为如图2所示.

图2 单相接地故障模网络示意图
在图2中,c0是零模等值电容,Ln是各模等效电感,ekn是相电压各模故障分量,ikn是相电流各模故障分量,Larc是消弧线圈,rr是故障点过渡电阻,ek(t)是虚拟的零模电压,是故障前相电压的反相电压.在动态电路分析理论中,电路条件的骤变称为换路,为了能够准确的列出暂态方程,根据故障模网络,利用电路元件的接入和切除建立单相接地故障的等值网络图,如图3所示.

图3 单相接地故障的等值网络
在图3中,r、L分别是两个线模回路的电阻、电感之和.单相接地故障的暂态过程的区别会由过渡电阻rr的不同而存在差异.
2 暂态特征量的定量计算
根据图3的等值网络,依据电路中储能元件不断交换能量的过程,可以计算出接地点的暂态电容电流和暂态电感电流,从而得出故障点的暂态电流,进而作为故障特征量.
2.1 暂态电容电流的计算
谐振接地系统发生单相接地的瞬间,故障相电压减小是的其对地电容放电,电容电压即虚拟的零模电压ek(t),有
ek(t)=Esin(ωt+φ)
(5)
式(5)中:E是幅值,ω是工频角频率,φ是故障初相角.
结合公式(5)和图3,可以列出含有暂态电容电流的回路方程
Esin(ωt+φ)
(6)
式(6)中:i0c是故障点电容电流,uc是初始电容电压.经过分析计算,化简后得出电容电流的计算方法为:
i0c=
Iccos(ωt+φ)
(7)
式(7)中:δ是暂态电容电流的衰减系数,Ic是其幅值,ωf是暂态电容电流的自由振荡角频率.
2.2 暂态电感电流的计算
消弧线圈在故障前没有电流流过,因此可以根据图3及电感的磁通列出初始条件为
(8)
式(8)中:φ消弧线圈的磁通,τL是消弧线圈回路的时间常数.根据故障回路可以得出消弧线圈的电感电流为:
(9)
2.3 暂态特征量确定
根据公式(7)和公式(9)中电流分布,电容电流和电感电流均是由两部分组成,稳态分量和暂态分量.提取二者的暂态部分最终可以得出故障点故障电流的暂态分量为:
(10)
3 暂态特征量的仿真分析
根据公式(10)可以看出,影响暂态电流的因素有故障初相角、过渡电阻和故障点距离测量点的位置.为了能够定性的比较出暂态特征,本文通过PSCAD建立了带有四条架空出线的谐振接地配电系统,其结构如图4所示.
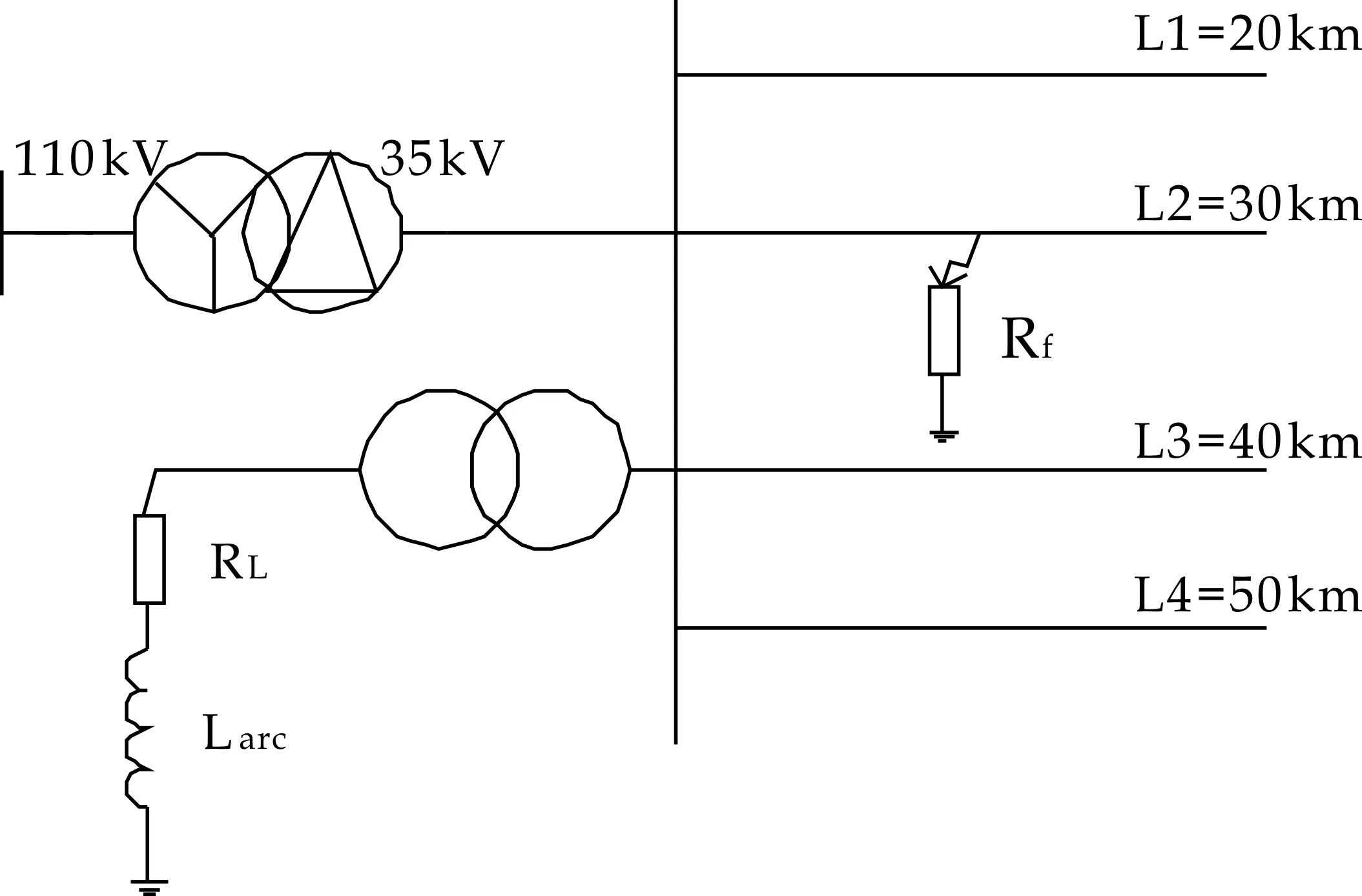
图4 谐振接地系统PSCAD模型结构
该系统是模拟某一35 kV配电系统,含有四条出线,主变采用110 kV/35 kV的Y-△型降压变压器,由于二次三角型接法,因此系统构建了Z型接地变,构造了中性点来接消弧线圈.线路长度分别是20 km、30 km、40 km和50 km,根据架空线路的标准参数,设置各线路的1模等值阻抗为:(0.17+j0.38) Ω/km,零模等值阻抗为:(0.23+j1.72) Ω/km,各线路1模等值导纳为:(j3.045)μS/km,零模等值导纳为:(j1.884)μS/km,谐振系统补偿度采用过补偿8%,并依据线路对地电容电流计算出消弧线圈电感量Larc=10.22 H,其串联电阻按照感抗值的10%计算出RL=321 Ω.
利用该系统进行不同故障状态的波形提取,首先针对故障初相角的不同进行定性分析.通过设置单相接地故障发生时所在工频周波的时刻,来改变其故障角,本文中介绍其中典型的相位,即0 °、30 °、60 °和90 °对暂态特性的影响,50 Ω、200 Ω、1 kΩ和5 kΩ对暂态特性的影响,以及故障距离不同的影响.由于架空线路的特征频带在300~1 500 Hz,根据奈奎斯特采样定理,仿真设计的采样频率为5 kHz.仿真设计线路2的A相作为接地相,然后通过计算各线路的零模暂态电流进行比较.
3.1 仿真分析故障初相角对零模暂态电流的影响
为了检测故障初相角的影响,本小节将模型中的过渡电阻设置为750 Ω,将故障距离确定为距离出线端15 km,根据线路2的A相即故障相来锁定故障初相角,仿真研究结果如图5~8所示.

图5 故障初相角为0 °时各线路特征波形

图6 故障初相角为30 °时各线路特征波形

图7 故障初相角为60 °时各线路特征波形
在图5~8中,标记处的0.820、0.836、0.854和0.870分别对应其故障角时刻.根据仿真结果可以看出,当故障初相角为0 °时,故障线路的故障零模电流高频含量占比远远小于工频分量,非故障相路直接进入稳态,其值小于故障线路稳态值;当故障初相角逐渐增大至90 °的过程中,可以看出故障线路的暂态零序电流逐渐变大,这是由于高频暂态电容电流逐渐增大.
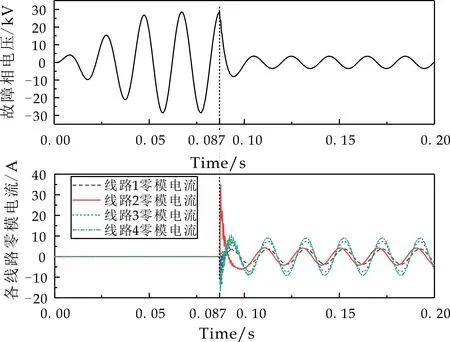
图8 故障初相角为90 °时各线路特征波形
3.2 仿真分析过渡电阻对零模暂态电流的影响
为了检测过渡电阻的影响,本小节将模型中的故障初相角设置为90 °,故障距离确定为距离出线端15 km,仿真研究结果如图9所示.
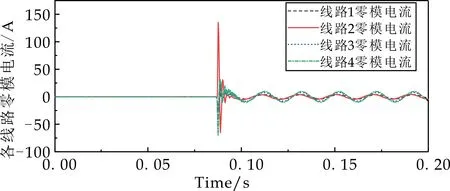
(a)过渡电阻为50 Ω
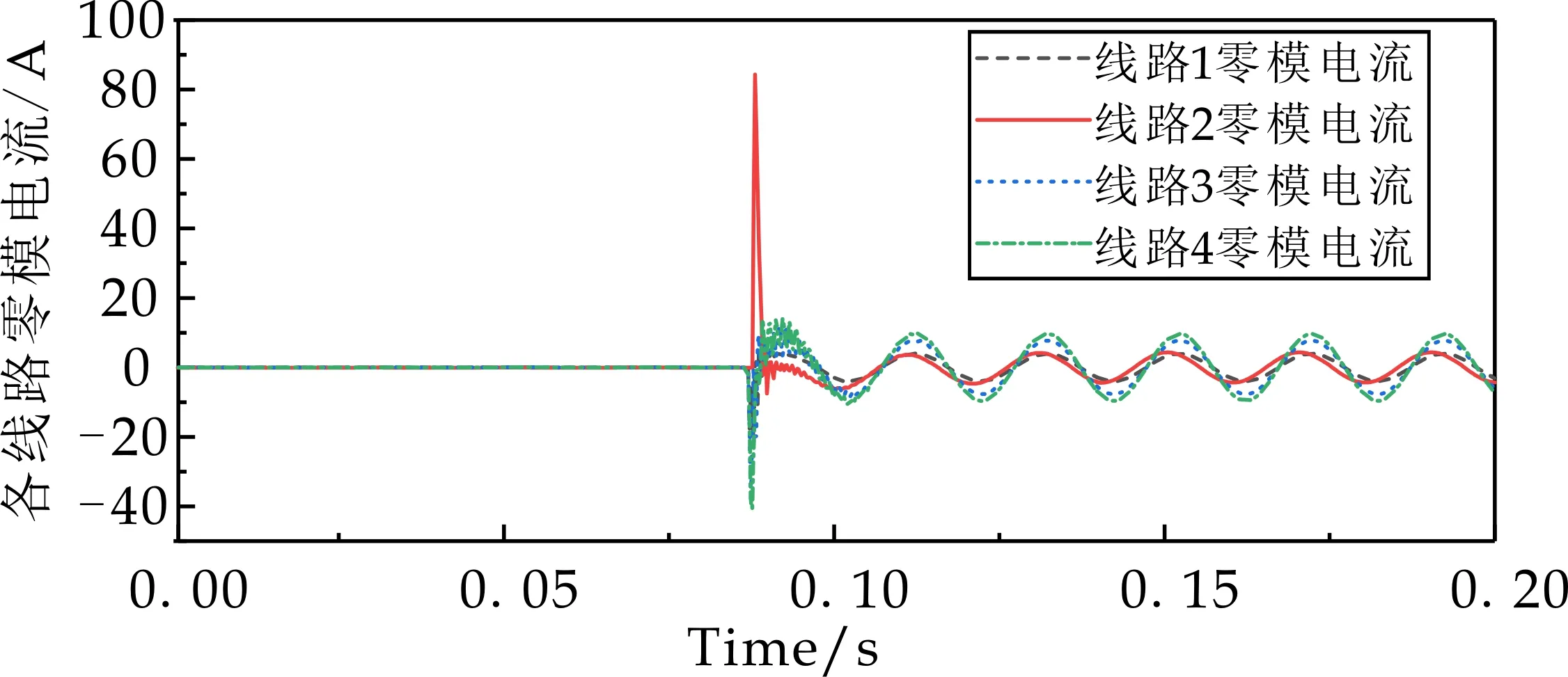
(b)过渡电阻为200 Ω

(c)过渡电阻为1 kΩ

(d)过渡电阻为5 kΩ图9 不同过渡电阻下各线路故障特征波形
通过改变故障点处过渡电阻,获取各出线的零序电流波形,可以看出过渡电阻的增大会抑制故障暂态零序电流的大小,同时缩短进入稳态所需的时间,尤其在5 kΩ状态下,系统0.01 ms内直接进入稳态.
3.3 仿真分析故障距离对零模暂态电流的影响
为了检测故障点位置距离出线端长度的影响,本小节将故障初相角设置为90 °,过渡电阻定位750 Ω,仿真试验结果如图10所示.
该线路总长30 km,从线路首端开始到线路末端发生单相接地故障,截取其故障时刻前后半周波时间段进行观察,可以看出随着故障距离的增大,暂态零模电流的自由振荡频率增大,但是影响相对较小.因此,在发生单相接地故障时,进行故障定位是一项较为困难的任务.

(a)故障点在线路首端
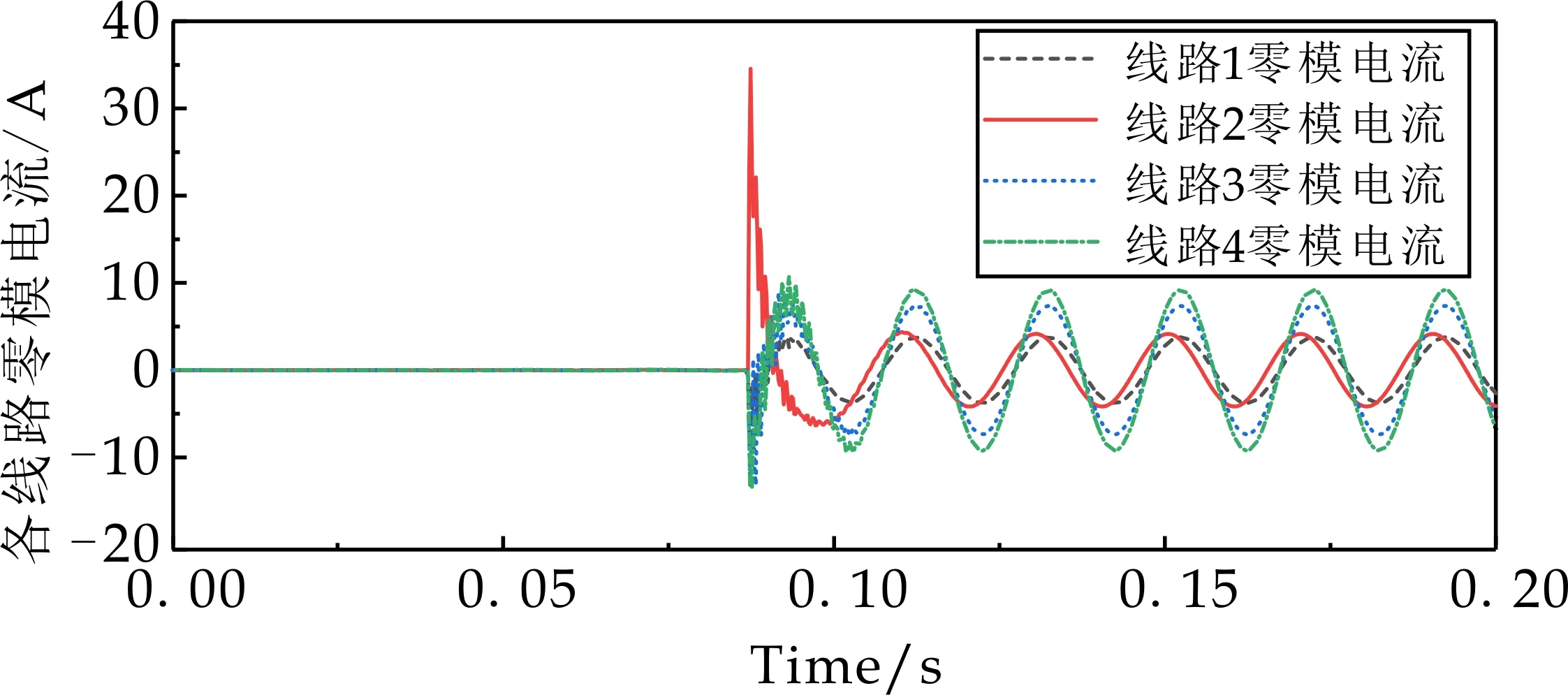
(b)故障点距离线路首端10 km

(c)故障点距离线路首端15 km
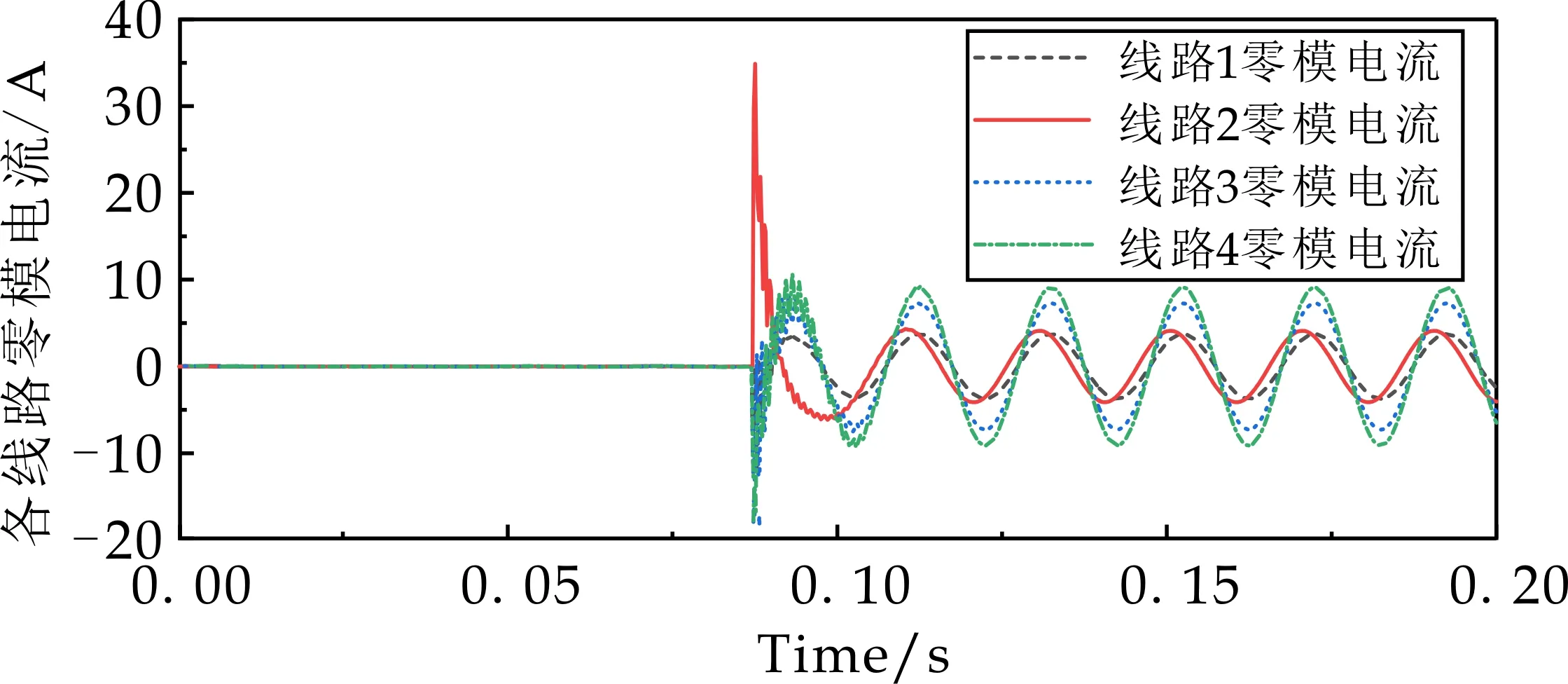
(d)故障点距离线路首端20 km

(e)故障点距离线路首端30 km图10 不同故障距离下各线路故障特征波形
4 结论
本文在谐振接地系统暂态模型的基础上,使用PSCAD对该模型进行了定性分析,比较了谐振系统的故障暂态特征.仿真研究表明,在谐振接地系统中发生单相接地故障,其故障特征主要受故障初相角和过渡电阻的影响.故障初相角直接影响故障零模电流的容性分量和感性分量的占比,从而影响故障点故障电流的大小;过渡电阻直接影响系统进入稳态所需的时间以及暂态量幅值的大小.故障位置的不同引起的故障特征不明显,因此需要使用小波分析或者其他暂态信号分析工具进行特征显式提取,这也是目前故障点定位研究比较热门的方法.
根据上述分析,故障线路的暂态零模电流与故障初相角和过渡电阻都有一定的关系,尤其是稳态量完全无法识别故障线路.本文中利用相模变换进行的暂态特征提取,为之后谐振接地系统单相接地故障的选线定位工作提供了理论依据.

