三视场星敏感器的多级星图识别算法
苟斌, 程咏梅, 赵明艳, 王会宾, 刘成元
(1.西北工业大学 自动化学院, 陕西 西安 710129; 2.盲信号处理国家级重点实验室, 四川 成都 610041)
天文导航系统利用导航星图像与导航星测量信息估计载体相对天球坐标系的姿态[1]。其中,快速、准确地识别导航星图是获取高精度姿态量测的保障[2-4]。由于恒星在天球坐标系的不均匀分布,以及载体滚转轴姿态精度与导航星间的平均分离角关系。单视场星敏感器的星图识别成功率与载体姿态解算精度都不及多视场星敏感器[5]。
传统多视场星敏感器的视场内星图识别方法需要构造导航星空间匹配特征,但多视场内的导航星分布会导致匹配特征过于复杂与庞大[6];视场间星图识别方法则利用多视场的重叠区域融合多幅星图为一副星图后再进行识别,而多视场星敏感器多采用小视场相机,视场间的重叠区域有限。对此,文献[7]提出了先视场内识别,再视场间识别的多视场星图识别策略。利用电子指南针估计星敏感器视轴指向,构建局部识别数据库缩小视场间导航星匹配范围。但电子指南针的低精度、三角形星图算法抗星点质心定位误差效果差、视场间星图匹配复杂等因素均对算法识别率和识别时间带来影响。
为了提高三视场星敏感器的星图识别效率与识别正确率,本文以三个6°×6°视场的正交三视场星敏感器为研究对象,改进先视场内识别,再视场间识别的星图识别策略,提出三视场星敏感器的多级星图识别算法。针对传统识别星图方法的缺陷,将单一可调参数的广义回归神经网络(generalized regression neural network,GRNN)引入视场内导航星识别[8];利用星库中存储的星间角距检验上一步的识别结果,以正确识别的导航星估计3个视轴指向以辅助未识别与识别错误的视场完成校正;最终以正确识别的导航星信息估计飞行器姿态。
1 三视场星图多级识别算法
1.1 算法框架
模拟的三视场星敏感器采用视场正交安装方式,如图1所示。本文模拟了三视场星敏感器在天球坐标系内的1 000组随机姿态作为实验样本,利用Smithsonian Astrophysical Observatory(SAO)[9]星表中6.5星等以下的6 970颗导航星信息模拟星图。针对每组样本,统计各视场从2°×2°到12°×12°变化过程中可捕获的导航星数,结果如图2所示。
图2表明,在1 000组6°×6°三视场星图样本中,3个视场捕获少于3颗星的概率分别为0.7%,1%,及0.5%,但不存在3个视场同时捕获少于3颗导航星的情况。为此,本文提出多视场星敏感器多级星图识别算法:第一阶段利用单一可调参数的GRNN算法进行视场内星图识别;第二阶段以星库中存储的星间角距信息检验导航星识别结果,仅当3个视场均被正确识别时进行飞行器姿态估计,否则利用已正确识别的导航星估计星敏感器3个视轴指向;第三阶段利用视轴指向辅助未识别与识别错误的导航星完成视场间识别与校正。
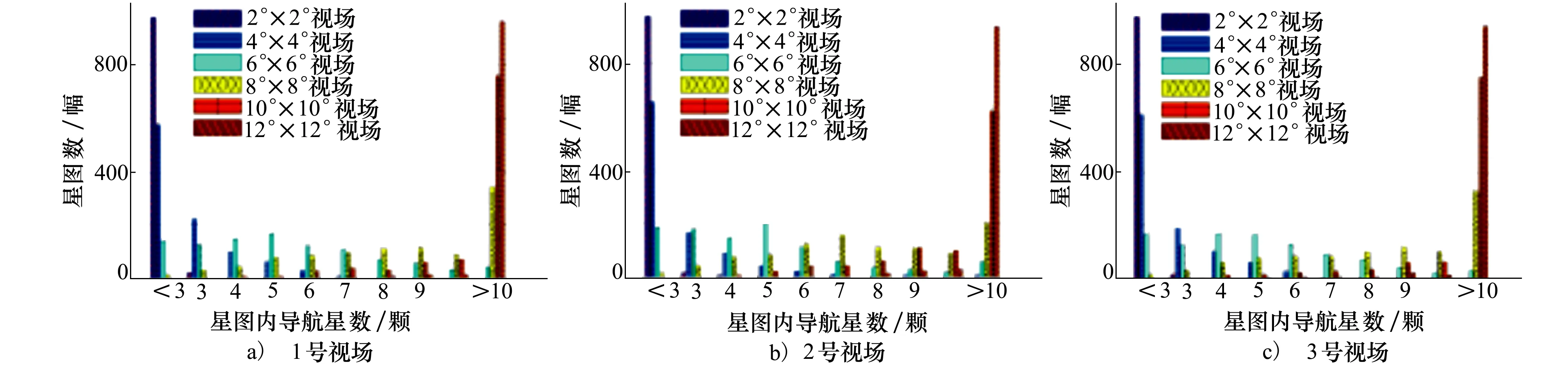
图2 视场变化下的导航星数统计
1.2 视场内星图识别
1) 特征向量建立
为了提高导航星识别正确率,提升星图识别效率,本文构建了以P值向量为识别特征的神经网络类星图识别算法[10]。单一网络输入的P值向量可以确保星图识别网络复杂度最小化[11]。
Pi=xdi-1+ydi-2+zdi-3=ΩTdi
(1)
Pi的方差D(P)越大,投影轴上的投影点离散程度最好。因此,最佳投影轴求解式为
(2)

(3)
最大特征根λ对应的特征向量即为最佳投影轴。通过对6 970颗导航星的测试得到最佳投影轴为[0.397 0.580 0.711]T。每颗导航星根据公式(1)可求出对应的P值向量,对该导航星进行编号,并将其P值与三边星角距信息一起存储在导航星库内。
2) GRNN星图识别网络
引入单一可调参数的GRNN算法进行视场内星图识别[8],在保证星图识别正确率与识别效率的同时解决传统神经网络星图识别算法过度依赖网络参数的问题。GRNN网络由输入层、隐层、输出层三部分组成。隐层的基函数常采用高斯函数对输入信号在局部产生响应。不同于传统神经网络,GRNN的调节参数只有平滑因子ρ一项。
为了确定最优ρ的选取,以上一节中3 000幅6°×6°三视场星图为实验样本。在各导航星质心定位信息中加入100组均值为0,标准差由0增至0.1像素的高斯误差;每颗导航星以计算的100组P值向量特征作为网络输入,以13位二进制星号作为网络输出;其次,ρ以0.001为步长,由0.001增至0.03,并用留P法(leave-p-out,LPO)对网络进行训练与测试,统计识别率e;最终,确定最大识别率平均值对应的ρ为GRNN星图识别网络的平滑因子。
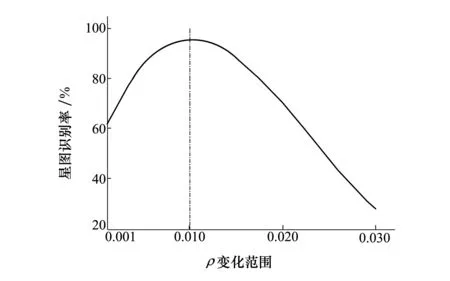
图3 导航星识别率与ρ的关系
图3表明,ρ过小会放大样本间的差异,容易使含有不同噪声的同一样本被误识别为不同样本;ρ过大会增加不同样本被误识别为同一种样本的概率。根据统计结果,本文选取最优平滑因子ρ=0.01。
1.3 视场间星图识别与校正
为了进一步提高识别正确率,首先对视场内星图识别结果进行检测。计算图中已识别导航星与其最近星、次近星间三边星角距,并与导航星库中记录的标准三边星角距进行比对。角距门限η满足下式
ϑ
(4)
式中,δ为星点的扩散半径,ϑ为单像素空间张角。
再利用上一节中已正确识别的单视场星点信息及星敏感器安装矩阵估计3个视场的视轴指向
(5)

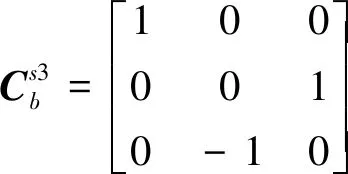
(6)
视轴指向误差范围最大值ξ由星敏感器的姿态估计误差φe决定。根据欧拉位移定理[12],当星敏感器视轴方向垂直于误差欧拉轴时,姿态估计误差对视轴指向误差范围的贡献最大
(7)
式中,tr(Re)为姿态误差旋转矩阵Re的迹。单视场星敏感器解算的姿态中滚转轴的精度远低于其余两轴,本文主要考虑滚转误差旋转矩阵对星敏感器的姿态估计误差的影响,即
(8)
根据2.1节中1 000组6°×6°三视场样本(3 000幅单视场星图)解算的滚转姿态均方根误差的统计结果。当星点质心添加了标准差为0.07像素的位置误差。滚转姿态误差θ为0.998°(1σ),最大视轴指向误差范围为ξ=φe=3°。
二次候选导航星确定条件如下
(9)
式中,RFOV为视场半径;ustar为候选导航星方向矢量,与导航星的天文信息赤经(right ascension,Ra)及赤纬(declination,Dec)有关
(10)
根据公式(9)确定符合条件的候选导航星,计算各候选导航星间在天球坐标系下的空间星角距,并与各未识别导航星与已识别导航星在载体系下星角距逐一对比;将满足星角距门限的候选导航星号作为未识别导航星的识别结果。
2 仿真与分析
实验仿真环境为Intel Core i5-6400 2.7GHz PC机;三视场星敏感器仿真视场为6°×6°,CCD面阵像素分辨率为512×512,像素尺寸8 μm×8 μm,焦距为39.078 mm;星敏感器拍摄的星图是通过Matlab2016a软件根据SAO星表中星等小于6.5的6 970颗恒星模拟生成。
2.1 视场内星图识别结果分析
本文模拟了1 000组星敏感器在天球坐标系的随机姿态作为实验样本。样本中每幅星图的星质心定位误差由1增至0.07个像素。图4统计了本文算法、三角形匹配算法(全天球识别)[11]、P值向量算法[11]、RBF[2]以及BP[3]星图识别算法在不同导航星质心定位误差下的识别率以及平均识别时间。其中,RBF、BP神经网络的训练集与GRNN相同。
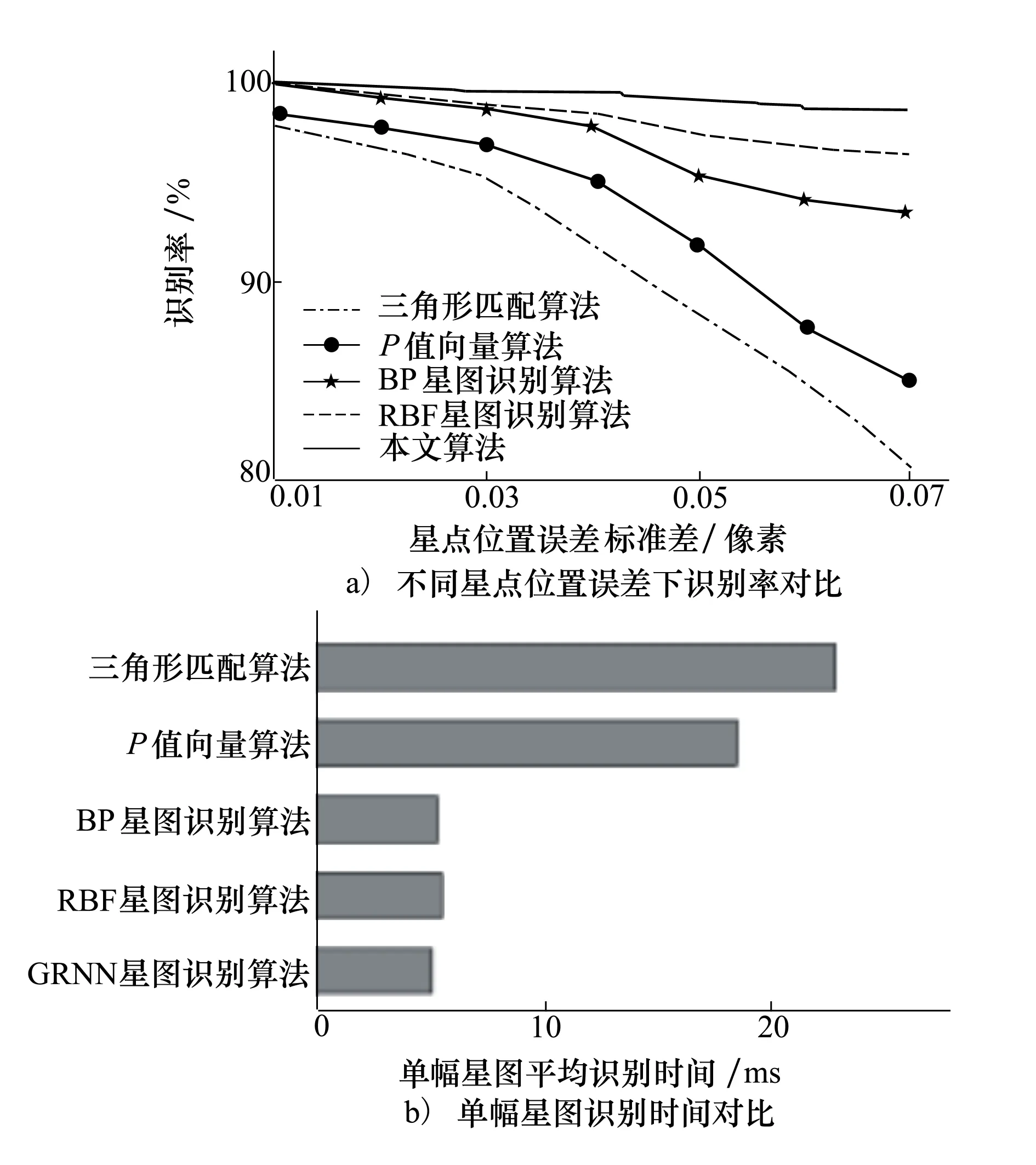
图4 各识别方法性能对比
由图4可以看出,神经网络类方法具有相似的星图识别时间,且明显优于其他方法。但本文的GRNN星图识别算法在网络训练之初就考虑了星点位置误差干扰,增加了网络的容错能力。当星点位置误差标准差为0.07像素时,本文算法在1 000组实验样本中有920组3个视场被同时正确识别。
2.2 视轴指向辅助视场间星图校正结果分析
进一步分析上一节中含0.07像素星点质心定位误差实验样本的识别结果。如图5所示,1 000组实验样本中至少有1个视场被正确识别的概率为100%,只有2个或1个视场被正确识别的样本组数为80,即135幅待识别星图。
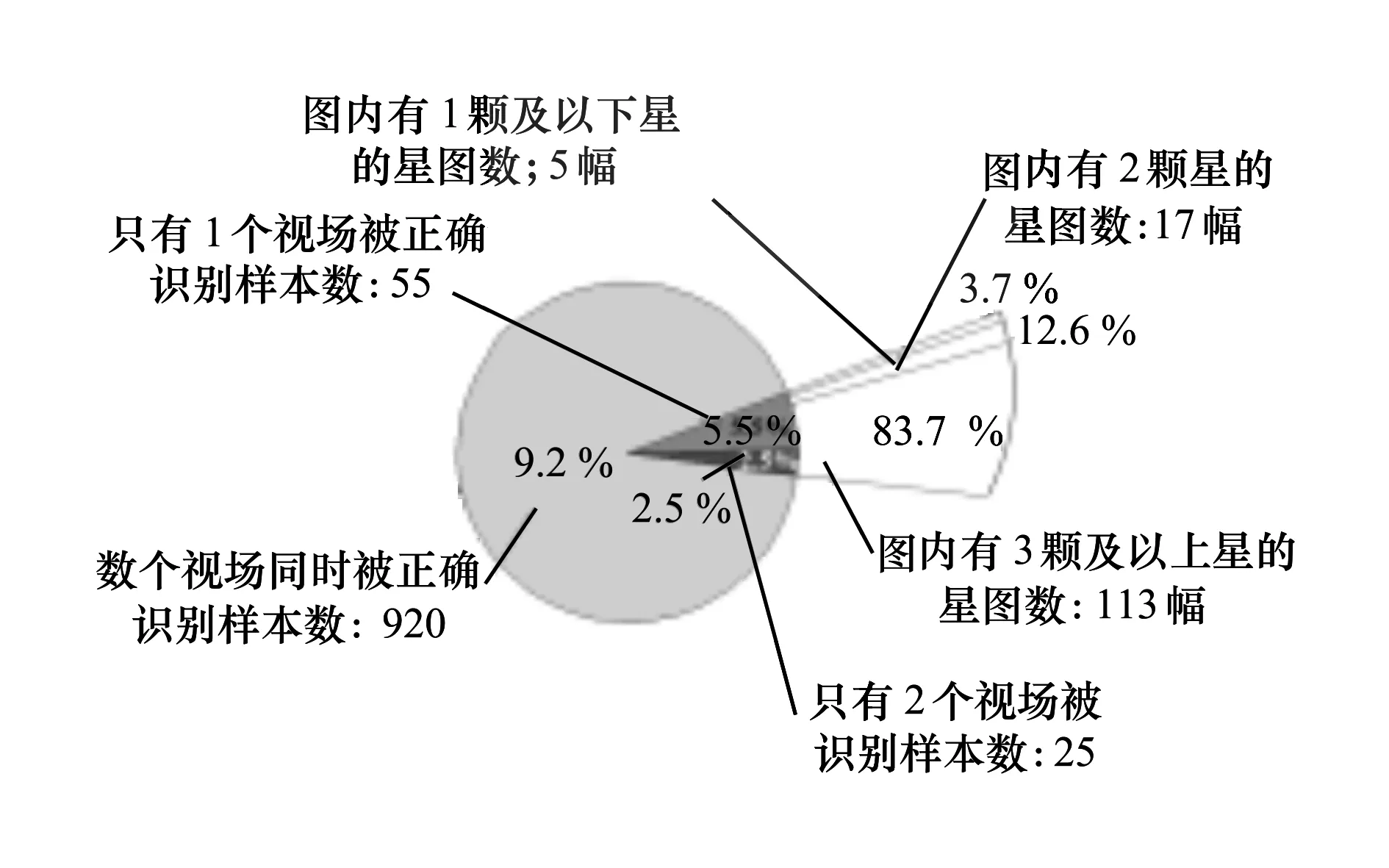
图5 实验样品中各星图内导航星数统计
每组样本利用已正确识别的导航星精确估计视轴指向,并建立局部导航星表进一步完成视场间星图识别与校正。实验结果表明,除了2幅内无导航星的星图外,本算法对20幅只包含有1或2颗导航星的星图全部识别成功,对113幅包含3颗及以上导航星的误识别星图校正成功率达90.3%,该多级星图识别算法使1 000组三视场实验样本的整体识别正确率提升至98.9%。
同时,本节还设计了1组与文献[7]算法的对比实验。实验采用3.1节中的1 000次随机天球指向作为实验样本,文献[7]的视场内星图识别采用三角形匹配算法,用于视场间星图识别的视轴指向信息由仿真的电子指南针设备提供(视轴服从均值为0°,标准差为2°(1σ)的高斯误差)。在相同导航星质心定位误差条件下对比文献[7]算法与本文算法对1 000组三视场实验样本的识别正确率和识别时间。

图6 2种三视场星图识别算法性能对比结果
由图6a)可以看出,随着导航星质心定位误差的增大,文献[7]算法对实验样本的识别正确率也随之下降,这是由于三角形匹配算法对星角距识别特征的变化较敏感。本文算法在训练星图识别网络时就充分考虑了导航星质心定位误差的影响,因此对样本的识别结果优于文献[7]算法。此外,文献[7]算法的平均识别时间为22.956 3 ms,其中视场内星图识别时间18.365 2 ms,视场间星图识别时间4.591 1 ms。本文算法利用正确识别导航星估计的视轴指向极大限制了视场间星图识别时导航星的搜索范围。本文算法的平均识别时间为8.464 5 ms,其中视场内星图识别时间5.632 4 ms;识别结果检测时间0.823 1 ms;视场间星图识别与校正时间2.009 0 ms。
2.3 姿态误差分析
为了分析三视场星敏感器的定姿精度,本实验将该算法应用在轨高度500 km;轨道倾角45°;地理起始点为(0°N,122.119°E)的圆形卫星轨道。星敏感器模拟器工作频率为5 Hz。星图中星点质心提取精度为0.05像素[11]。本实验对比分析了单视场星图与三视场星图的卫星姿态估计差异。

表1 姿态误差均方根误差
由表1可以看出,3个单视场解算的姿态精度相似,视场角的限制,导致滚转轴方向的姿态估计精度明显低于俯仰和偏航轴方向。三视场星敏感器提供估计姿态的星点信息较多且空间分布更均匀,三轴姿态估计的精度也随之提高。偏航、俯仰和滚转姿态估计精度分别为1.205 8″,1.086 7″以及1.201 8″,其中滚转轴姿态精度较3个单视场滚转轴姿态精度分别提升了96.18%,96.19%及96.25%。
3 结 论
本文提出了一种面向三视场星敏感器多级星图识别算法,第一阶段利用神经网络进行视场内星图识别,第二阶段以星库中存储的星间角距信息检验导航星识别结果,当正确识别的视场数小于3时,利用已正确识别的导航星信息计算星敏感器的3个视轴指向;第三阶段利用视轴指向辅助未识别与识别错误的导航星完成识别与校正。与文献[7]相比,本算法的视场内星图识别鲁棒性与识别时间具有明显优势。当星点质心定位误差标准差为0.07像素时,本文算法对实验样本的识别正确率仍保持98.9%,识别时间仅为8.464 5 ms。三视场星图的高识别率与合理的星点分布也使得飞行器偏航、俯仰、滚转姿态精度分别提升为1.205 8″,1.086 7″以及1.201 8″。

