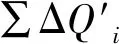基岩深层多滑面抗滑稳定求解方法对比分析
李建波,常 雪,刘苏日
(大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024)

通过对新规范中求解方程分析可知该多滑动面抗滑稳定求解为一个复杂的局部优化问题,本文通过枚举法对解得振荡点进行搜索,局部有效区间进行筛选,结合二分法在有效区间内高效求解。在此基础上提出了遗传算法进行求解,并且对比分析二者之间的计算效率。最后利用有限单元法对本文提出了两种求解方法的准确性进行了验证。
1 多滑动面抗滑稳定分析方法
1.1 多滑动面抗滑稳定方程
新版《混凝土重力坝设计规范》[6](NB/T 35026—2014)中提出了基岩深层滑动面抗滑稳定分析方法。多滑动模式下坝基抗滑稳定计算剖面示意图见图1,图2为其中某一单条块具体受力示意图,多滑动面抗滑稳定分析按以下方法进行计算。

图1坝基抗滑稳定计算剖面示意图
取基岩中某一个滑块体进行受力分析:

图2坝基单条块受力示意图
对每一条块,抗力函数R(·)和作用函数S(·)可表示为:
(1)
Si(·)=(Wi+Gi)sinαi+(ΔHi-ΔUvi)cosαi-ΔQicos(φi-αi)
(2)
定义各条块抗力作用比η如式(3)所示,滑动体系各条块具有同等的抗力作用比η,此时滑动体系达到极限平衡,即坝基整体抗力作用比η,计算公式及要求如下所示:

(3)
考虑分项系数后抗力作用比η′如下:

(4)
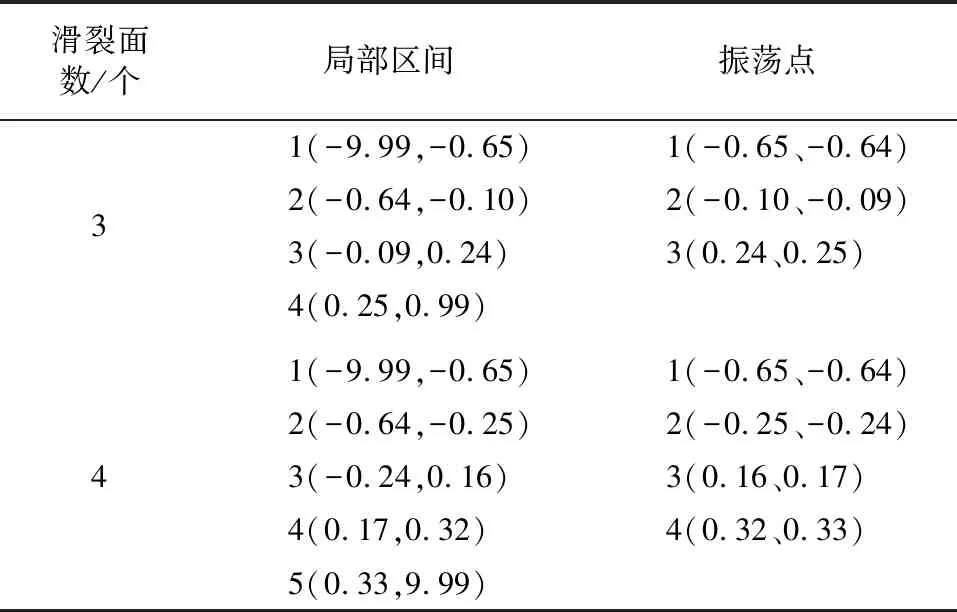
由式(3)可得到n-1个方程,其中含有n个未知数ΔQi,再由坝基体系内力平衡条件可得:
(5)
由式(3)与式(5)联立可以求解得到各滑块侧向接触面间的剪力ΔQi以及抗力作用比η,由式(4)可得η′,当η′≥1时,即认为满足抗滑稳定的要求。
式中各参数的物理意义见表1。

表1 多滑面稳定计算公式中各参数物理意义
1.2 多滑动面抗滑稳定方程求解
1.2.1 枚举法结合二分法局部优化求解
由上述式(3),令ψ=0,假定一抗力作用比η,将该值带入第i个滑块体中可得到该滑块体两侧剪力合ΔQi即:
ΔQi=
(6)
1.2.2 遗传算法求解
与枚举法相比较,遗传算法具有较好的收敛性,计算精度较高,计算时间较短[10-11]。因此本文在枚举法得出结论的基础上同时采用遗传算法进行全局范围内求取最优解的探讨。
遗传算法进行基岩深层多面求解步骤如下:
(1) 种群初始化,在求解区间内生成一维随机数组pop(η)。其中:
ηi=ηmin+rand*(ηmax-ηmin)
(2) 初始种群的适应度评价。定义目标函数:
(7)

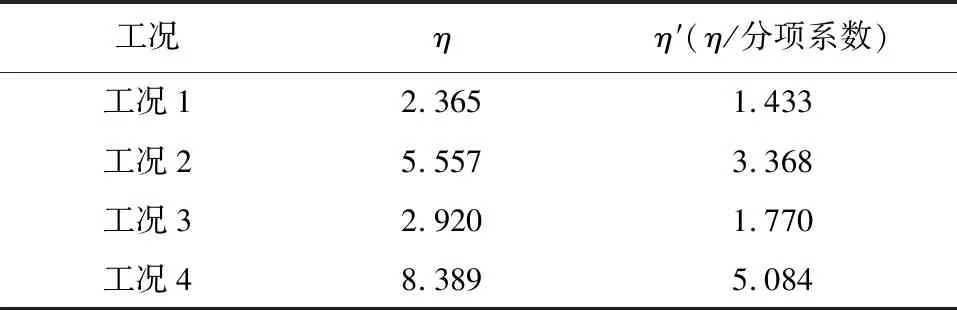
(3) 种群变异。直接对种群进行交叉变异,定义变异概率pc=0.25,交叉因子scalf=0.5。生成随机数,若rand tmpηi=pop(r1)+scalf*(pop(r2)-pop(r3)) 如果tmpηi不在搜索范围内,则变异无效,重新生成随机数r1、r2、r3,进行交叉变异,直至得到的值在搜索区间内。 (4) 对新生成的个体进行适应度评价,若适应度大于原来的个体,则更新种群,令新生成的个体取代原来的个体,并将该个体与当前最优解比较,若适应性超过最优解,则更新当前最优解。在每一代进化中,对种群中所有个体依次进行变异以及种群更新操作。 (5) 重复(2)、(3)、(4),不断更新种群和最优解,直至满足停机条件。 (6) 得到满足精度要求的最优解 本文结合遗传算法采用MATLAB进行编程,具体的计算流程见图3。 图3多滑动面抗滑稳定遗传算法求解流程图 取某一坝体,大坝模型尺寸图见图4,坝体密度2 400 kg/m3、坝基密度为2 700 kg/m3、弹性模量2×1010Pa、帷幕距坝踵10 m、抗剪断摩擦系数1.1、对应的分项系数为1.7、抗剪断黏聚力为1.2 MPa、对应的分项系数为2。将坝基滑动面模拟成3、4个,坝基滑动面参数图分别见图5、图6。将水位设置为满库与半库,在此四种工况下分别用枚举法及遗传算法进行求解。局部枚举法能求出解的振荡点、函数的局部单调区间、有效区间以及方程真解;在此基础上采用遗传算法直接捕捉该多滑动面的有效解。 图4 大坝模型尺寸图 图5 坝基3个滑块 图6坝基4个滑块 对上述两个滑动面,两种荷载信息定义四种工况见表2。 表2 工况信息 采用枚举法分别求得的3、4个滑动面下解得局部区间以及振荡点见表3。 表3 局部区间及震荡点 将公式(6)对η求导可得: (8) 通过枚举法求解分析,得知实际工程中解为跳跃各振荡点后区间连续函数的解,即为实际工程解为方程解的最大值,因此可将上述局部优化问题转换为遗传算法全局求取最大值的优化问题。因此,为快速得到有效解可令遗传算法求解步骤(2)中的放大因子g(η)=lg(η+1.05),通过放大因子直接筛选出符合实际工程的最优解。 由Cost(η)-η图像得∑ΔQi=0的解较明显突出,遗传算法可很快收敛得到最优解。与式(3)结合将得到各工况的解见表5。 表4 基于局部优化算法的多滑动面解 表5 基于遗传算法的多滑动面解 分别对两种求解方法的运算次数进行对比分析,结果见表6,其中各参数的物理意义见表7。 表6 局部优化求解与遗传算法求解计算次数对比 表7 表6中各参数的物理意义 由表6、表7可求得该多滑动面求解中两种算法的计算次数见表8。 表8 两算法计算次数结果对比 由表8可得遗传算法的计算次数较少,当基沿存在较多动裂面时,采用遗传算法计算求解效率明显高于枚举法的局部优化求解。 采用ANASY分别对上述两种滑块体进行建模如图7所示,施加荷载进行有限元分析[13],利用有限元求解公式(9)进行各工况下的多滑动面抗滑稳定求解[14-17],对上述两种方法求解的准确性进行验证。 (9) 图7坝基三个滑动面 有限元进行分析分别求出各滑动面下每个滑移通道的正应力与剪应力后代入公式(9)求得各工况下基岩深层抗滑稳定的抗力作用比系数且与前两种方法对比见表9。 通过有限元法的计算结果与枚举法、遗传算法对比分析,验证了本文中枚举法求解与遗传算法求解的准确性。 表9 三种算法计算结果对比 (2) 由枚举法结合二分法分析的结论可将该局部优化求解转换成遗传算法全局求取最大值的优化求解,进而提高求解效率。 (3) 通过有限元法验证了本文两种求解方法的准确性。
2 算例求解




2.1 枚举法、二分法进行局部优化求解

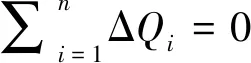
2.2 遗传算法求解

2.3 求解效率对比分析



3 有限单元法验证


4 结 论