考虑攻击程度的城市轨道交通网络抗毁性分析*

冯树民 麻海洲 吕天玲 辛梦薇

(哈尔滨工业大学交通科学与工程学院1) 哈尔滨 150090) (黑龙江省劳动安全科学技术研究中心2) 哈尔滨 150040)

0 引 言

城市轨道交通能够提供相对安全、可靠、便捷、舒适、经济的出行服务，发展轨道交通是解决城市交通拥堵问题的一个重要途径.国内一批大中城市把发展轨道交通纳入城市的总体规划并掀起了轨道交通建设的热潮.起步较早的城市已经建成并在不断完善轨道交通网络，起步较晚的城市也已经拥有或即将拥有少量的轨道交通线路.国内发展轨道交通的强劲势头，促进了越来越多的交通领域的专家和学者认识到研究轨道交通网络运营安全的重要意义.

目前，国内外已有不少学者对轨道交通网络的鲁棒性、脆弱性进行了研究[1-4].Angeloudis等[5]分析了世界主要大城市的地铁统计特征，发现了城市地铁网络具有小世界和无标度网络的特征；乔珂等[6]分析了重要节点失效和线路失效对北京市轨道交通规划路网和目前运营路网的影响；李大愚等[7]从乘客出行延误时间、需求未满足乘客数量两个方面研究连边和站点的重要性，构建了网络服务效率评价指标体系，评价了地铁网络的脆弱性；韩纪彬等[8]重点研究了不同的攻击策略下轨道交通网络的性能，发现了网络对随机攻击具有鲁棒性，对蓄意攻击具有脆弱性，动态攻击策略比静态攻击策略对网络可靠性的影响更大；张晋等[9]构建了北京市轨道交通L空间和P空间网络拓扑结构模型并分析了其特征；孙立山等[10]在大客流冲击背景下，将站点分为功能减弱型和功能中断型，分别用客流传播模型和网络效率模型分析了北京市轨道交通网络的稳定性.

然而，大多数有关轨道交通网络性能的研究是围绕L空间网络拓扑结构进行的，针对P空间网络拓扑结构抗毁性的研究不多.事实上，城市轨道交通P空间网络能够反映换乘的方便程度，具有重要的研究意义.因此，重点分析了L，P空间下的城市轨道交通网络的拓扑结构抗毁性，引入了攻击程度这一构想，将轨道交通网络遭受的攻击程度分为一般攻击和严重攻击.综合考虑单个站点遭受严重攻击后L，P空间网络的平均路径长度、网络效率变化率，以及处于孤立状态的节点数量，结合车站的高峰小时理论最大断面客流量，进行严重攻击下的换乘站脆弱性测算.

1 模型构建

1.1 网络拓扑结构方法

1) L空间方法 轨道交通L空间网络为站点网络，将轨道交通站点看作网络的节点，若两个相邻站点由同一条线路连接，在网络模型中它们之间就有一条边相连，否则不相连.

2) P空间方法 轨道交通P空间网络为换乘网络，将轨道交通站点看作网络的节点，若两个站点存在直达的交通路线，它们之间就有一条边相连，否则不相连.

轨道交通网络由车站和线路组成，拓扑结构图G含有N个节点，邻接矩阵A用{aij}N×N表示，aij描述了图G中节点i和j之间的关系.

aii=0,aij=aij，邻接矩阵为对称矩阵.

图1为由17个站点、三条线路组成的轨道交通网络的L空间和P空间网络拓扑结构图.

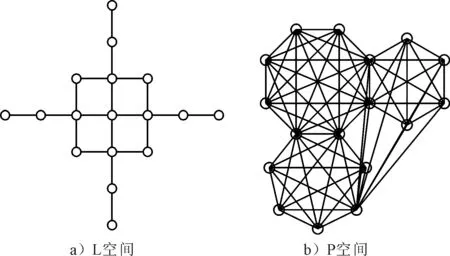
图1 网络拓扑结构图

1.2 攻击策略和攻击程度

1) 攻击策略 基于最大度的攻击策略：对网络中各节点的度进行重要性排序，认为节点的度越大，重要性越高，度越小，重要性相对越低.根据节点的重要性排序，选择网络中度最大的节点并依次对其进行攻击，分析网络在不同数量的节点受到攻击后抗毁性指标的变化规律.

2) 攻击程度 城市轨道交通运营中，由自然因素或人为因素引起的故障可视为遭受外来攻击，不同程度的攻击对网络运营的影响程度不同.在这里，考虑两种针对轨道交通网络的攻击程度：①严重攻击，指节点遭受攻击后功能和作用完全丧失，将会从网络中被移除，意味着如果轨道交通车站受到攻击将不能继续运行，经过该站的线路中断.严重攻击对应的现实情况是轨道故障导致的列车停运；②一般攻击，指节点被移除之后，经过该站点的同一线路保持连通，意味着车站遭受攻击后将处于封闭状态，但列车依然可以通过轨道前往下一个车站，只是不在该站停留.一般攻击对应的现实情况是大客流或其他因素导致的车站临时封闭.

在轨道交通网络的中心节点分别受到严重攻击和一般攻击后，L空间网络拓扑结构见图2，P空间网络拓扑结构见图3.

图2 严重、一般攻击后的L空间网络拓扑结构图

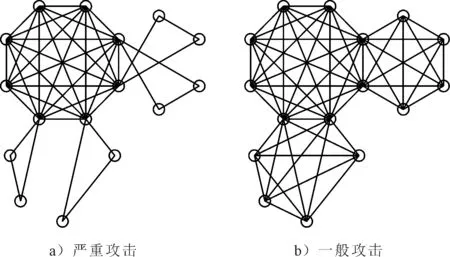
图3 严重、一般攻击后的P空间网络拓扑结构图

1.3 拓扑结构抗毁性评价指标

1) 平均路径长度L定义为网络中任意两节点之间距离的平均值.认为网络中孤立节点与最大连通子图中节点之间的距离为无穷大，此时网络不是连通图.

(1)

式中：N为网络节点总数；dij为节点i和j之间的距离.

针对城市轨道交通，L空间网络的平均路径长度反映任意两车站出行平均所需的单位站间距数；P空间网络的平均路径长度指轨道交通出行所经过线路的数量，反映换乘的方便程度，越小越好.

2) 网络效率E用于衡量网络中节点之间的接近程度，网络效率越小，节点就越疏远.当网络中节点受到攻击之后，网络效率会发生改变，尤其当网络被分割后，网络效率将显著降低.

(2)

3) 网络有效节点减少率ΔS网络中部分节点的失效会导致网络被分割成多个子图，认为最大连通子图中的节点是有效的，遭受攻击的节点和攻击后的孤立节点是无效的.网络有效节点减少率用来描述网络的被分割程度.

(3)

式中：Ni为当网络中有i个节点遭受攻击后最大连通子图的节点数；N为网络正常状态下的节点总数.

1.4 换乘站脆弱性测算方法

1) 理论最大断面客流量 高峰小时车站i的理论最大断面客流量由经过该站的列车数量及列车定员数决定，计算公式为

(4)

式中：j为线路编号；n为线路数量；cj为线路j的列车定员数；mj为线路j高峰小时发车频率.

2) 拓扑结构脆弱性系数 定义网络效率变化率ΔE(i)为

ΔE(i)=E(i)-E

(5)

式中：E(i)为节点i遭受攻击后的网络效率；E为初始网络效率；ΔEL(i)，ΔEP(i)分别为节点i受到攻击后的L空间和P空间网络效率变化率.

定义n(i)为节点i受到攻击后处于孤立状态的节点数量LL(i)，LP(i)分别为节点i受到攻击后L空间和P空间最大连通子图的平均路径长度.

考虑L，P空间网络的平均路径长度、网络效率变化率及孤立节点数，结合高峰时段理论最大断面客流量，可以确定车站i的拓扑结构脆弱性.考虑到参数-ΔEL(i)，-ΔEP(i)，LL(i)，LP(i)和n(i)的量纲不同，采用“min-max标准化”方法对其进行量纲-的量化处理.假设maxA和minA分别为各参数的最大值和最小值，对参数中的任一原始值x进行线性变换处理得到x′，计算公式为

(6)

定义车站i的拓扑结构脆弱性系数为

(7)

3) 换乘站脆弱性 定义换乘站i的脆弱性为

S(i)=I(i)·V(i)

(8)

2 实例分析及讨论

以上海市轨道交通网络为研究对象.截止2017-12-30，上海市已开通运营15条轨道交通线路.针对需出站换乘的换乘站，认为其等同于几个距离较近的普通车站.依据网络运行图对各站点进行编号处理，共计329个车站，其中52个为换乘站，构建L空间下和P空间下的网络拓扑结构图并建立对应的邻接矩阵，运用MATLAB进行仿真分析.

2.1 网络特征值统计与分析

表1为L空间网络特征值.由表1可知，上海市轨道交通网络共有329个站点，每个站点平均与2.27个站点相邻；平均路径长度为15.49，表示任意两站之间平均需要15.49站就能到达；网络直径为41，说明两车站间最远距离为41站；平均聚类系数近似为0，表明网络中节点之间的紧密度较差，体现了轨道交通网络与其他交通网络的不同.

表1 L空间网络特征值

在双对数坐标系下，对度k和度累积分布概率P(k)进行了拟合，拟合结果见图4.拟合曲线表达式为y=3.125 8x-3.074 7,R2=0.871 2，拟合效果较好.上海市轨道交通L空间网络的节点度与度累积分布概率之间存在幂律分布关系，具备无标度网络的特征.

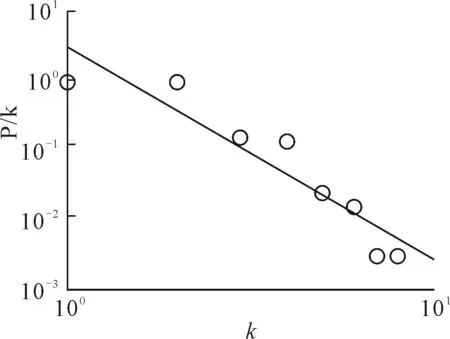
图4 度的累计概率分布

表2为P空间网络特征值，由表2可知，上海市轨道交通无需换乘平均可直达33.23个车站，平均换乘次数为1.15，最大换乘次数为2，换乘较为方便.上海市轨道交通P空间网络具有较小的平均路径长度和较大的平均聚类系数，符合小世界网络的特征.

表2 P空间网络特征值

2.2 连续攻击下的抗毁性分析

2.2.1 L空间

假设L空间网络中3%的度值最大的10个节点依次受到攻击，对应的车站：世纪大道、人民广场、徐家汇、汉中路、陕西南路、东方体育中心、龙阳路、宜山路、曹杨路、镇坪路.

图5为L空间网络平均路径长度变化图.

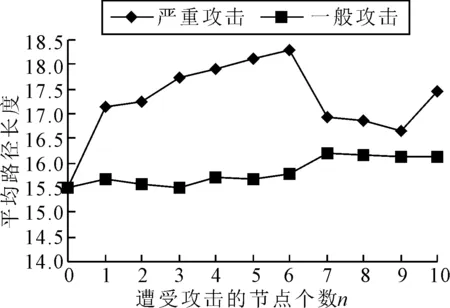
图5 L空间网络平均路径长度变化图

由图5可知，严重攻击后的L空间网络平均路径长度比一般攻击明显要大一些.第一个节点遭受严重攻击后，网络平均路径长度急剧增加，这是因为该节点度值最大且位于网络中心，其失效将显著增加网络中部分节点对之间的最短路径长度，进而影响到整个网络的平均路径长度.当遭受严重攻击的节点个数为n≥4时，网络开始被分割，此时计算的是网络最大连通子图的平均路径长度，随着处于孤立状态的节点越来越多，网络的有效节点越来越少，即规模越来越小，最大连通子图的平均路径长度变化规律难以把握.一般攻击后的网络与正常状态相比，平均路径长度的变化幅度不大.因为一般攻击只是让节点暂时失去了中转功能，线路的整体性没有改变，节点对之间的可替代路径较多.

图6 为L空间网络效率变化图.由图6可知，L空间网络遭受严重攻击后网络效率的下降趋势非常明显，随着遭受攻击的节点数量增加而持续降低；一般攻击后的网络效率降低速度远不及严重攻击.经计算，当10个重要节点全部遭受攻击后，一般攻击、严重攻击后网络效率分别下降了5.29%和51.9%.第4个节点受到严重攻击后网络效率降低幅度明显增大，因为此时的网络被分割成多个子图，不同子图中的节点之间失去了联系，距离变为无穷大，从而严重影响了网络效率.因此，严重攻击对网络造成的破坏作用远大于一般攻击.

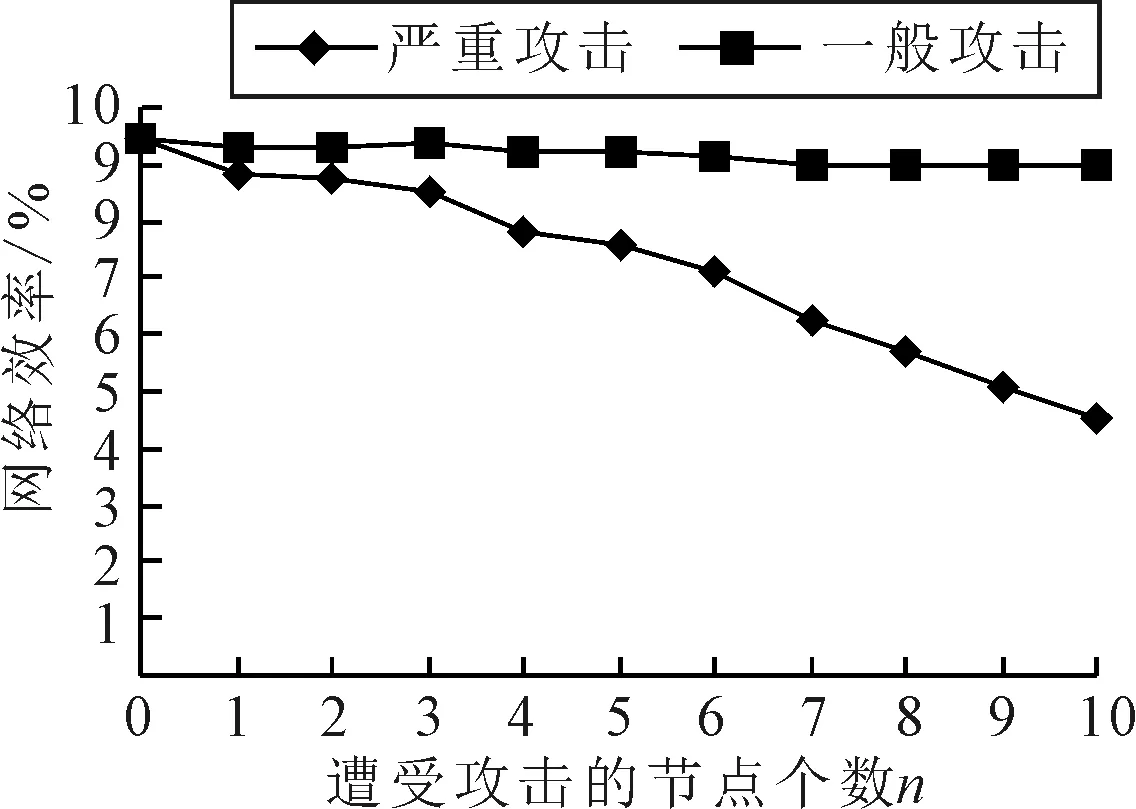
图6 L空间网络效率变化图

图7为L空间网络有效节点减少率变化图，由图7可知，L空间网络有效节点减少率随着遭受攻击的节点数量增加而持续增大，意味着有效节点数量越来越少.当n≤3时，严重攻击和一般攻击后的网络有效节点减少数量都等于遭受攻击的节点数量且线性缓慢增加，说明此时网络没有因节点遭受攻击而被分割.当n≥4时，一般攻击后网络失效节点数量保持线性缓慢增加；严重攻击后网络被分割，孤立节点越来越多导致失效节点数量骤增.相对一般攻击，严重攻击更容易破坏网络的完整性.

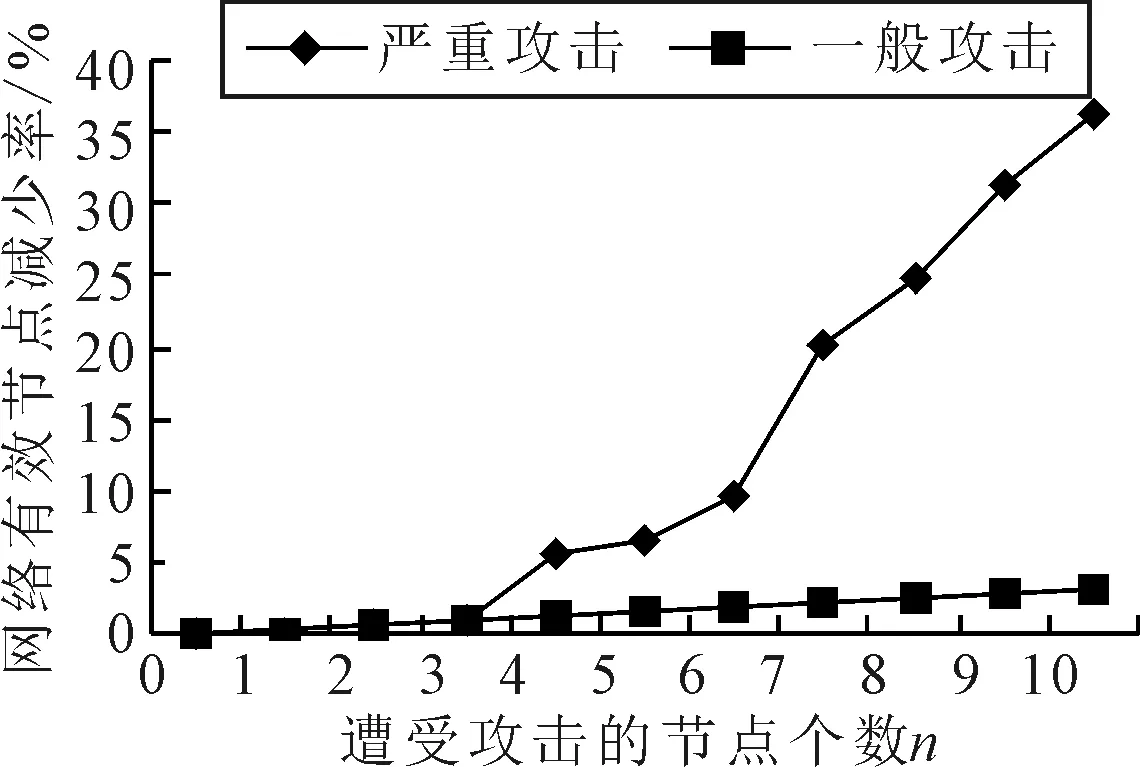
图7 L空间网络有效节点减少率变化图

2.2.2 P空间

假设P空间网络中3%的度值最大的节点依次受到攻击，对应的车站：世纪大道、徐家汇、东方体育中心、人民广场、陕西南路、曹杨路、宜山路、镇坪路、汉中路、虹桥路.

图8为P空间网络平均路径长度变化图，由图8可知，P空间网络中的重要节点依次遭受攻击后，网络平均路径长度呈增大趋势.一般攻击后网络平均路径长度缓慢增大，总体变化不大；严重攻击后网络平均路径长度急剧增大.经计算，当网络中10个重要节点全部遭受攻击后，一般攻击、严重攻击后平均路径长度分别增加了15.67%和69.89%.严重攻击对网络平均路径长度的影响程度远大于一般攻击，主要因为节点遭受严重攻击后导致其所在线路发生中断进而变为两条线路，一般攻击则不会破坏线路的完整性.严重攻击会显著增加轨道交通出行的平均换乘次数，使出行时间延长.

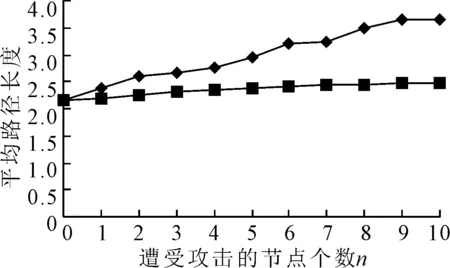
图8 P空间网络平均路径长度变化图

图9为P空间网络效率变化图，由图9可知，P空间网络效率随遭受攻击的节点数量增加呈下降趋势.一般攻击后网络效率缓慢下降；严重攻击后网络效率骤降，紧密度变差.经计算，当网络中10个重要节点全部遭受攻击后，一般攻击、严重攻击后P空间网络效率分别降低了10.33%和60.46%.严重攻击对网络效率的危害更大.

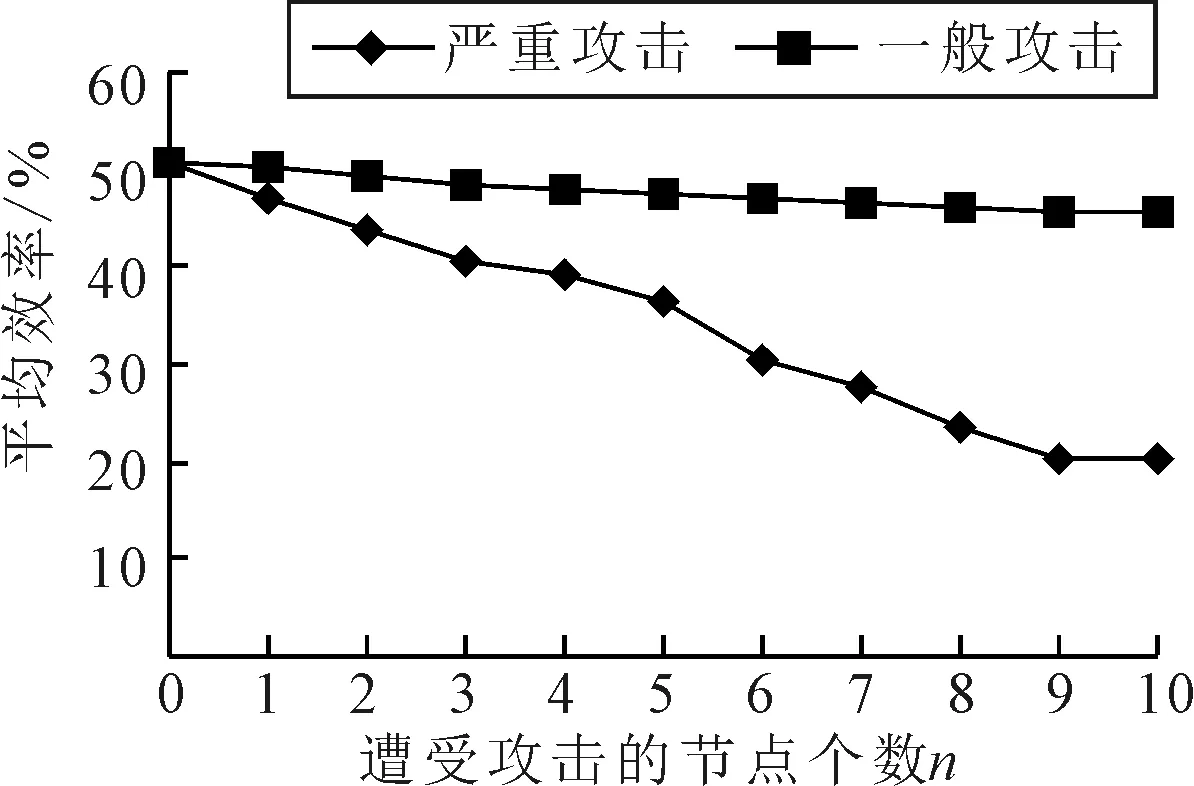
图9 P空间网络效率变化图

图10为P空间网络有效节点减少率变化图，由图10可知， P空间网络中3%的度值最大的节点依次受到攻击后，网络中有效节点减少率不断增大，即失效节点数量不断增加.一般攻击后失效节点数量缓慢增加；严重攻击后失效节点数量迅速增加.这是因为节点受到严重攻击后网络中处于孤立状态的节点越来越多.经计算，当网络中10个重要节点全部遭受攻击后，一般攻击、严重攻击后P空间网络有效节点分别减少了3.04%和24.62%.

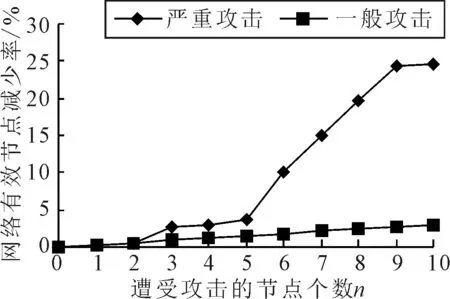
图10 P空间网络有效节点减少率变化图

2.3 换乘站脆弱性测算与分析

换乘站在轨道交通网络运营中发挥着重要作用，在高峰时段内承受较大的客流压力，承担的运营风险更高.表3为上海市轨道交通网络中脆弱性最大，也就是抗毁性最差的10个换乘站.

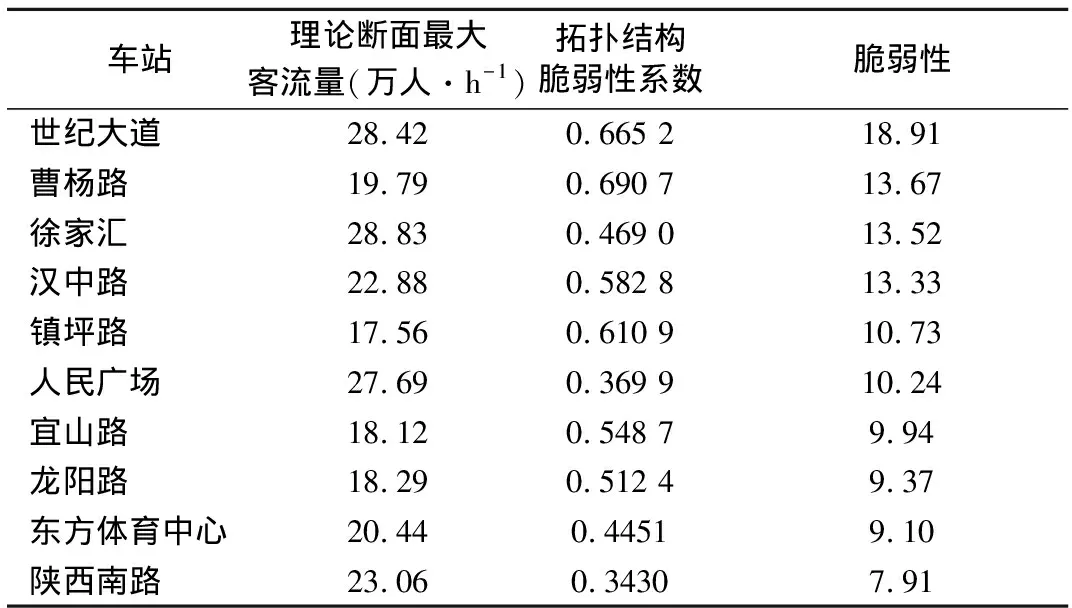
表3 上海市轨道交通网络换乘站脆弱性

由表3可知，上海市轨道交通网络中抗毁性最差的10个换乘站普遍具有较大的理论最大断面客流量和拓扑结构脆弱性，世纪大道站具有最大的脆弱性，抗毁性最差，曹杨路、镇坪路、宜山路和龙阳路的理论最大断面客流量相对较小却具有相对较大的拓扑结构脆弱性，所以也表现出较差的抗毁性.这些换乘站一方面有利于提升网络的连通性，一方面由于承受较大的客流压力增加了安全隐患，在发生严重故障后将对整个网络的运营产生巨大的不良影响.因此，在日常的运营过程中，应加强对抗毁性较差的换乘站的安全管理和维护工作.

3 结 论

1) 基于复杂网络理论构建了城市轨道交通网络抗毁性分析模型，从L空间和P空间两种状态下量化分析了度值较大的节点分别遭受严重攻击和一般攻击后，网络拓扑结构抗毁性的变化规律；提出了一种综合考虑拓扑结构脆弱性和理论最大断面客流量的换乘站脆弱性测算方法.

2) 统计分析了上海市轨道交通网络的特征值：L空间下，具有较小的聚类系数，网络覆盖范围广，紧密性较差；P空间下，具有小世界网络的特征，换乘次数少，换乘较为方便.

3) 上海市轨道交通网络网络对严重攻击表现出较差的抗毁性，对一般攻击表现出较强的抗毁性.应做好安全评估与危险防范工作，降低重要节点发生严重故障的风险概率；面对严重攻击抗毁性表现最差的10个换乘站，应重视对其进行安全管理和维护，提高安全管理和应急水平.