双排桩支护结构的抗倾覆稳定性计算方法研究

雷 晗

（上海市政工程设计研究总院(集团)有限公司，上海市 200092）

0 引言

近年来随着城市基础设施建设的推进，城市地下空间结构快速发展，各种新的基坑支护结构形式不断涌现。但基坑支护引发的问题也日益增多，基坑支护的可靠性和经济性也面临越来越多的社会关注。

双排桩支护结构是一种新型的支护结构。它是由前、后两排平行的钢筋混凝土桩、压顶梁，以及前后排桩之间的连梁形成的空间门式刚架结构。与单排悬臂桩相比，双排桩的抗侧移刚度大，变形控制能力强；与锚拉式支护结构相比，双排桩不占用基坑外地下空间，对周边环境的影响小；与支撑式支护结构相比，双排桩在基坑内不设支撑，为土方开挖和主体结构施工提供了较大的施工空间，施工速度快。因此，双排桩支护结构在各种大型深基坑工程中得到了较为广泛的应用[1-2]。

国内一些学者对双排桩支护结构进行了比较深入的研究，并取得了一定的研究成果，如：何颐华[3]根据前后排桩之间的滑动土体占桩后滑动土体总量的体积比例来确定前后排桩所受侧向压力，并对不同的布桩形式给出了相关的计算公式；黄强[4]认为后排桩的存在改变了土体滑裂面的形态，并运用极限平衡原理计算主动土压力；刘钊[5]采用Winkler假定，考虑桩土的共同作用确定出前、后排桩在开挖面以上的土压力荷载及地基土的水平基床系数；郑刚[6]等人提出将双排桩之间的土视为薄压缩层，并以水平向弹簧模拟，可以考虑两排桩之间的土层分布变化、压缩性、桩间土加固等对双排桩相互作用的影响，避免对前、后排桩土压力做出人为的分配；吴刚[7]等人考虑了滑移面和排距对作用在前后排桩上的土压力的影响，在弹性地基梁法的基础上，提出了一种新的双排桩支护结构设计计算模型。根据前后排桩的土压力分布和桩端嵌固情况，上述研究中的计算模型主要可分为3类：一类是基于经典土压力理论确定的计算模型；一类是基于winkle假定的计算模型；一类是基于土拱理论和土抗力法建立的计算模型[8]。这三类计算模型都在不同程度上讨论了土压力作用在前后桩体上的分布规律，但其分析焦点一般为桩体的受力特性，对双排桩的抗倾覆稳定性却并未做深入研究。本文在已有计算模型的基础上，采用弹性抗力法，结合相关工程的实测资料，对双排桩支护结构抗倾覆安全系数的计算方法进行了改进。

1 计算模型

1.1 国标计算方法

《建筑基坑支护技术规程》（JGJ120—2012）[9]（以下简称《规程》）中规定，对双排桩支护结构，宜采用平面杆系结构弹性支点法进行分析，即弹性抗力法。弹性抗力法采用连续布置、且相互独立的土弹簧模拟桩周土体对桩的作用，前后排桩体视为竖直放置的弹性地基梁，如图1所示，地基基床系数按“m”法确定，即：

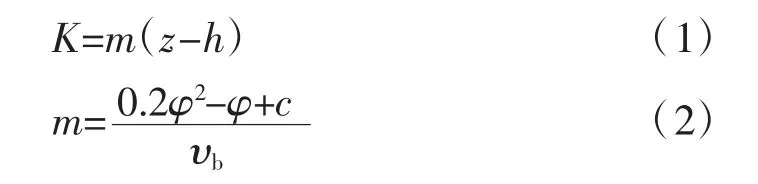
式中：m为地基水平抗力比例系数，一般按桩的水平荷载试验及地区经验取值，在缺少试验和经验时，也可按上述经验公式计算；z为计算点的深度；h为计算工况下的基坑开挖深度；c、φ分别为土的黏聚力、内摩擦角；υb为坑底处的水平位移量，当此处的水平位移不大于10mm时，可取10mm。

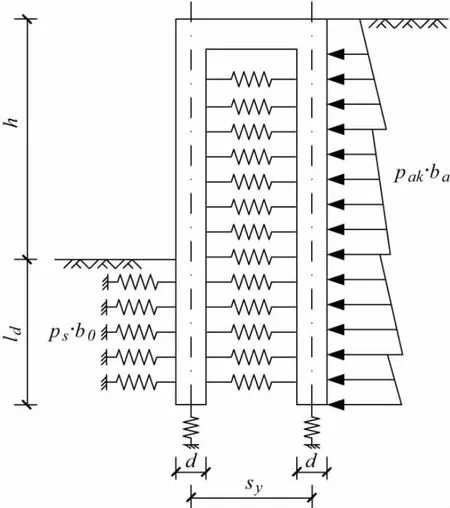
图1 双排桩计算模型

双排桩的抗倾覆稳定性计算模型如图2所示，安全系数按下述方法进行计算：

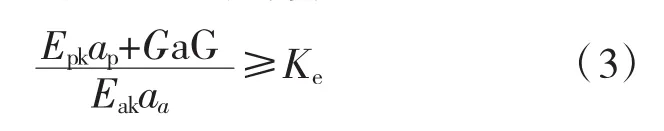
式中：Eak、Epk分别为基坑外侧主动土压力、基坑内侧被动土压力标准值；aa、ap分别为基坑外侧主动土压力、基坑内侧被动土压力合力作用点至双排桩底端的距离；G为双排桩、刚架梁和桩间土的自重之和；aG为双排桩、刚架梁和桩间土的重心至前排桩边缘的水平距离；Ke为嵌固稳定安全系数，安全等级为一级、二级、三级的双排桩，Ke分别不应小于 1.25、1.2、1.15。

根据公式（3）可知，《规程》中一方面假定双排桩支护结构绕前排桩的底部转动，另一方面又假定双排桩支护结构在土压力作用下向基坑内侧产生整体平移，且在极限破坏状态时产生的位移量使外侧土压力减小为主动土压力、内侧土体反力增大至被动土压力。

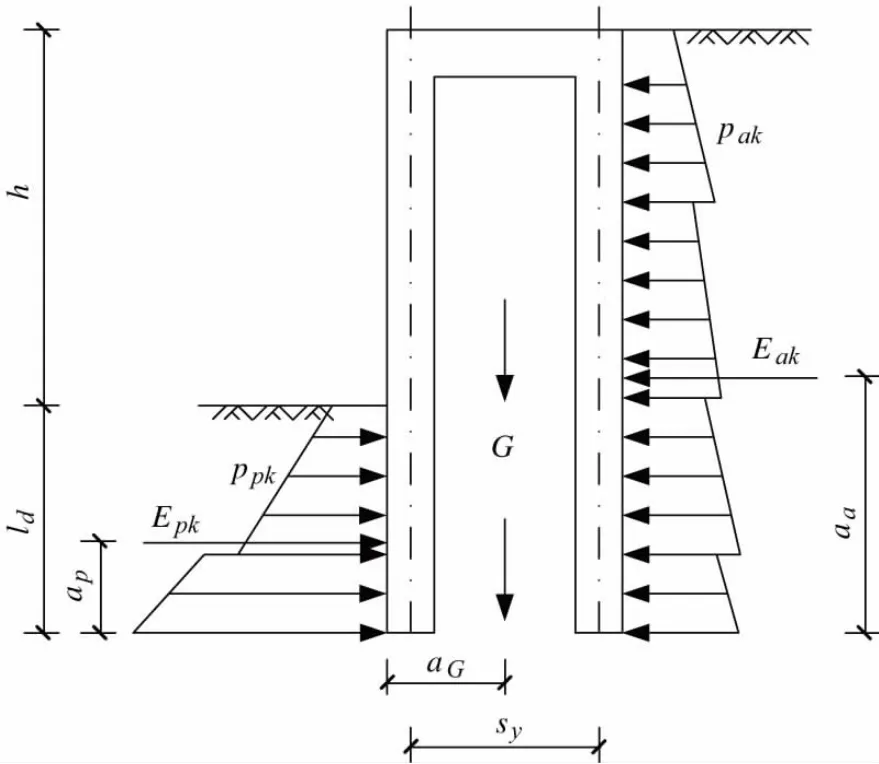
图2 双排桩抗倾覆稳定性计算图示

实践表明[10]，土体负位移为坑深的1‰～8‰时达到主动状态，正位移为坑深的1%～5%时，则为被动状态。以基坑深度8 m为例，达到主动状态的位移为-8～-64 mm，达到被动状态的位移为80～400 mm。

根据国内学者的研究和相关工程的实测资料[7]，双排桩作为一种悬臂结构，桩体侧向位移与深度呈反比关系，后排桩的位移量已足以使外侧土压力达到主动状态，而位于坑底以下的前排桩侧向位移近似呈抛物线形。在土压力作用下，双排桩并不会产生整体平移，如图3所示，基坑内侧土体的变形为上大下小，即更接近于绕前排桩的底部转动，在同种土层条件下，越接近坑底的位置土体越易发生被动破坏，因此《规程》中的假定存在与实际不符的情况。

1.2 抗倾覆计算方法修正

当双排桩支护结构发生倾覆时，一般情况下桩顶侧向变形最大，桩底侧向变形最小，因此假定坑底处的土体达到被动状态，桩底处的土体不发生变形。根据弹性抗力法，可得：

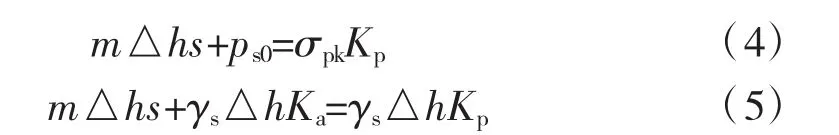
式中：△h为坑底处的单位深度，可取△h=0.1 m；s为坑底处前排桩的侧向变形；σpk为基坑内侧计算点的土中竖向应力；γs为基坑内侧土体的容重；ps0为初始分布土反力；Ka、Kp分别为主动土压力系数、被动土压力系数。式中未考虑黏聚力c的影响，实际计算时可按坑底被动土压力相等的原理将其折算为等效内摩擦角进行考虑。

位于坑底以下的前排桩侧向位移近似呈抛物线形，抛物线的曲率与m值相关，为便于分析，暂按直线型进行计算，即基坑内侧位于坑底以下i点的侧向变形为：

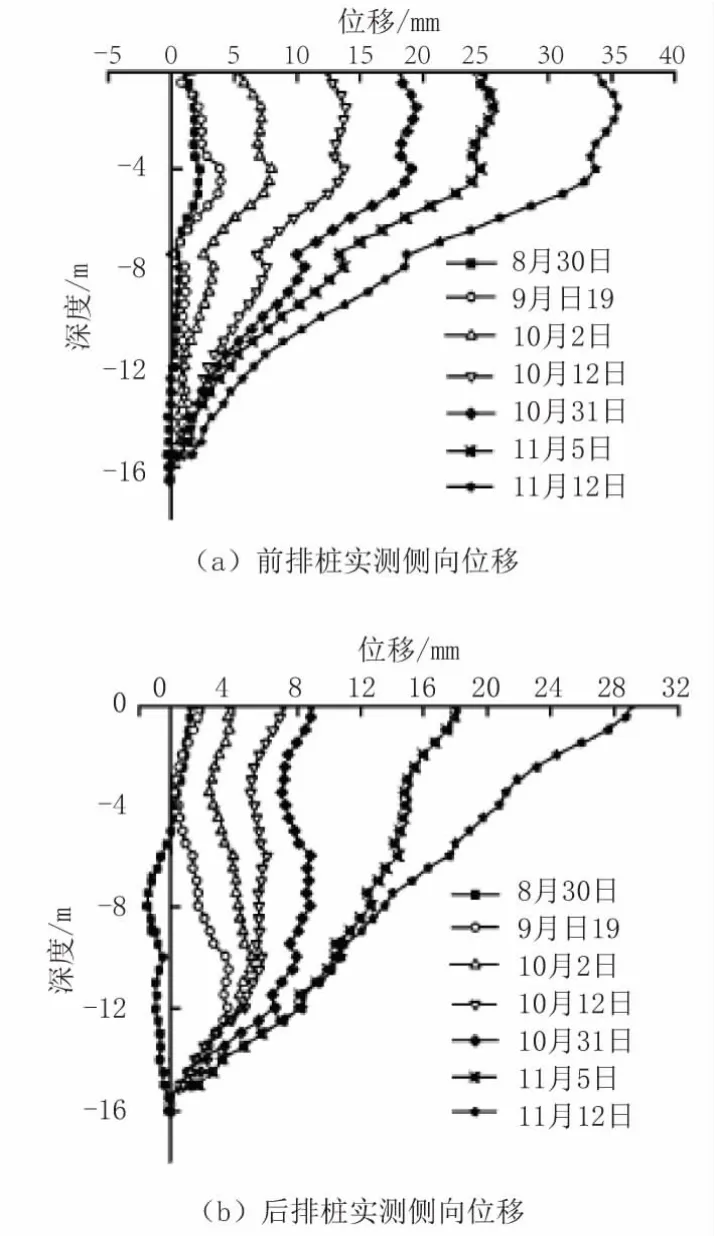
图3 双排桩变形实测数据曲线图

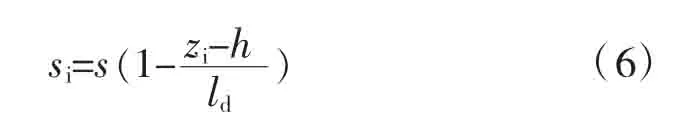
i点的土体抗力为:

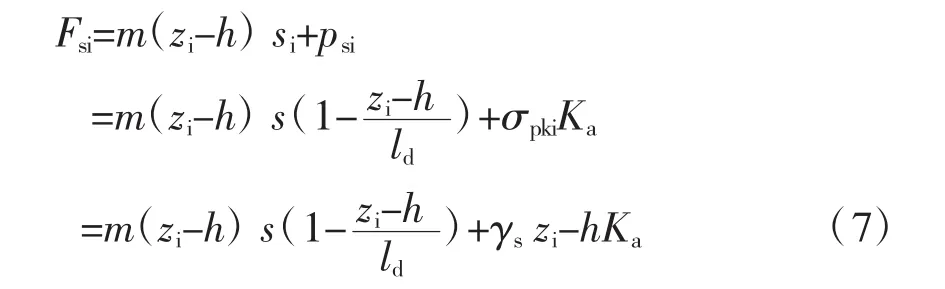
同时，Fsi需满足以下条件：

基坑内侧的抗力合力为：

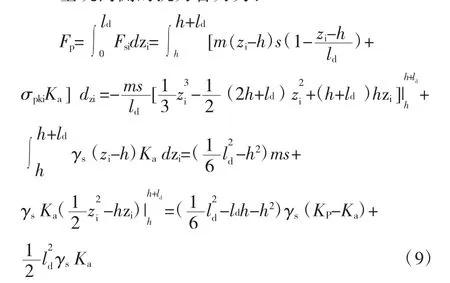
式中：zi为i点相对于地面的深度；ld为桩插入深度；zi为i点的深度；psi为i点的初始侧向土压力；σpki为i点的竖向应力。

因此，经修正的双排桩抗倾覆稳定性安全系数应按下述公式进行计算：

式中：ap为基坑内侧土压力合力作用点至双排桩底端的距离，由于内侧土体抗力为抛物线分布需通过积分进行计算。

1.3 计算结果比较

为便于比较修正公式与《规程》的差异，取一算例进行对比。基坑围护的主要设计参数为：（1）基坑开挖深度h=8 m，安全等级为二级，采用双排钻孔灌注桩围护，前后排桩的桩径均为0.8 m，间距1 m，桩插入深度ld=8 m，前后排中心距sy=4 m，混凝土标号C30，刚架梁采用1 m×1 m；（2）土层采用均质土，土体容重γs=18 kN/m3，黏聚力c=0，内摩擦角φ=30°。

对上述算例采用有限元软件Plaxis模拟，模型如图4所示。计算采用平面应变模型，灌注桩采用梁单元模拟，土体采用三角形单元模拟，桩土之间考虑接触面，土体本构关系采用莫尔-库伦模型。

图4 有限元计算模型

图5为按式（7）计算的基坑内侧土体反力与有限元计算结果及被动土压力的对比，由图5可见，修正公式与有限元计算的结果较为接近，两者均为中间大两边小，变化趋势基本一致，最大土体反力均在120 kPa左右。而在靠近坑底处，有限元计算结果比修正公式计算结果大，这是由于有限元模型中坑内土体与坑外土体是连续体，坑内土压力也与坑外土压力互相协调。

与被动土压力相比，修正公式计算的土体反力在靠近坑底处基本接近被动土压力，但在桩底处的土体反力则仍保持为主动土压力。随着深度的增加，由于桩体侧向变形越来越小，修正公式计算的土体反力出现明显的反弯点，与被动土压力之间的差距也逐渐变大。

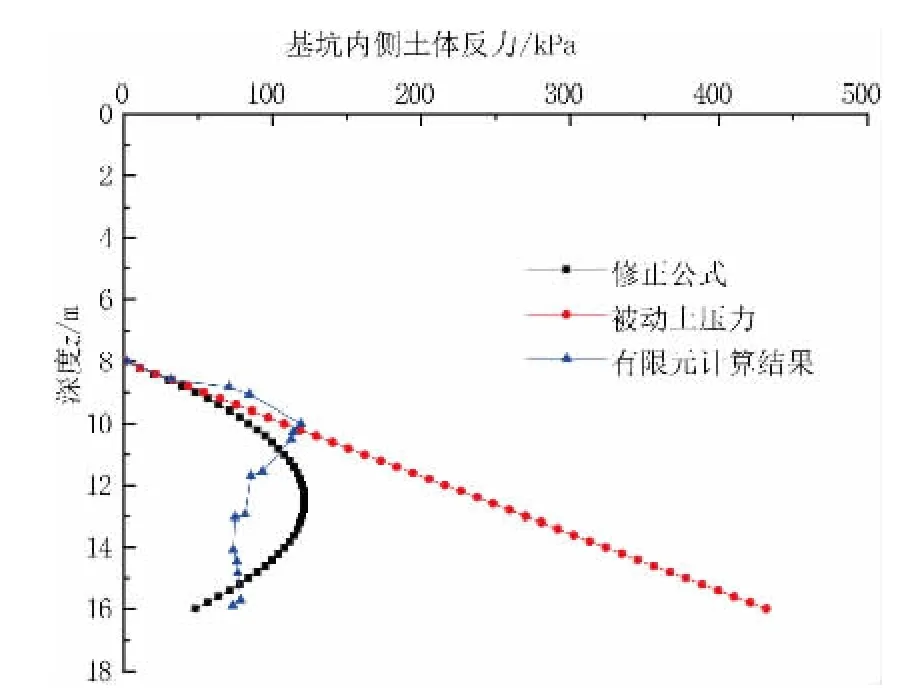
图5 基坑内侧土体反力分布曲线图

2 参数影响分析

根据上文中的公式分析，对双排桩抗倾覆稳定性安全系数造成差异的参数主要有 h、ld、c、φ等。为便于比较，对于不影响差异的参数，仍按上述算例采用常值。

2.1 基坑深度h的影响

保持ld、c、φ等参数不变，基坑深度h=4～12 m时抗倾覆稳定性安全系数的变化见图6所示，《规程》和修正公式计算的安全系数变化范围分别为4.259～1.144、3.074～0.888。由图 6 可见，随着基坑深度的增加，安全系数均呈双曲线型逐渐减小，前者为后者的1.29～1.38倍，但两者的差距逐渐缩小。

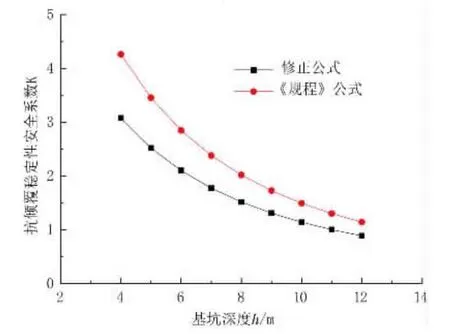
图6 基坑深度h对抗倾覆稳定性安全系数的影响曲线图

2.2 排桩插入深度ld的影响

保持h、c、φ等参数不变，基坑深度ld=2～12m时，ld/h=0.25～1.5，抗倾覆稳定性安全系数的变化见图7所示。《规程》和修正公式计算的安全系数变化范围分别为 1.867～2.512、1.516～2.346。由图 7 可见，随着插入深度的增加，安全系数均呈先减小后增大的趋势，且两者的差值呈递增趋势，前者为后者的1.01～1.52倍。在ld/h较小时，两者比较接近；而在ld/h较增大到1.5时，两者的差值达到1.52倍左右。这是由于在ld/h较小时，土体反力较接近，同时自重G起主要控制作用；而随着ld/h的增大，土体反力逐渐占据控制地位。安全系数的变化趋势均出现明显的反弯点，前者的反弯点出现在ld/h=0.75附近，而后者的反弯点明显后移，出现在ld/h=1.0附近。

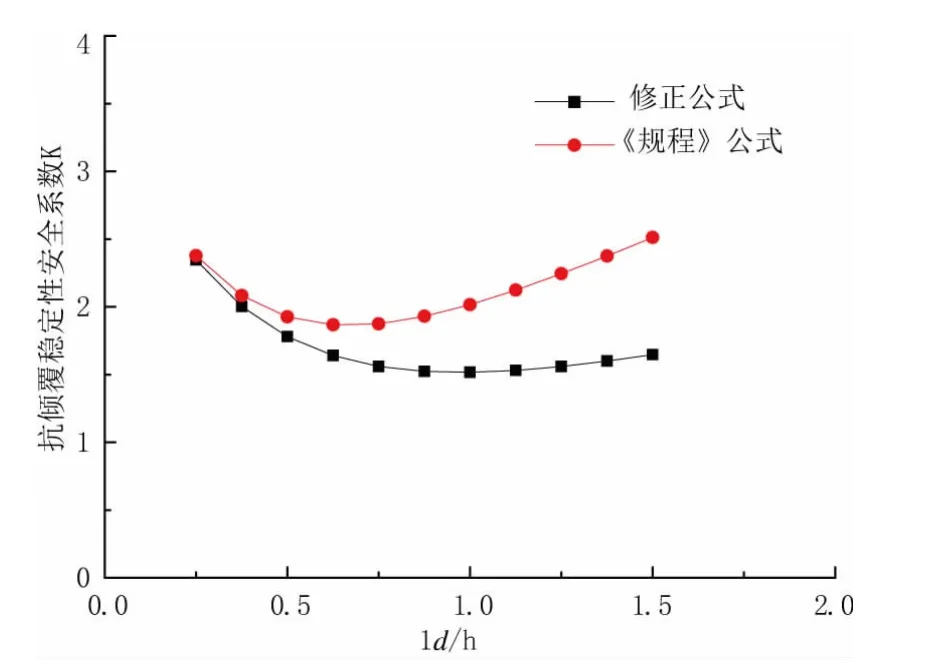
图7 插入深度ld对抗倾覆稳定性安全系数的影响曲线图

2.3 内摩擦角φ的影响

保持 h、ld、c、等参数不变，内摩擦角 φ=15～40°时，抗倾覆稳定性安全系数的变化见图8所示。《规程》和修正公式计算的安全系数变化范围分别为 0.865～4.009、0.747～2.750。由图 8 可见，随着内摩擦角的增加，安全系数均呈双曲线型逐渐增大，前者为后者的1.16～1.46倍，但两者的差距逐渐增大。

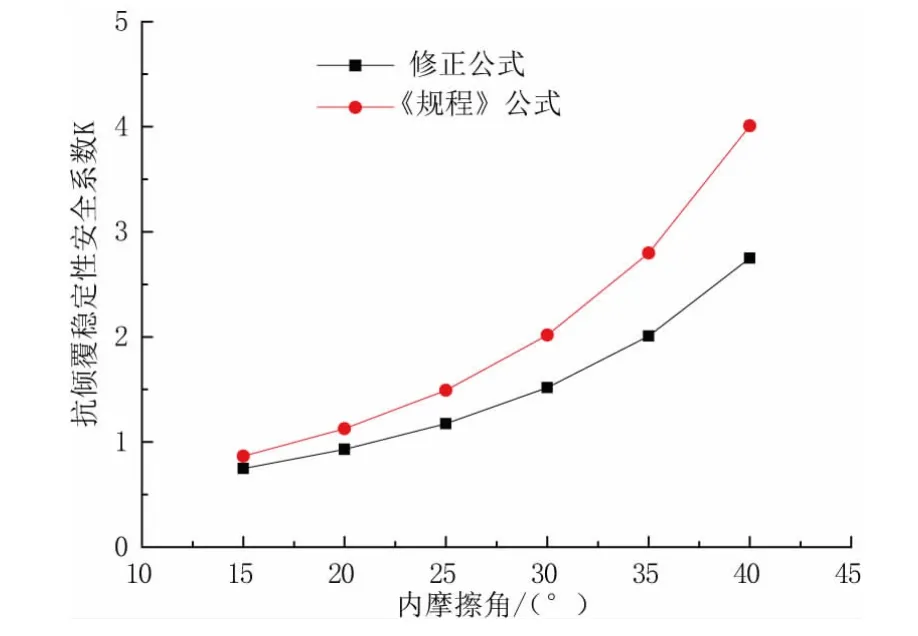
图8 内摩擦角φ对抗倾覆稳定性安全系数的影响曲线图

2.4 黏聚力c的影响

保持h、ld、φ等参数不变，黏聚力c=0～30 kPa时，将其折算为等效内摩擦角进行计算，即：

φd=2tan倾覆稳定性安全系数的变化见图9所示。《规程》和修正公式计算的安全系数变化范围分别为2.016～5.214、1.516～2.616。由图 9 可见，随着黏聚力的增加，安全系数近似呈线性增大，两者的差距也逐渐增大，前者为后者的1.33～1.99倍。

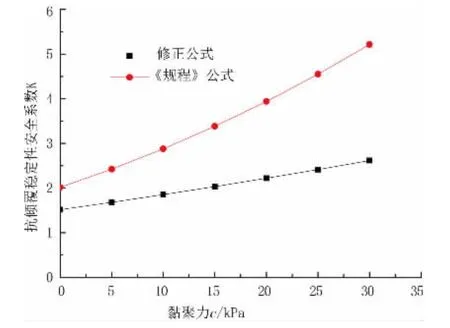
图9 黏聚力c对抗倾覆稳定性安全系数的影响曲线图

综上分析，由于修正之后的土压力曲线图与被动土压力相差较大，采用被动土压力计算显然偏于危险，因此建议采用m法进行修正计算。根据上述对比，h、ld、c、φ等参数对双排桩抗倾覆稳定性安全系数均影响显著，且修正公式与《规程》公式相差较大，两者的倍数在1.01～1.99之间，在采用修正公式后，相应地可将安全系数降低，从而与采用被动土压力计算具有同等安全度，建议一级、二级、三级基坑的抗倾覆稳定性安全系数可分别取1.1、1.05、1.0。

3 结论

通过以上分析，可得到以下结论：

（1）在土压力作用下，双排桩支护结构并不会产生整体平移，基坑内侧土体的变形为上大下小，更接近于绕前排桩的底部转动，在同种土层条件下，越接近坑底的位置土体越易发生被动破坏；

（2）本文采用m法得出了基坑内侧土体反力的修正公式，土压力分布为中间大两边小，出现明显的反弯点。修正公式计算的土体反力在靠近坑底处基本接近被动土压力，但在桩底处的土体反力则仍保持为主动土压力，这与有限元分析结果接近，而与被动土压力值相差较大。

（3）在m法的基础上推导出抗倾覆稳定性安全系数的修正公式，h、ld、c、φ 等参数对其影响显著，且修正公式与《规程》公式相差较大，建议采用修正公式计算的一级、二级、三级基坑的抗倾覆稳定性安全系数可分别取1.1、1.05、1.0。