一种无人飞行器监控数据预处理方法

(中国洛阳电子装备试验中心， 河南济源 454650)

0 引言

近年来，随着航空业、自动控制及微电子技术的迅猛发展，无人机的性能不断提高，其在军民航各方面的应用得到了广泛的共识，无法实时动态监控、飞行调配困难等随之而来的不安全因素也逐渐增多[1]。空管系统是一种有效监控有人驾驶航空器的自动化平台，但是对无人飞行器的监控数据并不兼容，本文提出一种基于自适应卡尔曼(Kalman)滤波的无人飞行器监控数据预处理方法，将来自各传感器监测无人飞行器的航迹数据通过一系列变换和平滑滤波，统一数据格式后，发送到空管系统指挥中心进行显示，确保各类无人飞行器的监控数据能够被空管系统兼容，从而达到对数据的有效利用。

1 预处理流程设计

预处理流程设计如图1所示，系统接收到各类监控设备的无人飞行器数据后，首先通过数据帧判别无人飞行器的类型，接下来从遥测信息帧中提取出目标的位置信息并进行坐标变换，之后对各航迹数据进行野值判别、剔除与平滑滤波，最后按照空管系统的标准格式对无人飞行器航迹信息进行封装，将数据发送到空管系统指挥中心进行显示。

2 空间对准

所谓空间对准就是把接收到的传感器数据变换到一个公共的空间参考系上[2-3]，以便与目标数据库或航迹文件中的其他测量数据融合。某指挥中心接收到的数据中主要使用大地直角坐标系、极坐标系和参考点直角坐标系等几种类型的坐标参考系，它们是独立的测量，并且参考点直角坐标系根据目标测量设备的不同，参考点的选取也是不一样的，所以数据融合前要对所有数据进行空间对准。针对该指挥中心的情况，主要是接收到数据时先对所有数据进行坐标转换，将所有的数据统一到大地直角坐标系下进行融合计算，并尽量地压缩算法，减少转换次数，在地图显示前转换到参考点坐标系和极坐标系，实时准确地显示目标航迹。

3 基于改进“当前”统计模型的自适应Kalman目标滤波算法

为提高对目标的跟踪精度，指挥中心对接收到的各传感器探测目标航迹数据进行平滑滤波，以获得每条航迹的最佳估计值，确定最终的航迹。根据无人飞行器的飞行特点，其在飞行过程中一般沿预订航线作匀速或匀加速直线运动，但也可能出现某些机动，如缓慢转弯、遇到阵风或大气湍流等，因此指挥中心采用自适应Kalman滤波算法对无人飞行器的航迹进行滤波处理，得出目标状态信息的最优估计值，以提高跟踪监视的精度。平滑滤波的关键是跟踪设定的目标模型与实际的目标动力学模型的匹配问题，常用的目标跟踪模型包括CV、CA、Singer、“当前”统计模型等[4-5]。

CV和CA模型只适用于跟踪匀速和匀加速直线运动目标，Singer模型中许多参数需预先设定，在实际中很难实现，“当前”统计模型是目前公认的一种较为符合实际的运动模型，该模型能够根据目标的“当前”加速度对机动加速度方差进行自适应地调整，进而对状态噪声协方差矩阵自适应调整。

3.1 基于“当前”统计模型的自适应Kalman目标滤波算法

无人飞行器运动的离散时间系统状态方程可表示为

(1)

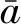
(2)

(3)

(4)

(5)

式中，T为采样周期，α为机动频率。

离散时间观测模型可表示为

Z(k+1)=H(k+1)X(k+1)+V(k+1)

(6)

式中，H(k+1)为测量矩阵，V(k+1)为零均值高斯白噪声序列，其协方差为R(k+1)。

基于“当前”统计模型的Kalman滤波算法的基本步骤为：

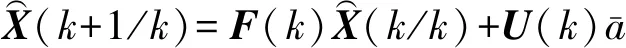
(7)

2) 根据前一次得到的滤波误差方差阵P(k/k)计算预测误差方差阵：

P(k+1/k)=F(k)P(k/k)FT(k)+Q(k)

(8)

3) 计算Kalman增益：

K(k+1)=P(k+1/k)HT(k+1)[H(k+1)P(k+1/k)HT(k+1)+R(k+1)]-1

(9)

4) 计算滤波估计值：

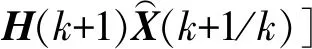
(10)

5) 计算滤波误差方差阵：

P(k+1/k+1)=[I-K(k+1)H(k+1)]·

P(k+1/k)

(11)

只要给定滤波初值X(0/0)和P(0)，在任意时刻，根据量测值Z(k)，就可以递推出该时刻的状态估计值X(k/k)。

3.2 改进算法模型

本文提出一种改进的算法，根据当前加速度的大小给出当前最大加速度，根据滤波新息的变化，自适应调整机动频率，实现对目标更为精确的跟踪。

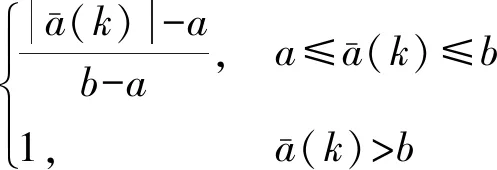
a=0,b=3

(12)

则当前最大机动加速度为

(13)

F(k)和Q(k)都是机动频率α的函数。所以可以通过改变α来调整F(k)和Q(k)，能使其更符合目标的真实运动状态。

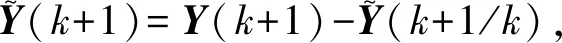
(14)

3.3 仿真验证

为了验证改进后算法的性能，下面对某无人飞行器的一段匀速—匀加速—匀速运动进行仿真分析，假设飞行器起点坐标为坐标原点，在1～50 s作X,Y向的速度均为100 m/s的匀速直线运动，在51～80 s作X,Y向的加速度均为2 m/s2的匀加速运动，在81～100 s恢复匀速直线运动，某传感器接收机采样周期为T=1 s，测量误差标准差为30 m，amax=9g,a-max=-9g，机动频率α的初始值设定为0.05。采用100次的蒙特卡洛仿真实验对改进后的算法与传统“当前”统计模型算法进行比较，选取跟踪飞行器的位置均方根误差(RMSE)作为评估指标。结果如图2、图3和表1所示。

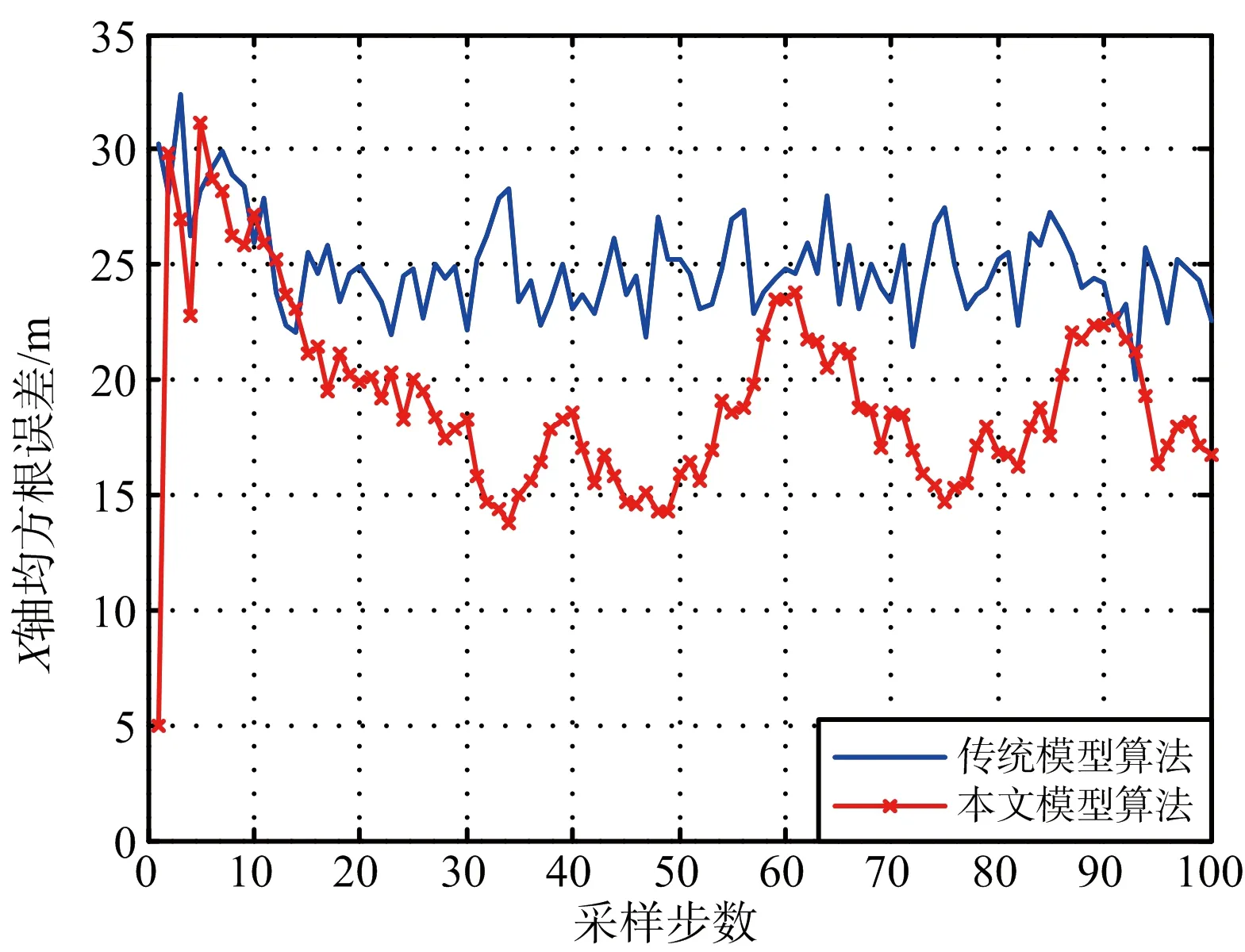
图2 X轴均方根误差曲线

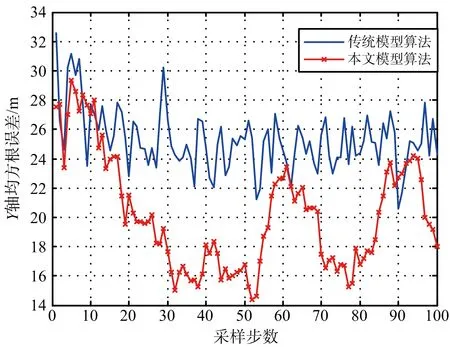
图3 Y轴均方根误差曲线

算法模型X轴RMSE/mY轴RMSE/m“CS”模型24.843725.2753改进“CS”模型19.124520.1935

从仿真结果可以看出，本文提出的改进算法能够进一步提高对目标的跟踪精度，尤其当目标作弱机动和非机动运动时，改善效果更加明显。

4 野值判别和剔除

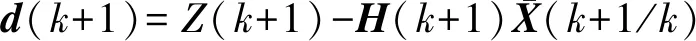
(15)

由于d(k+1)是均值为零的高斯随机量，其协方差矩阵为

E[d(k+1)dT(k+1)]=

H(k+1)P(k+1/k)HT(k+1)+R(k+1)

(16)

式中，P(k+1/k)表示预测误差协方差矩阵，R(k+1)为量测噪声协方差矩阵。

利用预测残差的上述统计性质可对Z(k+1)的每个分量进行判别，判别式为

|di(k+1)|≤

(17)

式中，下角i,i表示矩阵对角线上的第i个元素，di(k+1)表示d(k+1)的第i个分量，C为常数，可取3或4。如果上式成立，判别zi(k+1)为正确观测量，反之，判别zi(k+1)为野值，剔除该点测量值，并用预测值代替测量值[7]。实际试验过程中，虽然大部分航路是匀速直线运动，但总避免不了拐弯和上升下降等机动情况出现。这些机动情况下，容易导致滤波发散，为了避免发散引起的故障，如果连续剔除点数超过5个，则认为目标丢失，滤波重新开始，下一时刻到来时，对局部滤波器重新赋初值。

根据以上对野值点的判别和处理，结合试验实测数据，野值剔除效果如图4所示，由图可以看出，采用该算法能够有效地剔除野值点。

图4 野值点剔除效果比对

5 标准数据格式

惯导、一次雷达、二次雷达、遥测遥控和GPS等能够提供无人飞行器监控数据的平台和装备各不相同，它们的数据帧格式也不尽相同，在进入空管系统处理显示之前必须要将数据帧格式进行统一，规范其数据格式，经预处理过后的统一数据格式为：

struct TargetInfor

{

BYTE m_dataFrom; //数据来源

BYTE m_dataTo;

//数据发送目的地

BYTE m_dataType; //数据类型

unsigned short m_dataLength;

//数据长度

unsigned long m_Time; //时间

BYTE m_nTargetSN; //目标序号

double m_X,m_Y,m_Z; //X,Y,Z坐标

float m_A,m_E,m_D;

//方位角、高低角、斜距离

float m_fSpeed; //速度

BYTE m_nTraceStatus; //跟踪状态

};

6 结束语

本文提出了一种自适应Kalman滤波的无人飞行器监控数据预处理方法，通过对来自惯导、一次雷达、二次雷达、遥测遥控和GPS等无人飞行器监控数据进行预处理，使这些数据能够和空管系统进行兼容，并输入到空管系统进行处理显示，自动生成可视化信息，使雷达管制员席位能够及时准确显示无人航空器的高度、速度和位置，为飞行管制员提供准确的无人航空器监控平台，实现了对无人升空平台的雷达管制，经过测试对比，检验了所用技术方法的合理性和可行性。